Как решать дроби Ютуб

В статье покажем, как решать дроби на простых понятных примерах. Разберемся, что такое дробь и рассмотрим решение дробей!

Понятие дроби вводится в курс математики начиная с 6 класса средней школы.

Дроби имеют вид : ±X/Y, где Y — знаменатель, он сообщает на сколько частей разделили целое, а X — числитель, он сообщает, сколько таких частей взяли. Для наглядности возьмем пример с тортом:

В первом случае торт разрезали поровну и взяли одну половину, т.е. 1/2. Во втором случае торт разрезали на 7 частей, из которых взяли 4 части, т.е. 4/7.

Если часть от деления одного числа на другое не является целым числом, ее записывают в виде дроби.

Например, выражение 4:2 = 2 дает целое число, а вот 4:7 нацело не делится, поэтому такое выражение записывается в виде дроби 4/7.

Иными словами дробь — это выражение, которое обозначает деление двух чисел или выражений, и которое записывается с помощью дробной черты.

Как объяснить дроби? Что такое дробь? простое объяснение дробей. Как объяснить ребенку доли?

Если числитель меньше знаменателя — дробь является правильной, если наоборот — неправильной. В состав дроби может входить целое число.

Например, 5 целых 3/4.

Данная запись означает, что для того, чтобы получить целую 6 не хватает одной части от четырех.

Если вы хотите запомнить, как решать дроби за 6 класс, вам надо понять, что решение дробей, в основном, сводится к понимаю нескольких простых вещей.

• Дробь по сути это выражение доли. То есть числовое выражение того, какую часть составляет данное значение от одного целого. К примеру дробь 3/5 выражает, что, если мы поделили что то целое на 5 частей и количество долей или частей это этого целого — три.
• Дробь может быть меньше 1, например 1/2(или по сути половина), тогда она правильная. Если дробь больше 1, к примеру 3/2(три половины или один с половиной), то она неправильная и для упрощения решения, нам лучше выделить целую часть 3/2= 1 целая 1/2.
• Дроби это такие же числа, как 1, 3, 10, и даже 100, только числа это не целые а дробные. С ними можно выполнять все те же операции, что с числами. Считать дроби не сложнее, и далее на конкретных примерах мы это покажем.

Как решать дроби. Примеры.

К дробям применимы самые разные арифметические операции.

Приведение дроби к общему знаменателю

Например, необходимо сравнить дроби 3/4 и 4/5.

Чтобы решить задачу, сначала найдем наименьший общий знаменатель, т.е. наименьшее число, которое делится без остатка на каждый из знаменателей дробей

Наименьший общий знаменатель(4,5) = 20

Затем знаменатель обоих дробей приводится к наименьшему общему знаменателю

Ответ: 15/20 Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

пт., 2014-09-05 22:30 — lapsik

Должна признаться, что решать дроби — это мое самое любимое математическое действие. Это тема, которую я понимаю без вопросов. Можно сказать, хлебом не корми, дай только дроби порешать )))

вс., 2014-09-07 11:30 — булкин

Дроби я тоже люблю. Умножать и делить их — милое дело. Вообще мне кажется, что с решением дробей мало у кого могут быть проблемы, потому что все довольно просто. Есть в математике огромное количество гораздо более сложных вещей, чем дроби решать.

вс., 2016-04-10 17:23 — Гость (не зарегистрирован)

Я вообще не умею решать дроби, но понятие немного есть. И поэтому стараюсь как можно скорее научиться решать дроби как дважды два четыре. Мне легче с формулами сложные примеры решить чем решать дроби!

пн., 2021-12-13 13:38 — Гость

Для некоторых это нормально а для некоторых это просто ужасно математика отстой

ср., 2021-02-10 13:13 — Гость

говорит та самая красотка которая не навидит дроби

вс., 2014-09-07 22:59 — Ринат

Полезно бывает вспомнить то, что проходилось в школе когда-то и частично забыто. Да и я лично для себя несколько моментов новых открыл и очень рад. Правда появился еще вопрос по поводу того, изменилось ли что-то в данном случае или же нет? Потому что я не все помню и есть четкое мнение, что изменились уравнения уже.

пн., 2014-09-08 00:03 — Маринка

Всегда любила я дробить числа. А тут оказывается и вообще проще простого все это сделать можно, имея просто одно целое значение, которое не настолько и сложно просто поделить на частички, которые и будут нужны.

чт., 2015-08-13 08:06 — Funtik

Вроде бы все просто, а вот на примере с вычитанием 1/4 я расстерялся. Вот такие преобразования дроби для вычитания меня сбивают с толку.

чт., 2015-09-03 00:31 — Линейка

Так это еще слишком простые дроби здесь на примерах представлены. Я как заглянула в экзаменационные задания чуть не померла, сама такое не решу никогда.

пт., 2015-09-04 23:37 — Kross

Вы видео смотрели?! Мне лично очень понравилось, доступно, подробно, но кратко. Таким и должны быть математические видео-уроки.

вс., 2015-09-06 17:16 — Еврик

Согласен, видео хорошее, а вообще решение дробей не самое сложное в математике!

чт., 2019-08-08 17:13 — Юлия Кайбазакова Алексеевна 23 года (не зарегистрирован)

ну что поделаешь и помирать от этого не надо просто дроби надо решать и не коких проблем не будет
и все будет нормально

сб., 2015-10-03 21:14 — Алла (не зарегистрирован)

Вот честно говоря, если бы я не знала что такое дроби и как решить с ними примеры, посмотрев видео,я бы не поняла что к чему.
(Знаю что и как решать,просто хотела вспомнить)

пн., 2015-10-05 18:43 — admin

Что именно вы бы не поняли, Алла?

Источник: reshit.ru

Как решать дроби?

Узнай как решать дроби у нас на сайте. Сначала мы должны изучить сложение наших дробей с очень одинаковыми и неодинаковыми знаменателями. Тут всё просто. Нам необходимо складывать таким образом, чтобы наш знаменатель оставался на своем месте.

Если в нашей с вами конец нашей задачи, то нам необходимо приступать к выполнению нашей задачи, мы будем с вами решать ее пока не добьемся нужного нам результата. В этом случае целая часть выдвигается легко два делим на два равно единица.

Мы научимся с вами правильно складывать и решать наши дроби. Если мы с вами правильно начнем складывать наши дроби, то у нас не будет ошибок и задача наша будет выполнена. Но одинаковыми бывают они не всегда.

Также дроби встречаются везде, математика это очень важный предмет в нашей жизни и без него нам не обойтись. Математику не все понимаю особенно дроби это очень сложное вычитание и сложение между собой. Также в математике очень легко искать эти дроби они выглядят своеобразно.
В математики очень много сложений и вычитаний которые мы с вами должны решать. Также математика очень нужна при работе каким нибудь инженером, там нужно правильно все составлять без каких либо ошибок.
В математике очень нужно правильно все высчитывать иначе вы можете ошибиться и просчитаться.

Смотреть онлайн видео Как решать дроби:

Копирование информации с сайта greednews.su разрешено только при использовании активной гипер ссылки на новость, спасибо за то что цените наши авторские права!

Поделиться ссылкой:

Источник: greednews.su

Как решать алгебраические дроби? Теория и практика

Когда ученик переходит в старшую школу, математика разделяется на 2 предмета: алгебру и геометрию. Понятий становится все больше, задания все сложнее. У некоторых возникают трудности с восприятием дробей. Пропустили первый урок по этой теме, и вуаля. Как решать алгебраические дроби?

Вопрос, который будет мучить на протяжении всей школьной жизни.

Понятие алгебраической дроби

Начнем с определения. Под алгебраической дробью понимается выражения P/Q, где P является числителем, а Q – знаменателем. Под буквенной записью может скрываться число, числовое выражение, численно-буквенное выражение.

Прежде чем задаваться вопросом, как решать алгебраические дроби, для начала нужно понимать, что подобное выражение – часть целого.

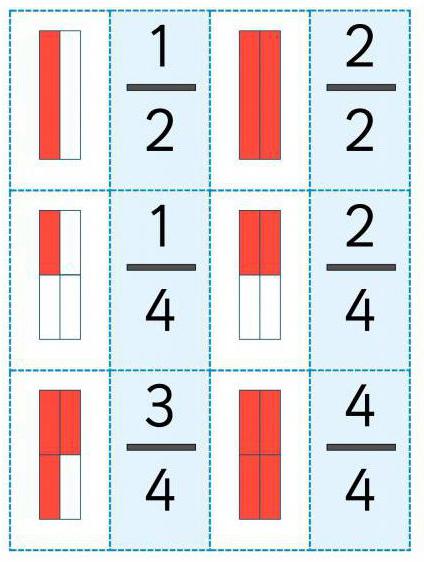
Как правило, целое – это 1. Число в знаменателе показывает, на сколько частей разделили единицу. Числитель необходим для того, чтобы узнать, сколько элементов взято. Дробная черта соответствует знаку деления. Допускается запись дробного выражения в качестве математической операции «Деление». В таком случае числитель – делимое, знаменатель – делитель.

Основное правило обыкновенных дробей

Когда учащиеся проходят данную тему в школе, им дают примеры на закрепление. Чтобы правильно их решать и находить различные пути из сложных ситуаций, нужно применять основное свойство дробей.

Оно звучит так: Если умножить и числитель, и знаменатель на одно и то же число или выражение (отличные от нуля), то значение обыкновенной дроби не изменится. Частным случаем от данного правила является разделение обеих частей выражения на одно и то же число или многочлен. Подобные преобразования называются тождественными равенствами.

Ниже будет рассмотрено, как решать сложение и вычитание алгебраических дробей, производить умножение, деление и сокращение дробей.

Математические операции с дробями

Рассмотрим, как решать, основное свойство алгебраической дроби, как применять его на практике. Если нужно перемножить две дроби, сложить их, разделить одну на другую или произвести вычитание, нужно всегда придерживаться правил.

Так, для операции сложения и вычитания следует найти дополнительный множитель, чтобы привести выражения к общему знаменателю. Если изначально дроби даны с одинаковыми выражениями Q, то нужно опустить этот пункт. Когда общий знаменатель найден, как решать алгебраические дроби? Нужно сложить или вычесть числители. Но!

Нужно помнить, что при наличии знака «–» перед дробью все знаки в числителе меняются на противоположные. Иногда не следует производить каких-либо подстановок и математических операций. Достаточно поменять знак перед дробью.

Часто используется такое понятие, как сокращение дробей. Это означает следующее: если числитель и знаменатель разделить на отличное от единицы выражение (одинаковое для обеих частей), то получается новая дробь. Делимое и делитель меньше прежних, но в силу основного правила дробей остаются равными изначальному примеру.

Целью этой операции является получение нового несократимого выражения. Решить данную задачу можно, если сократить числитель и знаменатель на наибольший общий делитель. Алгоритм операции состоит из двух пунктов:

1. Нахождение НОД для обеих частей дроби.
2. Деление числителя и знаменателя на найденное выражение и получение несократимой дроби, равной предшествующей.

Ниже показана таблица, в которой расписаны формулы. Для удобства ее можно распечатать и носить с собой в тетради. Однако, чтобы в будущем при решении контрольной или экзамена не возникло трудностей в вопросе, как решать алгебраические дроби, указанные формулы нужно выучить наизусть.

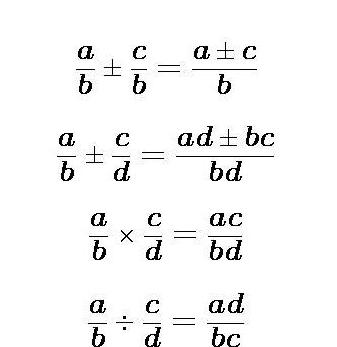
Несколько примеров с решениями

С теоретической точки зрения рассмотрен вопрос, как решать алгебраические дроби. Примеры, приведенные в статье, помогут лучше усвоить материал.

1. Преобразовать дроби и привести их к общему знаменателю.

2. Преобразовать дроби и привести их к общему знаменателю.

3. Сократить указанные выражения (с использованием изученного основного правила дроби и сокращения степеней)

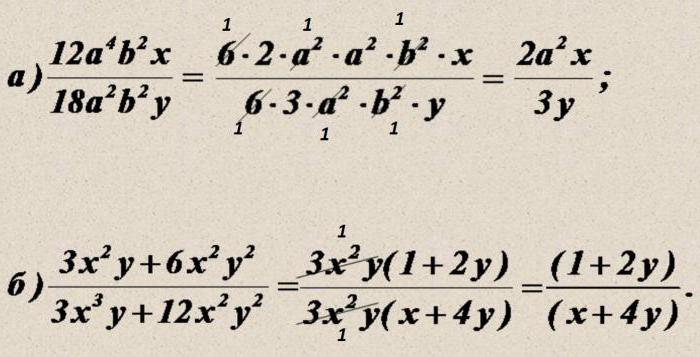
4. Сократить многочлены. Подсказка: нужно обнаружить формулы сокращенного умножения, привести к подобающему виду, сократить одинаковые элементы.

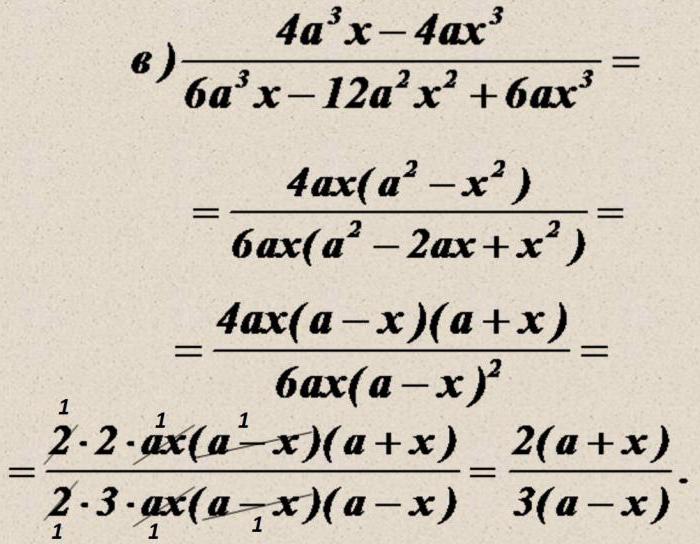
Задание на закрепление материала

1. Какие действия нужно произвести, что найти скрытое число? Решите примеры.

2. Умножьте и поделите дроби, пользуясь основным правилом.

После изучения теоретической части и расссмотрения практической вопросов больше возникнуть не должно.

Источник: fb.ru

Основные задачи и действия на обыкновенные дроби

Понять, что такое дробь, легко, если представить что-то целое, разделить его на равные части и взять какое-то количество частей. Для удобства и наглядных примеров вы всегда можете воспользоваться нашим онлайн калькулятором дробей. Предположим, у вас есть тортик. Вы его разрезали на 8 ровных, красивых кусочков.

1. Если вы берете один из восьми, для этого будет верно выражение . Где цифра 1 показывает, сколько кусочков вы взяли, а 8 показывает, на сколько кусков вы делили торт.
2. Если вы берете два кусочка из восьми, то записать это можно как 2/8. Где первая цифра показывает, что в этот раз вы взяли уже 2 кусочка, а вторая цифра показывает на сколько кусков вы поделили торт.
3. Если взять три кусочка из возьми, то записать это можно как 3/8.

Выражения, которые использовались для записи: 1/8, 2/8, 3/8 называются дробями (части чего-либо). Само слово «говорит само за себя» и означает дробление, деление, разделение.

Как устроена обыкновенная дробь

Обыкновенная дробь — это число вида «a/b», где «a» — это числитель, «b» — знаменатель. Оба значения — натуральные числа.

Числитель обыкновенной дроби (всегда стоит над чертой) — натуральное число, которое показывает, что мы делим. Это делимое.

Знаменатель обыкновенной дроби (всегда под чертой) — натуральное число, которое показывает, на сколько частей делим. Это делитель.

Черта дроби — символ деления чисел. Черта может быть горизонтальной:

или вертикальной: (a/b).

Равными обыкновенными называются дроби, между которыми можно поставить знак равенства. Так a/b и m/n можно назвать равными, если для них справедливо выражение: a × n = b × m.

Пример: выясним, равны ли: ½ и 3 ⁄6?

Для этого составим выражение и сравним: (1 × 6) и (2 × 3). Так как в обоих случаях результат равен 6, то 1 ⁄2 и 3 ⁄6 равны (являются равными).

Неравными обыкновенными называются дроби a ⁄b и m ⁄n, где a × n = b × m не является верным выражением.

Пример: выясним, равны ли 1 ⁄2 и 2 ⁄6?

Составляем выражение: (1 × 2) и (2 × 6). В первом случае результат равен 2, во втором 12. Так как 2≠12, то 1 ⁄2 и 2 ⁄6 неравны (являются неравными).

Как устроена десятичная дробь

Десятичная дробь — число, которое получается в результате деления числителя на знаменатель, где знаменатель равен 10, 100, 1000, 10000 и т.д.

Десятичная дробь отличается формой записи: вместо черты деления используется запятая, которая отделяет целую часть от дробной.

Примеры десятичных дробей:

• 0,6 (ноль целых шесть десятых);
• 2,01 (две целых одна сотая);
• 11,123 (одиннадцать целых сто двадцать три тысячных).

Десятичная дробь может быть конечной или бесконечной. Конечную от бесконечной отличает точно определенное количество цифр после запятой. У бесконечной – это количество не может быть определено, в большинстве случаев их округляют от 1 до 3х знаков после запятой в знаменателе.

Представление целого числа в виде дроби

Любое целое число может быть представлено в виде дроби. Для этого в качестве знаменателя нужно указывать 1 и дробь будет иметь вид:

Например, 4 должно быть представлено в виде дроби. Для этого под черту деления нужно записать: 4/1

Любое целое число можно представить в виде дроби с любым знаменателем. Предположим, b нужно представить в виде дробного выражения со знаменателем a. Под черту деления указываем нужное значение (a), а в числитель a × b. Результат будет выглядеть так:

Сокращение дробей

Чтобы сократить дробь, необходимо разделить числитель и знаменатель на одно и тоже натуральное число.

Простым языком, сократить значит сделать короче и проще для восприятия.

Пример: если сравнивать дроби 1/2 и 24/48, то визуально первая кажется намного проще и легче, хотя является сокращенной версией второй.

Правило сокращения дробью: числитель и знаменатель делят на одно и тоже число, рядом записывают полученные значения. Делить можно последовательно, пока итоговая версия не будет выглядеть простой и понятной.

Сравнение дробей

Чтобы сравнивать дроби, нужно заполнить несколько правил:

1. Если знаменатели у дробей одинаковые, то больше та, где числитель больше. Например, требуется сравнить: ⅞ и ⅝. Так как у них одинаковый делитель (8), то сравнить нужно делимое. Числитель первой дроби больше (7 >5), следовательно и 7/8 > 5/8.
2. Если числители у дробей одинаковые, то больше та дробь, где знаменатель меньше. Например, требуется сравнить: 8/11 и 8/9. Так как у дробей одинаковые числители (8), то сравнить нужно знаменатели. Знаменатель второй дроби меньше (9 < 11), следовательно и 8/11 < 8/9.
3. Если у дробей разные и числители, и знаменатели, то первоочередное их приводят к общему знаменателю, а потом сравнивают, применяя правило сравнения дробей с общим знаменателем из п.1. Например, требуется сравнить: 1/6 и 2/7. Решение: приводим дроби к общему знаменателю: 42. Сравниваем 7/42 и 12/42. По правилу сравнения, больше та дробь, чей числитель больше: 7/42 по правилу сложения дробей с одинаковым знаменателем.

Для наглядности решение представлено на картинке пошагово:

Вычитание дробей с одинаковыми знаменателями

Чтобы вычесть дробь с одинаковым знаменателем: из числителя одной дроби вычтите числитель второй, знаменатель оставить тот же: a/b — c/b = (a-c)/b.

При необходимости можно выделить целую часть или сократить выражение.

Вычитание дробей с разными знаменателями

Чтобы выполнить вычитание, необходимо последовательно выполнять алгоритм.

Как вычесть дроби с разным знаменателем:

1. Найти наименьшее общее кратное. Чтобы найти наименьшее кратное нужно выписать все числа, которые в сумме дают значения знаменателях и перемножить их.
2. Найти дополнительные множители: наименьшее общее кратное разделить на каждый знаменатель. Полученные числа записать сверху над числителем. Так нагляднее.
3. Применить основное свойство дробей: перемножим числитель и знаменатель на дополнительный множитель. После умножения значение под чертой равно наименьшему общему кратному (пункт 1).
4. Вычитаем дробные выражения, используя правило вычитания дробей с одинаковым знаменателем.

Для наглядности решение представлено на картинке пошагово:

Умножение дроби на число

Чтобы умножить дробь a/b на с необходимо поочередно умножить числитель и знаменатель на с. То есть: a/b × с = (a × с)/(b ×с)

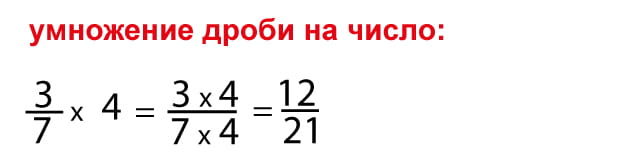
Умножение дробей

Чтобы умножить дроби, нужно перемножить значения под чертой и над чертой соответственно.

Если более корректно, то правило звучит так: произведение дробей равно дроби, числитель которой равен произведению числителями, а знаменатель — произведению знаменателей.

Деление дробей

Чтобы разделить дроби, нужно запомнить следующую последовательность действий:

1. Числитель первой умножить на знаменатель второй, результат умножения записать в числитель;
2. Знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель.

Если использовать более подход, то правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить первую на обратную от второй: a/b ÷ n/m= (a × m)/(b × n).

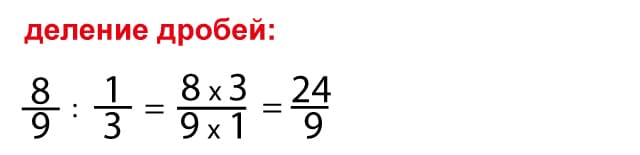
Деление дроби на число

Чтобы разделить дробь на число, выполните следующее:

1. Представьте число в виде дроби, «переверните её» (поменяйте местами делитель и делимое).
2. Умножить первую дробь на новую по правилу умножения.

Правило звучит так: дробь умножается на число, обратное второму:
a/b ÷ с=(a)/b × (1)/c = (a × 1)/(b × с)

Деление числа на дробь

Чтобы разделить число на дробь, выполните следующее:

1. «Переверните» дробь — поменяйте местами числитель и знаменатель.
2. Умножаем число и дробь по правилу умножения

Правило звучит так: число умножается на дробь, обратную данной:
с ÷ a/b =с × b/a = (с × b)/a

Пример: 18 ÷ 1/3 = 18 × 3/1 = 54/1 = 54

Как решать дробями. Примеры

В данном разделе представлены основные примеры сложения, вычитания, деления и умножения дробями.

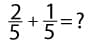
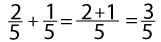
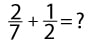
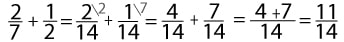
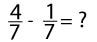
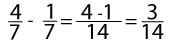
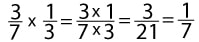
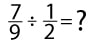
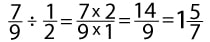
Задания и примеры для самостоятельного решения

В данном разделе мы подготовили интересные задания, которые помогут закрепить пройденный материал:

1. Найдите ошибку в решении:

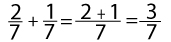
Ответ: согласно правилу сложения дробей с одинаковым знаменателем, складывать необходимо только числа над чертой. Верное решение:

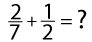
2. Найдите значение выражения:

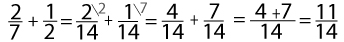
Ответ:

3. Поставьте знак между 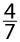и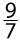

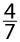
Ответ:

Источник: web-calculator.ru