Удар представляет собой механическое явление, при котором кратковременное взаимодействие тел вызывает конечное изменение вектора скорости всех или некоторых точек материальной системы при ничтожно малом изменении положения точек системы. Интервал времени, в течение которого происходит удар, обозначается буквой и называется временем удара.
Удар представляет собой распространенное явление при рассмотрении движения как макроскопических тел, так и микроскопических частиц, например молекул газа. Таким образом, явление удара играет существенную роль в ряде технических и физических задач. Природа удара существенно зависит от физической структуры соударяющихся тел.
Мгновенные силы
Так как время, в течение которого происходит удар, мало, то конечному изменению скорости при ударе соответствуют весьма большие ускорения точек системы. Поэтому силы, действующие в процессе удара, во много раз превышают обычные силы.
Эти силы называются мгновенными силами. Непосредственное измерение мгновенных сил весьма затруднено, так как время удара обычно выражается в тысячных или десятитысячных долях секунды. Кроме того, в течение этого крайне малого промежутка времени мгновенные силы не остаются постоянными: они увеличиваются от нуля до некоторого максимума, а затем снова уменьшаются до нуля. Благодаря этому силы, вызывающие удар, приходится характеризовать при помощи некоторых специальных понятий.
Физика — импульс силы
Ударный импульс
Рассмотрим точку массы движущуюся под действием некоторой конечной силы Пусть затем в момент к ней прикладывается мгновенная сила Р, действие которой прекращается в момент . Обозначим скорости точки в моменты и соответственно , применяя к этим моментам теорему импульсов, получим:
Первый из этих интегралов представляет импульс конечной силы за время и потому является малой величиной того же порядка, что и . Следовательно, скорость рассматриваемой точки может получить конечное изменение лишь в том случае, если будет конечным импульс мгновенной силы Р, обозначая который через имеем:
где называется ударным, или мгновенным, импульсом, он характеризует действие мгновенной силы при ударе.
Основное уравнение теории удара
Так как импульс конечной силы имеет порядок малой величины то им можно пренебречь по сравнению с конечным импульсом Следовательно, при изучении действия мгновенных сил во время удара можно не учитывать действия конечных сил, и теорема импульсов для точки при ударе имеет вид:
Скорости точки, соответствующие началу и концу удара, носят название до ударной и после ударной скорости. Полученное равенство, связывающее скорости точки до и после удара с мгновенным импульсом, называется основным уравнением теории удара. Оно в этой теории играет роль основного закона динамики.
Смещение точек при ударе
Скорость точки в процессе удара остается конечной, изменяясь от до Отсюда перемещение точки будет или это будет малая величина порядка т. Таким образом, за время удара точка не успевает сместиться сколько-нибудь заметным образом. Пренебрегая этим ничтожно малым перемещением, можно сказать, что единственным следствием действия мгновенной силы является внезапное изменение скорости точки. Так как вектор скорости может при этом изменяться не только по величине, но и по направлению, то траектория точки в момент удара может получить излом (на траектории образуется угловая точка) (рис. 131).
Физика ОГЭ — Считаем силу удара барион Наруто
Уравнения удара материальной системы
Рассмотрим механическую систему, состоящую из материальных точек. Пусть среди внешних и внутренних сил, действующих на точки системы, будут мгновенные силы, которые обозначим соответственно Тогда для каждой точки системы можно записать основное уравнение удара:
Умножим каждое из этих равенств на r, векторно, где — радиус-вектор точки, соответствующий моменту удара (или бесконечно малому интервалу времени удара). Тогда получим равенство:
Чтобы исключить внутренние мгновенные силы действующие на систему, сложим почленно каждую группу указанных равенств. В результате получим:
так как ранее доказывалось, что для внутренних сил
где Р — количество движения системы.
где ударный импульс внешней силы, действующей на точку системы. Следовательно, первое из полученных равенств можно записать в виде:
Так как будут количеством движения системы до и после удара, то имеем: изменение количества движения системы за время удцра равно сумме мгновенных импульсов всех внешних сил, действующих на систему.
Если последнее равенство переписать в виде:
где соответственно скорости центра инерции системы до и после удара, то имеем: изменение скорости центра инерции за время удара равно сумме всех внешних ударных импульсов, разделенной на массу системы. Наконец, так как
где — кинетический момент системы, то имеем:
где — кинетические моменты системы до и после удара. В свою очередь
где — момент внешнего ударного импульса, действующего на точку.
или изменение кинетического момента за время удара равно сумме моментов всех внешних ударных импульсов. Уравнения (19.1) или и (19.2) представляют собой основные уравнения удара механической системы, заменяющие собой теоремы о количестве движения и кинетическом моменте, которые применяются при изучении движения системы, находящейся под действием обычных (конечных) сил.
Источник: scask.ru
§ 15. Удар абсолютно упругих и неупругих тел
Примером применения законов сохранения импульса и энергии при решении реальной физической задачи является удар абсолютно упругих и неупругих тел.
Удар (или соударение)—это столкновение двух или более тел, при котором взаимодействие длится очень короткое время. Помимо ударов в прямом смысле этого слова (столкновения атомов или биллиардных шаров) сюда можно отнести и такие, как удар человека о землю при прыжке с трамвая и т. д. Силы взаимодействия между сталкивающимися телами (ударные или мгновенные силы) столь велики, что внешними силами, действующими на них, можно пренебречь. Это позволяет систему тел в процессе их соударения приближенно рассматривать как замкнутую систему и применять к ней законы сохранения.
Тела во время удара претерпевают деформацию. Сущность удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара имеет место перераспределение энергии между соударяющимися телами. Наблюдения показывают, что относительная скорость тел после удара не достигает своего прежнего значения. Это объясняется тем, что нет идеально упругих тел и идеально гладких поверхностей. Отношение нормальных составляющих относительной скорости тел после и да удара называется коэффициентом восстановления :
Прямая, проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения, называется линией удара. Удар называется центральным, если тела до удара движутся вдоль прямой, проходящей через их центры масс. Мы будем рассматривать только центральные абсолютно упругие и абсолютно неупругие удары.
Абсолютно упругий удар — столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию (подчеркнем, что это идеализированный случай).
Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения кинетической энергии.
Обозначим скорости шаров массами т1 и m2 до удара через v1 и v2, после удара—через 
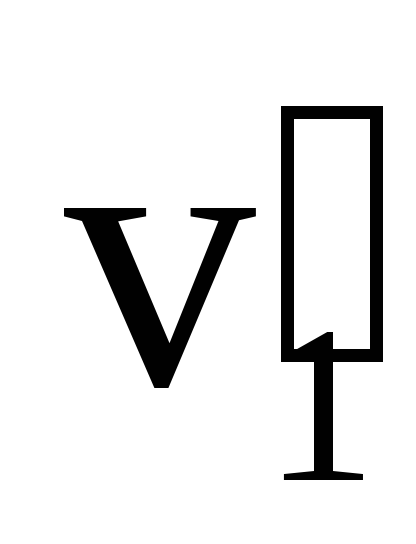и 
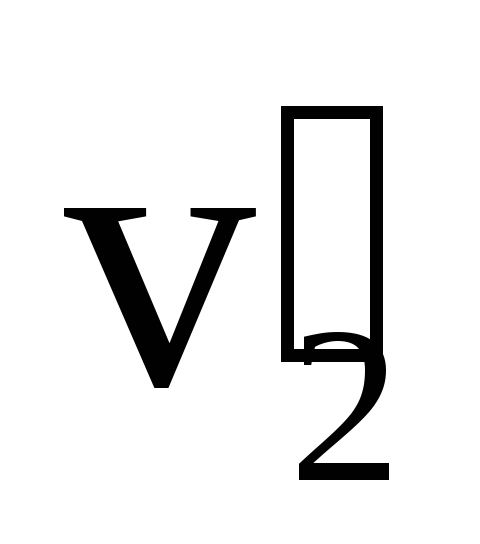(рис. 18). В случае прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, соединяющей их центры. Проекции векторов скорости на эту линию равны модулям скоростей. Их направления учтем знаками: положительное значение припишем движению вправо, отрицатель-нос — движению влево.
При указанных допущениях законы сохранения имеют вид
(15.1)
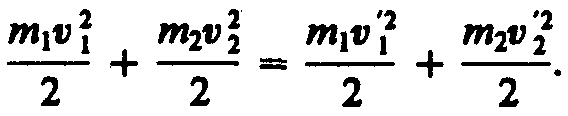
(15.2)
Произведя соответствующие преобразования в выражениях (15.1) и (15.2), получим
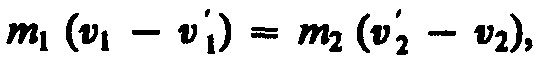
(15.3)
(15.4)
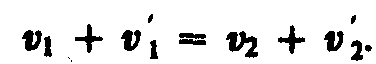
(15.5)
Решая уравнения (15.3) и (15.5), находим
(15.6)
(15.7)
Разберем несколько примеров.
(15.8)
(15.9)
Проанализируем выражения (15.8) в (15.9) для двух шаров различных масс:
а) т1=т2. Если второй шар до удара висел неподвижно (v2=0) (рис. 19), то после удара остановится первый шар (
=0), а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался первый шар до удара (
);
б) т1>т2. Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью (
1). Скорость второго шара после удара больше, чем скорость первого после удара (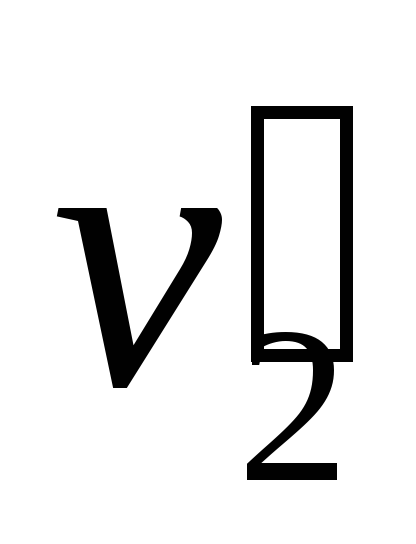
>
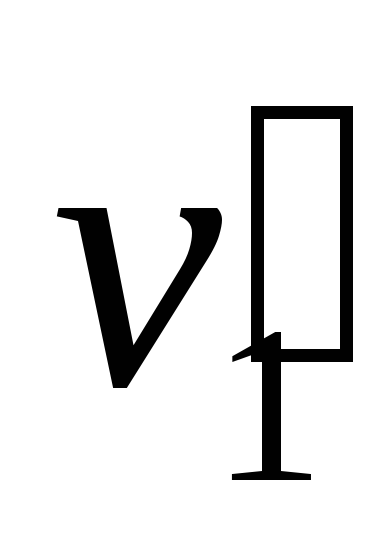) (рис. 20);
в) т1т2. Направление движения первого шара при ударе изменяется—шар отскакивает обратно. Второй шар движется в ту же сторону, в которую двигался первый шар до удара, но с меньшей скоростью, т. е. 1 (рис. 21);
г) т2>>т1 (например, столкновение шара со стеной). Из уравнений (15.8) и (15.9) следует, что 
= –v1, 
2m1v1/m20.
2. При т1=т2 выражения (15.6) и (15.7) будут иметь вид
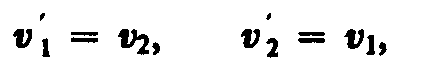
т. е. шары равной массы «обмениваются» скоростями.
Абсолютно неупругий удар — столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. Продемонстрировать абсолютно неупругий удар можно с помощью шаров из пластилина (глины), движущихся навстречу друг другу (рис. 22).
Если массы шаров т1 и т2, их скорости до удара v1 и v2, то, используя закон сохранения импульса, можно записать
где v — скорость движения шаров после удара. Тогда
(15.10)
Если шары движутся навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий большим импульсом. В частном случае, если массы шаров равны (т1=т2), то
Выясним, как изменяется кинетическая энергия шаров при центральном абсолютно неупругом ударе. Так как в процессе соударения шаров между ними действуют силы, зависящие не от самих деформаций, а от их скоростей, то мы имеем дело с силами, подобными силам трения, поэтому закон сохранения механической энергии не должен соблюдаться. Вследствие деформации происходит «потеря» кинетической энергии, перешедшей в тепловую или другие формы энергии. Эту «потерю» можно определить по разности кинетической энергии тел до и после удара:
Используя (15.10), получаем
Если ударяемое тело было первоначально неподвижно (v2=0), то
Когда m2>>m1 (масса неподвижного тела очень большая), то vv1 и почти вся кинетическая энергия тела при ударе переходит в другие формы энергии. Поэтому, например, для получения значительной деформации наковальня должна быть массивнее молотка. Наоборот, при забивании гвоздей в стену масса молотка должна быть гораздо большей (m1>>m2), тогда vv1 и практически вся энергия затрачивается на возможно большее перемещение гвоздя, а не на остаточную деформацию стены.
Абсолютно неупругий удар — пример того, как происходит «потеря» механической энергии под действием диссипативных сил.
3.1. Определить: 1) работу поднятия груза по наклонной плоскости; 2) среднюю и 3) максимальную мощности подъемного устройства, если масса груза 10 кг, длина наклонной плоскости 2 м, угол ее наклона к горизонту 45°, коэффициент трения 0,1 и время подъема 2 с. [1) 173 Дж; 2) 86 Вт; 3) 173 Вт]
3.2. С башни высотой 35 м горизонтально брошен камень массой 0,3 кг. Пренебрегая сопротивлением воздуха, определить: 1) скорость, с которой брошен камень, если через 1 с после начала движения его кинетическая энергия 60 Дж: 2) потенциальную энергию камня через 1 с после начала движения. [1) 17,4 м/с; 2) 88,6 Дж]
3.3. Пренебрегая трением, определить наименьшую высоту, с которой должна скатываться тележка с человеком по желобу, переходящему в петлю радиусом 10 м, чтобы она сделала полную петлю и не выпала из желоба. [25 м]
3.4. Пуля массой m=10 г, летевшая горизонтально со скоростью v=500 м/с, попадает в баллистический маятник длиной l=1 м и массой M=5 кг и застревает в нем. Определить угол отклонения маятника. [18°30′]
3.5. Зависимость потенциальной энергии частицы в центральном силовом поле от расстояния r до центра поля задается выражением П (r) = , где А и В — положительные постоянные. Определить значение r0, соответствующее равновесному положению частицы. Является ли это положение положением устойчивого равновесия? [r0=2A/B]
3.6. При центральном абсолютно упругом ударе движущееся тело массой т1 ударяется о покоящееся тело массой m2, в результате чего скорость первого тела уменьшается в n=1,5 раза. Определить: 1) отношение m1/m2; 2) кинетическую энергию Т2 второго тела, если первоначальная кинетическая энергия первого тела T1=1000 Дж. [1) 5; 2) 555 Дж]
3.7. Тело массой т1=4 кг движется со скоростью v1=3 м/с и ударяется о неподвижное тело такой же массы. Считая удар центральным и неупругим, определить количество теплоты, выделившееся при ударе. [9 Дж]
Источник: studfile.net
Упругое соударение
Соударение — это столкновение двух тел. При соприкосновении тела обмениваются энергией и импульсом. После соударения они двигаются со скоростями, которые отличаются по направлению и величине от их скоростей до столкновения.
При лобовом центральном соударении центры масс обоих тел двигаются вдоль одной линии. Силы взаимодействия, возникающие при соударении, параллельны направлению движения. Если применить к такой системе двух тел закон сохранения импульса, то полный импульс системы будет равен алгебраической сумме импульсов обоих тел.
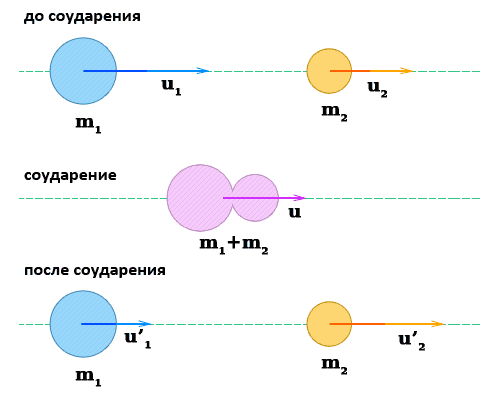
Упругое соударение
При упругом соударении на протяжении кратковременного соприкосновения тела двигаются с общей скоростью, затем они разлетаются и продолжают двигаться с разными скоростями.
| масса первого тела, | кг |
| масса второго тела, | кг |
| скорость первого тела до соударения, | метр/секунда |
| масса второго тела до соударения, | метр/секунда |
| скорость первого тела после соударения, | метр/секунда |
| масса второго тела после соударения, | метр/секунда |
то из закона сохранения импульса следует
[ m_1 u_1 + m_2 u_2 = m_1 u`_1 + m_2 u`_2 ]
[ m_1 (u_1 — u`_1) = m_2 (u`_2 — u_2) ]
Из закона сохранения энергии получаем
[ frac + frac = frac + frac ]
[ m_1 (u_1 ^2 — u`_1 ^2) = m_2 (u`_2 ^2 — u_2 ^2) ]
подставив формулу разность квадратов получим
[ m_1 (u_1 — u`_1)(u_1 + u`_1) = m_2 (u`_2 — u_2)(u`_2 + u_2) ]
воспользовавшись законом сохранения импульса, находим
[ u_1 + u`_1 = u`_2 + u_2 ]
Сумма скоростей до и после соударения одинакова при любом соударении тел.
Из формулы (6) следует
[ u`_2 = u`_1 + u_1 — u_2 ]
[ u`_1 = u`_2 + u_2 — u_1 ]
Подставив эти выражения в видоизмененный закон сохранения импульса, получим
[ m_1 (u_1 — u`_1) = m_2 (u`_1 + u_1 — u_2 — u`_2) ]
[ m_1 (u_1 — u_2 — u`_2 + u_1) = m_2 (u`_2 — u_2) ]
откуда, разрешив относительно u`1 и u`2 найдем
При противоположном направлении; движения скорость считается отрицательной.
Поскольку полная энергия до и после соударения остается неизменной, после столкновения тела приобретают свою первоначальную форму, возникающие в момент соударения деформации исчезают.
Источник: www.fxyz.ru
Удар (примеры формула)
Что такое удар Взаимодействие тел путем соударения
Это взаимодействие тел, при котором за очень малый промежуток времени (тысячные доли секунды) происходят значительные изменения скоростей этих тел, называется соударением или ударом. Такая форма взаимодействия тел весьма распространена в природе, особенно в микромире.
Например, путем соударения взаимодействуют атомы и молекулы в тепловом движении, путем соударения осуществляется взаимодействие быстро движущихся электронов или фотонов с частицами вещества, взаимодействие ядер атомов и элементарных частиц при ядерных реакциях и т. д.
Различают соударение упругое, при котором кинетическая энергия частиц остается неизменной, только перераспределяется между ними, и неупругое, при котором кинетическая энергия частиц уменьшается: часть ее переходит в другие виды энергии.
Ограничимся рассмотрением простейшего случая — соударения двух шаров из одинакового вещества, так как оно является наиболее характерным для рассматриваемых явлений.
Вследствие исключительной кратковременности взаимодействия в телах возникают столь значительные внутренние силы, что внешними силами, действующими на них, можно пренебречь и, считая систему замкнутой, применить к ней закон сохранения количества движения.
Центральный удар
Рассмотрим вначале наиболее простой — центральный удар, т. е. соударение двух шаров А и Б (рис. 2, а), центры масс которых двигаются по одной прямой RS в одинаковом направлении. Массы шаров m1 и m2, скорости υ1 и υ2 и количества движения m1υ1 и m2υ2. Допустим, что υ1> υ2, тогда через некоторое время шар А догонит Б произойдет соударение. Вследствие инерции скорость шара Б не может мгновенно изменяться и потому шар А оказывает на шар Б давление, вызывающее деформацию сжатия соприкасающихся частей обоих шаров.
При этом шар А замед ляется, а шар Б ускоряется. Когда скорости шаров сравняются, дальней шая деформация их прекращается. Это — первая фаза удара: сближение и деформация. Если пренебречь потерей энергии при деформации, то общую скорость шаров υ0 можно определить, пользуясь законом сохранения количества движения:
Проверь хорошо ли Вы знаете науки
Ты получил <> снаружи >
Если соударение неупругое, то деформация шаров является остаточной и удар заканчивается первой фазой: шары продолжают двигаться вместе с некоторой скоростью, значительно меньшей, чем скорость υ0, вследствие потери части кинетической энергии при необратимой деформации.
При упругом ударе вслед за первой наступает вторая фаза (восстановление формы и перераспределение скоростей): за счет упругости шары принимают прежнюю форму и при этом взаимно отталкиваются. Вследствие этого скорость шара А еще больше уменьшается, а скорость шара Б увеличивается и шары расходятся, имея скорости υ1‘ и υ2‘ иные, чем до удара (рис. 2,б). Эти скорости зависят от скоростей, которые шары имели до удара, и от соотношения масс шаров.
Соударение шаров при одинаковой массе
Рассмотрим некоторые частные случаи. Если массы шаров равны, то после удара шары начинают двигаться, обменявшись скоростями (рис. 3, а). Если до удара второй шар был неподвижным, то после удара первый шар останавливается, а второй начинает двигаться со скоростью, которую имел первый шар (рис. 3, б).
В случае когда масса движущегося шара больше, чем у неподвижного, после удара оба шара будут двигаться в одном направлении с разными скоростями подобно случаю, изображен ному на рис. 2. б.
Если масса движущегося шара меньше, чем у неподвиж ного, то при ударе шар с меньшей массой оттолкнется от большого шара и будет двигаться в обратном направлении. Шар с большой массой начинает двигаться в направлении удара (рис. 3, в).
Рассмотрим центральный удар шара о неподвижную упругую стенку (рис. 3, г). Механизм удара аналогичен удару двух шаров. Скорость шара при этом, не изменяя величины, меняет знак на обратный: υ = — υ.
Вычислим импульс i’ силы, действующий на шар со стороны стенки. Он равен изменению количества движения шара:
i’= mυ‘ — mυ = — mυ — mυ = — 2mυ.
Следовательно, по третьему закону Ньютона, на стенку со стороны шара действует импульс i = —i’ =2mυ.
Удар шаров под углом
Удар может произойти также и между шарами, направления движения которых составляют некоторый угол, или в том случае, когда центры масс шаров, двигающихся в одном и том же направлении, не лежат на одной прямой. Подобный удар называется нецентральным или боковым.
Рассмотрим наиболее простой случай бокового удара двигающегося шара о второй — неподвижный. Разложим скорость v первого шара на две составляющие: υr направленную по прямой, соединяющей центры шаров, и υt направленную перпендикулярно этой прямой (рис 4). При ударе может изменяться только составляющая скорости υr так как только в этом направлении действуют упругие силы деформации шаров.
Если массы шаров равны, то двигающийся шар передаст составляющую скорости υr неподвижному шару. Следовательно, после удара второй шар двигается со скоростью υr а первый шар — со скоростью υt. Угол между направлениями шаров будет прямым.
При не равной массе
Когда массы шаров не равны, то составляющая скорости υr будет перераспределяться между ними. При этом второй шар во всех случаях двигается со скоростью υr‘, совпадающей по направлению, но меньшей по величине, чем скорость υr. Первый шар двигается по направлению, несколько отклоняющемуся от направления скорости υt.
Если масса первого шара больше то отклонение происходит в сторону второго шара и угол между направлениями движения шаров будет острым. Если масса первого шара меньше, то отклонение происходит в противоположную сторону и угол между направлениями движения шаров будет тупым .
Таким образом, по характеру образующейся после удара вилки можно судить о соотношении масс соударявшихся шаров.
Выделенная энергия
При упругом ударе между шарами или между микрочастицами происходит перераспределение их кинетической энергии. При равных массах шар или микрочастица с более высокой энергией передает часть своей энергии шару или микрочастице с меньшей энергией.
При неупругом ударе шаров часть их кинетической энергии превращается в теплоту, выделяющуюся при остаточной деформации. При неупругом соударении микрочастиц часть кинетической энергии может затрачиваться на изменение их внутренней структуры, т. е. превращаться в потенциальную энергию, может переходить в энергию электромагнитного излучения и т. п.
Статья на тему удар
Похожие страницы:
Содержание статьи1 Основные представления кинетической теории газов1.1 Кто открыл закон закон распределения молекул1.2 Пример определения Основные представления кинетической теории газов Мгновенные.
Содержание статьи1 Что такое работа и энергия Закон сохранения и превращения энергии1.1 Превращение форм материи1.2 Кинетическая и потенциальная энергия1.3 Чем.
Кинетическая теория газов В настоящее время закон Авогадро может быть выведен теоретически из так называемой кинетической теории газов. Не приводя.
Содержание статьи1 Что такое теплота Первое начало термодинамики1.1 Изменение внутренней энергии1.2 Пример работы теплоты Что такое теплота Первое начало термодинамики Это.
Содержание статьи1 ЧТО ТАКОЕ КИНЕТИЧЕСКАЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ1.1 Определение потенциальной энергии1.2 Кинетическая энергия1.3 Кинетическая энергия формула1.4 Что такое удар или.
Звук это механическое явление, субъективно воспринимаемое специальным органом чувств человека и животных. Этот термин часто употребляется в более широком смысле.
Понравилась статья поделись ей
Leave a Comment
Для отправки комментария вам необходимо авторизоваться.
Источник: znaesh-kak.com