Закон сохранения импульса лодка расстояние

При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой .

В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

Этот фундаментальный закон природы называется законом сохранения импульса . Он является следствием из второго и третьего законов Ньютона.

Рассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим через и По третьему закону Ньютона Если эти тела взаимодействуют в течение времени , то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны: Применим к этим телам второй закон Ньютона:
где и – импульсы тел в начальный момент времени, и – импульсы тел в конце взаимодействия. Из этих соотношений следует:

Границы применимости закона сохранения импульса | Физика ЕГЭ

Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, т. е. векторную сумму импульсов всех тел, входящих в эту систему.

Рис. 1.17.1 иллюстрирует закон сохранения импульса на примере нецентрального соударения двух шаров разных масс, один из которых до соударения находился в состоянии покоя.

Нецентральное соударение шаров разных масс: 1 – импульсы до соударения; 2 – импульсы после соударения; 3 – диаграмма импульсов

Изображенные на рис. 1.17.1 вектора импульсов шаров до и после соударения можно спроектировать на координатные оси и . Закон сохранения импульса выполняется и для проекций векторов на каждую ось. В частности, из диаграммы импульсов (рис. 1.17.1) следует, что проекции векторов и импульсов обоих шаров после соударения на ось должны быть одинаковы по модулю и иметь разные знаки, чтобы их сумма равнялась нулю.

Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение .

При стрельбе из орудия возникает отдача – снаряд движется вперед, а орудие – откатывается назад. Снаряд и орудие – два взаимодействующих тела. Скорость, которую приобретает орудие при отдаче, зависит только от скорости снаряда и отношения масс (рис. 1.17.2). Если скорости орудия и снаряда обозначить через и а их массы через и , то на основании закона сохранения импульса можно записать в проекциях на ось

Отдача при выстреле из орудия

На принципе отдачи основано реактивное движение . В ракете при сгорании топлива газы, нагретые до высокой температуры, выбрасываются из сопла с большой скоростью относительно ракеты. Обозначим массу выброшенных газов через , а массу ракеты после истечения газов через . Тогда для замкнутой системы «ракета + газы» на основании закона сохранения импульса (по аналогии с задачей о выстреле из орудия) можно записать:

закон сохранения импульса. #физика #анимация #егэ #лодка

где – скорость ракеты после истечения газов. В данном случае предполагается, что начальная скорость ракеты равнялась нулю.

Полученная формула для скорости ракеты справедлива лишь при условии, что вся масса сгоревшего топлива выбрасывается из ракеты одновременно . На самом деле истечение происходит постепенно в течение всего времени ускоренного движения ракеты. Каждая последующая порция газа выбрасывается из ракеты, которая уже приобрела некоторую скорость.

Для получения точной формулы процесс истечения газа из сопла ракеты нужно рассмотреть более детально. Пусть ракета в момент времени имеет массу и движется со скоростью (рис. 1.17.3 (1)). В течение малого промежутка времени из ракеты будет выброшена некоторая порция газа с относительной скоростью Ракета в момент будет иметь скорость а ее масса станет равной , где (рис. 1.17.3 (2)).

Масса выброшенных газов будет, очевидно, равна . Скорость газов в инерциальной системе будет равна Применим закон сохранения импульса. В момент времени импульс ракеты равен а импульс испущенных газов равен В момент времени импульс всей системы был равен Предполагая систему «ракета + газы» замкнутой, можно записать:

Величиной можно пренебречь, так как . Разделив обе части последнего соотношения на и перейдя к пределу при , получим

. Масса ракеты , ее скорость 2 – Ракета в момент времени . Масса ракеты , где , ее скорость масса выброшенных газов , относительная скорость газов скорость газов в инерциальной системе

Величина есть расход топлива в единицу времени. Величина называется реактивной силой тяги Реактивная сила тяги действует на ракету со стороны истекающих газов, она направлена в сторону, противоположную относительной скорости. Соотношение
выражает второй закон Ньютона для тела переменной массы. Если газы выбрасываются из сопла ракеты строго назад (рис. 1.17.3), то в скалярной форме это соотношение принимает вид:

,

где – модуль относительной скорости. С помощью математической операции интегрирования из этого соотношения можно получить формулу для конечной скорости ракеты:
где – отношение начальной и конечной масс ракеты. Эта формула называется формулой Циолковского . Из нее следует, что конечная скорость ракеты может превышать относительную скорость истечения газов. Следовательно, ракета может быть разогнана до больших скоростей, необходимых для космических полетов. Но это может быть достигнуто только путем расхода значительной массы топлива, составляющей большую долю первоначальной массы ракеты. Например, для достижения первой космической скорости при (скорости истечения газов при сгорании топлива бывают порядка ) стартовая масса одноступенчатой ракеты должна примерно в превышать конечную массу. Для достижения конечной скорости отношение должно быть равно .

Модель. Реактивное движение

Значительное снижение стартовой массы ракеты может быть достигнуто при использовании многоступенчатых ракет , когда ступени ракеты отделяются по мере выгорания топлива. Из процесса последующего разгона ракеты исключаются массы контейнеров, в которых находилось топливо, отработавшие двигатели, системы управления и т. д. Именно по пути создания экономичных многоступенчатых ракет развивается современное ракетостроение.

Источник: physics.ru

Закон cохранения импульса

Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.

Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.

Закон сохранения импульса

В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:

А выглядит — вот так:

Простая задачка

Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?

Решение:

Запишем закон сохранения импульса для данного процесса.

p0 — это импульс системы мальчик + лодка до того, как мальчик спрыгнул,

p1 — это импульс мальчика после прыжка,

p2 — это импульс лодки после прыжка.

Изобразим на рисунке, что происходило до и после прыжка.

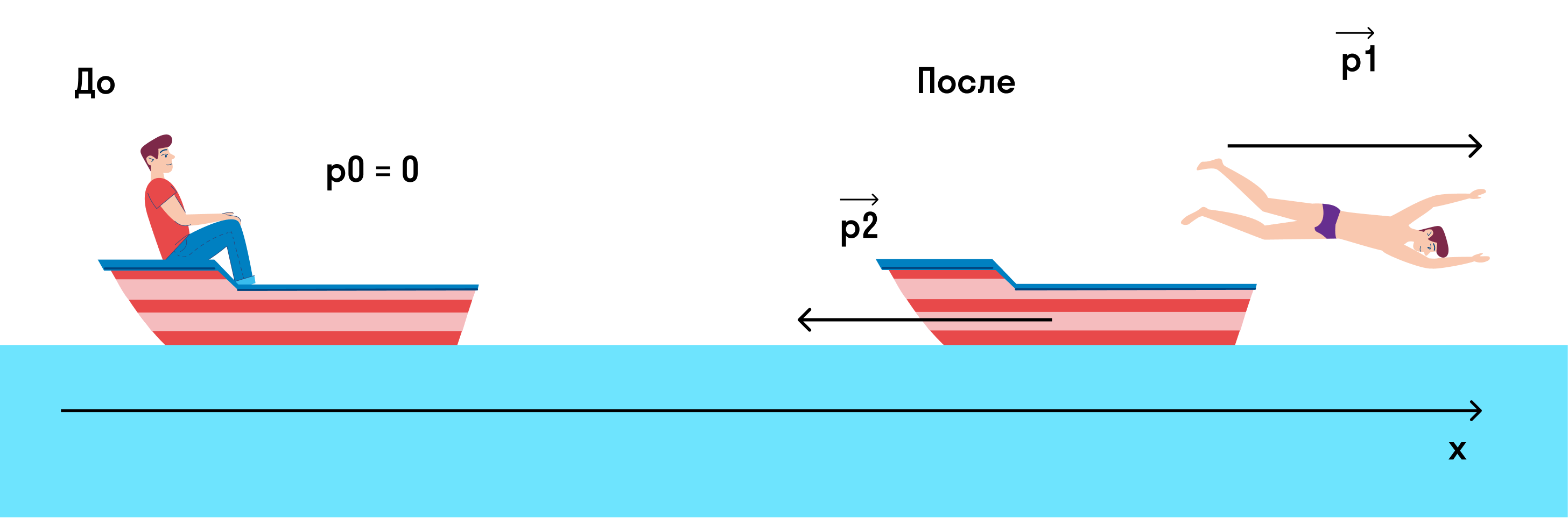
Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид
0 = p1 — p2
p1 = p2

Подставим формулу импульса.
mV1 = MV2

Выразим скорость лодки V2:
V2 = mV1/M

Подставим значения:
V2 = 45*3/270 = 3/6 = ½ = 0,5 м/с

Ответ: скорость лодки после прыжка равна 0,5 м/с

Задачка посложнее

Тело массы m1 = 800 г движется со скоростью v1 = 3 м/с по гладкой горизонталь- ной поверхности. Навстречу ему движется тело массы m2 = 200 г со скоростью v2 = 13 м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.

Решение: Для данной системы выполняется закон сохранения импульса:

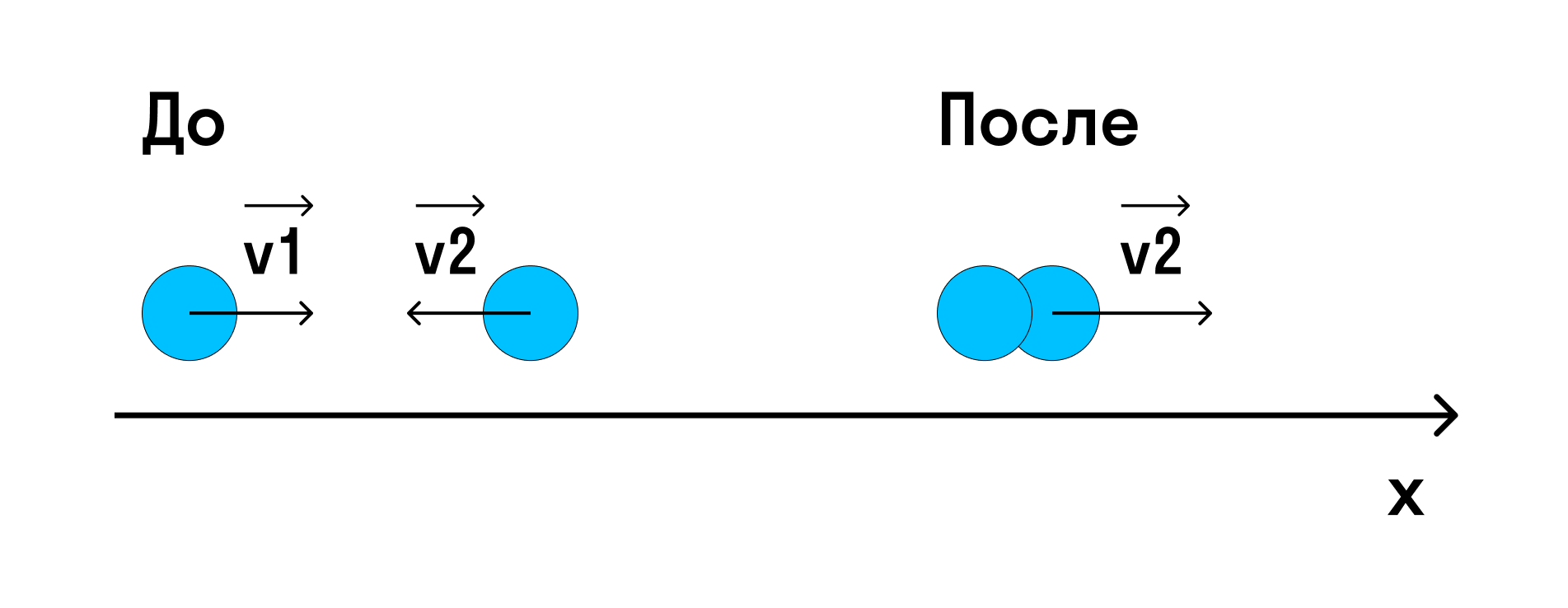
Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.

Спроецируем импульсы на ось х:

После неупругого удара получилось одно тело массы m1 + m2, которое движется с искомой скоростью:

m1v1 — mv2 = (m1 + m2) v

Отсюда находим скорость тела, образовавшегося после удара:

v = (m1v1 — mv2)/(m1 + m2)

Переводим массу в килограммы и подставляем значения:

v = (0,8·3−0,2·13)/(0,8 + 0,2) = 2,4 — 2,6 = -2,6 м/с

В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.

Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на значение получившееся значение.

Ответ: скорость системы тел после соударения равна v = 0,2 м/с.

Второй закон Ньютона в импульсной форме

Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.

Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:

Применим выражение для ускорения

В этих уравнениях слева находится величина a . Так как левые части уравнений равны, можно приравнять правые их части

Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:

В правой части находится Δv =v —v0 — это разница между конечной и начальной скоростью.

Преобразуем правую часть

Раскрыв скобки, получим

Заменим произведение массы и скорости на импульс:

То есть, вектор Δv⋅m – это вектор Δp.

Тогда второй закон Ньютона в импульсной форме запишем так

Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.

Решение:

Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).

Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.

Реактивное движение

В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.

Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.

Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:

Сила F2 называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.

Закон сохранения импульса позволяет оценить скорость ракеты.

mг vг = mр vр,
где mг — это масса горючего,

vг — скорость горючего,

mр — масса ракеты,

vр — скорость ракеты.

Отсюда можно выразить скорость ракеты:

Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.

Источник: exam-ans.ru

Закон сохранения импульса системы тел и положения ее центра масс

Импульс системы тел сохраняется или в двух случаях: если система тел замкнутая 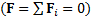и в быстрых процессах (взрыв, распад системы, столкновения тел), для которых интервал времени протекания процесса . Это следует из второго закона Ньютона в дифференциальной и интегральной форме

,

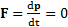Если выполняется условие 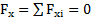, то говорят о замкнутости системы в направлении оси X и сохранении импульса системы в направлении этой оси:

Если начальный импульс системы тел равен нулю и он сохраняется, то есть

(в любой момент t),

то положение ЦМ системы сохраняется: .

Если система замкнута в направлении оси X и ее начальный импульс равен нулю, то в этом случае сохраняется положение ЦМ системы в направлении этой оси: .

Пример 1. Человек массой m переходит с одного конца лодки массой M и длиной l на другой ее конец со скоростью относительно лодки. Найти скорость лодкии ее перемещение x относительно земли, когда человек перейдет на другой конец лодки.

Дано: m, M, l, . Найти:

Решение: Система (лодка и человек +вода) является замкнутой и, в частности, замкнутой в направлении оси X, параллельной поверхности воды (рис.36). Поэтому в системе лодка-человек имеет место закон сохранения импульса, который в начальный момент времени был равен нулю. Наличие сил трения между лодкой и водой не нарушает замкнутость системы в направлении оси X и не влияет на величину перемещения лодки относительно воды.

Во избежание ошибок в знаках проекций векторов задачу будем решать в векторной форме. При движении человека по лодке со скоростью лодка придет в движение со скоростью относительно берега реки и станет движущейся системой отсчета, и скорость человека относительно земли будет равна

. Закон сохранения импульса в системе лодка-человек в системе отсчета, связанной с землей, имеет вид

.

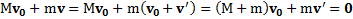
Откуда скорость лодки относительно берега равна . Знак (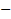) означает анти параллельность векторов и . В скалярной форме .

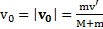Умножая обе части этого равенства на время t движения человека по лодке и обозначая и , получим для смещения лодки относительно берега .

Второй способ решения задачи основывается на сохранении положения ЦМ системы лодка-человек, если ее начальный импульс был равен нулю и сохраняется.

Выберем начало О оси X на противоположном начальному положению человека конце лодки, а ось X направим вдоль лодки в направлении человека. Положение ЦМ системы человек-лодка при t=0 в выбранной СО 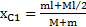, а после его перехода на другой конец лодки 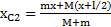. Из условия опять получим . Разделив обе части этого равенства на время t движения человека по лодке и обозначая и 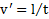придем к прежнему выражению для скорости лодки относительно берега.

Ответ: , .

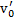
Пример 2. На параллелепипед с массой M, находящимся на горизонтальной гладкой поверхности, лежит тело массой m. Телу сообщают горизонтальную начальную скорость . Найти ускорение, с которым будет двигаться параллелепипед после толчка, и ускорение движения тела относительно параллелепипеда.

Какой путь и за какое время пройдет тело при его движении по поверхности параллелепипеда до остановки? На какое расстояние сместится параллелепипед за это время? Какова начальная скорость параллелепипеда после толчка? Коэффициент трения между телом и параллелепипедом равен μ. Трение между параллелепипедом и горизонтальной поверхностью отсутствует.

Дано: . Найти:

Решение: Для решения задачи выберем две СО: неподвижную XOY, связанную с горизонтальной плоскостью, и движущуюся – , связанную с параллелепипедом. Оси X и направим параллельно горизонтальной плоскости (рис.37) в направлении ускорений параллелепипеда и тела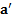

После толчка тела между телом и параллелепипедом возникнут силы трения 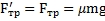и параллелепипед начнет двигаться с ускорением , а на тело подействует сила инерции .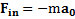

Из второго закона Ньютона для параллелепипеда (рис.37) найдем его ускорениев неподвижной СО , а из второго закона Ньютона для тела его ускорение в движущейся СО . Ускорения тел связаны соотношением .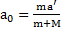

Путь, пройденный телом и время его движения по поверхности параллелепипеда до остановки равны

, .

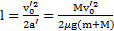Система двух тел является замкнутой и, в частности, замкнутой в направлении осиX. Поэтому в системе имеет место закон сохранения импульса, который в начальный момент времени был равен нулю. С учетом, что в неподвижной СО скорость тела равна закон сохранения импульса в рассматриваемой системе двух тел будет в момент времени t=0 в неподвижной СО иметь вид

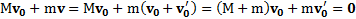
Откуда скорость параллелепипеда после толчка тела равна . В скалярной форме . В произвольный момент времени связь между скоростями тел будет такой же .

Смещение параллелепипеда за время движения тела по его поверхности найдем из закона сохранения положения ЦМ системы. Для этого выберем начало О СО XOY в точке конечного положения тела, а ось X направим в сторону его начального положения (рис.36). Обозначая 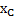положение ЦМ параллелепипеда, получим для начального и конечного положений ЦМ системы: 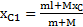, . Из условия приходим к уравнению , из которого находим смещение параллелепипеда .

Уравнения движения тел в неподвижной и движущейся СО в проекциях на направления скоростей их движения и предположения имеют вид

; .

Ответ: , , , , , .

Пример 3. Решить предыдущую задачу в предположении, что начальная скорость была сообщена параллелепипеду (рис.37).

Дано: . Найти:

Решение: Ускорения тел, входящие во второй закон Ньютона, не зависят от их начальной скорости, и они после толчка будут двигаться с теми же ускорениями , .

Закон сохранения импульса в системе будет иметь такой же вид, как и в предыдущем примере. Решая полученное уравнение относительно параметра 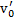, получим для начальной скорости тела . Тогда путь и время движения тела по поверхности параллелепипеда будут равны (конечные выражения отличаются для полученных в предыдущем примере)

, .

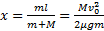
Закон сохранения положения ЦМ системы не изменится и из него получим для смещения параллелепипеда за время движения тела по нему .

Ответ: , , , , , .

Столкновения тел

Различают следующие виды соударений тел: абсолютно неупругое, частично-упругое и абсолютно упругое. Если процесс столкновения быстрый , то имеет место закон сохранения импульса в системе сталкивающихся тел.

Абсолютно неупругое столкновение тел. При этом виде столкновения тела слипаются и после столкновения движутся вместе(рис.38).

Любое столкновение тел описывается законом сохранения импульса и энергии. В данном случае, обозначив импульсы тел до и после столкновения , , 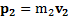и Q – выделившееся при ударе тепло, получим

.

Возведя первое равенство в квадрат, найдем квадрат импульса тел после столкновения, а из второго – выделившееся при ударе тепло

, ,

где – угол между векторами импульсов тел до их столкновения.

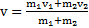
При прямом центральном ударе скорость тел после столкновения , а выделившееся при ударе тепло

,

где 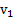и 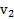– проекции скоростей тел и на направление их движения и имеют знак .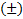

Частично упругое столкновение тел. Ограничимся случаем лобового столкновения тел. При этом виде удара тела не слипаются, но после столкновения у них имеется остаточная деформация (вмятины) и выделяется при ударе тепло . Законы сохранения импульса в проекциях на направление движения тел и энергии в этом случае будут иметь вид

,

где и – скорости тел до и после их столкновения.

Абсолютно упругое столкновение тел. При этом виде столкновения тела после столкновения восстанавливают свою форму и остаточная деформация у них отсутствует, поэтому выделившееся при ударе тепло

Система уравнений, описывающая удар (рис.39), будет иметь вид

, .

Эту систему уравнений можно свести к линейной. Для этого перенесем члены с одинаковыми индексами в одну часть равенства. Получим

, .

Разделив второе уравнение на первое и добавив к полученному уравнению закон сохранения импульса, придем к линейной системе уравнений

, ,

решая которую, получим

, .

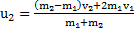В этих уравнениях и – это проекции скоростей тел на выбранное направление оси проецирования X и имеют знак 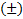. Если при расчетах будет получено 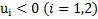, это означает, что скорость тела после столкновения тел направлена противоположно выбранному направлению оси X.

Источник: cyberpedia.su