Теплоход плывет по реке из точки А в точку Б в течение 3 часов, а обратно — в течение 5 часов. Собственная скорость теплохода одинакова в обоих случаях. За какое время из точки А в точку Б доплывет плот?
Эта задача была размещена посетителями в разделе Решаем вместе 15 октября 2007 года.
Обозначим скорость теплохода как vт, а скорость реки как vр.
По сути получается, что теплоход без течения преодолеет это расстояние за 4 часа, по течению — за 3 часа и против — за 5 часов.
Скорость теплохода, плывущего против течения относительно берега равна 3-м скоростям течения.
Ответ: плот проплывет данное растояние за 15 часов.
- задачи с решениями
- кинематика
- механика
- прямолинейное движение
- равномерное движение
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Комментарии
Опубликовано 10 июня, 2009 — 12:39 пользователем Menora
Когда я решала эту задачу сама, я смогла дойти только до того момента, где выясняется, что скорость теплохода в 4 раза больше скорости реки. Но как получить дальнейшие выводы? Помогите, пожалуйста.
Решение задачи про лодку, плывущую через реку
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 13 июня, 2009 — 10:44 пользователем MAX371
Не пойму, как определили, что скорость катера равна 3-м скоростям течения реки.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 13 июня, 2009 — 19:32 пользователем В. Грабцевич
Катер плывет по течению реки:
Плот плывет по течению реки:
Приравняем пройденные расстояния (1) и (2):
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 28 ноября, 2009 — 13:17 пользователем Brain01
Нельзя было по-человечески объяснить? Профессора физических наук, которые никогда не зайдут сюда, и то не сообразят ничего в этих вычислениях.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 28 ноября, 2009 — 16:39 пользователем afportal
Здесь готовят будущих лауреатов Нобелевской премии. Профессор физики — слишком мелкая цель 😉
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 26 февраля, 2021 — 16:29 пользователем СmacXapgukoB
Собственная скорость теплохода одинакова.
Следовательно, разница между 3 и 5 = 2 и есть скорость течения, ну и ответ.
Задача для устного счета 2 класса. Не старше. Из реального учебника. Знаменита она тем, что решение, точнее, ответ порождает юмористические посылы в адрес составителей, ибо:
1) если скорость течения 2, то где теплоход мог плавать 3? Получается, его скорость была отрицательна. ну и:
2) как тогда он плыл против течения?
Немного инфы в тему:
1. Плот имеет массу и потому при сплавке будет плыть с ускорением.
2. Если решается задача по математике и это сопровождается текстами типа «По сути получается, то с решением явная нескладуха».. 😉
Задача на течение реки. Про лодку и плот.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Источник: www.afportal.ru
ОГЭ, Математика.
Геометрия: Задача №471975

Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=8. Найдите площадь ромба.
Решение задачи:
Площадь ромба равна S=ah, где a — сторона ромба, h — высота ромба.
AD=AH+HD=21+8=29.
AD=AB=BC=CD (по определению ромба).
Рассмотрим треугольник ABH.
ABH — прямоугольный (т.к. BH — высота), тогда по теореме Пифагора: AB 2 =BH 2 +AH 2
29 2 =BH 2 +21 2
841=BH 2 +441
BH 2 =400
BH=20
S ромба =AD*BH=29*20=580
Ответ: S ромба =580
Присоединяйтесь к нам.
Вы можете поблагодарить автора, написать свои претензии или предложения на странице ‘Про нас’
Другие задачи из этого раздела
Задача №F63DA7

На стороне AC треугольника ABC отмечена точка D так, что AD=5, DC=7. Площадь треугольника ABC равна 60. Найдите площадь треугольника ABD.
Задача №0DBE64

Радиус окружности с центром в точке O равен 50, длина хорды AB равна 96 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Задача №1A5A9C
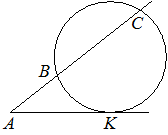
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=4, BC=32. Найдите AK.
Задача №112015
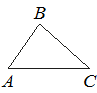
В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.
Задача №705153

Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
Источник: otvet-gotov.ru
Задачи про лодку и течение реки формулы

Задача по физике — 735
2014-06-15 
Лодка переправляется из пункта В, расположенного на одном берегу шириной $l$, в пункт А, расположенный на другом берегу выше по течению на расстоянии $3l/4$ от пункта В (см. рисунок). В процессе переправы лодочник в каждый момент времени направляет нос лодки в направлении пункта А, мотор развивает постоянное усилие. Известно, что скорость, которую имела бы лодка в стоячей воде, равна скорости течения реки. На каком расстоянии от пункта А будет находиться лодка, когда дойдет до середины реки?


То. что лодочник в каждый момент времени ставит нос лодки в направлении города А, означает: вектор скорости лодки относительно воды $overrightarrow$ в каждый момент времени направлен в город А. А вот двигаться в каждый момент времени лодка будет в другом направлении из-за сноса течением. Действительно, поскольку скорость лодки относительно земли $overrightarrow_$ (а именно, она определяет траекторию) определяется законом сложения скоростей
$overrightarrow_ = overrightarrow + overrightarrow$, (1)
где $overrightarrow$ — скорость течения, то из-за разных направлений вектора $overrightarrow$ и величина, и направление вектора $overrightarrow_$ будут различными. На рисунке показана траектория лодки и параллелограммы сложения скоростей, отвечающие закону (1) в ратных точках траектории. Из-за изменения направления скорости $overrightarrow_$ лодка движется по кривой траектории.
По условию величина скорости лодки в стоячей воде и скорости течения одинаковы в каждый момент времени. Поэтому параллелограмм сложения скоростей является ромбом, и, следовательно, в каждый момент времени проекция вектора скорости лодки относительно земли на направление ЛА и на направление течения одинаковы. Поэтому за каждый малый интервал времени лодка приближается к точке А и спускается вниз по течению на одинаковое расстояние. А это значит, что если ввести вспомогательную прямую, расположенную от начального положения лодки ниже по течению на таком же расстоянии, как и точка А (прямая PQ на рисунке), то в каждый момент времени расстояния от лодки до точки А и до прямой PQ будут одинаковы. Поскольку в начальный момент времени лодка расположена на расстоянии $sqrt + (3l/4)^> = 5l/4$ от точки А, то и расстояние от начального положения лодки до прямой PQ равно $5l/4$.
Получим теперь уравнение траектории. Введем систему координат так, как это показано на рисунке, рассмотрим некоторое промежуточное положение лодки $Л_$ и найдем связь ее координат $x$ и $y$. С одной стороны, из приведенных рассуждений следует, что $Л_A = Л_М$. С другой — $ Л_A = sqrt , Л_М = 2l-y $. Поэтому
$sqrt = 2l-y$. (2)
Возводя формулу (2) в квадрат, получаем у равнение траектории
$y = — frac + l$.
Эта траектория — парабола, сдвинутая вдоль оси у на расстояние $l$ (пунктирная кривая на рисунке), с ветвями, направленными против оси у. Отсюда находятся все характерные точки згой траектории. В частности, когда лодка находится на середине реки, ее координата $x$ равна $l/2$. Координату $y$ лодки в этот момент находим из формулы (3)
$y = frac$, (4)
а затем и расстояние от лодки до точки А
$Л_А = sqrt <(l/2)^+ (15l/16)^> = frac l$.
Источник: earthz.ru