Цель: Создание условий для передачи опыта по формированию умения у учащихся по решению задач на движение с помощью уравнения.
Задачи: 1. показать способ решения задач на движение с помощью уравнения;
2. оценить эффективность мастер – класса через рефлексию участников.
Форма проведения: урок — импровизация.
Оборудование: рабочие листы с заданиями, «Билет на выход» для проведения рефлексии.
Ход мастера -класса:
Если человека постоянно приучать усваивать знания и умения в готовом виде, можно и притупить его природные творческие способности — «разучить» думать самостоятельно. В максимальной степени процесс мышления проявляется и развивается при решении проблемных задач.
К сожалению, очень часто мы с вами не предоставляет свободы ученику, когда он пытается ответить на вопрос. Не ждём, а сразу же задаём наводящий вопрос. Можно ли учить так, чтобы каждый ребёнок рассуждал над проблемой своим путём, своим темпом, но при необходимости мог сопоставить свою точку зрения с одноклассниками, может даже изменить её? Конечно же, можно.
Математика | ЗАДАЧА 22 из ОГЭ. Задачи на работу
Помочь ученику раскрыться, лучше использовать свой творческий потенциал помогает создание проблемных ситуаций на уроке.
Проблемное обучение основывается на теоретических положениях американского философа, психолога, педагога Дж. Дьюи (1859-1952). В России дидактику проблемного обучения разработал И.Я. Лернер.
Сегодня под проблемным обучением понимается такая организация учебных занятий, которая предполагает создание под руководством учителя проблемных ситуаций и активную самостоятельную деятельность учащихся по их разрешению, в результате чего происходит творческое овладение профессиональными знаниями, навыками, умениями и развитие мыслительных способностей.
Как же создавать проблемные ситуации?
Вот проблемная ситуация на сегодня.
Эмблема урока: 28k + 30n + 31m = 365
Комментарий учителя к уравнению: Говорят, уравнение вызывает сомнение, но итогом сомнения может быть озарение!
Задание: Найти хотя бы одно решение уравнения.
(Уравнение, красочно оформленное, вывешивается сверху, в центре доски, к концу занятия будет найдено его решение)
Существует множество приёмов создания проблемных ситуаций. Вот некоторые из них:
Создание проблемных ситуаций через
умышленно допущенные учителем ошибки;
формулирование задания в занимательной форме;
выполнение практических заданий;
решение задач на внимание и сравнение;
противоречие нового материала старому, уже известному;
различные способы решения одной задачи;
выполнение небольших исследовательских заданий;
решение задач, связанных с жизнью.
Участникам мастер класса предлагается выбрать задачи на движение из предложенного списка задач.
Задание 1. Выберите задачу на движение и обоснуйте свой ответ.
Лыжник прошел 900 м за 3 минуты, двигаясь с одинаковой скоростью. С какой скоростью двигался лыжник?
Рабочий за 10 часов изготовил 300 деталей. Сколько деталей изготовит рабочий за 40 часов?
Длина прямоугольника 6 м, а ширина в 3 раза меньше. Чему равен периметр и площадь прямоугольника?
Биатлонист пробежал последний круг дистанции за 3 минуты со скоростью, равной 220 м/м. Чему равно данное расстояние?
После выполнения задания предлагается вопрос:
По каким признакам вы определили, что это задачи на движение?
(Ответ: время, скорость, расстояние).
Двое детей одновременно начали есть кашу. Через некоторое время первый ребенок кашу съел, а второй нет, хотя порции были одинаковые. Почему это произошло?
(Ответ: Скорость первого ребенка больше, чем скорость второго).
А эта задача на движение?
Почему нет, ведь в ней присутствуют время и скорость?
(Ответ: Нет такой величины как расстояние).
Задачи на движение 5 класс с решениями и пояснениями
Математические задачи для школьников 5-7 класса. Тема: Отрезок, прямая. Задачи на движение
Задача 1.
На прямой через равные промежутки поставили 10 точек, они заняли отрезок длиной a. На другой прямой через такие же промежутки поставили 100 точек, они заняли отрезок длиной b. Во сколько раз а меньше b?
Расстояние между соседними точками равно a/9 тогда b = (a/9) · 99, то есть b = 11а.
Ответ: a в 11 раз меньше b.
Задача 2.
Длина гардины 1 м 20 см. На каком расстоянии развешаны на этой гардине 6 колец, если расстояние между ними одинаковое?
Шесть колец «разбивают» гардину на 5 промежутков: 120 : 5 = 24 (см)
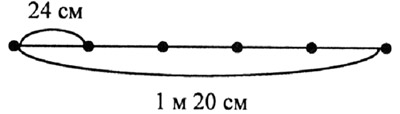
Ответ: на расстоянии 24 см.
Задача 3.
Кузнечик прыгает по прямой большими и малыми прыжками. Большой прыжок составляет 12 см, малый — 7 см. Как ему попасть из точки О в точку А, находящуюся от неё на расстоянии 3 см?
12 · 2 – 7 · 3 = 3 (см).
Ответ: кузнечик должен сделать 2 больших прыжка, а потом обратно 3 маленьких.
Задача 4.
Прямоугольник состоит из двух квадратов, имеющих общую сторону. Его периметр равен 12 см. Найти площадь прямоугольника.
S квадрата = 2 · 2 = 4 см 2 ;
S прямоугольника = 2 · 4 = 8 см 2
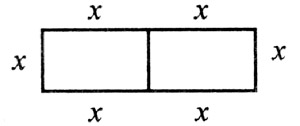
Ответ: площадь прямоугольника 8 см2.
Задача 5.
Проехав треть пути, пассажир лёг спать и спал до тех пор, пока ему не осталось проехать треть того пути, который он проехал спящим. Какую часть всего пути пассажир проехал спящим?
Обозначим через х длину отрезка пути, который пассажир проехал после того, как проснулся. Тогда длина отрезка, который он проехал спящим, равна Зх. Так как 4х составляет 2/3 пути, то весь путь равен 6х.
Следовательно, пассажир спал половину пути.
Ответ: пассажир спал половину пути.
Задача 6.
После того, как пешеход прошёл 1 км и половину оставшегося пути, ему осталось пройти треть всего пути и 1 км. Чему равен весь путь?
Когда пешеход прошёл 1 км и половину оставшегося пути, ему осталось пройти вторую половину оставшегося пути. Но, с другой стороны, по условию задачи ему осталось пройти треть всего пути и 1 км. Значит, после того, как он прошёл 1 км, его путь составил две трети всего пути и ещё 2 км. Но оставшийся путь на 1 км меньше всего пути. Значит, треть всего пути составляет: 1 + 2 = 3 (км).
Весь путь равен 9 км.
Задача 7.
Я еду в трамвае и замечаю, что параллельно трамвайной линии в противоположном направлении проходит мой приятель. Через минуту я вышел из вагона и, чтобы догнать его, пошёл вдвое быстрее его, но в 4 раза медленнее трамвая. Через какое время я догоню приятеля?
Пусть расстояние, которое проходит мой приятель за 1 минуту, есть единица. Тогда расстояние, пройденное мною за 1 минуту, составляет 2 единицы, а расстояние, пройденное трамваем, — 8 единиц. Когда я сошёл с трамвая, расстояние между мною и приятелем составляло: 8 + 1=9 (единиц). Нагоняя приятеля, я каждую минуту сокращал расстояние на 2 — 1 = 1 (единицу). Следовательно, чтобы догнать приятеля, мне потребовалось 9_1=9 (минут).
Задача 8.
Наблюдатель, стоящий на мосту длиной 150 м, заметил, что поезд прошёл мимо него за 10 секунд, а на движение по мосту затратил 25 секунд (считая с момента вступления на мост тепловоза и до момента, когда последний вагон сошёл с моста). Найти длину и скорость поезда.
На прохождение расстояния, равного длине поезда, поезд затратил 10 секунд, а на прохождение такого же расстояния плюс 150 м — 25 секунд. Значит, скорость поезда равна: 150 : (25 — 10) = 10м/с = (10·60·60)/1000 = 36км/ч. Длина поезда: 10 • 10= 100 (м).
Ответ: Длина поезда — 100 м, скорость — 36 км/ч.
Задача 9.
Инженер ежедневно приезжает поездом на вокзал в 8 часов утра. Точно в 8 часов к вокзалу подъезжает автомобиль и отвозит инженера на завод. Однажды инженер приехал на вокзал в 7 часов утра и пошёл навстречу машине. Встретив машину, он сел в неё и приехал на завод на 20 минут раньше, чем обычно. Определите показания часов в момент встречи инженера с машиной.
По сравнению с обычным своим рейсом машина не проехала на этот раз расстояние от места встречи с инженером до вокзала и обратно — от вокзала до места встречи. Экономия составила 20 минут. Значит, место встречи находилось в 10 минутах езды до вокзала, куда машина должна была прибыть в 8 часов. Следовательно, в момент встречи часы показывали 7 часов 50 минут.
Ответ: показания часов — 7 часов 50 минут.
Задача 10.
Кузнец бьёт молотом по наковальне 4 раза в течение 12 секунд. Сколько ему потребуется времени, чтобы нанести по наковальне 8 ударов?
Удар кузнеца молотом можно считать мгновенным. Первый удар он производит в первое мгновение — в первую секунду, а последний — четвёртый — в последнюю, двенадцатую секунду. Значит, за 12 : 3 = 4 (секунды) он делает один удар (промежуток между двумя ударами). За 24 секунды он успевает выполнить только 7 ударов. Значит, на нанесение восьми ударов ему потребуется 28 секунд.
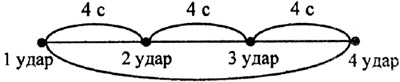
Ответ: 28 секунд.
Задача 11.
Кузнечик прыгает по прямой: первый прыжок на 1 см, второй — на 2 см и т. д. Может ли он после 25-го прыжка вернуться в точку, с которой начал?
Чтобы кузнечику после 25-го прыжка оказаться в начальной точке, необходимо преодолеть длину, равную чётному числу. Но это невозможно, так как 1 + 2 + 3 + . + 13 + . + 25 = (1 + 25) • 12 + 13 — нечётное число.
Задача 12.
Сколько мостов соединяют 40 островов, если известно, что каждый остров соединяется с остальными островами ровно тремя мостами?
На каждом острове имеется 3 конца мостов, следовательно, на всех островах всего 120 концов мостов, самих же мостов будет ровно в 2 раза меньше, то есть 60 мостов.
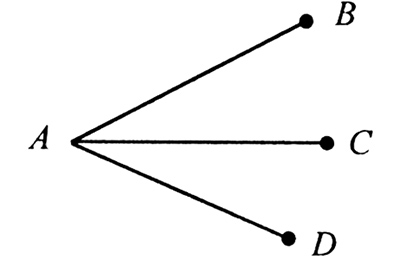
Ответ: 60 мостов.
Задача 13.
Нарисуйте 8 точек и соедините их отрезками так, чтобы отрезки не пересекались и через каждую точку проходило ровно 4 отрезка.
Источник: ped-kopilka.ru
Задачи по математике про лодки

Цели и задачи урока: ознакомить учащихся со спецификой решения задач на движение при необходимости учета течения реки, и выработать устойчивый навык противостояния подобным задачам.
Предметные результаты: знать понятия: собственная скорость катера, скорость течения реки, уметь находить скорость катера по течению и против течения, перевод единиц времени и скорости.
Метапредметные и личностные результаты: воспитывать познавательный интерес к предмету, уметь выбирать наиболее эффективные способы решения поставленных задач.
Здравствуйте. Очень часто человеку приходится совершать движения по воде: реке, озеру, морю. И всегда его интересовали длина пути и время, затраченное на его преодоление.
Представим себе, что на улице весна. Солнце растопило снег. Появились лужицы и побежали ручьи. Сделаем два бумажных кораблика и пустим один из них в лужу, а второй — в ручей. Что же произойдет с каждым из корабликов?
В луже кораблик будет стоять на месте, а в ручейке — поплывет, так как вода в нем «бежит» к более низкому месту и несет его с собой. То же самое будет происходить с плотом или лодкой.
В озере они будут стоять на месте, а в реке – плыть.
Рассмотрим первый вариант: лужа и озеро. Вода в них не движется и называется стоячей.
Кораблик поплывет по луже только в том случае, если мы его подтолкнем или если подует ветер. А лодка начнет двигаться в озере при помощи весел или если она оснащена мотором, то есть за счет своей скорости. Такое движение называют движением в стоячей воде.
Отличается ли оно от движения по дороге? Ответ: нет. А это значит, что мы с вами знаем как действовать в этом случае.
Чем же отличается движение по озеру от движения по реке?
Вспомним бумажный кораблик в ручье. Он плыл, потому что вода в нем движется.
Такое движение называют движением по течению. А в обратную сторону – движением против течения.
Итак, вода в реке движется, а значит имеет свою скорость. И называют ее скоростью течения реки. (Как ее измерить?)
Задача 1. Скорость течения реки равна 2 км/ч. На сколько километров река относит любой предмет (щепку, плот, лодку) за 1час, за 4 часа?
Ответ: 2 км/ч, 8 км/ч.
Каждый из вас плавал в реке и помнит, что по течению плыть гораздо легче, чем против течения. Почему? Потому, что в одну сторону река «помогает» плыть, а в другую — «мешает».
Те же, кто не умеет плавать, могут представить себе ситуацию, когда дует сильный ветер. Рассмотрим два случая:
1) ветер дует в спину,
2) ветер дует в лицо.
И в том и в другом случае идти сложно. Ветер в спину заставляет бежать, а значит, скорость нашего движения увеличивается. Ветер в лицо сбивает нас, притормаживает. Скорость при этом уменьшается.
Остановимся на движении по течению реки. Мы уже говорили о бумажном кораблике в весеннем ручье. Вода понесет его вместе с собой. И лодка, спущенная на воду, поплывет со скоростью течения. Но если у нее есть собственная скорость, то она поплывет еще быстрее.
Следовательно, чтобы найти скорость движения по течению реки, необходимо сложить собственную скорость лодки и скорость течения.
Задача 2. Собственная скорость катера равна 21 км/ч, а скорость течения реки 4 км/ч. Найдите скорость катера по течению реки.
Теперь представим себе, что лодка должна плыть против течения реки. Без мотора или хотя бы весел, течение отнесет ее в обратную сторону. Но, если придать лодке собственную скорость ( завести мотор или посадить гребца), течение будет продолжать отталкивать ее назад и мешать двигаться вперед со своей скоростью.
Поэтому, чтобы найти скорость лодки против течения, необходимо из собственной скорости вычесть скорость течения.
Задача 3. Скорость течения реки равна 3 км/ч, а собственная скорость катера 17 км/ч. Найдите скорость катера против течения.
Рассмотрим, как можно использовать эти приобретенные нами знания.
Задача 4. Теплоход, двигаясь против течения реки, за 4 ч прошёл 104 км. Скорость течения реки 2 км/ч. Вычислите собственную скорость теплохода.
Ну что же, двигаясь против течения реки, теплоход развил скорость 104_4=26 км/ч. При этом мы уже обсуждали что эта скорость – разность собственной скорости теплохода и скорости течения. Значит собственная скорость теплохода равна 26+2=28 км/ч.
Задача 5. Расстояние между двумя причалами 24 км. Сколько времени потратит моторная лодка
на путь от одного причала до другого и обратно, если её собственная скорость 10 км/ч, а скорость течения 2 км/ч?
Итак, путь по течению лодка проделает со скоростью 12 км/ч, обратно – 8 км/ч, значит общее время будет равняться сумме соответствующих отношений: 24:12+24:8=2+3=5 ч.
Задача 6. Моторная лодка проплыла 48 км по течению за 3 ч, а против течения — за 4 ч. Найдите скорость течения.
Давайте посмотрим: скорость по течению по условию задачи составляет 48_3=16 км/ч, а против течения 48_4=12 км/ч. Разница между ними составляет 4 км/ч и является удвоенной скоростью течения. Таким образом скорость течения 2 км/ч.
Задача 7. Из двух пунктов реки, расстояние между которыми равно 42 км, навстречу друг другу
движутся две моторные лодки. Лодка, идущая по течению, собственная скорость которой равна 18 км/ч,
до встречи шла 1 ч, другая лодка, собственная скорость которой равна 17 км/ч, до встречи шла 2 ч.
Найдите скорость течения реки.
Давайте посмотрим. Первая лодка за час успела пройти 18 км и ещё то расстояние на которое её отнесла река своим течением. Вторая лодка прошла бы 34 км, если бы её не отнесло назад на удвоенное расстояние, на которое её за час отнесла та же река. Значит вместе они прошли 52 км, за вычетом одного уже обсужденного нами расстояния. Так как они всё-таки встретились, означает что разница между 52 и 42 километрами, это и есть наше расстояние сноса течением реки за час.
Ну значит скорость течения реки – 10 км/ч
Задача 1. Расстояние между пристанями — 336 км. Сколько времени потребуется теплоходу,
чтобы проплыть туда и обратно, если его скорость по течению 28 км/ч, а скорость течения 4 км/ч?
Задача 2. Расстояние между двумя причалами 36 км. Сколько времени потратит моторная лодка
на путь от одного причала до другого и обратно, если её собственная скорость 15 км/ч, а скорость течения 3 км/ч?
Задача 3. Катер проплыл 72 км между пристанями по течению за 2 ч, а против течения за
3 ч. За сколько часов это расстояние проплывут плоты?
Источник: xn—-7sbbzn3afjs.xn--p1ai