Найди верный ответ на вопрос ✅ «лодка плывет по реке со скоростью 8.4 км ч. впереди нее на расстоянии 2 км плывет плот. найди скорость плота если известно что лодка . » по предмету Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Новые вопросы по математике
2 тыс=. Дес 2 дес. тыс.=тысяч. 5 сот тысяч=дес. тыс 3 дес. тыс=сот тысяч 10 дес=ед 20 дес. тыс=сот тысяч
В треугольнике авс сторона ав=корень из 43, вс=корень из 59, ас=4. Найдите величину наибольшего угла
Сколько существует различных расположений 15 монеток, в которых нет 2 подряд идущих орлов?
Стороны треугольника равны 3/8 м, 1/2 м, 5/6 м. Найти периметр.
Всем привет. В магазине в 1 день продали 35%, во 2 — 28%всеховощей, А в 3 — оставшиеся 333 кг. Сколько кг овощейбыло в магазине первоначально?
Главная » Математика » лодка плывет по реке со скоростью 8.4 км ч. впереди нее на расстоянии 2 км плывет плот. найди скорость плота если известно что лодка догнола его через 24 минуты ответ 3.4 км ч
98% не решат эту задачу в уме Задача на движение по реке Математическая медитация
Источник: urokam.net
Задачи на скорость реки плота и лодки

Нужно ли для ответа на требование задачи знать скорость движения плота, каторая совпадает со скоростью течения реки?
Можно ли найти расстояние, которое преодолел катер за 2 часа движения вверх по течению реки, если мы знаем только скорость катера в стоячей воде? Почему? Что для этого нужно еще знать?
Вычисли это расстояние, если скорость течения реки 2 км/ч.
Ответ оставил Гость
На каком расстоянии они окажутся друг от друга через 2 ч движения, если скорость катера в стоячей воде 20 км/ч?
20 * 2 = 40 (км) — расстояние между катером и плотом через два часа.
Нужно ли для ответа на требование задачи знать скорость движения плота, которая совпадает со скоростью течения реки?
Как видно из решения, нет. Дело в том, что и катер, и плот сносятся течением одинаково, а, поскольку нас интересует их относительное расстояние, то про скорость течения можно забыть. Физики называют подобные рассуждения принципом относительности Галилея.
Показать, что скорость течения не нужна, можно и при помощи формул.
Пусть x (км/ч) — скорость течения реки.
Тогда скорость плота относительно берега x, скорость катера 20 — x.
За 2 часа плот пройдет 2x (км), катер 2(20 — x) (км)
Расстояние между ними равно 2x + 2(20 — x) = 2x + 2 * 20 — 2x = 40 (км) и не зависит от x.
Можно ли найти расстояние, которое преодолел катер за 2 часа движения вверх по течению реки, если мы знаем только скорость катера в стоячей воде? Почему? Что для этого нужно еще знать?
Нет, нельзя. По сравнению с первой ситуацией, когда мы искали расстояние между сносимым течением плотом и сносимым течением катером, тут нужно искать расстояние между сносимым течением катером и неподвижным берегом. Поэтому тут важно знать скорость течения реки.
Математика По течению реки поплыл плот, а через 5 часов 20 мин после этого – моторная лодка, которая
Это и видно и из полученных формул: расстояние, пройденное катером, равно 2(20 — x) км и, конечно, зависит от x.
Вычисли это расстояние, если скорость течения реки 2 км/ч.
1) 20 — 2 = 18 (км/ч) — скорость катера против течения.
2) 18 * 2 = 36 (км) — прошёл катер.
Можно и по-другому: мы знаем, что расстояние между катером и плотом 40 км, тогда, найдя, сколько прошел плот, найдем, сколько прошел катер.
1) 2 * 2 = 4 (км) — прошёл плот.
2) 40 — 4 = 36 (км) — прошёл катер.
Ответ . Расстояние между катером и плотом 40 км, катер прошёл 36 км.
Оцени ответ

Источник: www.shkolniku.com
Задание 11. ЕГЭ. Расстояние между пристанями А и В равно 135 км. Из А в В по течению реки отправился плот, а через 2 часа вслед за ним отправилась моторная лодка


Задание. Расстояние между пристанями А и В равно 135 км. Из А в В по течению реки отправился плот, а через 2 часа вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 80 км. Найдите скорость моторной лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
Решение:
Пока моторная лодка проделала путь из А в В и обратно, плот проплыл 80 км. Так как скорость течения реки 4 км/ч, то плот затратил на этот путь 80 : 4 = 20 ч.
Учитывая, что моторная лодка отправилась через 2 часа после плота, то время в пути моторной лодки будет равно 20 – 2 = 18 ч.
Пусть x – скорость моторной лодки в неподвижной воде,
тогда скорость лодки по течению реки равна (x + 4) км/ч,
а скорость лодки против течения реки равна (x – 4) км/ч.
На путь из А в В по течению реки моторная лодка затратила 135/(x + 4) ч.,
на обратный путь против течения реки моторная лодка затратила 135/(x – 4) ч.
Время моторной лодки в пути равно 18 ч., получим уравнение:
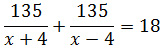
Упростим уравнение, для этого умножим обе части уравнения на (x + 4)·(x – 4), получим
135·(x + 4) + 135·(x – 4) = 18·(x + 4)·(x – 4)
135x + 540 + 135x – 540 – 18x 2 + 288 = 0
18x 2 – 270x – 288 = 0
D = (-270) 2 – 4·18·(-288) = 93636
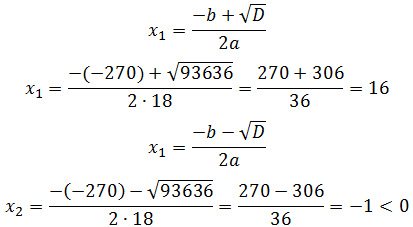
Так как скорость лодки не может быть отрицательной величиной, получим ее скорость в неподвижной воде 16 км/ч.
Ответ: 16
P.S. Для извлечения квадратного корня из числа 93636 можно воспользоваться следующим способом:
Определим, между какими числами лежит результат корня. Для этого разобьем число 93636 на группы по две цифры, начиная справа налево, у нас получилось три группы чисел 9.36.36, т. е. необходимо подбирать числа кратные 100. Результат корня будет лежать между числами 300 и 400, так как
300 2 = 90000 и 400 2 = 160000.
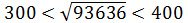
Далее определяем, как число 93636 расположено относительно чисел 90000 или 160000. Получается, что число 93636 расположено ближе к 90000, чем к 160000. Поэтому результат корня будет меньше 350.
Пробуем возводить в квадрат числа 350, 340, … Так как число 93636 находится очень близко к числу 90000, то можно начинать возводить в квадрат с 320 и т. д. Это умножение легко выполнить в столбик.
320 2 = 320·320 = 102400
310 2 = 310·310 = 96100
300 2 = 300·300 = 90000
Можно сделать вывод, что
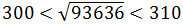
Так как число 93636 оканчивается цифрой 6, то в квадрат необходимо возводить числа, расположенные между 300 и 310 и оканчивающиеся на 4 или 6, таких чисел два:
304 2 = 304·304 = 92416
306 2 = 306·306 = 93636
Источник: bezikev.ru