Пример 8.1. Лодка со стоящим на ней человеком имеет скорость v0. Определить, пренебрегая сопротивлением воды, с какой скоростью v будет двигаться лодка, если человек пойдет по ней вперед со скоростью u относительно лодки. Масса человека равна m, а масса лодки – M. На какую величину L переместится покоившаяся лодка при перемещении по ней человека на l?
Применим закон изменения импульса в интегральной форме:
 2 –
2 –  1 =
1 = 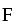 t . (8.1)
t . (8.1)
Рассмотрим систему «человек – лодка». Первое состояние – человек стоит на лодке; второе состояние – человек идет по лодке. Соотношение (8.1) справедливо в инерциальной системе отсчета. Таковой можно считать воду, относительно которой задана скорость v0. Найдем импульсы, входящие в формулу (8.1):
Закон сохранения импульса. Решение задач. 9 класс
 1 = (m + M)
1 = (m + M)  0 ,
0 , 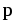 2 = M
2 = M  +m (
+m (  +
+  ) . (8.2)
) . (8.2)
Здесь  +
+  – скорость человека относительно воды, найденная позакону сложения скоростей.
– скорость человека относительно воды, найденная позакону сложения скоростей.

В правой части (8.1) содержатся лишь силы тяжести и архимедова сила. Проекции этих сил на горизонтальное направление равны нулю, поэтому удобно проецировать уравнение (8.1) на ось x, сонаправленную со скоростью 0:
Из (8.3) видно, что при достаточно большой скорости u величина vX окажется отрицательной, то есть лодка станет двигаться в направлении, противоположном первоначальному.
При v0 = 0 формула (8.3) дает скорость движения покоившейся первоначально лодки, по которой пошел человек. Если он идет со скоростью u в течение времени t = l / u , то лодка переместится в обратном направлении на величину L = vX t , следовательно,
L = m l / (M + m) . (8.4)
Получившийся таким образом ответ на второй вопрос задачи основан на предположении о равномерном движении человека. Между тем этот ответ справедлив при произвольном изменении скорости в процессе движения. В этом убеждает решение второй части задачи, основанное на использовании понятия «центра масс».
Центром масс называют такую точку, скорость которой, умноженная на массу всей системы, равна импульсу системы. В рассматриваемой задаче 
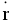 C , где
C , где 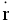 C – радиус-вектор центра масс.
C – радиус-вектор центра масс.
Закон сохранения импульса. Практическая часть — решение задачи. 9 класс.
Закон изменения импульса в дифференциальной форме, d /dt =
/dt = 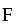 , приводит к заключению, что проекция импульса системы «человек – лодка» остается неизменной. В ситуации, о которой говорится во второй части задачи, эта проекция остается равной нулю:
, приводит к заключению, что проекция импульса системы «человек – лодка» остается неизменной. В ситуации, о которой говорится во второй части задачи, эта проекция остается равной нулю:

(m + M) C = 0 . (8.5)
Отсюда следует, что центр масс системы остается на месте (xC = const) при любых движениях ее частей.
Используя известную формулу, определяющую радиус-вектор центра масс,
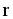 С = ( mi
С = ( mi  i) / ( mi) , (8.6)
i) / ( mi) , (8.6)
получим xC = (m xЧ + M xЛ) (M + m) = const , (8.7)
где xЧ и xЛ – координаты человека и лодки соответственно. Для приращений этих координат соотношение (8.7) дает
Приращения координат в данной задаче имеют следующие значения: xЛ = – L ; xЧ = l – L. Подставляя их в (8.8), приходим к (8.4). Получен прежний ответ, но при этом не накладывалось никаких ограничений на характер движения человека.
Пример 8.2. В сильный снегопад от железнодорожного состава, идущего со скоростью v0, оторвалась платформа. Считая, что количество снега, выпавшего на платформу в единицу времени, равно q, определить, через какое время t платформа остановится, если ее начальная масса равна m0, а коэффициент сопротивления движению в отсутствии снега равна .
Платформу можно считать частицей с переменной массой, и применить к описанию ее движения уравнение Мещерского в проекции на направление начальной скорости:
m dv / dt = FX + u dm / dt . (8.9)
Здесь v – проекция скорости платформы, m – ее масса, u = – v – проекция скорости налипающих частиц снега относительно платформы, dm / dt = q, FX = – m g . Так что (8.9) принимает вид
m dv / dt = – m g – v q . (8.10)
При неизменной интенсивности снегопада (dv / dt = q = const) масса растет со временем по закону
Подставляя (8.11) в (8.10), получим дифференциальное уравнение
(m0 + q t) dv / dt + v q = – g ((m0 + q t) . (8.12)
Решение такого неоднородного уравнения представляет собой, как известно из математики, сумму двух слагаемых: v = v 1+ v2 , где v 1 – общее решение уравнения (8.12) без правой части (однородного), а v2 – одно из частных решений уравнения (8.12) с правой частью.
Переменные v1 и t однородного уравнения легко разделяются, и после интегрирования получается
где v10 – произвольная постоянная.
Поскольку правая часть неоднородного уравнения (8.12) представляет собой линейную относительно t функцию, то частное решение этого уравнения следует искать тоже в виде линейной функции:
Постоянные A и B должны быть подобраны так, чтобы при подстановке v = v2 в (8.12) получилось тождество. Сделав такую подстановку и приравнивая коэффициенты при одинаковых степенях t в обеих частях равенства, получим
A = – g m0 / (2 q) и B = – g / 2 . (8.15)
Подставив (8.13) и (8.14) с постоянными (8.15) в (8.12), найдем общее решение этого уравнения:
v = m0 v10 / ( m0 + q t) – g m0 / (2 q) – g t / 2 . (8.16)
Произвольная постоянная v10 находится из начального условия vt = 0 = v0 :
Осталось лишь подставить в (8.16) выражение (8.17), а также v = 0 и решить получающееся квадратное относительно t уравнение
Это уравнение имеет два корня:

t = .
Лишь верхний знак должен быть оставлен в ответе, так как иной корень дает t < 0, что не имеет физического смысла.
Задачи для самостоятельного решения
Задача 8.1 Ш. Тележка с песком массой M катится горизонтально со скоростью vТ. В нее ударяет и застревает в песке снаряд массой m, который падал со скоростью vС под углом к горизонту навстречу тележке. Как будет двигаться тележка после удара?
Ответ : Проекция скорости тележки на направление первоначального движения vx = (M vТ – m vС cos ) / ( M + m) .

Задача 8.2. Брусок A массой m1 может скользить по гладкой горизонтальной плоскости. К бруску шарнирно присоединен невесомый стержень длины l, на конце которого укреплен груз B массой m2 (рис. 64). Стержень отклонен на угол и отпущен без начальной скорости.
Определить координату xA тела A в зависимости от угла отклонения (рис. 64), полагая, что xA = 0 = 0. Найти также траекторию движения груза B.
Задача 8.3. Самолет с воздушно-реактивным двигателем совершает прямолинейный горизонтальный полет. Двигатель захватывает в единицу времени определенную массу q воздуха и приблизительно столько же отбрасывает назад со скоростью u относительно самолета. Определить скорость самолета как функцию времени, пренебрегая силами сопротивления. Масса самолета – m0.
Скорость самолета в момент включения двигателя пренебрежимо мала.
Ответ : v = u (1 – exp (– q t / m) ) .
Задача 8.4. Космический корабль движется в безвоздушном пространстве вдали от тяготеющих масс со скоростью  0.
0.
В некоторый момент времени включается двигатель корабля, который выбрасывает в единицу времени массу q со скоростью 
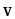 0. Какова будет скорость v корабля спустя время t после включения двигателя? Какой путь s за это время пройдет корабль? Масса корабля до включения двигателя была равна m0.
0. Какова будет скорость v корабля спустя время t после включения двигателя? Какой путь s за это время пройдет корабль? Масса корабля до включения двигателя была равна m0.
Ответы : v = v0 + u ln 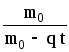 ; s = (v0 + u ) t –
; s = (v0 + u ) t –  ln
ln .
.
Задача 8.5. Как с течением времени должна изменяться масса реактивного автомобиля, чтобы он из состояния покоя двигался горизонтально с постоянным ускорением w? Сила сопротивления пропорциональна скорости (коэффициент пропорциональности – k). Скорость истечения продуктов сгорания топлива равна u. Начальная масса автомобиля равна m0.
Ответ : m = (m0 – k u / w) exp (– w t / u) – k t + k u / w .
Задача 8.6. В задаче 6.6 (рис. 53) найти силу F давления блока на ось при движении грузов.

Ответ : F = g (m1 + m2 + m) – .
Задача 8.7. Змея массой M и длиной L лежит на чашке уравновешенных весов. Определить, какую гирю нужно положить на противоположную чашку весов, чтобы не нарушилось равновесие, когда змея начнет поднимать голову вертикально вверх со скоростью v.
Ответ : m = M v 2 / (g L).
Задача 8.8 *). Свернутую в клубок цепочку положили на край горизонтального гладкого стола так, что маленький кусочек цепочки свесился со стола. Как с течением времени t будет меняться длина x свешивающейся части цепочки?
Ответ : x = g t 2 / 6 .
Задача 8.9. По боковым сторонам прямоугольного клина, опирающегося основанием BC на гладкую горизонтальную плоскость, могут скользить два бруска массами m1 и m2 (рис. 65). Бруски связаны невесомой нерастяжимой нитью переброшенной через блок, укрепленный на ребре A. Масса клина с блоком равна M. Найти перемещение x клина по горизонтальной плоскости при опускании на высоту h бруска, скользящего по грани, наклоненной под углом к горизонту.

Задача 8.10. Ракета движется вверх в однородном поле тяжести с постоянным ускорением w = 3 g. Скорость истечения продуктов сгорания топлива относительно ракеты равна u. Определить, через сколько времени t масса ракеты уменьшится вдвое.
Ответ : t = (u ln 2) / (4 g) .

Задача 8.11. На однородный цилиндр, могущий свободно вращаться вокруг горизонтальной оси, намотан трос, на свободном конце которого подвешен груз массой m. Определить силу давления на ось цилиндра, если груз опускается с ускорением w, а масса цилиндра равна M.
Ответ : F = (M + m) g – m w .
Задача 8.12. Тело переменной массы, имея начальную скорость, равную нулю, движется с постоянным ускорением w по горизонтальным направляющим. Скорость u истечения газов относительно тела постоянна. Определить, пренебрегая сопротивлением, путь s, пройденный телом до того момента, когда его масса уменьшится в k раз.
Ответ : s = (u ln k) 2 / (2 w) .
Задача 8.13. Груз массой m1 поднимается при помощи блочного приспособления, изображенного на рисунке 66. Определить силу F давления на ось неподвижного блока, если груз массой m2 опускается с ускорением w. Трением и массой блоков пренебречь.
Источник: studfile.net
Человек, сидящий в лодке, бросает камень под углом 60 градусов к горизонту. Масса
Человек, сидящий в лодке, бросает камень под углом 60° к горизонту. Масса камня 1 кг, масса человека с лодкой 150 кг, начальная скорость камня 10 м/с. Найти расстояние между точкой падения камня и лодкой в момент, когда камень коснулся воды. Трением лодки о воду пренебречь.
Задача №2.10.37 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(alpha=60^circ), (m=1) кг, (M=150) кг, (upsilon_0=10) м/с, (L-?)
Решение задачи:
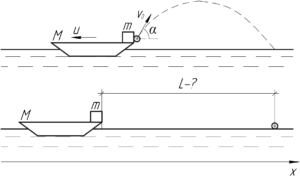
После того, как человек бросит камень, лодка тоже придет в движение. Так как на систему “лодка – человек – камень” не действуют горизонтальные силы, то суммарный импульс в проекции на ось (x) должен сохраняться по закону сохранения импульса:
Отсюда скорость лодки (u) равна:
До падения в воду камень будет двигаться время (2t), где (t) – это время подъема камня до наивысшей точки своей траектории, равное:
За время (2t) лодка и камень удалять друг от друга на расстояние (L), которое можно найти по такой формуле:
[L = left( <<upsilon _0>cos alpha + u> right) cdot 2t]
Подставим (1) и (2) в эту формулу, тогда получим:
Подставим исходные данные в формулу и посчитаем ответ:
[L = frac^2> cdot sin 120^circ >>>left( >> right) = 8,72; м = 872; см]
Ответ: 872 см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник: easyfizika.ru
Задачи на импульс с лодкой
Формулы для решения задач по теме «Закон сохранения импульса. Задачи ЕГЭ».


ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Тело массой 2 кг свободно падает без начальной скорости с высоты 5 м на горизонтальную поверхность и отскакивает от нее со скоростью 5 м/с. Найдите абсолютную величину изменения импульса тела при ударе, g = 10 м/с 2 .

Задача 2. Мячик массой 200 г летел со скоростью 20 м/с. После удара о стенку он отскочил под прямым углом к прежнему направлению со скоростью 15 м/с. Найдите модуль изменения импульса мячика при ударе.
Посмотреть РЕШЕНИЕ и ответ

Задача 3. Стальной шарик массой 0,1 кг падает на горизонтальную плоскость с высоты 0,2 м и отскакивает после удара снова до высоты 0,2 м. Найдите среднюю силу давления шарика на плоскость при ударе, если его длительность 0,04 с. g = 10 м/с 2 .
Посмотреть РЕШЕНИЕ и ответ

Задача 4. Стальной шарик массой 40 г, летящий горизонтально со скоростью 20 м/с, ударяется о наклонную плоскость, составляющую угол 30° с горизонтом. Считая удар абсолютно упругим, найдите среднюю силу взаимодействия шарика с наклонной плоскостью. Продолжительность удара 0,01 с. Действием силы тяжести за время удара пренебречь.
Посмотреть РЕШЕНИЕ и ответ

Задача 5. Какова средняя сила давления на плечо при стрельбе из автомата, если масса пули 10 г, а скорость пули при вылете 300 м/с? Автомат делает 300 выстрелов в минуту.
Посмотреть РЕШЕНИЕ и ответ

Задача 6. Ракета массой 2 т неподвижно висит над землей, выбрасывая вниз реактивную струю со скоростью 1250 м/с. Какая масса газов выбрасывается в струе за 1 с? g = 10 м/с 2 .
Посмотреть РЕШЕНИЕ и ответ

Замечание. Если ракета движется с ускорением, формула для реактивной силы имеет такой же вид. Проще всего убедиться в этом, перейдя в систему отсчета, в которой ракета в данный момент покоится.
Задача 7. Тонкую мягкую цепочку массой 200 г удерживают за один конец так, что другой ее конец касается стола. Цепочку отпускают, и она падает на стол. Считая, что все элементы цепочки, находящиеся в воздухе, падают свободно, найдите силу давления на стол в тот момент, когда в воздухе находится половина цепочки, g = 10 м/с 2 .
Посмотреть РЕШЕНИЕ и ответ

Задача 8. Конькобежец катил груженные сани по льду со скоростью 5 м/с, а затем толкнул их вперед и отпустил. С какой скоростью (в см/с) покатится конькобежец непосредственно после толчка, если скорость саней возросла до 8 м/с? Масса саней 90 кг, масса человека 60 кг. В ответе укажите модуль скорости.
Посмотреть РЕШЕНИЕ и ответ

Задача 9. Три лодки массами 100 кг каждая идут одна за другой с одинаковыми скоростями. Из средней лодки одновременно в переднюю и заднюю бросают горизонтально со скоростью 2,2 м/с относительно лодки грузы массой 10 кг каждый. Найдите величину относительной скорости (в см/с) передней и задней лодок после попадания в них грузов.
Посмотреть РЕШЕНИЕ и ответ

Задача 10. От поезда, идущего с постоянной скоростью 64 км/ч, отделяется пятая часть состава. Через некоторое время скорость отделившихся вагонов уменьшилась в 2 раза. Считая, что сила тяги при разрыве не изменилась, найдите скорость (км/ч) головной части поезда в этот момент. Сила трения пропорциональна весу.
Посмотреть РЕШЕНИЕ и ответ

Задача 11. Снаряд, летящий с некоторой скоростью, распадается на два осколка. Скорость большего осколка по величине равна начальной скорости снаряда и направлена перпендикулярно к ней. Скорость другого осколка по величине в 5 раз больше первоначальной. Найдите отношение масс осколков.
Посмотреть РЕШЕНИЕ и ответ

Задача 12. Снаряд массой 50 кг, летящий под углам 30° к вертикали со скоростью 600 м/с, попадает в платформу с пескам и застревает в ней. Найдите скорость платформы после попадания снаряда. Масса платформы 950 кг. Трением между платформой и рельсами пренебречь.
Посмотреть РЕШЕНИЕ и ответ

Задача 13. В ящик с песком массой 9 кг, соскальзывающий с гладкой наклонной плоскости, попадает горизонтально летящее ядро массой 3 кг и застревает в нем. Найдите скорость ящика сразу же после попадания ядра, если непосредственно перед попаданием скорость ящика равнялась 6 м/с, а скорость ядра 12 м/с. Угол наклона плоскости к горизонту 60°.
Посмотреть РЕШЕНИЕ и ответ

Задача 14. Тележка стоит на гладких рельсах. Человек переходит с одного ее конца на другой параллельно рельсам. На какое расстояние относительно земли переместится при этом тележка? Масса человека 60 кг, масса тележки 120 кг, ее длина 6 м.
Посмотреть РЕШЕНИЕ и ответ

Задача 15. На стол поставили в вертикальном положении тонкую палочку длиной 80 см и отпустили. На сколько сантиметров сместится нижний конец палочки к тому моменту, когда она будет составлять с поверхностью стола угол 60°? Трением пренебречь.
Посмотреть РЕШЕНИЕ и ответ

Задача 16. Веревку длиной 80 см и массой 200 г положили на гладкую горизонтальную поверхность и раскрутили вокруг одного из концов с угловой скоростью 10 рад/с. Чему равна сила натяжения веревки в середине ее длины?
Посмотреть РЕШЕНИЕ и ответ

Задача 17. Два шарика массой 250г каждый, соединенные нитью длиной 1 м, движутся по гладкой горизонтальной поверхности. В некоторый момент один из шариков неподвижен, а скорость другого равна 4 м/с и направлена перпендикулярно нити. Чему равна сила натяжения нити?
Посмотреть РЕШЕНИЕ и ответ

Вы смотрели конспект по теме «Закон сохранения импульса. Задачи ЕГЭ». Ключевые слова конспекта: Определение импульса. Изменение импульса и средняя сила. Закон сохранения импульса.
Сохранение проекции импульса. Комплексные задачи. Центр масс.
Автор задач и решений: Алексей Игоревич Черноуцан. Выберите дальнейшие действия:
Источник: uchitel.pro