Положительное ускорение происходит, когда ускорение вызывает увеличение скорости объекта по величине, то есть скорость объекта увеличивается.
Давайте подробно рассмотрим эти примеры положительного ускорения.
1. Запуск ракеты:
Когда запускается ракета, требуется огромное количество топлива для выработки энергии, необходимой для разгона ракеты до очень высокой скорости. Поскольку этот процесс включает увеличение скорости ракеты, это форма положительного ускорения. Без положительного ускорения невозможно было бы запустить ракету за ракетой. Этот тип положительного ускорения является переменным, т.е. изменяется со временем.
2. Разгон автомобиля:
Транспортные средства, такие как автомобили, грузовики, велосипеды и поезда, имеют встроенные ускорители для увеличения скорости транспортного средства. Это наиболее распространенный пример положительного ускорения. В каждом автомобиле есть ускоритель, который используется для увеличения скорости. Ускорение автомобиля необходимо использовать осторожно, чтобы избежать несчастных случаев. Этот тип положительного ускорения является переменным, т.е. изменяется со временем.
СЛОМАТЬ МОЖНО ВСЁ. РЕМОНТ ЛОДКИ ПОСЛЕ ПОРОГОВ.
3. Свободно падающий объект:
Свободно падающий объект относится к объекту, который испытывает ускорение, возникающее из-за силы тяжести. Это форма положительного постоянного ускорения, т.е. оно не меняется со временем. Величина скорости, т.е. скорость падающего тела, увеличивается с постоянной скоростью по мере его движения вниз к земле. Тело достигает максимальной скорости, когда ударяется о землю.
Свободно падающий объектный опыт положительное ускорение свободного падения. положительные примеры ускорения Источник изображения: Вальоне, Gravity gravita могила, CC BY-SA 3.0 положительные примеры ускорения
4. Крутить педали на велосипеде:
Когда мы крутим педали велосипеда, мы увеличиваем его скорость. Величина увеличения скорости зависит от того, насколько быстро мы крутим педали велосипеда. В этом механическая энергия превращается в кинетическую энергия. Это также форма положительного ускорения, поскольку скорость увеличивается при вращении педалей. В этом случае ускорение является переменным, т.е. изменяется со временем.

Pезда на велосипеде для ускорения. Источник изображения: анонимные примеры положительного ускорения, Лэнс-Армстронг-TdF2004, CC BY-SA 3.0
5. Гребля на лодке:
Гребля на лодке так же, как гребля на велосипеде, увеличивает ее скорость. Величина увеличения скорости лодки зависит от того, насколько быстро мы гребем на лодке. В этом случае механическая энергия снова преобразуется в кинетическую. Это форма положительного ускорения, поскольку скорость лодки увеличивается с греблей. Здесь ускорение переменное, то есть изменяется со временем.
6. Взлет самолета:

слишком мощный и тяжёлый мотор , дельфин не могу убрать
Перед взлетом самолет совершает длительный пробег по взлетно-посадочной полосе. Во время разбега самолет увеличивает скорость для взлета. Как только скорость достигает определенного уровня, полет взлетает. Это форма положительного ускорения, которая является переменной, т.е. изменяется со временем. Без предварительного разгона самолет невозможно было бы взлететь.
Самолет бежит по взлетно-посадочной полосе перед вылетом. Пример положительного ускорения Источник изображения: Матти Блюм, Аэропорт Тегель, (IMG 9173), CC BY-SA 4.0
Это некоторые положительные примеры ускорения, с которыми мы сталкиваемся в повседневной жизни. Чтобы узнать больше о положительном ускорении, прочтите следующие параграфы.
Часто задаваемые вопросы
Что такое положительное ускорение?
Задачи «разгон» и «торможение»
При кажущемся изобилии задач на прямолинейное равноускоренное движение все они могут быть сведены к задачам двух типов. Для этого необходимо выбрать ось X таким образом, чтобы ее положительное направление совпадало с направлением движения тела. В этом случае все задачи сводятся либо к задаче «разгон» (если a > 0), либо к задаче «торможение» (если a
Задача «Разгон»
Гоночный автомобиль трогается с места, набирая скорость 30 м/с (108 км/ч) за время t = 6 с. Определите пройденный автомобилем за это время путь, считая движение автомобиля равноускоренным.
Решение.
Используем известную нам схему решения кинематических задач.
Шаг 1. Свяжем координатную ось X с дорогой, по которой разгоняется автомобиль. Начало отсчета поместим в то место, откуда автомобиль начинает разгон. Ось X направим по ходу движения автомобиля, как показано на рис. 59. В качестве единицы выберем 1 м. Включим часы (секундомер) в момент начала разгона.
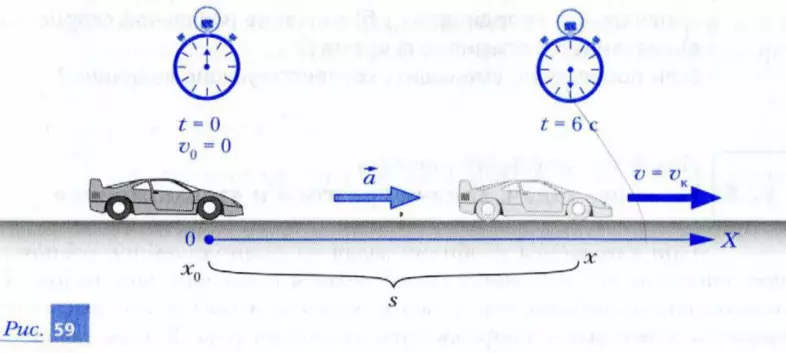
Шаг 2. Определим в выбранной нами системе отсчета начальную координату автомобиля – x0 = 0.
Шаг 3. По условию начальная скорость автомобиля v0 = 0. Так как направление ускорения совпадает с положительным направлением оси X, то значение ускорения a будет положительным.
Шаг 4. Запишем зависимость координаты от времени при прямолинейном равноускоренном движении автомобиля с учетом данных задачи:
x = x0 + v0 · t + (a · t 2 ) / 2 = 0 + 0 + (a · t 2 ) / 2 = (a · t 2 ) / 2.
Шаг 4* (новый). Запишем зависимость значения скорости автомобиля от времени:
v = v0 + a · t = 0 + a · t = a · t.
Из этого выражения видно, что при положительном значении ускорения скорость автомобиля увеличивается со временем. При этом за каждую секунду значение скорости возрастает на величину, равную a · 1 (м/с).
Шаг 5. Условие окончания разгона до скорости vк имеет вид:
Шаг 6. Объединим составленные уравнения, присвоив каждому номер и название:
x = (a · t 2 ) / 2, (1) (закон движения автомобиля)
v = a · t, (2) (зависимость скорости от времени)
v = vк. (3) (условие окончания разгона)
Шаг 7. Решение уравнений. Чтобы ответить на вопрос задачи, необходимо решить уравнение (1), подставив в него время разгона 6 с и значение ускорения a. Однако значение ускорения нам пока не известно. Зато нам известны значения начальной и конечной скоростей автомобиля. Следовательно, мы можем найти значение ускорения. Для этого в условие окончания разгона (3) подставим из уравнения (2) значение скорости a · t в момент t = 6 с:
Подставив полученное значение a в уравнение (1), находим:
x = (a · t 2 ) / 2 = (5 · 6 2 ) / 2 = 90 (м).
Ясно, что s = x — x0 = 90 — 0 = 90 (м).
Как вы заметили, в отличие от задач о равномерном движении, в шаге 4 появилось дополнение, связанное с тем, что скорость равноускоренно движущегося тела изменяется со временем. В результате появилось новое уравнение – зависимость значения скорости от времени.
Задача «Торможение»
Автобус движется со скоростью, модуль которой равен 20 м/с (72 км/ч). Водитель автобуса замечает на дороге кошку и нажимает на педаль тормоза. Определите длину тормозного пути автобуса, если модуль ускорения при торможении |a| = 4 м/с 2 .
Решение.
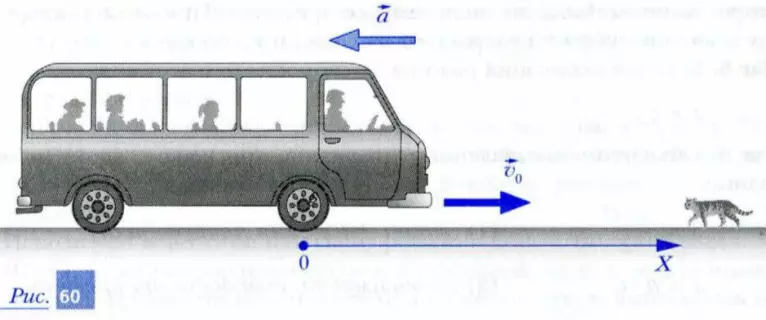
Шаг 1. Систему отсчета выберем так, как показано на рис. 60.
Шаг 2. Начальная координата автобуса x0 = 0.
Шаг 3. Значение начальной скорости автобуса v0 = 20 м/с.
Шаг 4. С учетом шагов 1, 2 и 3 зависимость координаты автобуса от времени будет иметь вид:
x = x0 + v0 · t + (a · t 2 ) / 2 = 0 + 20 · t — (4 · t 2 ) / 2.
Равноускоренное движение

Ускорение – векторная величина, оно имеет направление.
Если вектор ускорения направлен в ту же сторону, что и выбранная нами ось координат, то говорят, что проекция ускорения на ось положительная . Если же ускорение и выбранная ось направлены в разные стороны, то проекция ускорения отрицательная .
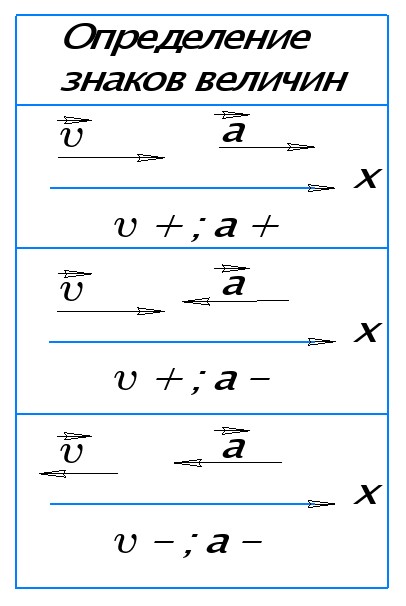
Если ускорение и скорость тела направлены в одну сторону, то модуль скорости тела увеличивается, оно разгоняется.
Если ускорение и скорость тела направлены в разные стороны, то модуль скорости тела уменьшается, тело тормозит.
Ускорение в системе СИ измеряется в м/с 2 (метрах, деленных на секунду в квадрате).
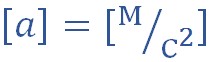
Пример. Пусть материальная точка движется вдоль оси ОХ со ускорением a = 2 м/с 2 . Это означает, что за любую секунду движения скорость тела изменяется на 2 м/с.
Равноускоренное прямолинейное движение — движение, при котором ускорение тела остается постоянным (a=const) , а скорость за равные промежутки времени изменяется на одинаковую величину.
Так как ускорение при данном виде движения остается неизменным, то скорость является линейной функцией и вычисляется по формуле:
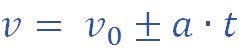
Перемещение можно рассчитать, применяя следующие формулы:
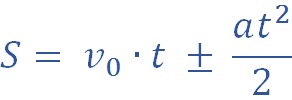
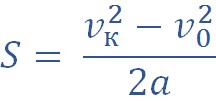
Обратим внимание, что вторую формулу удобно использовать в задачах, где не дано время движения.
Для прямолинейного равноускоренного движения закон движения выглядит следующим образом:
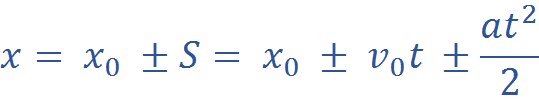
В записанных уравнениях постановка знаков ± связана со знаками проекций величин скорости, ускорения и перемещения.
Рассмотрим основные графики величин для равноускоренного прямолинейного движения.
Так как модуль ускорения при равноускоренном движении со временем не изменяется, то его график будет представлен в виде прямой линии, параллельной оси времени.
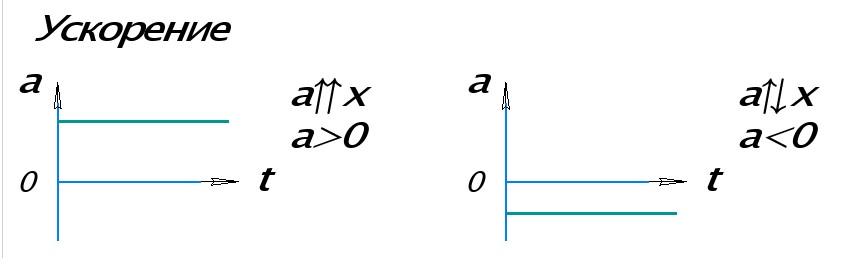
На левом рисунке проекция ускорения на ось ОХ, вдоль которой движется тело, положительная. Поэтому график ускорения лежит выше горизонтальной оси t. На правом рисунке ускорение направлено против оси ОХ, его проекция отрицательная. График лежит ниже оси t.
Так как величина скорости тела при данном виде движения рассчитывается по формуле
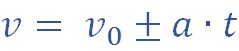
то ее график будет выглядеть как линейная функция (прямая, расположенная под углом к оси t, исходящая из точки начальной скорости).
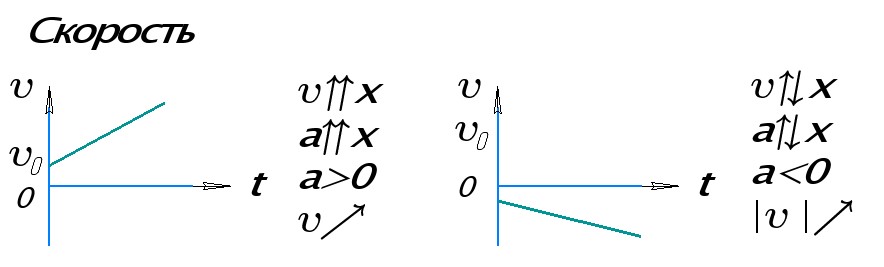
На графике слева проекция скорости положительная (υ>0), проекция ускорения тоже положительная (a>0), т.к. скорость тела возрастает со временем. График лежит выше оси t.
На графике справа тело перемещается в направлении, обратном направлению оси ОХ, поэтому проекция скорости отрицательна. Проекция ускорения тоже отрицательна (a <0), график лежит ниже оси t, тело разгоняется в направлении, противоположном оси ОХ.
График перемещения тела представляет собой ветвь параболы, исходящей из начала координат. Такой вид графика образуется из того, что формула перемещения при данном виде движения является квадратным уравнением, зависящем от t.
Так как основными видами прямолинейного движения, изучаемыми в школе, являются равномерное и равноускоренное движение, то движение, описываемое графиком в виде ветви параболы, можно сразу охарактеризовать как равноускоренное (при равномерном движении таких графиков нет ни для одной из характеризующих величин).
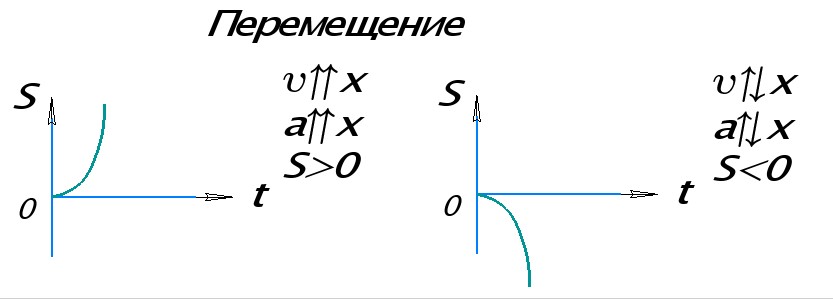
Если ветвь параболы направлена вверх на графике, значит ускорение на этом участке сонаправлено с осью ОХ. Если ветвь параболы направлена вниз, то ускорение направлено против оси ОХ.
График координаты тела представляет собой график перемещения с учетом начальной координаты x0.
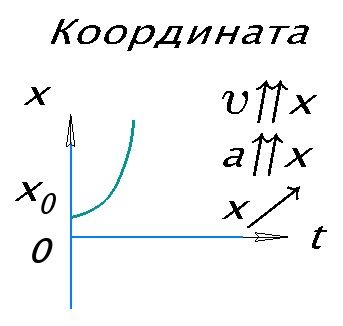
Остальные тонкости анализа графиков прямолинейного движения будут рассмотрены в отдельной главе.
Источник: www.fizika-express.ru