В своем блоге буду описывать основы технологии судоремонта, методы дефектоскопии, восстановления и упрочнения деталей, виды и методы ремонта судов и механизмов.Будет приведена технологическая документация на ремонт и изготовление деталей.
Оглавление
- Магазин
- Частные объявления
- Книги о судоремонте.
- Программное обеспечение
- Основные направления развития технологии судоремон.
Образование лопасти и ее элементы.
Лопасть образуется из винтовой поверхности, рассеченной двумя соосными цилиндрами: по диаметру винта и ступицы. Ее можно дополнительно пересечь или двумя плоскостями, перпендикулярными оси, или двумя плоскостями, проходящими через ось и расположенными под углом друг к другу. У полученного участка ВП скругляются углы, в результате чего и получается лопасть. Чтобы получить несколько лопастей винта, необходимо в качестве образующей взять крест (4 лопасти) или другую соответствующую фигуру, которая образует многозаходную винтовую поверхность.
Ваша лодка роется носом? Как правильно установить лодочный мотор по высоте?
На чертежах обычные цельнолитые винты вычерчивают в двух проекциях, на которых показывают одну лопасть и ступицу. Проекция на плоскость, перпендикулярную оси винта, называется нормальной, а на плоскость, параллельную оси винта, – боковой. Третью проекцию – горизонтальную – используют для винтов регулируемого шага или со съемными лопастями.
Поверхность лопасти, обращенная назад, называется нагнетательной (нагнетающей), а поверхность, обращенная к корпусу, – засасывающей. Когда мы говорили о типах винтовой поверхности, имелась в виду нагнетательная поверхность, а засасывающая получается путем добавления толщин к ней.
Часть лопасти, прилегающая к ступице, называется корнем, а противоположная – краем (концом) лопасти.
Передняя кромка лопасти (при работе винта на передний ход) называется входящей (ведущей), а задняя – выходящей. Входящая кромка почти всегда толще выходящей. Естественно, названия кромок не зависят от того, вращается винт на передний, на задний ход или лежит на земле.
Гребные винты, как и обычная резьба, бывают правые и левые (правого и левого вращения). Если смотреть на судно с кормы, то правый винт при работе на передний ход вращается по часовой стрелке, а левый – против часовой стрелки.
Если наблюдатель находится на ступице и смотрит на одну из лопастей, то название винта (правый или левый) совпадает с названием дальней от наблюдателя кромки, независимо от того, какой стороной лежит винт на земле. Если к винту, лежащему на земле, подойти со стороны, для определения направления вращения можно использовать «правило ноги» или «правило руки»: направление вращения совпадает с названием ноги или руки, которую удобнее поставить (положить) на лопасть. Проблемы могут возникнуть с винтами многовинтовых судов, поскольку направление вращения винтов разных бортов противоположное. Были случаи, когда после ремонта винты по ошибке меняли местами; при выходе из порта судно неожиданно начинало двигаться задним ходом вместо переднего, что приводило к авариям.
Почему транец лодки ПВХ вклеен под углом?
Форма гребных винтов довольно сложна, и две проекции дают весьма неполное представление о ней. Поэтому приходится дополнительно использовать контуры и сечения.
Развернутый контур получается, если винтовую поверхность пересечь несколькими соосными цилиндрами (разных радиусов), полученные винтовые линии развернуть на шаговые углы и соединить концы этих линий плавной кривой. Развернутый контур употребляется в некоторых странах; его недостаток в том, что длины винтовых линий искажаются. Поскольку в России эксплуатируются суда, построенные в различных странах, специалисты-судоремонтники могут встретиться с документацией, где использован развернутый контур лопасти винта. Площадь, ограниченная развернутым контуром, довольно точно соответствует площади нагнетательной поверхности лопасти.
В нашей стране применяют спрямленный контур, который получается из развернутого, если все винтовые линии вытянуть вдоль прямых, перпендикулярных оси лопасти. Этот контур принципиально точен, площадь, ограниченная спрямленным контуром, практически равна площади нагнетательной поверхности лопасти, а центр тяжести этой площади лежит на одном радиусе с центром тяжести нагнетательной поверхности лопасти.
Развернутый или спрямленный контур используется при проектировании формы лопасти гребного винта.
Введем понятие «дисковое отношение гребного винта» АЕ/Ао, где АЕ -площадь (нагнетательных поверхностей) всех лопастей; А0 – площадь диска винта.

Дисковое отношение – одна из важнейших геометрических характеристик винта.
Другая, не менее важная геометрическая характеристика – шаговое отношение P/D, равное отношению шага винта к его диаметру. Под шагом винта подразумевают шаг винтовой поверхности, по которой образована нагнетательная поверхность лопасти. Если эта поверхность аксиально-переменного шага, в качестве шага берется так называемый кромочный шаг, когда поверхность постоянного шага проводится через линию кромок (входящую и выходящую кромки, т.е. средний шаг на длине хорды профиля). У винтов радиально-переменного шага шагом считается шаг винтовой поверхности на относительном радиусе, равном 0,7 R. Дополнительно в виде таблицы или графика указывается распределение шага вдоль лопасти.
Тестирование лодочного мотора «Сельва-Пиранья» 9.9 4Т
5.2. Элементы гребного винта.
Гребные винты фиксированного шага (ВФШ) изготовляют цельными и они состоят из следующих основных элементов:
Ступицы, которая представляет собой втулку, насаживаемую на конус гребного вала;
Лопастей,радиально расположенных на ступице в количестве от 2 -х до 6 -и;
Нижняя часть лопасти, соединяющаяся с втулкой называется корнем лопастей, а верхняя часть – вершиной или концом. Передняя поверхность лопасти, обращенная в сторону корпуса судна имеет выпуклую форму и называется засасывающей, а задняя поверхность лопасти имеет вогнутую или плоскую форму и называется нагнетающей ,а пересечение этих двух плоскостей образуют кромку лопасти. (Рис 5.9.). В зависимости от типа винта применяют сегментные, авиационные и клиновидные сечения лопасти. Сечения лопастей сегментных и авиационных профилей бывают плоско-выпуклыми, двояко-выпуклыми и выпукло-вогнутыми .
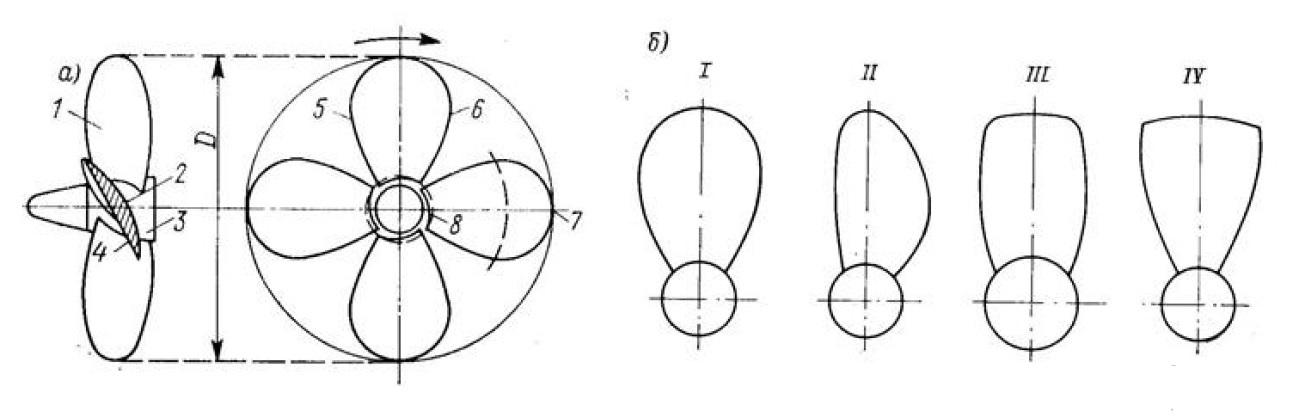
Рис. 5.9. Конструктивные элементы гребного винта (а) и
формы контуров лопастей гребных винтов (б)
/ — лопасть; 2 — засасывающая поверхность; 3 —
ступица; 4 — нагнета тельная поверхность; 5 —
выходящая кромка; 6 — входящая кромка; 7 — край
лопасти; 8 — корень лопасти. / — симметричный;
//— саблевидный; /// — ледокольный; IV —усеченный
При вращении винта поток жидкости на выпуклой засасывающей поверхности лопасти ускоряется , понижая давление (разрежение), а на нагнетающей вогнутой поверхности поток замедляется, создавая повышенное давление . В результате разности давлений создается гидродинамическая сила R, проекция которой на ось гребного винта образует упор винта Р , направленный в сторону движения судна, т.е. против силы сопротивления воды .
При равенстве сил сопротивления и упора винта R =Р – судно движется с постоянной скоростью Vp .
Исследования показали, что около 70 процентов гидродинамической силы создается за счет разрежения на засасывающей стороне лопасти. Эта сила воспринимается лопастями винта, которые через ступицу и гребной вал передают ее судну.
Поскольку лопасти имеют винтообразную поверхность, то при вращении винта вода не только отбрасывается назад, но и закручивается в сторону вращения лопастей. На закручивание потока и преодоление сопротивления вращению винта в воде затрачивается часть мощности, подводимой к винту от ГД, поэтому отношение мощности, затраченной на создание упора винта ко всей мощности, затраченной на его вращение называется к.п.д. винта и колеблется в диапазоне 0,5 ± 0,7. Для мал оборотных винтов он ближе к верхнему пределу.
5.3.Характеристики гребного винта.
При изучении работы гребных винтов используется их геометрические, кинематические и динамические характеристики.
1.Геометрическими характеристиками гребного винта являются:
-диаметр гребного винта — D
-шаг гребного винта –H –это путь, пройденный винтом за 1 оборот в твердой среде;
– шаговое отношение – это отношение шага винта к диаметру H/D
– сумма площади спрямленных лопастей – Az;
– Z –-число лопастей;
– площадь спрямленной лопасти – A;

– дисковое отношение – это отношение суммарной площади спрямленных лопастей к площади диска винта ,

где – площадь диска винта;


-отношение диаметра ступицы к диаметру винта = .
Конструкция и геометрия гребного винта. Гидродинамические характеристики гребного винта
Наибольшее распространение на кораблях и судах всех типов получил гребной винт, поэтому в дальнейшем только его и будем рассматривать.
Винт состоит из ступицы и лопастей, являющихся его рабочими элементами. За счет разницы давлений на засасывающей, обращенной в сторону движения, и нагнетающей, воспринимающей реакцию отброшенных масс воды, поверхностях лопастей создается упор гребного винта.
Лопасть — крылообразное тело, создаваемое двумя винтовыми поверхностями, линия пересечения которых называется контуром.
Как и у крыла, у лопасти различают две кромки — входящую, направленную навстречу потоку, и выходящую — противоположную первой. Граница между ними — край лопасти — самая удаленная от оси точка гребного винта. Участок, примыкающий к ступице, называется корнем лопасти.
Кратко остановимся на винтовых поверхностях, от которых самый распространенный движитель — гребной винт — получил свое название.
Заставим отрезок АВ двигаться таким образом, чтобы один его конец – точка А’-скользил по оси цилиндра, а другой – точка В – по его поверхности, одновременно вращаясь вокруг оси. Образованная таким образом поверхность носит название винтовой (рисунок 17.1).
Москва-12,5: описание мотора, технические характеристики, отзывы

Рисунок 17.1 Образование винтовой поверхности
Если скорости, поступательная и окружная, будут при этом постоянными, то образуется правильная винтовая поверхность. Точка В на боковой поверхности цилиндра опишет винтовую линию, шагом которой называется расстояние Р, проходимое этой точкой в осевом направлении за один оборот.
Рассекая винтовую поверхность соосными цилиндрами, на каждом из них получим винтовую линию – след движения соответствующей точки отрезка АВ. Следовательно, винтовую поверхность можно определить как совокупность бесконечного множества винтовых линий, описанных точками отрезка АВ. Сам этот отрезок называется образующей винтовой поверхности. Он в общем случае может быть наклонен к оси цилиндра, иметь криволинейную форму.
Разворачивая боковую поверхность цилиндра на плоскость, получим прямоугольник, в котором винтовая линия является диагональю. Нижняя половина этого прямоугольника называется шаговым треугольником: его катеты равны длине окружности и шагу винтовой линии. Если гипотенуза такого треугольника прямолинейная (рисунок 17.2,а), то винтовая линия называется винтовой линией постоянного шага, при этом шаговый угол р =const.
Криволинейная гипотенуза — признак винтовой линии переменного шага ф=f(г) , где г – угол поворота образующей относительно оси цилиндра.

Рисунок 17.2 Шаговый треугольник: а — винтовая линия постоянного шага; б — винтовая линия переменного шага
Правильная винтовая поверхность на всех радиусах в сечении имеет винтовые линии постоянного шага, кроме того соблюдается и условие Р=const. Если же поверхность образована винтовыми линиями постоянного шага, но P = f(r), то это винтовая поверхность радиально-переменного шага. Различают еще винтовую поверхность аксиально-переменного шага — шаговые треугольники имеют криволинейные гипотенузы (фconst), но один и тот же средний шаг Р = const. Если фconst и P = f(r), то такая поверхность называется винтовой поверхностью аксиально-радиально-переменного шага.
Лопасти гребных винтов образуются винтовыми поверхностями всех перечисленных типов. Так, если нагнетающая поверхность лопасти может быть правильной, то засасывающая всегда имеет в сечении винтовую линию переменного шага. Рассекая лопасть гребного винта соосным с ним цилиндром и разворачивая его на плоскость, получаем профиль сечения лопасти, шаг и шаговый угол на данном радиусе (рисунок 17.3).

Рисунок 17.3 Сечение лопасти гребного винта соосным цилиндром
Винтовая поверхность без искажений не разворачивается на плоскость. Наиболее точное представление о форме и площади лопасти дает так называемый спрямленный контур, построение которого осуществляется известными методами графики.
Основные геометрические характеристики гребного винта — число лопастей, диаметр, шаг, диаметр ступицы, форма профиля лопасти, площадь ее спрямленной поверхности. Современные гребные винты имеют диаметр до D=12м, масса такого движителя может достигать 150 т. Число лопастей винтов изменяется в пределах Zp = 28.
Наряду с диаметром гребной винт характеризуют его безразмерные геометрические характеристики. К ним относят:
- — дисковое отношение АЕ/А , где АЕ – площадь спрямленной поверхности всех лопастей; Ао — площадь диска (гидравлического сечения) гребного винта; АЕ/А = 0,21,3 (большие значения относятся к винтам быстроходных судов);
- — шаговое отношение P/D, где Р – шаг; D – диаметр винта, P/D = 0,62,0 (большие значения -винты быстроходных судов);
- — относительный диаметр ступицы dH = 0,160,35 (большие значения характерны для ВРШ и винтов со съемными лопастями).
Если относительно наблюдателя, смотрящего в корму удаляющегося судна, гребной винт вращается по часовой стрелке, то его называют винтом правого вращения, в противном случае– винтом левого вращения.
Гидродинамические характеристики гребного винта. Кинематика гребного винта. В процессе работы гребной винт с частотой n вращается вокруг своей оси и с поступательной скоростью vA перемещается вдоль нее. Путь, проходимый винтом в осевом направлении за один оборот, называется поступью

Разница между шагом гребного винта и его поступью называется скольжением.
Для конкретного гребного винта (Р=const) поступь однозначно определяет скольжение, обе эти величины изменяются в широких пределах, что позволяет винту выполнять функции движителя при всех скоростях движения судна.
Перейдя к безразмерной величине, запишем относительную поступь в виде

Относительная поступь J – важнейшая кинематическая характеристика гребного винта, определяющая режим его работы, а следовательно и силы на нем возникающие.
Кривые действия гребного винта. Работая в качестве движителя, гребной винт создает вызванные осевые скорости. Вращаясь вокруг своей оси, он вовлекает в это движение окружающую жидкость, закручивает поток, т. е. создает еще и вызванные окружные скорости. На это затрачивается дополнительная мощность, что является одной из причин, почему КПД винта меньше, чем у идеального движителя. Кроме того, вызванные окружные скорости изменяют и характер обтекания лопасти.
Источник: seaofthievesrus.ru
Конструкция и геометрия гребного винта. Гидродинамические характеристики гребного винта
Наибольшее распространение на кораблях и судах всех типов получил гребной винт, поэтому в дальнейшем только его и будем рассматривать.
Винт состоит из ступицы и лопастей, являющихся его рабочими элементами. За счет разницы давлений на засасывающей, обращенной в сторону движения, и нагнетающей, воспринимающей реакцию отброшенных масс воды, поверхностях лопастей создается упор гребного винта.
Лопасть — крылообразное тело, создаваемое двумя винтовыми поверхностями, линия пересечения которых называется контуром.
Как и у крыла, у лопасти различают две кромки — входящую, направленную навстречу потоку, и выходящую — противоположную первой. Граница между ними — край лопасти — самая удаленная от оси точка гребного винта. Участок, примыкающий к ступице, называется корнем лопасти.
Кратко остановимся на винтовых поверхностях, от которых самый распространенный движитель — гребной винт — получил свое название.
Заставим отрезок АВ двигаться таким образом, чтобы один его конец — точка А’-скользил по оси цилиндра, а другой — точка В — по его поверхности, одновременно вращаясь вокруг оси. Образованная таким образом поверхность носит название винтовой (рисунок 17.1).
Рисунок 17.1 Образование винтовой поверхности
Если скорости, поступательная и окружная, будут при этом постоянными, то образуется правильная винтовая поверхность. Точка В на боковой поверхности цилиндра опишет винтовую линию, шагом которой называется расстояние Р, проходимое этой точкой в осевом направлении за один оборот.
Рассекая винтовую поверхность соосными цилиндрами, на каждом из них получим винтовую линию — след движения соответствующей точки отрезка АВ. Следовательно, винтовую поверхность можно определить как совокупность бесконечного множества винтовых линий, описанных точками отрезка АВ. Сам этот отрезок называется образующей винтовой поверхности. Он в общем случае может быть наклонен к оси цилиндра, иметь криволинейную форму.
Разворачивая боковую поверхность цилиндра на плоскость, получим прямоугольник, в котором винтовая линия является диагональю. Нижняя половина этого прямоугольника называется шаговым треугольником: его катеты равны длине окружности и шагу винтовой линии. Если гипотенуза такого треугольника прямолинейная (рисунок 17.2,а), то винтовая линия называется винтовой линией постоянного шага, при этом шаговый угол р =const.
Криволинейная гипотенуза — признак винтовой линии переменного шага ф=f(г) , где г — угол поворота образующей относительно оси цилиндра.

Рисунок 17.2 Шаговый треугольник: а — винтовая линия постоянного шага; б — винтовая линия переменного шага
Правильная винтовая поверхность на всех радиусах в сечении имеет винтовые линии постоянного шага, кроме того соблюдается и условие Р=const. Если же поверхность образована винтовыми линиями постоянного шага, но P = f(r), то это винтовая поверхность радиально-переменного шага. Различают еще винтовую поверхность аксиально-переменного шага — шаговые треугольники имеют криволинейные гипотенузы (фconst), но один и тот же средний шаг Р = const. Если фconst и P = f(r), то такая поверхность называется винтовой поверхностью аксиально-радиально-переменного шага.
Лопасти гребных винтов образуются винтовыми поверхностями всех перечисленных типов. Так, если нагнетающая поверхность лопасти может быть правильной, то засасывающая всегда имеет в сечении винтовую линию переменного шага. Рассекая лопасть гребного винта соосным с ним цилиндром и разворачивая его на плоскость, получаем профиль сечения лопасти, шаг и шаговый угол на данном радиусе (рисунок 17.3).

Рисунок 17.3 Сечение лопасти гребного винта соосным цилиндром
Винтовая поверхность без искажений не разворачивается на плоскость. Наиболее точное представление о форме и площади лопасти дает так называемый спрямленный контур, построение которого осуществляется известными методами графики.
Основные геометрические характеристики гребного винта — число лопастей, диаметр, шаг, диаметр ступицы, форма профиля лопасти, площадь ее спрямленной поверхности. Современные гребные винты имеют диаметр до D=12м, масса такого движителя может достигать 150 т. Число лопастей винтов изменяется в пределах Zp = 28.
Наряду с диаметром гребной винт характеризуют его безразмерные геометрические характеристики. К ним относят:
- — дисковое отношение АЕ/А0, где АЕ — площадь спрямленной поверхности всех лопастей; Ао — площадь диска (гидравлического сечения) гребного винта; АЕ/А0 = 0,21,3 (большие значения относятся к винтам быстроходных судов);
- — шаговое отношение P/D, где Р — шаг; D — диаметр винта, P/D = 0,62,0 (большие значения -винты быстроходных судов);
- — относительный диаметр ступицы dH = 0,160,35 (большие значения характерны для ВРШ и винтов со съемными лопастями).
Если относительно наблюдателя, смотрящего в корму удаляющегося судна, гребной винт вращается по часовой стрелке, то его называют винтом правого вращения, в противном случае— винтом левого вращения.
Гидродинамические характеристики гребного винта. Кинематика гребного винта. В процессе работы гребной винт с частотой n вращается вокруг своей оси и с поступательной скоростью vA перемещается вдоль нее. Путь, проходимый винтом в осевом направлении за один оборот, называется поступью

Разница между шагом гребного винта и его поступью называется скольжением.
Для конкретного гребного винта (Р=const) поступь однозначно определяет скольжение, обе эти величины изменяются в широких пределах, что позволяет винту выполнять функции движителя при всех скоростях движения судна.
Перейдя к безразмерной величине, запишем относительную поступь в виде

Относительная поступь J — важнейшая кинематическая характеристика гребного винта, определяющая режим его работы, а следовательно и силы на нем возникающие.
Кривые действия гребного винта. Работая в качестве движителя, гребной винт создает вызванные осевые скорости. Вращаясь вокруг своей оси, он вовлекает в это движение окружающую жидкость, закручивает поток, т. е. создает еще и вызванные окружные скорости. На это затрачивается дополнительная мощность, что является одной из причин, почему КПД винта меньше, чем у идеального движителя. Кроме того, вызванные окружные скорости изменяют и характер обтекания лопасти.
Если рассечь гребной винт двумя соосными цилиндрами, радиусы которых г и г + dr, то заключенный между ними участок лопасти можно рассматривать как элемент несущего крыла. Результирующая скорость vR обтекания этого элемента — геометрическая сумма четырех скоростей: осевой хА окружной Щr и двух вызванных, тех же наименований wX0 и wИ0. В теории идеального движителя было доказано, что вызванная осевая скорость в диске движителя равна половине таковой на бесконечности. То же соотношение справедливо и для вызванных окружных скоростей, т. е. wИ0 = wИ/2.
Винт закручивает поток в сторону своего вращения, поэтому относительная окружная скорость элемента лопасти составляет (Щr — wИ0), а для результирующей скорости будет справедливым выражение

Рассмотрим обтекание элемента лопасти, протяженностью сСг в обращенном движении, т.е. мысленно остановим винт, а всем скоростям придадим противоположное направление (рисунок 17.4).

Рисунок 17.4 Схема обтекания элемента лопасти гребного винта
Элемент лопасти, обтекается потоком со скоростью хR под углом атаки
где ф -шаговый угол, вi — угол индуктивной поступи, определяемый выражением

Элемент лопасти — элемент несущего крыла, на нем возникают подъемная сила dY и сопротивление dX:


где bdr — площадь элемента в плане; b(r) — хорда крыла.
Назначение гребного винта как движителя создавать упор T — силу, направленную вдоль оси в сторону движения. Для преодоления момента сопротивления вращению Q к винту необходимо подвести мощность
Проектируя элементарные подъемную силу и силу профильного сопротивления на интересующие нас направления (рисунок 17.4), получаем элементарный упор
dT = dY cos вi — dX sin вi = dY cos вi (l -е· tg вi ) (17.10)
и элементарную силу сопротивления вращению
dr = dY sin вi + dX cos вi = dY sin вi (l+-е· ctg вi ) (17.11)
где е = Сх/Су — обратное качество профиля.
Сопоставляя (17.10) и (17.11), убеждаемся, что наличие вязкости жидкости (е>0) приводит к уменьшению полезной силы — упора — и к увеличению момента сопротивления вращению dQ = rdф, т. е. к снижению эффективности гребного винта (его КПД).
Интегрируя (17.10) и (17.11) вдоль всей лопасти, с учетом (17.8) найдем создаваемый гребным винтом упор Т и момент Q, необходимый для его вращения:

где Zр — число лопастей; гн, Р. — радиусы ступицы и винта соответственно. Приведем подынтегральные выражения к безразмерному виду



где -относительный радиус; — безразмерная ширина лопасти

Анализ выражений (17.13) позволяет сделать вывод, что силы, возникающие на гребном винте, являются сложными функциями его размеров и формы контура лопастей формы профиля (Су) сечения лопасти, его угла атаки [вi,ц- см. (17.6)], относительной поступи — и вызванных скоростей—(17.4), (17.7).
Назвав безразмерные интегралы в (17.13) коэффициентами упора Кт и момента КQ соответственно, запишем

Эффективность работы гребного винта, как любого преобразователя энергии, определяется его КПД — отношением полезной ТvA и затраченной QЩ мощностей:

и зависит не только от сил, действующих на винте (Кт, КQ, но и режима его работы J.
Для анализа потерь энергии, сопровождающих работу гребного винта, запишем КПД элемента лопасти

где зrx- осевой; зrИ — окружной и згс — конструктивный КПД элемента
Как следует из (17.16), каждый из коэффициентов учитывает определенный вид потерь: зrx — на создание вызванных осевых, зrИ — вызванных окружных скоростей, згс -вязкостные потери.
Произведение первых двух коэффициентов характеризует потери энергии на создание вызванных (индуцированных) скоростей и называется индуктивным КПД элемента:
Для гребного винта в целом имеют место дополнительные потери, не фигурирующие в (17.16). Это, во-первых, концевые потери, возникающие за счет перетекания жидкости у края лопасти— аналог индуктивных потерь у крыла конечного удлинения, во-вторых, КПД винта снижает ступица, которая не создает упора, но потребляет мощность на преодоление сопротивления вращению. Тем не менее выражение (17.17) может быть распространено на винт в целом. При этом потери энергии на ступицу относят к конструктивным, а на концевые вихри — к индуктивным.
Силы, создаваемые гребным винтом, определяются режимом работы, т. е. его поступью. Зависимости упора и момента от поступи (рисунок 17.6) принято называть кривыми действия гребного винта. Углы атаки элементов лопасти имеют максимальные значения при отсутствии осевой скорости (см. рисунок 17.5), т. е. в так называемом швартовном режиме, когда hа = 0. При этом достигают максимума и значения упора и момента. С ростом скорости vа увеличивается hа и уменьшается угол атаки; соответственно снижаются и действующие на лопасть силы.
Поступь Р1, при которой упор обращается в нуль, называется гидродинамическим шагом гребного винта или поступью (шагом) нулевого упора. В случае, когда Q =0, имеет место поступь (шаг) нулевого момента Р2. Разница между ними m=Р2 -Р1 — параль в определенной степени — характеризует эффективность движителя; чем меньше параль, тем совершеннее гребной винт. В идеальной жидкости теоретически m=0. Как правило, имеет место соотношение Р < Р1 т. е. при равенстве поступи геометрическому шагу винта hа = Р упор Т > 0. Это объясняется тем, что за счет конечной стрелки пробига ус, угол нулевой подъемной силы бо> 0 (см. рисунок 16.7).
В диапазоне поступей 0 < hA < P1 винт создает упор (Т > 0) и для своего вращения требует затраты мощности (Q > 0, PD = QЩ > 0), т. е. выполняет функции движителя. При hA>Р2 и упор и момент отрицательны — гребной винт, вращаемый набегающим потоком, создает сопротивление движению, однако с него, как с турбины, можно снимать энергию. Соответственно, этот режим работы винта называют турбинным.
В случае, когда P1< hA< Р2 говорят, что винт парализован: для его вращения надо подвести энергию, а упор он создает при этом отрицательный. Расчетный режим работы гребного винта — в диапазоне поступей 0 < hA < P1. В процессе эксплуатации могут, однако, иметь место и режимы, когда hA > P1 — при реверсе судна, при его буксировке, при движении под парусами с неработающим двигателем, для многовальной установки, когда работает только часть гребных винтов.
Кривые действия (рисунок 17.5) характеризуют работу конкретного гребного винта (D, P, Zp и др.) при конкретной (hA=const) частоте вращения. Изменение последней приведет к изменению Т и Q при hA = const. Такая неоднозначность, а кроме того, и зависимость динамических характеристик гребного винта от размеров существенно затрудняют использование кривых действия в приведенном выше виде.
Рисунок 17.5 Кривые действия гребного винта
Рисунок 17.6 ГДХ гребного винта
Представив упор и момент в безразмерном виде с помощью зависимостей (17.14) и в функции от относительной поступи, получим гидродинамические характеристики (ГДХ) гребного винта (рисунок 17.6). Сюда же обычно наносят и зависимость зо(J) — КПД обращается в нуль при J = 0 и J=Р1/D [см. (17.15)]: в первом случае отсутствует скорость (vA=0), во втором упор (Т = 0).
В соответствии с известной из высшей математики теоремой Ролля между этими двумя точками имеет место экстремум — максимальное значение КПД. Проектируя гребной винт, стремятся, чтобы он работал именно в этой области. Представленные в безразмерном виде ГДХ одинаковы для всех геометрически подобных гребных винтов. Режим работы — относительная поступь — однозначно определяет коэффициенты упора и момента, а вместе с ними и КПД. Независимыми на рисунке 17.6 являются только Кт и КQ, з0 определяется с помощью (17.15).
Источник: www.studwood.net
Инженерная методика определения упора гребного винта Текст научной статьи по специальности «Механика и машиностроение»
Аннотация научной статьи по механике и машиностроению, автор научной работы — Проскурина Наталия Борисовна, Сенюшкин Николай Сергеевич, Суханов Андрей Владимирович, Ямалиев Руслан Рафаилович
Рассматриваются вопросы формирования инженерной методики для расчета энергетических характеристик двигателя. Приведен расчет основных параметров гребного винта и двигателя по основным характеристикам судна.
i Надоели баннеры? Вы всегда можете отключить рекламу.
Похожие темы научных работ по механике и машиностроению , автор научной работы — Проскурина Наталия Борисовна, Сенюшкин Николай Сергеевич, Суханов Андрей Владимирович, Ямалиев Руслан Рафаилович
Модель движения судна в горизонтальной плоскости
Модель движения судна в горизонтальной плоскости
Сужение области расчетных значений главных размерений ледоколов из условия оптимального использования гребных винтов
Оптимизация основных элементов и формы корпуса ледокола в зависимости от ледовых условий
Винты изменяемого шага: основные результаты и направление исследований
i Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
i Надоели баннеры?
Вы всегда можете отключить рекламу.
Engineering computation methods for marine screw propeller
This article observes questions of an engineering technique formation for calculation of engine power characteristics. It includes calculation of main parameters for marine screw propeller and engine regarding basic watercraft characteristics.
Текст научной работы на тему «Инженерная методика определения упора гребного винта»
Н. Б. Проскурина, Н. С. Сенюшкин, А. В. Суханов, Р. Р. Ямалиев
ИНЖЕНЕРНАЯ МЕТОДИКА ОПРЕДЕЛЕНИЯ УПОРА ГРЕБНОГО ВИНТА
Рассматриваются вопросы формирования инженерной методики для расчета энергетических характеристик двигателя. Приведен расчет основных параметров гребного винта и двигателя по основным характеристикам судна. Судовые газотурбинные двигатели; судовые движители; гребной винт; упор гребного винта
В настоящее время в связи с возросшей потребностью в проектировании судов различных классов возникает необходимость формирования инженерной методики для расчета энергетических характеристик двигателя. Особое место занимает этап предварительного проектирования. Он характеризуется ограниченностью исходных данных для расчета разрабатываемых узлов. На данном этапе необходимо определить тип и основные характеристики движителя, в том числе потребную мощность главной силовой установки в первом приближении для обеспечения необходимой скорости судна.
Диаметр и шаг винта являются важнейшими параметрами, от которых зависит степень использования мощности двигателя, а следовательно, и возможность достижения наибольшей скорости хода судна. При движении корпус судна увлекает за собой воду, создавая попутный поток, поэтому действительная скорость встречи винта с водой УА всегда несколько меньше, чем фактическая скорость судна У. У быстроходных глиссирующих мотолодок разница невелика — всего 2-5%, так как их корпус скользит по воде и почти не «тянет» ее за собой. У катеров, идущих со средней скоростью хода, эта разница составляет 5-8%, а у тихоходных глубокосидящих катеров достигает 15-20%.
В свою очередь и корпус судна, образуя попутный поток, уменьшает скорость потока воды, натекающей на гребной винт. Это учитывает коэффициент попутного потока w.
Скорость натекания воды на винт рассчитывается по формуле
У — скорость судна;
Величина, называемая скольжением, обуславливает работу лопасти винта под углом атаки а к потоку воды. Отношение скольжения
к теоретическом скорости винта в процентах называется относительным скольжением (2)
где п — частота вращения винта.
Оптимальная величина скольжения для винтов, имеющих шаговое отношение Н / В < 1,2, составляет 5 = 0,14-0,16; для винтов, имеющих Н / В >1,2, 5 = 0,12-0,14. При выборе шагового отношения НЮ можно руководствоваться следующими рекомендациями. Для легких быстроходных лодок требуются винты с большим шагом или шаговым отношением Н/В, для тяжелых и тихоходных — с меньшим. При обычно применяемых двигателях с номинальной частотой вращения 1500-5000 об ./мин. оптимальное шаговое отношение Н/В составляет: для гоночных мотолодок и глиссеров — 0,9-1,5; легких прогулочных катеров — 0,8-1,2; водоизмещаю-щих катеров — 0,6^3-1,0 и очень тяжелых тихоходных катеров — 0,55^0,80. Следует иметь в виду, что эти значения справедливы, если гребной вал делает примерно 1000 об ./мин. из расчета на каждые 15 км/ч скорости лодки; при иной частоте вращения вала необходимо применять редуктор.
Гребной винт (рис. 1) преобразует вращение вала двигателя в упор — силу, толкающую судно вперед. При вращении винта на поверхностях его лопастей, обращенных вперед — в сторону движения судна (засасывающих), создается разрежение, а на обращенных назад (нагнетающих) — повышенное давление воды. В результате разности давлений на лопастях возникает сила У (ее называют подъемной). Разложив силу на составляющие — одну, направленную в сторону движения судна, а вторую перпендикулярно к нему, получим силу Р, создающую упор гребного винта, и силу Т, образующую крутящий момент, который преодолевается двигателем.
Контактная информация: (347) 273-36-77
Рис. 1. Схема сил и скоростей на лопасти винта (правого вращения)
На рис. 1 показаны силы и скорости, действующие в каком-то одном определенном поперечном сечении лопасти, расположенном на каком-то определенном радиусе г гребного винта. Окружная скорость вращения Уг зависит от радиуса, на котором сечение расположено (Уг = 2лгп, где п — частота вращения винта, об/с). Скорость поступательного движения винта Уа остается постоянной для любого сечения лопасти. Таким образом, чем больше г, т. е. чем ближе расположен рассматриваемый участок к концу лопасти, тем больше окружная скорость Уг, а следовательно, и суммарная скорость Ж.
Так как сторона Уа в треугольнике рассматриваемых скоростей остается постоянной, то по мере удаления сечения лопасти от центра необходимо разворачивать лопасти под большим углом к оси винта, чтобы а сохранял оптимальную величину, т. е. оставался одинаковым для всех сечений. Таким образом, получается винтовая поверхность с постоянным шагом Н. Напомним, что шагом винта называется перемещение любой точки лопасти вдоль оси за один полный оборот винта.
Представить сложную винтовую поверхность лопасти помогает рис. 2. Лопасть при работе винта как бы скользит по направляющим угольникам, имеющим на каждом радиусе разную длину основания, но одинаковую высоту -шаг Н, и поднимается за один оборот на величину Н. Произведение же шага на частоту вращения представляет собой теоретическую скорость перемещения винта вдоль оси.
Упор в большой степени зависит от угла атаки а профиля лопасти. Оптимальное значение а для быстроходных катерных винтов 4-8°. Если а больше оптимальной величины, то мощность двигателя непроизводительно затрачивается на преодоление большого крутящего момента; если же угол атаки мал, подъемная сила и, следовательно, упор Р будут невелики, мощность двигателя окажется недоиспользованной.
Рис. 2. Винтовая поверхность лопасти (а) и шаговые угольники (б)
На схеме, иллюстрирующей характер взаимодействия лопасти и воды, а можно представить как угол между направлением вектора скорости набегающего на лопасть потока Ж и нагнетающей поверхностью. Вектор скорости потока Ж образован геометрическим сложением векторов скорости поступательного перемещения Уа винта вместе с судном и скорости вращения Уг, т. е. скорости перемещения лопасти в плоскости, перпендикулярной оси винта.
Сопротивление корпуса судна [1] рассчитывается по формуле (3):
где р = 1025 кг/м3 — плотность воды, £ — коэффициент полного сопротивления, О — суммарная смоченная поверхность, м2.
Сопротивление корпуса судна зависит от его формы. Для описания формы корпуса судна существует ряд коэффициентов, значение которых влияет на ходовые параметры судна (рис. 3).
Коэффициент полноты конструктивной ватерлинии а — отношение площади конструктивной ватерлинии (КВЛ) к площади прямоугольника, стороны которого равны Ь и В. Чем меньше этот коэффициент, тем острее ватерлиния. Обычно суда с большим Ь/В (длинные узкие суда) имеют большие коэффициенты полноты КВЛ, чем короткие широкие суда.
Коэффициент полноты мидель-шпангоута в — отношение погруженной площади мидель-шпангоута к площади прямоугольника со сторонами В и Т. На него существенное влияние оказывает форма шпангоутов, а также подъем и радиус скулы. Чем больше подъем и радиус скулы (например, у малых рыболовных судов,
буксиров и ледоколов), тем меньше коэффициент полноты мидель-шпангоута.
Коэффициент общей полноты 5 — отношение объема подводной части судна к объему тела со сторонами Ь, В, Т. Этот коэффициент до некоторой степени характеризует форму судна в отношении остроты и оказывает существенное влияние на водоизмещение (грузоподъемность); с другой стороны, с ростом 5 увеличивается сопротивление судна. Напротив, судно при заданном водоизмещении с уменьшением коэффициента полноты становится длиннее, не становясь при этом тяжелее, так как потребная мощность двигателя при заданной скорости уменьшается, вследствие чего потребность в топливе становится меньше. Такое судно будет более рентабельным еще и потому, что оно длиннее и, следовательно, может иметь больше трюмов.
Коэффициент продольной полноты ф — отношение водоизмещения к объему тела, основанием которого служит площадь мидель-шпангоута, а высотой — длина судна. Этот коэффициент всегда немного больше, чем коэффициент общей полноты, и лучше характеризует остроту оконечностей судна. Большой коэффициент полноты мидель-шпангоута означает полные оконечности судна, небольшой — напротив, узкие. Однако при сравнении двух судов всегда нужно учитывать отношение Ь/В.
Рис. 3. Коэффициенты полноты ватерлинии и общей полноты: 1 — площадь КВЛ,
В — ширина судна, КВЛ — конструктивная ватерлиния, Ь — длина судна, Т — осадка судна, 1 — подъем скулы, 2 — площадь мидель-шпангоута, 3 — радиус закругления скулы, В — ширина судна
При больших Ь/В (длинные узкие суда) коэффициенты полноты мидель-шпангоута или общей полноты могут быть больше, чем при малом Ь/В (короткие широкие суда); при этом обводы не становятся полнее.
Указанные выше коэффициенты полноты взаимосвязаны, поэтому их нельзя выбирать произвольно. Перечисленные характеристики
формы (относительные величины и коэффициенты полноты) во многом определяют поведение судна в море, сопротивление движению и рентабельность судов и, кроме того, взаимно влияют друг на друга [2].
Полезная мощность, развиваемая винтом, рассчитывается по формуле (4)
где РЕ — упор винта,
V — коэффициент попутного потока,
t — коэффициент засасывания
Упор винта РЕ рассчитывается по формуле
Каждый двигатель имеет свою так называемую внешнюю характеристику — зависимость снимаемой с вала мощности от частоты вращения коленчатого вала при полностью открытом дросселе карбюратора. Такая характеристика для подвесного мотора «Вихрь», например, показана на рис. 4 (кривая 1). Максимум мощности в 21,5 л.с. двигатель развивает при 5000 об./мин.
Мощность, которая поглощается на данной лодке гребным винтом в зависимости от частоты вращения мотора, показана на рис. 4 не одной, а тремя кривыми — винтовыми характеристиками 2, З и 4, каждая из которых соответствует определенному гребному винту, т. е. винту определенного шага и диаметра.
При увеличении и шага, и диаметра винта выше оптимальных значений лопасти захватывают и отбрасывают назад слишком большое количество воды: упор при этом возрастает, но одновременно увеличивается и потребный крутящий момент на гребном валу.
Винтовая характеристика 2 такого винта пересекается с внешней характеристикой двигателя 1 в точке А. Это означает, что двигатель уже достиг предельного — максимального значения крутящего момента и не в состоянии проворачивать гребной винт с большой частотой вращения, т. е. не развивает номинальную частоту вращения и соответствующую ей номинальную мощность. В данном случае положение точки А показывает, что двигатель отдает всего 12 л.с. мощности вместо 22 л.с. Такой гребной винт называется гидродинамически тяжелым.
Наоборот, если шаг или диаметр винта малы (кривая 4), и упор, и потребный крутящий момент будут меньше, поэтому двигатель не только легко разовьет, но и превысит значение но-
минальной частоты вращения коленвала. Режим его работы будет характеризоваться точкой С. И в этом случае мощность двигателя будет использоваться не полностью, а работа на слишком высоких оборотах сопряжена с опасно большим износом деталей. При этом надо подчеркнуть, что поскольку упор винта невелик, судно не достигнет максимально возможной скорости. Такой винт называется гидродинамически легким [3].
Рис. 4. Внешняя и винтовая характеристики мотора «Вихрь»
Для каждого конкретного сочетания судна и двигателя существует оптимальный гребной винт. Для рассматриваемого примера такой оптимальный винт имеет характеристику 3, которая пересекается с внешней характеристикой двигателя в точке В, соответствующей его максимальной мощности. Рис.
5 иллюстрирует важность правильного подбора винта на примере мотолодки «Крым» с подвесным мотором «Вихрь». При использовании штатного винта мотора с шагом 300 мм мотолодка с 2 чел. на борту развивает скорость 37 км/ч. С полной нагрузкой 4 чел. скорость лодки снижается до 22 км/ч. При замене винта другим с шагом 264 мм скорость с полной нагрузкой повышается до 32 км/ч. Оптимальные же результаты достигаются с гребным винтом, имеющим шаговое отношение H/D = 1,0 (шаг и диаметр равны 240 мм): максимальная скорость повышается до
40-42 км/ч, скорость с полной нагрузкой — до 38 км/ч. Несложно сделать вывод и о существенной экономии горючего, которую можно получить с винтом уменьшенного шага. Если со штатным винтом при нагрузке 400 кг расходуется 400 г горючего на каждый пройденный километр пути, то при установке винта с шагом 240 мм расход горючего составит 237 г/км.
При движении у носа и кормы судна создаются волны, которые с увеличением скорости становятся больше. Это объясняется тем, что с увеличением скорости движения в кормовой части судна возникает значительное разрежение, а в носовой — зона повышенного давления. Энергия, израсходованная на образование волн, является волновым сопротивлением, величина которого определяется скоростью и длиной судна. При движении у носа и кормы судна создаются волны, которые с увеличением скорости становятся больше.
200 Ж т 500 Нащт, хг
Рис. 5. Зависимость скорости мотолодки «Крым» от нагрузки и шага гребного винта мотора «Вихрь» мощностью 14,8 кВт (20 л.с.)
Характеристикой волнового сопротивления судна является отношение скорости к длине, называемое числом Фруда (6):
Эта характеристика позволяет сравнивать суда различных размеров, что дает возможность определить сопротивление и тем самым мощность двигателя для строящегося судна с помощью буксировочных испытаний моделей. Скорости судна и модели соотносятся как квадратные корни из их линейных размеров (7):
г судна * модели (7)
Это означает, например, что строящемуся судну длиной 130 м, шириной 14 м с осадкой 6,6 м, с водоизмещением 5900 т и скоростью 25 уз (12,86 м/с) соответствует скорость модели 2,572 м/с при длине ее 5,2 м. При этой скорости у модели возникает волнообразование, которое геометрически подобно волнообразованию натурного судна. Измеренное при этом сопротивление содержит, однако, не только волновое сопротивление, но и еще один компонент — сопротивление трения, которое возникает вследствие тормозящего действия воды, протекающей мимо корпуса.
Сопротивление трения зависит от площади смоченной поверхности корпуса, от ее качества (степени шероховатости) и от скорости. Его можно рассчитать с достаточной точностью по опытным данным как для модели, так и для судна. Если полное сопротивление модели уменьшить на расчетный коэффициент трения, получится волновое сопротивление модели.
При пересчете действует положение, что волновые сопротивления двух геометрических подобных тел — судна и модели — соотносятся как их водоизмещения. Но это простое соотношение справедливо только тогда, когда судно и модель движутся со сравнимыми скоростями, так что возникают геометрически подобные волнообразования.
Если к волновому сопротивлению (определенному опытами на модели) прибавить расчетное сопротивление трения, получится полное сопротивление судна. В нашем примере при модельных испытаниях было определено волновое сопротивление в 0,31 МН и путем расчета — сопротивление трения в 0,35 МН. Полное сопротивление судна составляет, таким образом, 0,66 МН. Разумеется, при окончательном определении потребной мощности двигателей нужно учитывать также воздушное и вихревое сопротивления [3].
Доля волнового сопротивления и сопротивления трения в полном сопротивлении зависит
от формы судна и его скорости. У больших тихоходных судов волновое сопротивление составляет примерно 20%, а у очень быстроходных — до 70% полного сопротивления.
1. Войткунский Я. И. Сопротивление движению судов: Учеб. Л.: Судостроение, 1988. 288 с.
2. Морской сайт [Электронный ресурс]. [2009]
иКЬ: http://www.seaman-sea.ru (дата обращения
3. Устройство и принцип работы гребного винта [Электронный ресурс]. [2009] ИКЬ: http://www. motolodka.ru/ (дата обращения: 4.10.2010).
Проскурина Наталия Борисовна, магистрант каф. авиац. двигателей. Дипл. бакалавр техники и технологии (УГАТУ, 2009). Иссл. в обл. процессов в центробежных компрессорах ГТД с использованием имитац. и 3Б-числ. моделирования.
Сенюшкин Николай Сергеевич, доц. каф. авиац. теплотехники и теплоэнергетики, зам. декана ФАД. Дипл. инж. по авиац. двигателям и энер. уст. (УГАТУ, 2005). Канд. техн. наук по тепл., электро-ракент. двигателям и энергоустановкам летательн. аппаратов (УГАТУ, 2009). Иссл. в обл. судостроения, проектир. БПЛА и систем упр-я, моделир-я и проектирования камер сгорания авиац.
ГТД.
Суханов Андрей Владимирович, магистрант каф. авиац. двигателей. Иссл. в обл. автоматизации процесса испытаний авиационных ГТД.
Ямалиев Руслан Рафаилович, мл. науч. сотр. НИЛ САПР-Д. Дипл. инж.-констр. (УГАТУ, 2004). Иссл. в обл. автоматизации испытаний ГТД и проектирования БПЛА.
Источник: cyberleninka.ru