Олимпиадная задачка для старшеклассников. Но справитесь ли с ней вы?
Это кавер-версия задачи про волка, козу и капусту — классическую задачу на алгоритмическое мышление. Она очень простая для разработчиков, и если вы можете решить её с первого раза, можете гордиться собой — только 1 человек из 10 решает эту задачу правильно с первого раза.
Зачем уметь решать такие задачи: помогает в составлении сортировочных алгоритмов и успешно проходить собеседования в ИТ-компаниях. Также важно уметь обосновывать свой ход мыслей.
Ситуация. На одном берегу реки находятся шесть человек: три гопника и три философа. Пока что они ведут непринужденные беседы об экзистенциальном, но все они должны будут рано или поздно оказаться на другом берегу.
Есть одна лодка, в которую могут поместиться только два человека, но философы управлять лодкой не умеют, а гопники умеют. Также нельзя оставлять на одном берегу философов больше, чем гопников, потому что тогда философы взорвут мозг гопникам разговорами о природе вещей. Как переправить всех через реку?
Уроки Scratch. Загадка о Волке, Козе и Капусте
Для первой поездки есть пять вариантов:
- один гопник — не подходит, потому что на берегу философов становится больше и они взорвут мозг;
- два гопника — не подходит по той же причине;
- один или два философа — тоже нет, потому что они не умеют управлять лодкой;
- философ и гопник — единственный вариант, который остаётся.
Значит, первым рейсом пара «философ-гопник» отправляется на другой берег:
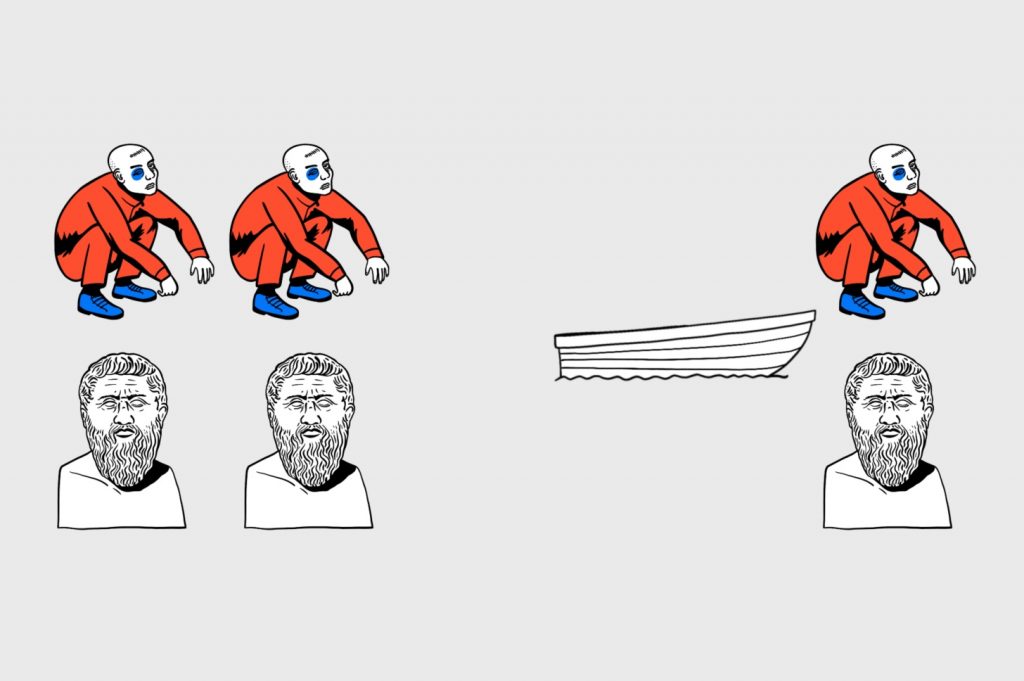
Теперь лодку надо как-то отправить назад. Но так как философ не умеет ей управлять, то он остаётся на берегу, а гопник — возвращается. Философы не взрывают никому мозг:
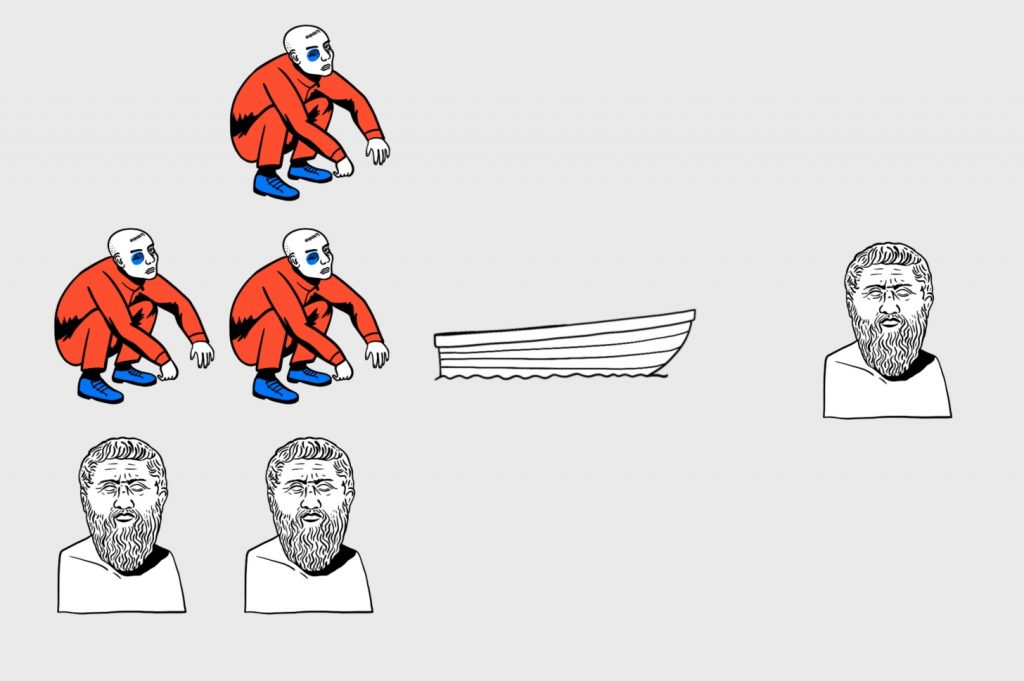
Теперь прикинем варианты следующего рейса. Мы не можем отправить двух гопников, иначе философы останутся в большинстве, и настанет на левом берегу полный экзистенциализм.
Поэтому снова на тот берег уплывают философ с гопником. Причём гопник высаживает философа, но сам из лодки не вылезает — если так не сделать, то он останется с двумя философами на том берегу и они увлекут разговорами об идеях вещей:
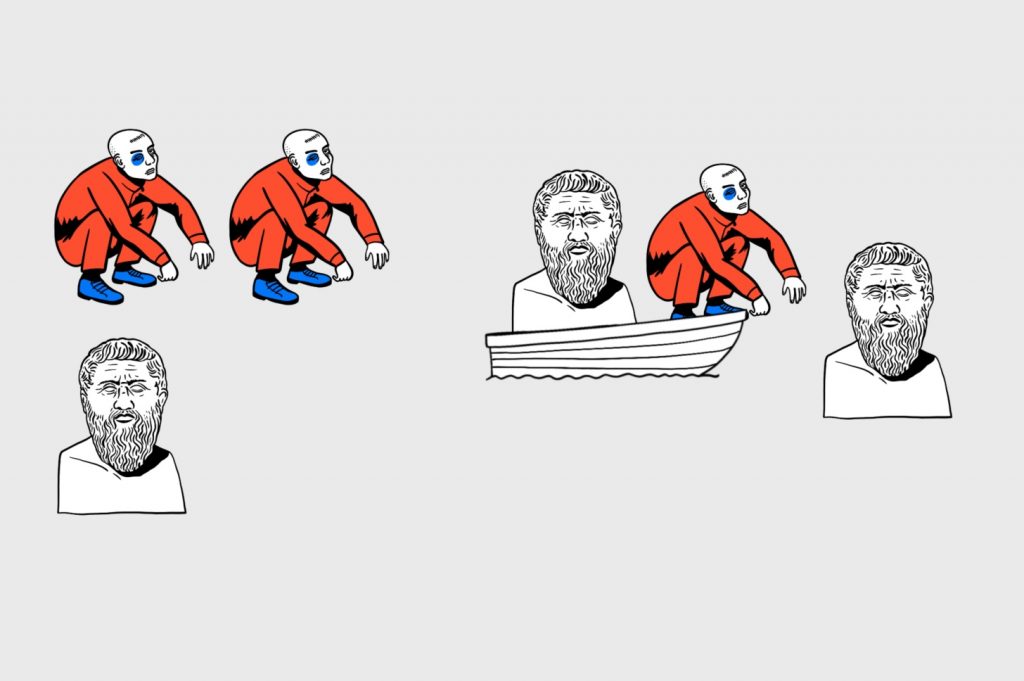
Таким образом, у нас на том берегу сидят два философа, а на этом — один философ и три гопника, на которых он вряд ли сможет воздействовать силой дискурса:
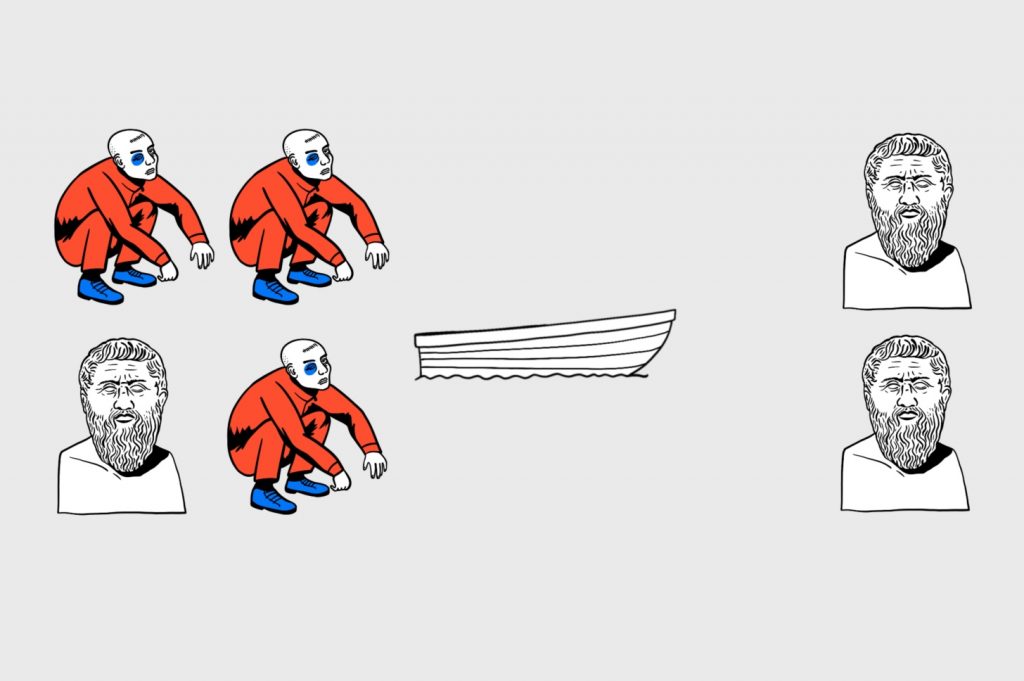
Задача про волка козу и капусту ➄ Как перевезти?
Теперь нам нужно сделать выбор, кто поедет на этот раз. Можно отправить снова философа и гопника, но тогда на том берегу окажутся три философа. И безопасно перевезти остальных гопников поодиночке уже не получится — философы всегда будут в большинстве.
Значит, остаётся только один вариант: отправить в путь двух гопников. В итоге на том берегу всех будет поровну и всё пройдёт спокойно:
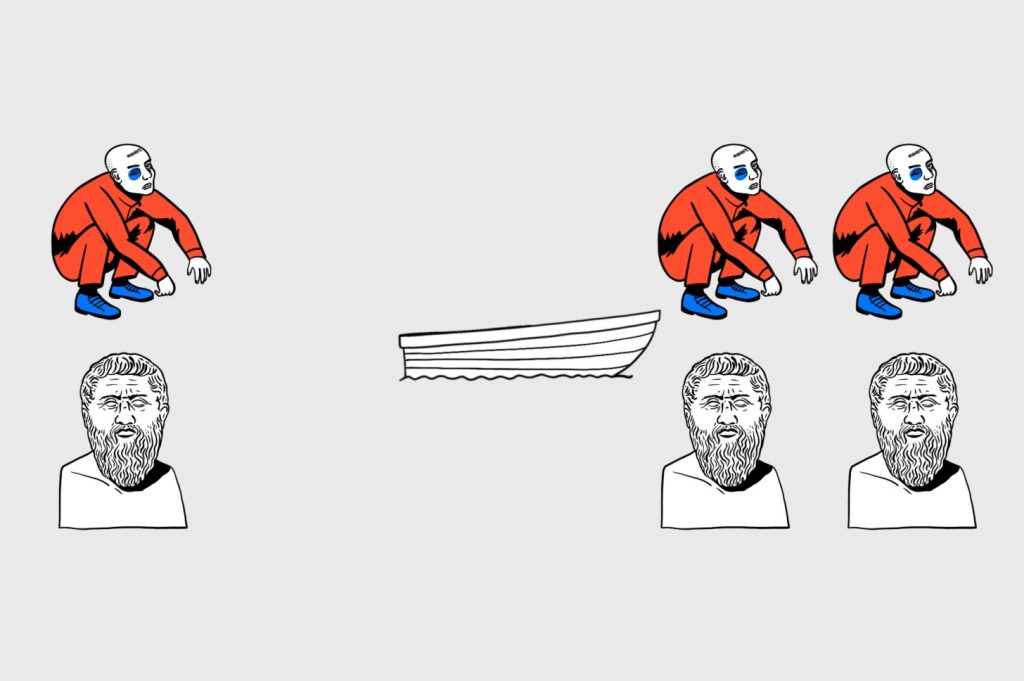
Но лодку надо как-то отправить на другой берег. Нельзя разместить на ней одного гопника, потому что второй останется в меньшинстве среди философов. Двум гопникам ехать обратно тоже не вариант, потому что они только что прибыли.
Поэтому назад отправляются философ и гопник:
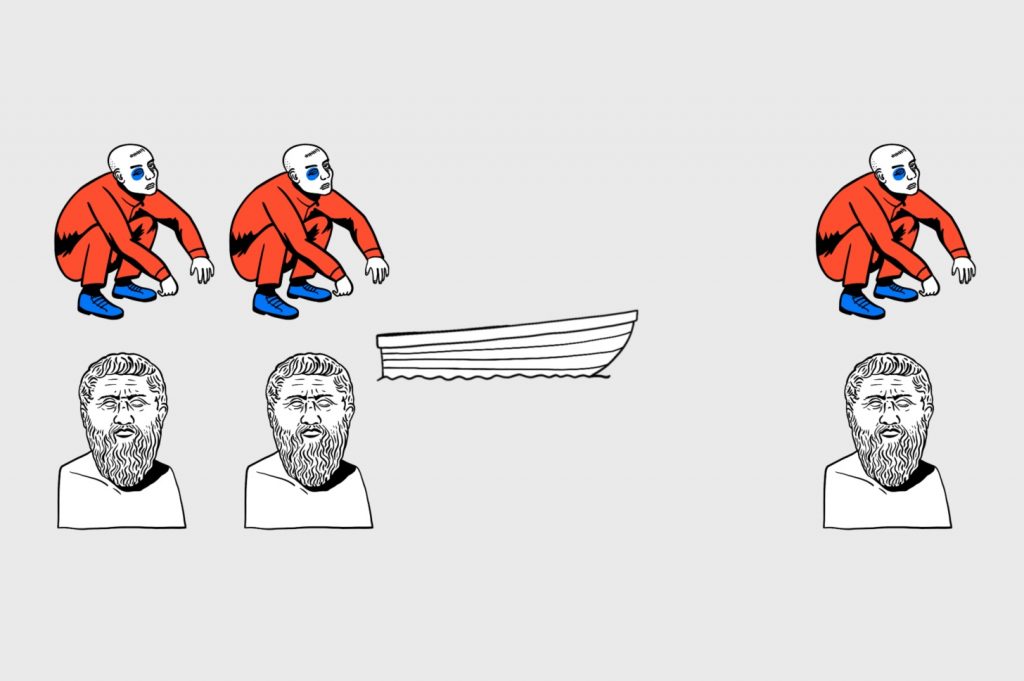
Теперь единственный безопасный вариант — отправить на тот берег двух гопников:
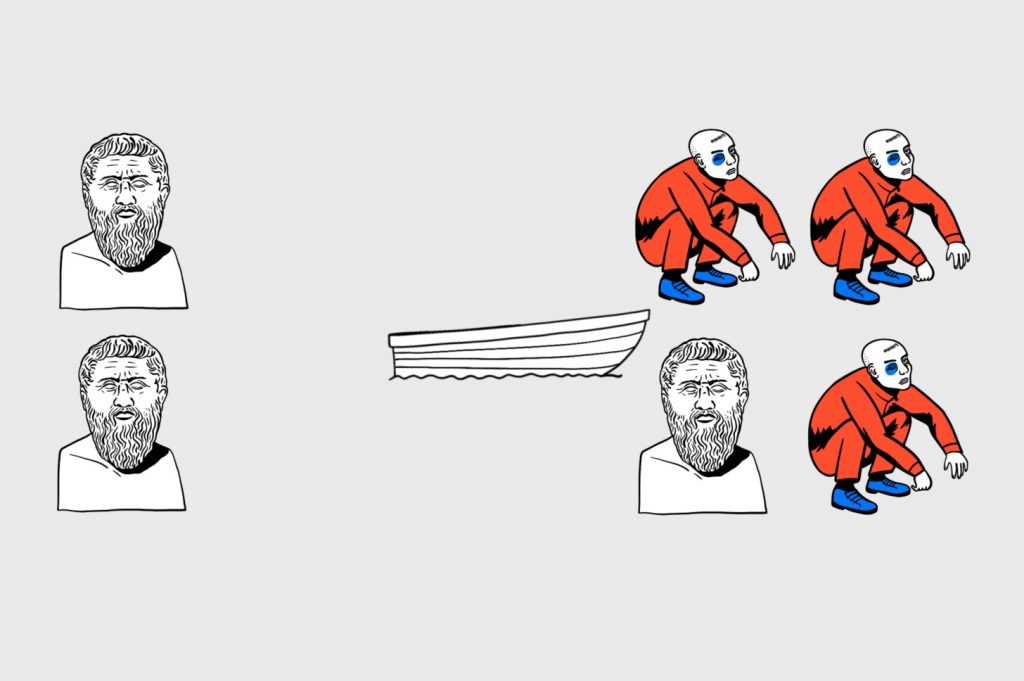
Назад отправим одного гопника. Чтобы не выходить из лодки, он позовёт в неё философа (например, фразой «Что вы думаете о солипсизме?») и вернётся с ним обратно на тот берег:
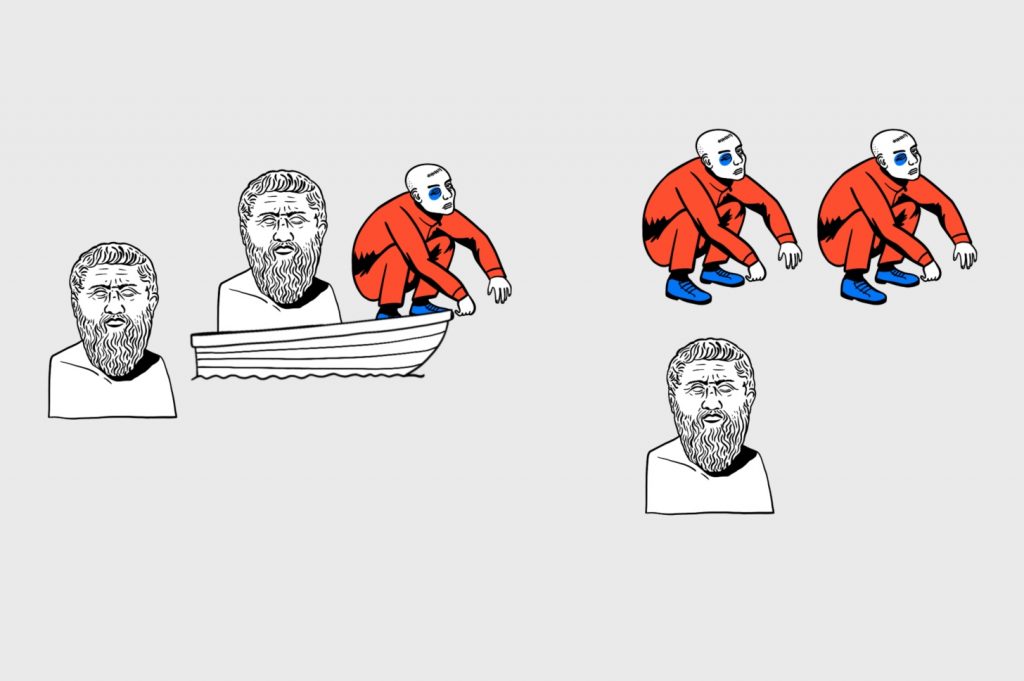
Точно так же забираем оставшегося философа:
И в итоге вся компания оказывается на том берегу, бездонное небо — над головой, а нравственный закон — внутри:
Получите ИТ-профессию
В «Яндекс Практикуме» можно стать разработчиком, тестировщиком, аналитиком и менеджером цифровых продуктов. Первая часть обучения всегда бесплатная, чтобы попробовать и найти то, что вам по душе. Дальше — программы трудоустройства.




Еще по теме

Недетская задача про детей
Безумный диалог двух программистов может свести с ума любого умного человека, но не вас.

Зубодробительная задачка с очень простой математикой
Эта задача поставит в тупик половину интернета, но не вас.

Начинающим программистам: что такое фреймворки и библиотеки

Задачка: как подбросить гнутую монетку
Что делать, если вероятность выпадения не 50 на 50?

Задача про бабушку и домашний изюм
Сложная задача с несложной математикой
Шок-задача про длинный мост

Задача про номер дома
Диалог программистов с зубодробительной логикой

Задачка: узнать среднюю зарплату в строгой компании
Непростая задачка против звериного оскала капитализма.
Источник: thecode.media
Основы алгоритмизации
Решение задач, для закрепления материала.
Задача №1. Старик должен переправить на лодке через реку волка, козу и капусту. Лодка может выдержать только старика и одного “пассажира”. В каком порядке старик перевезет пассажиров? Не забудь, что волк может съесть козу, а коза – капусту.
Найди 2 варианта решения.
Решение:
Решение удобно записать в виде таблицы, указывая текущее положение объектов при переправе: кто на каком берегу остался, кто переправляется.
Исходное состояние
Старик, Волк, Коза, Капуста
1 шаг
Волк, Капуста — левый берег
> Старик, Коза — способ действия
2 шаг
Волк, Капуста — левый берег
< Старик — способ действия
Коза — правый берег
3 шаг
Капуста — левый берег
> Старик, Волк — способ действия
Коза — правый берег
4 шаг
Капуста — левый берег
< Старик, Коза — способ действия
Волк — правый берег
5 шаг
Коза — левый берег
> Старик, Капуста — способ действия
Волк — правый берег
6 шаг
Коза — левый берег
< Старик — способ действия
Волк, Капуста — правый берег
7 шаг
> Старик, Коза — способ действия
Волк, Капуста — правый берег
Результат
Старик, Волк, Коза, Капуста — правый берег
Если возникли трудности при решение, целесообразно ответить на вопросы:
- Может ли перевозчик поплыть на лодке один, оставив на берегу всех троих – волка, козу и капусту?
- Может ли перевозчик поплыть на другой берег с одним из «пассажиров», а вернуться с другим?
Задача №2.Выполните предложенные действия.
- Задумайте целое число от 1 до 20.
- Результат умножьте на 2.
К полученному произведению прибавьте 3.
К разности прибавьте 5.
Сообщите ответ.
Что у вас получилось? Объясните, в роли какого исполнителя – формального или неформального – вы выступали. Попробуйте поменять местами две любые команды. Получится ли у вас тот же результат?
Решение: Очень хочется надеяться, что вы были внимательны, и у вас получилось число 12. Если получилось другое число, то выми допущена ошибка в вычислениях, так как последовательность действий была такова:
Ответ: В данном случае вы выступали в качестве формального исполнителя, т.к. выполняли команды. Если поменять команды местами, то ответ будет уже другим. Если выполнять эти команды друг за другом, без вычислительных ошибок, то для разных чисел результат будет один и тот же.
Задачи более высокого уровня
Задача №3. Задача про исполнителя команд.
Имеется Исполнитель алгоритма, который может передвигаться по числовой оси. Система команд Исполнителя алгоритма:
«Вперед N»
«Назад M»
Переменные N и M могут принимать любые целые положительные значения. Известно, что Исполнитель алгоритма выполнил программу из 50 команд, в которой команд «Назад 2» на 12 больше, чем команд «Вперед 3». Других команд в программе не было.
Какой одной командой можно заменить эту программу, чтобы Исполнитель алгоритма оказался в той же точке, что и после выполнения программы?
Решение: Найдем сколько было команд «Вперед», а сколько было «Назад». Учитывая, что общее количество команд равно 50 и что команд «Назад» на 12 больше, чем команд «Вперед». Получим уравнение х+(х+12)=50, где х- количество команд «Вперед». Тогда общее количество команд»Вперед» — х=19, а количество команд «Назад»: 19+12=31.
Будем вести отсчет от начала числовой оси. Выполнив 19 раз команду «Вперед3», Исполнитель алгоритма оказался на отметке числовой оси 57 (19*3=57). После выполнения 31 раз команды «Назад2» (31*2=62) он оказался бы на отметке -5. (57-62=-5).
Все эти команды можно заменить на одну команду «Назад 5»
Задача №4. Числа Фибоначчи.
Леонардо Пизанский, известный, как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Числовой ряд, который назван его именем, получился в результате решения задачи о кроликах, которую Фибоначчи изложил в своей «Книге Абака»(1202 год).
Он выглядит так: 1,1,2,3,5,8,13,21,34,55,89,144…
В этом ряду каждое следующее число, начиная с третьего, равно сумме двух предыдущих.
Составьте словесный алгоритм проверки принадлежности введенного числа n ряду Фибоначчи.
Решение:
1. Ввести число N.
2. Установить значение первых трех чисел Фибоначчи: 1,1,2.
3. Пока введенное число N больше очередного числа Фибоначчи, взять два последних числа Фибоначчи и получить из них новое число Фибоначчи.
3. Если число Фибоначчи равно введенному N или было введено число N=1, значит, что было введено число Фибоначчи, в противном случае – введенное число не является числом Фибоначчи.
Приведенный словесный алгоритм сожержит начальные установки, в пункте 3 цикл с условием, а пункт 4 – это вывод результата работы алгоритма.
Источник: osnovialgoritmizaziimodule.blogspot.com
Перевезти через реку волка, козу и капусту — Prolog
Здравствуйте. Требуется задача на Turbo Prolog: Крестьянину нужно перевезти через реку волка, козу и капусту. На реке есть лодка, на которой может поместиться только крестьянин и волк, или крестьянин и коза, или крестьянин и капуста. В то время пока крестьянин перевозит в лодке один из своих товаров, остальные два ждут его на берегах.
Волка и козу нельзя оставлять на одном берегу без присмотра человека, потому что волк съест козу. Так же нельзя оставлять козу наедине с капустой. Указать последовательность действий, которая позволит крестьянину переправить всех троих невредимыми. Заранее спасибо !
Код к задаче: «Перевезти через реку волка, козу и капусту»
Листинг программы
domains slist=string* state=wgc(string, slist, slist) history=state* moves=string* predicates solve_dfs(state, history, moves) initial_state(state) final_state(state) move(state, string) member(string, slist) member1(state, history) update(state, string, state) update_boat(string, string) update_bank(string, string, slist, slist, slist,slist) select(string, slist, slist) insert(string, slist, slist) precedes(string, string) legal(state) illegal(slist) test clauses test:-initial_state(State), solve_dfs(State, [State], Moves), write(Moves). solve_dfs(State, _, [])if final_state(State). solve_dfs(State, History, [Move|Moves]):- move(State, Move), update(State, Move, State1), legal(State1), not (member1(State1, History)), solve_dfs(State1, [State1|History], Moves). initial_state(wgc(left, [wolf, goat, cabbage], [])). final_state(wgc(right, [], [wolf, goat, cabbage])). move(wgc(left, L, _), Cargo)if member(Cargo, L). move(wgc(right, _, R), Cargo)if member(Cargo, R). move(wgc(_, _, _), alone). update(wgc(B, L, R), Cargo, wgc(B1, L1, R1)) :- update_boat(B, B1), update_bank(Cargo, B, L, R, L1, R1). update_boat(left, right). update_boat(right, left). update_bank(alone, _, L, R, L, R). update_bank(Cargo, left, L, R, L1, R1):- select(Cargo, L, L1), insert(Cargo, R, R1). update_bank(Cargo, right, L, R, L1, R1):- select(Cargo, R, R1), insert(Cargo, L, L1). insert(X, [Y|Ys], [X,Y|Ys]):- precedes(X, Y). insert(X, [Y|Ys], [Y|Zs]):- precedes(Y, X), insert(X, Ys, Zs). insert(X, [], [X]). precedes(wolf, _). precedes(_, cabbage). legal(wgc(left, _, R)):- not(illegal(R)). legal(wgc(right, L, _)):- not(illegal(L)). illegal(L):- member(wolf, L), member(goat, L). illegal(L):- member(goat, L), member(cabbage, L). select(X, [X|Xs], Xs). select(X, [Y|Ys], [Y|Zs]):- select(X, Ys, Zs). member(X, [X|_]). member(X, [_|Ys]):- member(X, Ys). member1(X, [X|_]). member1(X, [_|Ys]):- member1(X, Ys). goal test.
Источник: studassistent.ru