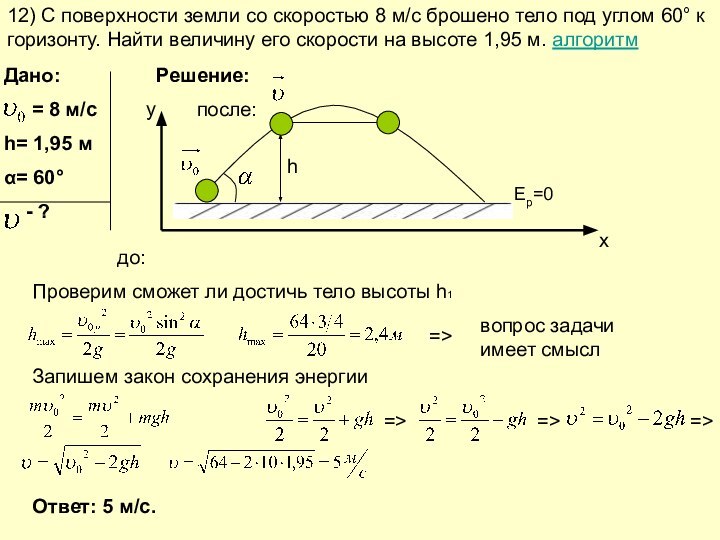
64. Снаряд массой m = 5 кг, вылетевший из орудия, верхней точке траектории имеет скорость v = 300 м/с. В этой точке он разорвался на два осколка, причем больший осколок массой m1 полетел в обратном направлении со скоростью v1 = 100 м/с. Определить скорость v2 второго меньшего осколка.
65. Лодка массой M = 150 кг и длиной l = 2,8 м стоит неподвижно в стоячей воде. Рыбак массой m = 90 кг в лодке переходит с носа на корму. Пренебрегая сопротивлением воды, определите, на какое расстояние s при этом сдвинется лодка.
66. Снаряд, вылетевший из орудия со скоростью v0 , разрывается на два одинаковых осколка в верхней точке траектории на расстоянии l (по горизонтали). Один из осколков полетел в обратном направлении со скоростью движения снаряда до разрыва. Пренебрегая сопротивлением воздуха, определите, на каком расстоянии (по горизонтали) от орудия упадет второй осколок.
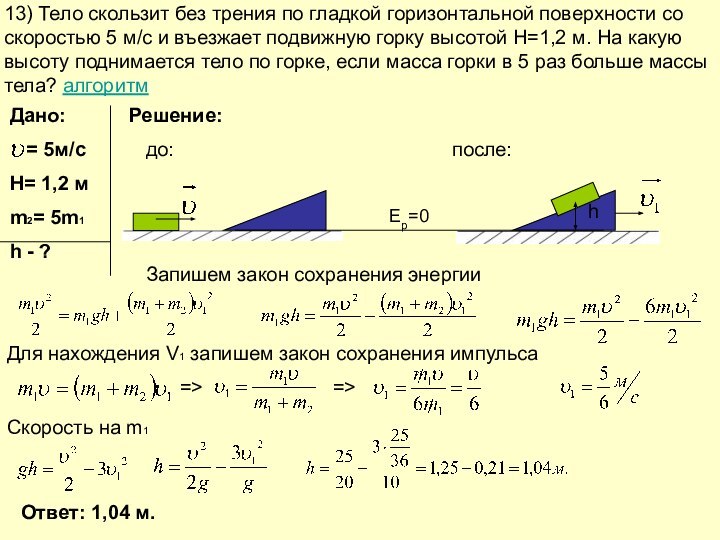
67. Платформа с песком общей массой M = 2 т стоит на рельсах на горизонтальном участке пути. В песок попадает снаряд массой m = 8 кг и застревает в нем. Пренебрегая трением, определите, с какой скоростью будет двигаться платформа, если в момент попадания скорость снаряда v = 450 м/с, а ее направление — сверху вниз под углом α = 30° к горизонту.
CHASER 800 ADMIRAL
68. На железнодорожной платформе, движущейся по инерции со скоростью v0 = 3 км/ч, укреплено орудие. Масса платформы с орудием M = 10 т. Ствол орудия направлен в сторону движения платформы. Снаряд массой m = 10 кг вылетает из ствола под углом α = 60° к горизонту. Определить скорость v снаряда (относительно Земли), если после вылета скорость платформы уменьшилась в n = 2 раза.
69. Две легкие тележки (массы соответственно m1 и m2 = 2m1) соединены между собой сжатой, связанной нитью пружиной. Пережигая нить, пружина распрямляется, и тележка разъезжается в разные стороны. Считая коэффициент трения для обеих тележек одинаковый, определить: 1) v1/v2 – отношение скоростей движения тележек; 2) t1/t2 – отношение времени, в течении которого тележки движутся; 3) s1/s2 – отношение путей пройденных тележкой.
70. Две одинаковые тележки массой М каждая движутся по инерции (без трения) друг за другом с одинаковой скоростью v0. В какой-то момент времени человек массой m, находящийся на задней тележке, прыгнул на переднюю тележку со скоростью u относительно своей тележки. Определите скорость v1 передней тележки.
71. Определите положение центра масс системы, состоящей из четырех шаров, массы которых равны соответственно m, 2m, Зm и 4m, в следующих случаях: а) шары расположены на одной прямой; б) шары расположены по вершинам квадрата; в) шары расположены по четырем смежным вершинам куба. Во всех случаях расстояние между соседними шарами равно 15 см. Направление координатных осей показано на рисунке.
72. Определите положение центра масс половины круглого диска радиусом R, считая его однородным.
73. Определите координаты центра масс системы, состоящей из четырех шаров массами 2m, Зm, 4m и т, которые расположены в вершинах и в центре равностороннего треугольника со стороной a = 20 см. Направление координатных осей показано на рисунке.
САЛЮТ 480 NEO. Тюнинг проект. Лодка Антона Fisherman-a.
74. нагруженная песком железнодорожная платформа с начальной массой m0 начинает движение из состояния покоя под действием постоянной силы тяги F. Через отверстие в дне платформы высыпается песок с постоянной скоростью μ (кг/с) Определить v(t), т.е. зависимость скорости платформы от времени.
75. На катере массой m = 4,5 т находится водомет, выбрасывающий со скоростью u = 6 м/с относительно катера назад μ = 25 кг/с воды. Пренебрегая сопротивлением движению катера, определите: 1) скорость катера через t = 3 мин после начала движения; 2) предельно возможную скорость катера.
76. Ракета, масса которой в начальный момент времени М = 2 кг, запущена вертикально вверх. Относительная скорость выхода продуктов сгорания u = 150 м/с, расход горючего μ = 0,2 кг/с. Пренебрегая сопротивлением воздуха, определить ускорение a ракеты через t = 3 с после начала её движения. Поле силы тяжести считать однородным.
77. Ракета, масса М которой в начальный момент времени равна 300 г, начинает выбрасывать продукты сгорания с относительной скоростью u = 200 м/с. Расход горючего μ = 100 г/с. Пренебрегая сопротивлением воздуха и внешним силовым полем, определить: 1) за какой промежуток времени скорость ракеты станет равной v1 = 50 м/с; 2) скорость v2, которой достигнет ракета, если масса заряда m0 = 0,2 кг.
78. Ракета с начальной массой m0, начиная движение из состояния покоя, к некоторому моменту времени t израсходовав топливо массой m, развивает скорость v. Пренебрегая сопротивлением воздуха и внешним силовым полем, определите зависимость v от m, если скорость истечения топлива относительно ракеты равна u.
79. Ракета поднимается с нулевой начальной скоростью вертикально вверх. Начальная масса ракеты m0, скорость истечения газа относительно ракеты постоянна и равна u. Пренебрегая сопротивлением воздуха, выразите скорость ракеты v в зависимости от m и t (m — масса ракеты; t — время ее подъема). Поле силы тяжести считайте однородным.
80. Ракета с начальной массой m0 = 1,5 кг, начинает движение из состояния покоя вертикально вверх, выбрасывая непрерывную струю газов с постоянной скоростью относительно нее скорости u = 600 м/с. Расход газа μ = 0,3 кг/c. Определить, какую скорость приобретет ракета через 1 секунду после начала движения, если она движется: 1) при отсутствии внешних сил; 2) в однородном поле силы тяжести. Оценить относительную погрешность, сделанную для данных условий задачи при пренебрежении внешним силовым полем.
Источник: studyport.ru
Лодка длиной L = 3 м и массой m = 120 кг стоит на спокойной воде. На носу и корме находятся два рыбака массами m1 = 60 кг и m2 = 90 кг. На сколько сдвинется лодка относительно воды, если рыбаки пройдут по лодке и поменяются местами? (Решение → 21710)
Лодка длиной L = 3 м и массой m = 120 кг стоит на спокойной воде. На носу и корме находятся два рыбака массами m1 = 60 кг и m2 = 90 кг. На сколько сдвинется лодка относительно воды, если рыбаки пройдут по лодке и поменяются местами?
(полное условие в демо-файлах)







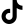


Библиотека Ирины Эланс, основана как общедоступная библиотека в интернете. Онлайн-библиотеке академических ресурсов от Ирины Эланс доверяют студенты со всей России.
Библиотека Ирины Эланс
Полное или частичное копирование материалов разрешается только с указанием активной ссылки на сайт:
Ирина Эланс открыла библиотеку в 2007 году.
Источник: student-files.ru
Презентация на тему Алгоритм решения задач по теме Законы сохранения
до m1m2Закон сохранения импульсаm1V1+m2V2=(m1+m2)V XВ проекции на ось Х:m1V1+m2V2=(m1+m2)V V=m1V1+m2V2m1+m2m1V1-m2V2=(m1+m2)V V=m1V1-m2V2m1+m2m1m2V1V2VV1V2V1) Мальчик догоняет тележку (бежит навстречу тележке) и запрыгивает на нее. Дальше они двигаются вместе. Масса мальчика m1, масса тележки m2. Скорость мальчика V1
- Главная
- Математика
- Алгоритм решения задач по теме Законы сохранения


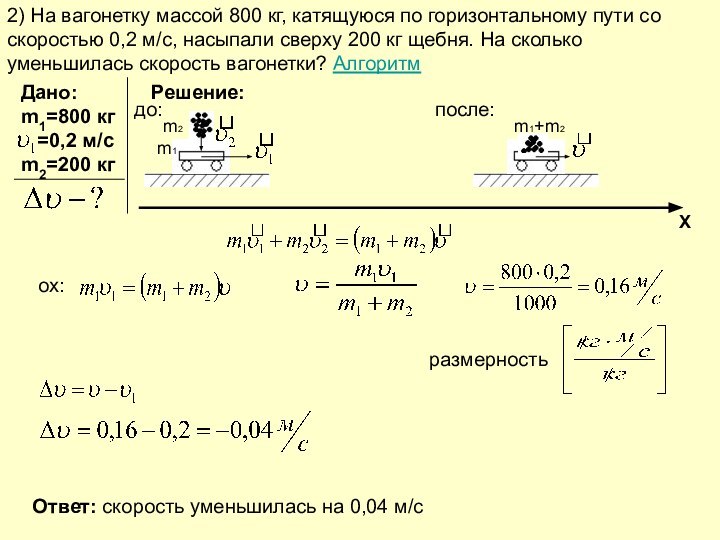

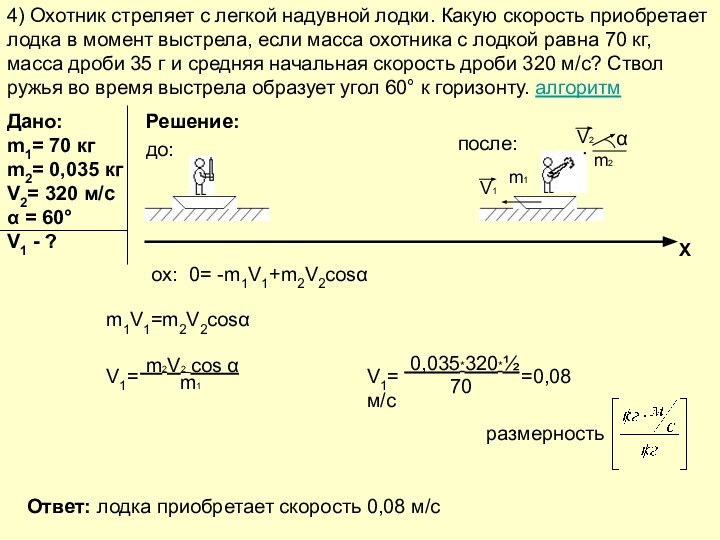
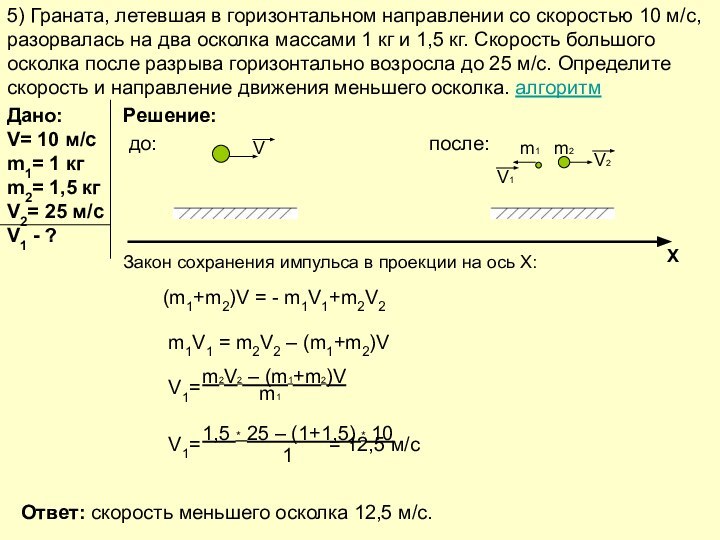





















Слайды презентации
Слайд 1 11, 21, 2, 31, 2, 3, 41, 2,

3, 4, 51, 2, 3, 4, 5, 61, 2,
3, 4, 5, 6, 71, 2, 3, 4, 5, 6, 7, 81, 2, 3, 4, 5, 6, 7, 8, 91, 2, 3, 4, 5, 6, 7, 8, 9, 101, 2, 3, 4, 5, 6, 7, 8, 9, 10, 111, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 121, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 131, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 141, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 151, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 161, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 171, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 181, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 191, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 201, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 211, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 221, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 231, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24
Алгоритм решения задач по теме «Законы сохранения»
1) Внимательно изучите условие задачи, поймите физическую сущность явлений и процессов, рассматриваемых в задаче, уясните основной вопрос задачи.
2) Мысленно представьте ситуацию, описанную в задаче, выясните цель решения, четко выделите данные и неизвестные величины.
3) Запишите краткое условие задачи. Одновременно выразите все величины в единицах СИ.
4) Сделайте чертеж, на котором отобразите ситуацию до и после события.
5) Запишите закон сохранения импульса (в проекции на выбранную ось) проверив систему на замкнутость или (и) закон сохранения энергии в соответствии с тем, что отобразили на чертеже (с одной стороны равенства что было «до», с другой что «после»). Выберите нулевой уровень потенциальной энергии.
6) Решите уравнение или систему уравнений относительно неизвестной величины, т.е. решите задачу в общем виде.
7) Если не все величины известны, то для нахождения их можете применить алгоритм решения задач по теме «Динамика».
8) Найдите искомую величину.
9) Определите единицу величины. Проверьте, подходит ли она по смыслу.
10) Рассчитайте число.
11) Проверьте ответ на «глупость» и запишите его.
Слайд 2 до
m1
m2
Закон сохранения импульса
m1V1+m2V2=(m1+m2)V
X
В проекции

на ось Х:
m1V1+m2V2=(m1+m2)V
навстречу тележке) и запрыгивает на нее. Дальше они двигаются вместе. Масса мальчика m1, масса тележки m2. Скорость мальчика V1 , скорость тележки V2 . Алгоритм
Слайд 3 2) На вагонетку массой 800 кг, катящуюся по

горизонтальному пути со скоростью 0,2 м/с, насыпали сверху
200 кг щебня. На сколько уменьшилась скорость вагонетки? Алгоритм
Дано:
m1=800 кг
=0,2 м/с
m2=200 кг
Ответ: скорость уменьшилась на 0,04 м/с
Слайд 4 3) Рыбак массой 60 кг переходит с носа

на корму лодки. На сколько переместится лодка длиной 3
м и массой 120 кг относительно воды? алгоритм
считаем движение рыбака и лодки равномерным
подставляем в уравнение
Источник: findtheslide.com