Решение уравнений на скорость лодки

После того как вы поделитесь материалом внизу появится ссылка для скачивания.

Получить код —>

Подписи к слайдам:

Решение задач с помощью дробных рациональных уравнений

МБОУ «Гимназия № 94»

Московского района г.Казани

• Организационный момент. Повторение.

2. Актуализация знаний. Объяснение нового материала.

2.1 Задачи на движение. Задача № 1.

2.2. Алгоритм решения задач.

2.3.Задачи на движение по воде.

3. Закрепление новой темы. Задача № 2.

4. Самостоятельная работа.

6. Домашнее задание. Рефлексия.

1. Какие из представленных ниже уравнений дробные рациональные?

2. Какое уравнение называется дробным рациональным?

Левая или правая части уравнения являются рациональными дробными выражениями.

(работа в парах по вариантам)

Алгоритм решения дробного рационального уравнения.

• Все переносим в левую часть.
• Приводим дроби к общему знаменателю.
• Заменяем уравнение на систему:

Дробь равна нулю, тогда и только тогда, когда числитель равен нулю, а знаменатель нулю не равен.

Как решают уравнения в России и США!?

Из пунк­тов А и В, рас­сто­я­ние между ко­то­ры­ми 27 км, вышли од­но­вре­мен­но нав­стре­чу друг другу два пе­ше­хо­да и встре­ти­лись в 15 км от А. Най­ди­те ско­рость пе­ше­хо­да, шед­ше­го из А, если из­вест­но, что он шёл со ско­ро­стью, на 2 км/ч боль­шей, чем вто­рой пе­ше­ход, и сде­лал в пути по­лу­ча­со­вую оста­нов­ку.

2.1. Задачи на движение

2.1. Задачи на движение

Пусть скорость пе­ше­хо­да, шед­ше­го из А равна х км/ч, тогда скорость пешехода шедшего из В равна (х-2) км/ч.

Пешеход из А прошел 15 км, а расстояние между пунктами 27 км, следовательно пешеход их В прошел 12 км. 27-15=12.

2.1. Задача на движение

Решение задачи № 1

По условию пешеход из А сде­лал в пути по­лу­ча­со­вую оста­нов­ку, значит он шел меньше времени на 0,5 ч . Это условие можно записать так t1< t2 на 0,5 ч. или t2 — t1 = 0,5.

Корень х = -10 не удовлетворяет условию задачи. Получаем, что скорость пешехода из А равна 6 км/ч.

Ответ : скорость пешехода из А равна 6 км/ч.

2. Задача на движение

Решение задачи № 1

2.2. Алгоритм решения задач

V -скорость ( км/ч ; м/сек)

t — время ( ч; мин; сек)

S — пройденный путь (км; м)

• Определяем какую величину берем за переменную.
• По условию задачи заполняем таблицу.
• Составляем уравнение и его решаем.
• Анализируем получившиеся корни уравнения (убираем те, которые не удовлетворяют условию задачи).
• Делаем дополнительные вычисления или пишем сразу ответ (зависит от того, что нужно найти в задаче).

Основная формула используемая в задачах,

• Определяем какую величину берем за переменную.
• По условию задачи заполняем таблицу.
• Составляем уравнение и его решаем.
• Анализируем получившиеся корни уравнения (убираем те, которые не удовлетворяют условию задачи).
• Делаем дополнительные вычисления или пишем сразу ответ (зависит от того, что нужно найти в задаче).

Очень часто основу уравнения составляет условие, которое накладывается на время.

Решение задач с помощью уравнений.

Для удобства условие можно записать в виде неравенства.

2.3. Задачи на движение по воде

В задачах при движении по воде используются четыре вида скорости. Какие?

V лодки = V по озеру

• Собственная скорость (лодки, катера, теплохода…).
• Скорость течения реки.
• Скорость по течению реки.
• Скорость против течения реки.

2.3. Задачи на движение по воде

В задачах при движении по воде используются четыре вида скорости. Какие ?

V плота = V течения реки

V лодки = х (ед. из)

Vтечения = у(ед. из)

Источник: uchitelya.com

Как решать задачи на скорость по течению и против течения реки 6 класс кратко

При решении задач на движение, главное найти три ключевые величины: расстояние, время и скорость. Для этих величин можно записать один из законов движения:

Сегодня в этой статье мы познакомимся с задачами на движение по течению и против течения реки. Также рассмотрим задачи на сближение и удаление. Также стоит помнить, что в таких задачах данные величины нужно приводить к единой системе единиц.

Задача 1. Катер плыл против течения реки (120) км, назад он плыл, затратив на путь на (2) часа меньше. Найдите скорость катера без течения реки, если скорость течения (1) км/час.

Задача 2. Человек плывет со скоростью (5) км/ч. Если скорость течения равна (1) км/ч, то ему требуется (1) час, чтобы плыть к месту и вернуться обратно. Найдите расстояние до этого места.

Решение. Пусть расстояние х км и скорость по течению будет равна (5+1=6) км/ч. Скорость против течения тогда (5-1=4) км /ч. Составим уравнение (frac+frac=1) , так как (s/v=t) .

Задача 3. За один час лодка проходит (11) км по течению и (5) км против течения. Найтите скорость лодки в стоячей воде.

Задача 4. Если Максим плывет (15) км против течения за (3) часа и за это же время — (21) км по течению. Найтите скорость течения.

Задача 5. За один час лодка проходит (11) км по течению и (5) км против него. Найтите скорость лодки в неподвижной воде.

Задача 6. Вика плывет со скоростью (4) км/ч. Если скорость течения равна (1) км/ч и ей требуется (1) час, чтобы плыть к месту и вернуться обратно. Найдите расстояние до этого места.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Репетитор 5-11 классов. Для меня математика — язык общения с миром. Всегда важно понимать, что стоит за той или иной цифрой, формулой, уравнением, понимать, какой смысл в себе они несут. Этому языку я обучаю своих учеников, помогаю полюбить его и научить умело применять в жизни. В преподавании основываюсь на том, чтобы закладывать основательные знания.

Если фундамент прочный, то дальнейшее обучение всегда просто. Если есть трудности, то помогу найти и восполнить пробел. В каждом ученике я вижу личность и учитываю его индивидуальные особенности. В обучении использую идеи Льва Толстого. Преподаю с Любовью.

Жду вас на своих уроках.

Репетитор 1-9 классов по русскому языку. Доброжелательное отношение, создание позитивной эмоциональной атмосферы на занятиях, эффективная отработка материала обеспечивают самые высокие результаты. Стараюсь привить любовь к предмету у ребенка, использую индивидуальный подход, подбираю материал в зависимости от способностей ребёнка. Приветствую в учениках ответственное отношение, дисциплинированность и стремление учиться.

Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.

Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.

Задача 1. Катер движется против течения реки. За сколько часов он преодолеет расстояние 112 км, если его собственная скорость 30 км/ч, а скорость течения реки 2 км/ч?

Решение: Сначала узнаем скорость движения катера против течения реки, для этого от его собственной скорости отнимем скорость течения:

30 — 2 = 28 (км/ч) — скорость движения катера против течения.

Теперь можно узнать за сколько часов катер преодолеет 112 км, разделив расстояние на скорость:

Решение задачи по действиям можно записать так:

1) 30 — 2 = 28 (км/ч) — скорость движения катера против течения,

Ответ: За 4 часа катер преодолеет расстояние 112 км.

Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки.

Задача 2. Расстояние от пункта A до пункта B по реке равно 120 км. Сколько времени потратит моторная лодка на путь от пункта A до B, если её собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?

Рассмотрите два варианта:

1) лодка движется по течению реки;

2) лодка движется против течения реки.

Решение: Если моторная лодка будет двигаться по течению реки, то её скорость будет равна сумме собственной скорости со скоростью течения реки:

Значит расстояние между пунктами лодка преодолеет за:

Если лодка будет двигаться против течения реки, то её скорость будет равна разности собственной скорости и скорости течения реки:

Значит, чтобы узнать сколько времени потратит лодка на путь от пункта A до пункта B, надо расстояние разделить на скорость:

Решение задачи по действиям для движения по течению реки можно записать так:

1) 27 + 3 = 30 (км/ч) — скорость лодки,

Для движения против течения реки решение задачи по действиям можно записать так:

1) 27 — 3 = 24 (км/ч) — скорость лодки,

1) При движении по течению реки моторная лодка потратит 4 часа на путь от пункта A до пункта B.

2) При движении против течения реки моторная лодка потратит 5 часов на путь от пункта A до пункта B.

Задача 1

Скорость катера в стоячей воде равна 15 км/ч, а скорость течения реки — 3 км/ч. Какова скорость катера по течению и против течения реки?

1) 15 + 3 = 18 (км/ч) — скорость катера по течению реки,

2) 15 — 3 = 12 (км/ч) — скорость катера против течения реки.

Ответ. 18 км/ч и 12 км/ч.

Задача 2

Скорость моторной лодки по течению реки равна 48 км/ч, а против течения — 42 км/ч. Какова скорость течения реки и собственная скорость моторной лодки?

1) 48 — 42 = 6 (км/ч) — удвоенная скорость течения реки,

2) 6: 2 = 3 (км/ч) — скорость течения реки,

3) 48 — 3 = 45 (км/ч) — собственная скорость.

Ответ. 3 км/ч и 45 км/ч.

Задача 3

Скорость моторной лодки в стоячей воде 12 км/ч. По течению она плыла 2,6 ч, против течения 3,15 ч. Найдите скорость течения реки, если путь по течению на 10,8 км больше чем против течения.

Пусть скорость течения х км/ч

2,6(12 + х) — расстояние, которое проплыла лодка по течению;

3,15(12 — х) — расстояние, которое проплыла лодка против течения.

2,6(12 + х) — 3,15(12 — х) = 10,8 км/ч

Задача 4

Сергей знает, что собственная скорость его лодки равна 10 км/ч. При этом ему надо успеть проплыть 25 км за 2 часа. Плыть он будет по течению. Какой должна быть скорость течения реки, чтобы Антон успел?

Чтобы Антон успел, необходимо и достаточно, чтобы его лодка перемещалась со скоростью не меньше, чем 25 : 2 = 12,5 км/ч. То есть для того, чтобы Антон успел, необходимо и достаточно, чтобы скорость течения была не меньше, чем 2,5 км/ч.

Задача 5

Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч.

Задача 6

На озере расположены пристани А и В. Расстояние между пристанями равно 90 км. Моторная лодка проплыла от А до В с постоянной скоростью, после чего сразу отправилась обратно со скоростью на 5 км/ч больше прежней. На середине пути из В в А лодка замедлилась и поплыла со скоростью на 2,5 км/ч меньшей, чем по дороге из А в В. В результате лодка затратила на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость лодки на пути из А в В.

Задача 7

Пароход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость парохода в неподвижной воде равна 15 км/ч, стоянка длится 10 часов, а в пункт отправления пароход возвращается через 40 часов после отплытия из него.

Задача 8

От пристани A к пристани B, расстояние между которыми равно 420 км, отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним, со скоростью на 1 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно.

Задача 9

Баржа в 10:00 вышла из пункта в пункт , расположенный в 15 км от Пробыв в пункте 1 час 20 минут, баржа отправилась назад и вернулась в пункт в 16:00 того же дня. Определите (в км/час) скорость течения реки, если известно, что собственная скорость баржи равна км/ч.

Задача 10

Расстояние между пристанями и равно 120 км. Из в по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт , тотчас повернула обратно и возвратилась в К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч.

Задача 11

Весной катер идёт против течения реки в раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

Задачи на движение по реке трудны для пятиклассников, а взрослые недоумевают: чего же там трудного? Бревно или плот плывут со скоростью течения реки V т., которая считается постоянной.

Скорость катера в стоячей воде V с. называют собственной скоростью катера. Скорость катера по течению реки V по теч. больше собственной скорости катера на скорость течения реки: V по теч. = V с. + V т.

Скорость катера против течения реки V пр теч. меньше собственной скорости катера на скорость течения реки: V пр. теч. = V с. – V т.

Эти соотношения полезно проиллюстрировать рисунком.

Скорость катера по течению больше его скорости против течения на две скорости течения.

Задача 1. Скорость катера в стоячей воде равна 15 км/ч, а скорость течения реки – 3 км/ч. Какова скорость катера по течению и против течения реки?

Решение.
1) 15 + 3 = 18 (км/ч) — скорость катера по течению реки,
2) 15 – 3 = 12 (км/ч) — скорость катера против течения реки.

Ответ. 18 км/ч и 12 км/ч.

Обратим внимание: скорость катера по течению реки — это сумма его собственной скорости и скорости течения реки, а скорость катера против течения реки— это разность его собственной скорости и скорости течения реки, поэтому скорость по течению реки больше скорости против течения на удвоенную скорость течения .

Задача 2. Скорость моторной лодки по течению реки равна 48 км/ч, а против течения — 42 км/ч. Какова скорость течения реки и собственная скорость моторной лодки?

Решение.
1) 48 – 42 = 6 (км/ч) — удвоенная скорость течения реки,
2) 6 : 2 = 3 (км/ч) — скорость течения реки,
3) 48 – 3 = 45 (км/ч) — собственная скорость.

Ответ. 3 км/ч и 45 км/ч.

Задание 11. ЕГЭ. Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления

Задание. Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч. Ответ дайте в км/ч.

Решение:

Пусть x км/ч – скорость течения реки,

тогда скорость моторной лодки против течения реки равна (11 – x) км/ч,

а скорость моторной лодки по течению реки равна (11 + x) км/ч.

На путь против течения реки моторная лодка затратила 112/(11 – x) ч.,

а на путь по течению реки моторная лодка затратила 112/(11 + x) ч.

Так как на обратный путь (по течению реки) моторная лодка затратила на 6 часа меньше, получим уравнение:

Упростим уравнение, для этого умножим обе части уравнения на (11 – x)·(11 + x), получим

112·(11 + x) – 112·(11 – x) = 6·(11 – x)·(11 + x)

1232 + 112x – 1232 + 112x – 726 + 6x 2 = 0

6x 2 + 224x – 726 = 0

3x 2 + 112x – 363 = 0

D = 112 2 – 4·3·(-363) = 16900

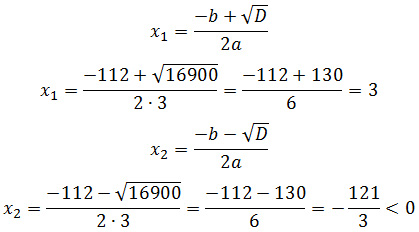
Так как скорость течения реки не может быть отрицательной величиной,

получим ее скорость 3 км/ч.

Ответ: 3

Источник: bezikev.ru