От пристани против течения реки отправилась моторная лодка собственная скорость которой

(- 0,2 посторонний корень)

ответ: скорость лодки в неподвижной воде 20 км/ч

№ 145- Алгебра 8 класс Макарычев

genagnatyk123 22.10.2020 05:39

Искомая скорость x км/ч
1) на 22 км плот затратил 22/2 = 11 ч
значит. лодка была в пути
11-1 = 10 часов, пройдя за это время 99*2 = 198 км
Вниз она плыла со скоростью (x+2) км/ч, а вверх — со скоростью (x-2) км/ч
Составим уравнение
99/(x+2) + 99/(x-2) = 10 и решим его
99(x+2)+99(x-2) = 10(x+2)*(x-2)
99x +198 + 99x- 198 = 10*(x^2-4)
198x = 10*x^2 — 40
10*x^2 -198x -40 =0
D= 198^2 + 4*10*40 = 39204+1600 = 40804
корень(D) = 202
x1= (198+202)/(2*10) = 400/20 = 20 км/ч
x2= (198 -202)/20 = -4/20 = -0,2 — не имеет смысла
ответ: 20 км.ч скорость лодки в неподвижной воде

Источник: otvetgood.ru

ОГЭ 2024, Математика, 9 класс, Демонстрационный вариант, Проект

ОГЭ 2024, Математика, 9 класс, Демонстрационный вариант, Проект.

Демонстрационный вариант контрольных измерительных материалов основного государственного экзамена 2024 года по МАТЕМАТИКЕ.
Экзаменационная работа состоит из двух частей, включающих в себя 25 заданий. Часть 1 содержит 19 заданий, часть 2 содержит 6 заданий с развёрнутым ответом.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 7 и 13 запишите в бланк ответов № 1 в виде одной цифры, которая соответствует номеру правильного ответа.

Примеры.
Вика решила начать делать зарядку каждое утро. В первый день она сделала 30 приседаний, а в каждый следующий день она делала на одно и то же количество приседаний больше, чем в предыдущий день. За 15 дней она сделала всего 975 приседаний. Сколько приседаний сделала Вика на пятый день?

Задание 20 (часть 8) | ЕГЭ 2023 Математика (база) | Задачи на движение по воде

Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки равна 6 км/ч?

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу ОГЭ 2024, Математика, 9 класс, Демонстрационный вариант, Проект — fileskachat.com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу

Источник: obuchalka.org

От пристани против течения реки отправилась моторная лодка собственная скорость которой

С прошлого года, как и с позапрошлого, и позапозапрошлого демо вариант по математике не изменился.

Самое важное из указанного в демо варианте ОГЭ по математике то, что все задания, используемые для составления экзаменационных вариантов, размещены в открытом банке заданий ОГЭ на сайте ФИПИ . Если вы прорешаете все задания из открытого банка заданий ФИПИ, вы автоматически готовы сдать ОГЭ на пятерку. Итак, перейдем непосредственно к демо варианту.

Справочные материалы по математике

К этим справочным данным будет доступ и у вас на ОГЭ, заучивать их не нужно, нужно уметь ими пользоваться.

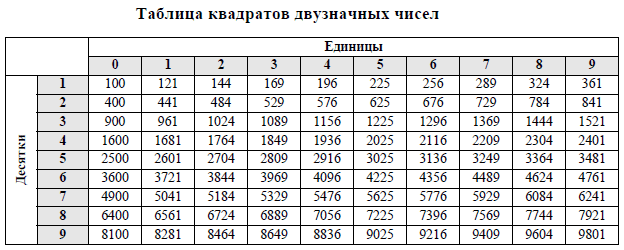
Инструкция по выполнению работы

Экзаменационная работа состоит из двух частей, включающих в себя 25 заданий. Часть 1 содержит 19 заданий, часть 2 содержит 6 заданий с развёрнутым ответом.

На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Ответы к заданиям 7 и 13 запишите в бланк ответов № 1 в виде одной цифры, которая соответствует номеру правильного ответа.

Для остальных заданий части 1 ответом является число или последовательность цифр. Ответ запишите в поле ответа в тексте работы, а затем перенесите в бланк ответов № 1. Если получилась обыкновенная дробь, ответ запишите в виде десятичной.

Решения заданий части 2 и ответы к ним запишите на бланке ответов № 2. Задания можно выполнять в любом порядке. Текст задания переписывать не надо, необходимо только указать его номер.

Все бланки заполняются яркими чёрными чернилами. Допускается использование гелевой или капиллярной ручки. Сначала выполняйте задания части 1. Начать советуем с тех заданий, которые вызывают у Вас меньше затруднений, затем переходите к другим заданиям. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.

При выполнении части 1 все необходимые вычисления, преобразования выполняйте в черновике. Записи в черновике, а также в тексте контрольных измерительных материалов не учитываются при оценивании работы.

Если задание содержит рисунок, то на нём непосредственно в тексте работы можно выполнять необходимые Вам построения. Рекомендуем внимательно читать условие и проводить проверку полученного ответа. При выполнении работы Вы можете воспользоваться справочными материалами, выданными вместе с вариантом КИМ, и линейкой.

Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

После завершения работы проверьте, чтобы ответ на каждое задание в бланках ответов № 1 и № 2 был записан под правильным номером.

Часть 1

Ответами к заданиям 1–19 являются число или последовательность цифр, которые следует записать в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания, начиная с первой клеточки. Если ответом является последовательность цифр, то запишите её без пробелов и других дополнительных символов . Каждый символ пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами.

Прочитайте внимательно текст и выполните задания 1–5.

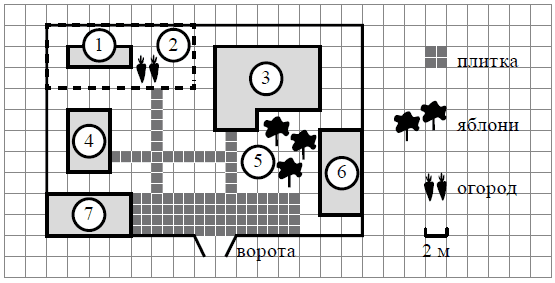
На плане изображено домохозяйство по адресу: с. Авдеево, 3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок справа от ворот находится баня, а слева — гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки.

Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м×1м . Между баней и гаражом имеется площадка площадью 64 кв. м, вымощенная такой же плиткой.

К домохозяйству подведено электричество. Имеется магистральное газоснабжение.

1 Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.

Объекты Жилой дом Сарай Баня Теплица
Цифры 3 4 6 1

2 Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось купить, чтобы выложить все дорожки и площадку перед гаражом?

3 Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.

4 Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками по прямой) в метрах.

5 Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.

Стоимость газа /
электроэнергии

Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления?

6 Найдите значение выражения 1/4 + 0,07

7 На координатной прямой отмечена точка А.

Известно, что она соответствует одному из четырёх указанных ниже чисел. Какому из чисел соответствует точка А?

8 Найдите значение выражения a −7 ⋅(a 5 ) 2 при a = 5.

9 Решите уравнение x 2 + x −12 = 0.

Если уравнение имеет более одного корня, в ответ запишите больший из корней.

10 На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.

11 Установите соответствие между графиками функций и формулами, которые их задают.

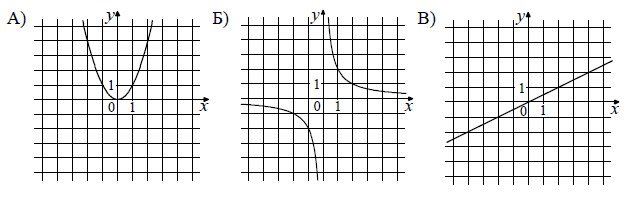
ФОРМУЛЫ
1) y = x 2 2) y = x/2 3) y = 2/х

В таблице под каждой буквой укажите соответствующий номер.

12 Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой tF =1,8tC + 32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует −25 градусов по шкале Цельсия?

13 Укажите решение системы неравенств
х + 2,6 ≤ 0,
х + 5 ≥ 1.

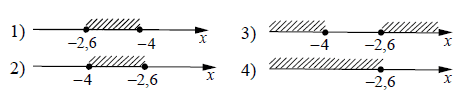
14 Вика решила начать делать зарядку каждое утро. В первый день она сделала 30 приседаний, а в каждый следующий день она делала на одно и то же количество приседаний больше, чем в предыдущий день. За 15 дней она сделала всего 975 приседаний. Сколько приседаний сделала Вика на пятый день?

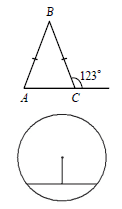
15 В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.

16 Найдите длину хорды окружности радиусом 13, если расстояние от центра окружности до хорды равно 5.

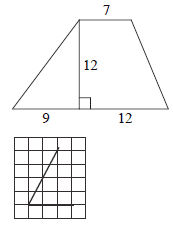
17 Найдите площадь трапеции, изображённой на рисунке.

18 Найдите тангенс острого угла, изображённого на рисунке.

19 Какие из следующих утверждений верны?

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) В любом параллелограмме есть два равных угла.

В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.

Часть 2

При выполнении заданий 20–25 используйте БЛАНК ОТВЕТОВ № 2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.

20 Решите уравнение x 4 = (4x − 5) 2 .

Уравнение x 2 − 4x + 5 = 0 не имеет корней.
Уравнение x 2 + 4x −5= 0 имеет корни −5 и 1 .

21 Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки равна 6 км/ч?

Пусть искомое расстояние равно x км. Скорость лодки при движении против течения равна 4 км/ч, при движении по течению равна 8 км/ч. Время, за которое лодка доплывёт от места отправления до места назначения и обратно, равно ( х /4 + х /8) часа. Из условия задачи следует, что это время равно 3 часам. Составим уравнение:

Решив уравнение, получим x = 8.

22 Постройте график функции $у=frac$ и определите, при каких значениях с прямая y =c имеет с графиком ровно одну общую точку.

Разложим числитель дроби на множители:

x 4 −13x 2 + 36 = (x 2 − 4)(x 2 − 9) = ( x − 2)( x + 2)( x − 3)( x + 3).

При x ≠ −2 и x ≠ 3 функция принимает вид:

её график — парабола, из которой выколоты точки ( −2; −4) и (3; 6).

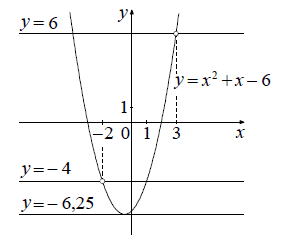
Прямая y = c имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых выколотая. Вершина параболы имеет координаты ( −0,5; −6,25).

Поэтому c = −6,25, c = −4 или c = 6.

Примечание ГДЗответ.ру: к заданиям 23,24 и 25 рисунок на ОГЭ не прилагается, вам нужно сделать его в ходе решения.

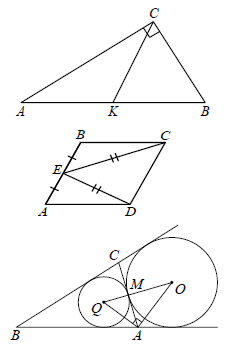
23 В прямоугольном треугольнике ABC с прямым углом C известны катеты: AC = 6, BC=8. Найдите медиану CK этого треугольника.

24 В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник.

Треугольники BEC и AED равны по трём сторонам.
Значит, углы CBE и DAE равны.
Так как их сумма равна 180°, то углы равны 90°.
Такой параллелограмм — прямоугольник.

25 Основание AC равнобедренного треугольника ABC равно 12. Окружность радиусом 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC. Найдите радиус окружности, вписанной в треугольник ABC.

Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC.
Точка касания M окружностей делит AC пополам.
Лучи A Q и AO — биссектрисы смежных углов, значит, угол OAQ прямой.
Из прямоугольного треугольника OAQ получаем: AM 2 = MQ ⋅ MO .
Следовательно,
$QM=frac=frac92=4,5$
Ответ: 4,5.

Проверьте, чтобы каждый ответ был записан рядом с номером соответствующего задания.

Система оценивания ОГЭ по математике 9 класс

Часть 1

За правильный ответ на каждое из заданий 1–19 ставится 1 балл.

Номер Правильный
задания ответ
1 3461
2 23
3 68
4 10
5 500
6 0,32
7 2
8 125
9 3
10 0,2
11 132
12 −13
13 2
14 50
15 57
16 24
17 168
18 2
19 13 31

Критерии оценивания выполнения заданий с развёрнутым ответом

Часть 2

Задание 20. Решите уравнение x 4 = (4x − 5) 2 .

Исходное уравнение приводится к виду:

(x 2 − 4x + 5)(x 2 + 4x − 5)= 0 .

Уравнение x 2 − 4x + 5 = 0 не имеет корней.
Уравнение x 2 + 4x −5= 0 имеет корни −5 и 1 .

Обоснованно получен верный ответ 2
Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учётом дальнейшие шаги выполнены верно — 1 балл
Решение не соответствует ни одному из критериев, перечисленных выше — 0 баллов
Максимальный балл 2

Задание 21. Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость реки равна 2 км/ч, а собственная скорость лодки равна 6 км/ч?

Пусть искомое расстояние равно x км. Скорость лодки при движении против течения равна 4 км/ч, при движении по течению равна 8 км/ч. Время, за которое лодка доплывёт от места отправления до места назначения и обратно, равно ( х /4 + х /8) часа. Из условия задачи следует, что это время равно 3 часам. Составим уравнение:

Решив уравнение, получим x = 8.

Ход решения задачи верный, получен верный ответ — 2 балла
Ход решения верный, все его шаги присутствуют, но допущена описка или ошибка вычислительного характера — 1 балл
Решение не соответствует ни одному из критериев, перечисленных выше — 0 баллов
Максимальный балл 2

Задание 22. Постройте график функции $у=frac$ и определите, при каких значениях с прямая y = c имеет с графиком ровно одну общую точку.

Разложим числитель дроби на множители:

x 4 −13x 2 + 36 = (x 2 − 4)(x 2 − 9) = ( x − 2)( x + 2)( x − 3)( x + 3).

При x ≠ −2 и x ≠ 3 функция принимает вид:

её график — парабола, из которой выколоты точки ( −2; −4) и (3; 6).

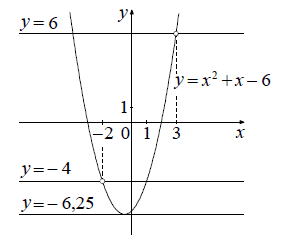
Прямая y = c имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых выколотая. Вершина параболы имеет координаты ( −0,5; −6,25).

Поэтому c = −6,25, c = −4 или c = 6.

Ответ: c=−6,25; c = −4; c = 6.

График построен верно, верно найдены искомые значения параметра — 2 балла
График построен верно, но искомые значения параметра найдены неверно или не найдены — 1 балл
Решение не соответствует ни одному из критериев, перечисленных выше — 0 баллов
Максимальный балл 2

Задание 23. В прямоугольном треугольнике ABC с прямым углом C известны катеты: AC = 6, BC=8. Найдите медиану CK этого треугольника.

Решение.

Ход решения верный, все его шаги выполнены правильно, получен верный ответ — 2 балла
Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения, или допущена одна вычислительная ошибка — 1 балл
Решение не соответствует ни одному из критериев, перечисленных выше — 0 баллов
Максимальный балл 2

Задание 24. В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник.

Треугольники BEC и AED равны по трём сторонам.
Значит, углы CBE и DAE равны.
Так как их сумма равна 180°, то углы равны 90°.
Такой параллелограмм — прямоугольник.

Доказательство верное, все шаги обоснованы — 2 балла
Доказательство в целом верное, но содержит неточности — 1 балл
Решение не соответствует ни одному из критериев, перечисленных выше — 0 баллов
Максимальный балл — 2

Задание 25. Основание AC равнобедренного треугольника ABC равно 12. Окружность радиусом 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC. Найдите радиус окружности, вписанной в треугольник ABC.

Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC.
Точка касания M окружностей делит AC пополам.
Лучи A Q и AO — биссектрисы смежных углов, значит, угол OAQ прямой.
Из прямоугольного треугольника OAQ получаем: AM 2 = MQ ⋅ MO .
Следовательно,
$QM=frac=frac92=4,5$
Ответ: 4,5.

Ход решения верный, получен верный ответ — 2 балла
Ход решения верный, все его шаги присутствуют, но допущена описка или ошибка вычислительного характера — 1 балл
Решение не соответствует ни одному из критериев, перечисленных выше — 0 баллов
Максимальный балл — 2

Баллы и оценка по пятибалльной системе

19 заданий с кратким ответом — по 1 баллу за каждое. 6 заданий с развернутым ответом, по 2 балла максимум за каждое. Всего за тестовую часть можно получить 19 баллов, за развернутую — 12.

0-7 баллов — оценка 2
8-14 баллов (из них минимум 2 балла по геометрии) — оценка 3
15-21 балл (из них минимум 2 балла по геометрии) — оценка 4
22-31 (из них минимум 2 балла по геометрии) — оценка 5

То есть по факту на оценку 4 можно правильно выполнить всего 15 заданий тестовой части, из них 2 задания по геометрии, правда, в профильный класс с таким результатом не возьмут.

Рекомендуемы порог приема в профильные классы для физико-математического профиля — 19 баллов, из них не менее 7 по геометрии (это хотя бы по 1 баллу за каждое задание, ведь их всего 7).

Уже сдали ОГЭ по математике? Пишите в комментариях, какие у вас были задания!

• ОГЭ по математике 2023, все задания ФИПИ с ответами

• Список тем ВПР по математике 8 класс 2023, кодификатор, баллы
• Какие задания были на ОГЭ по математике 23.05. и 24.05 2022 года

• Вы здесь:
• ГИА
• Математика
• Демо вариант ОГЭ по математике 2023 от ФИПИ с ответами

Калькулятор в столбик

• Задание 20 решите уравнение/неравенство/ систему уравнений к ОГЭ по математике ФИПИ*
• Задание 22 постройте график функции к ОГЭ по математике ФИПИ*
• Оформление задач на нахождение средней скорости для ОГЭ по математике
• Задание 21 ОГЭ по математике. Задачи с ответами, ФИПИ
• Задание 12 формулы с ответами к ОГЭ по математике, ФИПИ
• Задания 1-5 практические задачи к ОГЭ по математике ФИПИ 2023 с ответами
• Задание 14 на числовые последовательности (прогрессии) с ответами к ОГЭ по математике ФИПИ
• Задания 6 и 8 ОГЭ по математике ФИПИ с ответами. Найдите значения выражения*
• Задание 10 на теорию вероятности к ОГЭ по математике ФИПИ
• Какие задания были на ОГЭ по математике 23.05. и 24.05 2022 года

Источник: gdzotvet.ru