Во многих задачах интерес представлю не только перемещения материальных точек в пространстве, но и траектории их движения.
Определение
Линию, которую описывает частица при своем движении, называется траекторией движения.
В зависимости от формы траектории механическое движение можно разделить на:
- прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
- и криволинейное перемещение (траектория — кривая линия).
Форма траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми.
При движении точки с постоянным ускорением, которое описывает уравнение:
Уравнение траектории движения
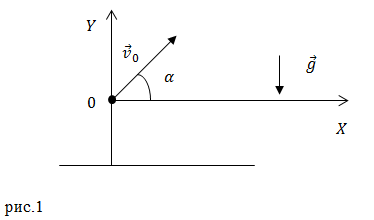
Рассмотрим свободное движение тела около поверхности Земли. Начало координат разместим в точке бросания тела (рис.1). Оси координат направим так, как изображено на рис.1.
Способы описания движения. Траектория. Путь. Перемещение
Тогда уравнение движения тела (1) в проекциях на координатные оси декартовой системы координат принимает вид системы из двух уравнений:
Для того чтобы получить уравнение траектории движения тела ($y=y(x)$) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) $t$ и подставим его в выражение (3), получим:
Выражение (4) это уравнение параболы, проходящей через начало координат. Ее верви направлены вниз, так как коэффициент при $x^2$ меньше нуля.
Вершина этой параболы находится в точке с координатами:
Найти координаты вершины траектории можно при помощи известных правил исследования функций на экстремум. Так, положение максимума функции $y(x)$ определяют, приравнивая к нулю первую производную ($frac$) от нее по $x$.
Обратимость движения
Из представления о траектории можно конкретизировать смысл обратимости механического движения.
Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t $ на $-t$ для всех уравнений.
Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.
Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.
Параметры траектории движения
Положение точек системы отсчета можно определять при помощи разных способов. В соответствии с этими способами описывают и движение точки или тела:
Относительный характер траектории
- Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=rho ,x_2=varphi ,x_3= z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки — это значит указать эти функции: [x_1=x_1left(tright);; x_2=x_2left(tright);; x_3=x_3left(tright)left(6right).]
- При описании движения в векторной форме положение материальной точки задает радиус-вектор ($overline$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $overline$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение: [overline=overlineleft(tright)left(7right).]
- Третьим способом описания движения является описание с помощью параметров траектории.
Путь — это скалярная величина, равная длине траектории.
Если траектория задана, то задачу описания движения сводят к определению закона движения вдоль нее. При этом выбирается начальная точка траектории. Любая другая точка характеризуется расстоянием $s$ по траектории от начальной точки. В таком случае движение описывают выражением:
Пусть по окружности радиуса R равномерно перемещается точка. Закон движения точки по окружности в рассматриваемом методе запишем как:
где $s$ — путь точки по траектории; $t$ — время движения; $A$ — коэффициент пропорциональности. Известными являются окружность и точка начала движения. Отсчет положительных величин $s$ совпадает с направлением перемещения точки по траектории.
Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.
Примеры задач с решением
Задание: Точка движется в плоскости XOY из начала координат со скоростью $overline=Aoverline+Bxoverline , $где $overline$, $overline$ — орты осей X и Y; $A$,B — постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. textit<>
Решение: Рассмотрим уравнение изменения скорости частицы:
[overline=Aoverline+Bxoverline left(1.1right).]
Из этого уравнения следует, что:
Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):
Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:
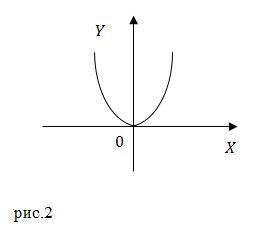
Задание: Движение материальной точки в плоскости описывает система уравнений: $left< begin x=At. \ y=At(1+Bt) end right.$, где $A$ и $B$ — положительные постоянные. Запишите уравнение траектории точки.
Решение: Рассмотрим систему уравнений, которая задана в условии задачи:
Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:
Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:
Ответ: $y=x+fracx^2$

проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Остались вопросы?
Здесь вы найдете ответы.
Источник: www.webmath.ru
Форма траектории и ее практическое значение
Форма траектории зависит от величины угла возвышения. С увеличением угла возвышения высота траектории и полная горизонтальная дальность полета пули (гранаты) увеличиваются, но это происходит до известного предела. За этим пределом высота траектории продолжает увеличиваться, а полная горизонтальная дальность начинает уменьшаться (рис. 4.14).
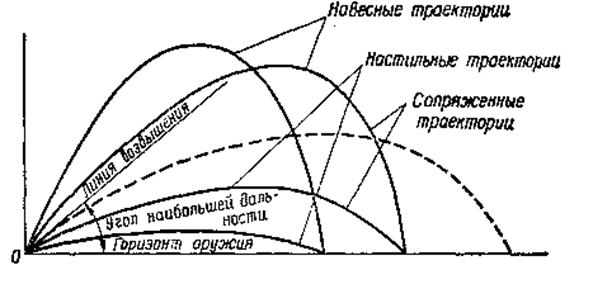
Рис. 4.14. Угол наибольшей дальности, настильные, навесные и сопряженные траектории
Угол возвышения, при котором полная горизонтальная дальность полета пули (гранаты) становится наибольшей, называется углом наибольшей дальности. Величина угла наибольшей дальности для пуль различных видов оружия составляет около 35°.
Траектории, получаемые при углах возвышения, меньших угла наибольшей дальности, называются настильными. Траектории, получаемые при углах возвышения, больших угла наибольшей дальности, называются навесными.
При стрельбе из одного и того же оружия (при одинаковых начальных скоростях) можно получить две траектории с одинаковой горизонтальной дальностью: настильную и навесную. Траектории, имеющие одинаковую горизонтальную дальность при разных углах возвышения, называются сопряженными.
При стрельбе из стрелкового оружия и гранатометов используются только настильные траектории. Чем настильнее траектория, тем на большем протяжении местности цель может быть поражена с одной установкой прицела (тем меньшее влияние на результаты стрельбы оказывают ошибки в определении установки прицела); в этом заключается практическое значение настильной траектории.
Настильность траектории характеризуется наибольшим ее превышением над линией прицеливания. При данной дальности траектория тем более настильна, чем меньше она поднимается над линией прицеливания. Кроме того, о настильности траектории можно судить по величине угла падения: траектория тем более настильна, чем меньше угол падения.
Настильность траектории влияет на величину дальности прямого выстрела, поражаемого, прикрытого и мертвого пространства
Выстрел, при котором траектория не поднимается над линией прицеливания выше цели на всем своем протяжении, называется прямым выстрелом (рис. 4.15).
Рис. 4.15. Прямой выстрел
В пределах дальности прямого выстрела в напряженные моменты боя стрельба может вестись без перестановки прицела, при этом точка прицеливания по высоте, как правило, выбирается на нижнем краю цели.
Дальность прямого выстрела зависит от высоты цели и настильности траектории. Чем выше цель и чем настильнее траектория, тем больше дальность прямого выстрела и тем на большем протяжении местности цель может быть поражена с одной установкой прицела.
Дальность прямого выстрела можно определить по таблицам путем сравнения высоты цели с величинами наибольшего превышения траектории над линией прицеливания или с высотой траектории.
При стрельбе по целям, находящимся на расстоянии, большем дальности прямого выстрела, траектория вблизи ее вершины поднимается выше цели и цель на каком-то участке не будет поражаться при той же установке прицела. Однако около цели будет такое пространство (расстояние), на котором траектория не поднимается выше цели и цель будет поражаться ею.
Расстояние на местности, на протяжении которого нисходящая ветвь траектории не превышает высоты цели, называется поражаемым пространством (глубиной поражаемого пространства).
Глубина поражаемого пространства (рис. 4.16) зависит от высоты цели (она будет тем больше, чем выше цель), от настильности траектории (она будет тем больше, чем настильнее траектория) и от угла наклона местности (на переднем скате она уменьшается, на обратном скате — увеличивается).
Глубину поражаемого пространства (Ппр) можно определить по таблицам превышения траекторий над линией прицеливания путем сравнения превышения нисходящей ветви траектории на соответствующую дальность стрельбы с высотой цели, а в том случае, если высота цели меньше 1/3 высоты траектории,- по формуле тысячной
где: Ппр — глубина поражаемого пространства в метрах; Вц — высота цели в метрах; θс — угол падения в тысячных.
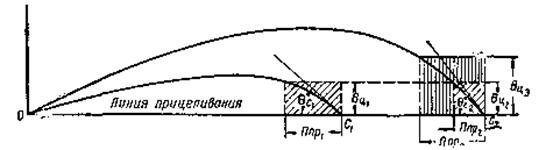
Рис. 4.16. Зависимость глубины поражаемого пространства от высоты цели и настильности траектории (угла падения)
В том случае, когда цель расположена на скате или имеется угол места цели, глубину поражаемого пространства определять вышеуказанными способами, при этом полученный результат необходимо умножить на отношение угла падения к углу встречи.
Величина угла встречи зависит от направления ската: на встречном скате угол встречи равен сумме углов падения и ската, на обратном скате — разности этих углов. При этом величина угла встречи зависит также от угла места цели: при отрицательном угле места цели угол встречи увеличивается на величину угла места цели, при положительном угле места цели — уменьшается на его величину.
Поражаемое пространство в некоторой степени компенсирует ошибки, допускаемые при выборе прицела, и позволяет округлять измеренное расстояние до цели в большую сторону.
Для увеличения глубины поражаемого пространства на наклонной местности огневую позицию нужно выбирать так, чтобы местность в расположении противника по возможности совпадала с продолжением линии прицеливания.
Пространство за укрытием, не пробиваемым пулей, от его гребня до точки встречи называется прикрытым пространством (рис. 4.17). Прикрытое пространство будет тем больше, чем больше высота укрытия и чем настильнее траектория.
Часть прикрытого пространства, на котором цель не может быть поражена при данной траектории, называется мертвым (непоражаемым) пространством. Мертвое пространство будет тем больше, чем больше высота укрытия, меньше высота цели и настильнее траектория. Другую часть прикрытого пространства, на которой цель может быть поражена, составляет поражаемое пространство.
Глубину прикрытого пространства (Пп) можно определить по таблицам превышения траекторий над линией прицеливания. Путем подбора отыскивается превышение, соответствующее высоте укрытия и дальности до него. После нахождения превышения определяется соответствующая ему установка прицела и дальность стрельбы. Разность между определенной дальностью стрельбы и дальностью до укрытия представляет собой величину глубины прикрытого пространства.
Глубина мертвого пространства (Мпр) равна разности прикрытого и поражаемого пространства.
Из пулеметов на станках глубина прикрытого пространства может быть определена по углам прицеливания. Для этого необходимо установить прицел, соответствующий расстоянию до укрытия, и навести пулемет в гребень укрытия. После этого, не сбивая наводки пулемета, отметиться прицелом под основание укрытия. Разница между этими прицелами, выраженная в метрах, и есть глубина прикрытого пространства. При этом предполагается, что местность за укрытием является продолжением линии прицеливания, направленной под основание укрытия.
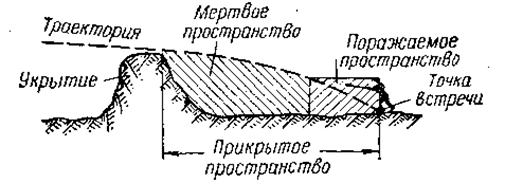
Рис. 4.17. Прикрытое, мертвое и поражаемое пространство
Знание величины прикрытого и мертвого пространства позволяет правильно использовать укрытия для защиты от огня противника, а также принимать меры для уменьшения мертвых пространств путем правильного выбора огневых позиций и обстрела целей из оружия с более навесной траекторией.
Источник: studopedia.ru
Зависит ли форма траекории от выбора тела отсчёта? Приведите примеры

Я долго думал, какие примеры вам привести чтобы они были наглядные.
1. Классический пример. Вы в поезде во время дождя. Если поезд стоит на месте, то капли оставляют на стекле вертикальный след, а во время движения траектория капли наклонная линия. В первом случае тело отсчета неподвижный поезд, во втором-движущийся поезд.
2.Второй пример сложнее. см. фото. Имеется диск, в котором прорезана ложбинка. По этой ложбинке катится шарик. Диск вращается. Если вы будете сидеть на этом диске, то увидите, что мимо вас катится шарик по прямой линии. Если вы сойдете с диска, и будете смотреть со стороны, то увидите, что шарик скатывается и одновременно вращается вместе с диском.
Вы увидите спиральную траекторию.
В первом случае телом отсчета был диск, во втором — земля.
А вообще, чтобы почувствовать траекторию, надо представить себя на теле отсчета.
Остальные ответы
Зависит. Пример: вращающаяся пуля, если за тело отсчета взять пулю, то траектория прямая, если за тело отсчета взять точку на пуле, то траектория спираль (система координат неподвижна) или окружность (система координат движется со скоростью и по траектории пули)
Зависит! Вот смотри: если ты стоиш на пероне и бросаеш монету то относительно тебя траекотрия монеты будет прямая линия вниз, но для человека который едет в поезде, ето будет кривая линия.
Я физику прогуливаю, я не че не знаю =__=
одни сачки. про себя молчу))))
Источник: otvet.mail.ru
Траектория движения тела
Траектория представляет собой своеобразный «след», который оставляет за собой движущееся тело в данной системе отсчета. Она позволяет наблюдателю этой системы отсчета увидеть все точки, которые последовательно проходило тело во время движения. Например, железнодорожный путь указывает траекторию движения поезда, автомобильное шоссе – траекторию движения автомашин. След, оставшийся в небе за летящим самолетом, «рисует» траекторию самолета, лыжня – траекторию лыжника, а любой текст, написанный на листе бумаги – траекторию кончика карандаша или ручки.
Траектория тела в разных системах отсчета
Следует отметить, что траектории движения одного и того же тела в разных системах отсчета могут быть различными. Например, в системе отсчета, связанной с Землей, траектория движения искусственного спутника вокруг Земли – окружность, а в системе отсчета, связанной с Солнцем, — винтовая линия или спираль (рис.1).
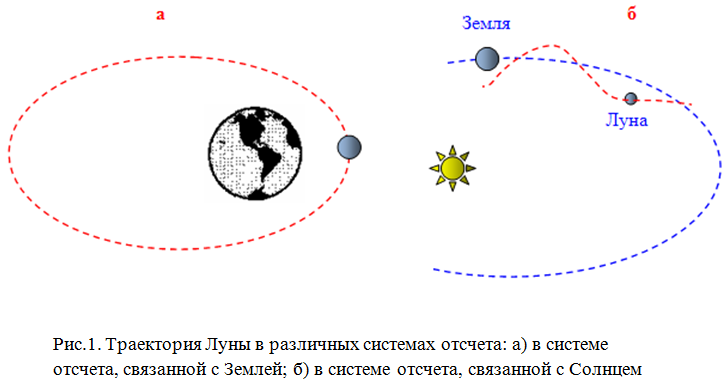
В зависимости от формы траектории механические движения делятся на прямолинейные (траектория – прямая линия) (рис.2, а) и криволинейные (траектория – кривая линия) (рис.2, б).

Определение уравнения траектории движения тела является одной из задач механики.
Примеры решения задач по теме «Траектория»
| Задание | Какова траектория движения точки обода велосипедного колеса при равномерном прямолинейном движении велосипедиста в системах отсчета, жестко связанных: а) с вращающимся колесом; б) с рамой велосипеда; в) с Землей? |
| Ответ | а) в системе отсчета, жестко связанной с вращающимся колесом траектория точки обода велосипедного колеса – точка, так как в этой системе точка обода находится в состоянии покоя; |
б) в системе отсчета, связанной с рамой, траектория точки обода вращающегося колеса – окружность, так как точка обода совершает вращательное движение относительно оси, закрепленной на раме;
в) в системе отсчета, связанной с землей, траектория точки обода вращающегося колеса – циклоида, потому что точка одновременно совершает поступательное и вращательное движения; длина дуги циклоиды равна длине окружности обода колеса.
Источник: ru.solverbook.com
Зависит ли форма траектории, путь и перемещение тела от выбора системы отсчета?

Форма траектории движения одного и того же тела, а также пройденный им путь и перемещение тела существенно зависят от выбора системы отсчета: например, в одной системе отсчета траектория движения тела может быть прямолинейной, а в другой — криволинейной.
- Поставим опыт
- Пример (из книги Галилея)
Смотрите также похожие статьи.
- Путь
Интересное о физике -> Энциклопедия по физике - Перемещение
Интересное о физике -> Энциклопедия по физике - Зависит ли форма траектории, путь и перемещение тела от выбора системы отсчета?
Иллюстрации по физике для 10 класса -> Кинематика - Поставим опыт к теме Зависит ли форма траектории, путь и перемещение тела от выбора системы отсчета?
Учебник по Физике для 10 класса -> Механика - Траектория, путь и перемещение
Учебник по Физике для 10 класса -> Механика - Путь и перемещение
Иллюстрации по физике для 10 класса -> Кинематика - Траектория, путь и перемещение
Иллюстрации по физике для 10 класса -> Кинематика - § 1. Система отсчета. Траектория, путь и перемещение
Учебник по Физике для 10 класса -> Механика - Траектория
Интересное о физике -> Энциклопедия по физике - ФРАНКЛИН БЕНДЖАМИН (1706 — 1790)
Интересное о физике -> Рассказы об ученых по физике - ФАРАДЕЙ МАЙКЛ (1791-1867)
Интересное о физике -> Рассказы об ученых по физике - КУЛОН ШАРЛЬ (1736-1806)
Интересное о физике -> Рассказы об ученых по физике - Пример: тормозной путь автомобиля
Иллюстрации по физике для 10 класса -> Кинематика - Главное в главе 3. Законы сохранения в механике
Учебник по Физике для 10 класса -> Механика - Вопросы и задачи к главе «Кинематика»
Учебник по Физике для 10 класса -> Механика - Как зависят от времени координаты тела, брошенного горизонтально?
Учебник по Физике для 10 класса -> Механика - Вопросы к параграфу § 1. Система отсчета. Траектория, путь и перемещение
Учебник по Физике для 10 класса -> Механика - 1. Наша Галактика — Млечный Путь
Учебник по Физике для 11 класса -> Строение и эволюция Вселенной - ЭЙНШТЕЙН АЛЬБЕРТ (1879-1955)
Интересное о физике -> Рассказы об ученых по физике - ОМ ГЕОРГ СИМОН (1789-1854)
Интересное о физике -> Рассказы об ученых по физике - МАКСВЕЛЛ ДЖЕЙМС КЛЕРК (1831-1879)
Интересное о физике -> Рассказы об ученых по физике - НЬЮТОН ИСААК
Интересное о физике -> Рассказы об ученых по физике - КЕПЛЕР ИОГАНН (1571-1630)
Интересное о физике -> Рассказы об ученых по физике - Вес тела, движущегося с ускорением, направленным вниз
Иллюстрации по физике для 10 класса -> Динамика - Вес тела, движущегося с ускорением, направленным вверх
Иллюстрации по физике для 10 класса -> Динамика - Вес тела, движущегося с ускорением
Иллюстрации по физике для 10 класса -> Динамика - Вес покоящегося тела
Иллюстрации по физике для 10 класса -> Динамика - Как зависит сила тяжести, действующая на тело, от его массы?
Иллюстрации по физике для 10 класса -> Динамика - Перемещение тела за малый промежуток времени
Иллюстрации по физике для 10 класса -> Кинематика - Траектория
Иллюстрации по физике для 10 класса -> Кинематика - От чего зависит суммарная энергия молекул газа?
Учебник по Физике для 10 класса -> Молекулярная физика и термодинамика - Высота, громкость и тембр звука
Учебник по Физике для 10 класса -> Механика - Гармонические колебания
Учебник по Физике для 10 класса -> Механика - Кинетическая энергия
Учебник по Физике для 10 класса -> Механика - Работа силы тяжести
Учебник по Физике для 10 класса -> Механика - Как изменяется импульс тела при взаимодействии?
Учебник по Физике для 10 класса -> Механика - Импульс тела
Учебник по Физике для 10 класса -> Механика - От чего можно оттолкнуться, если вокруг ничего нет?
Учебник по Физике для 10 класса -> Механика - Вопросы к параграфу § 9. Второй закон Ньютона
Учебник по Физике для 10 класса -> Механика - Поставим опыт к теме Масса тела
Учебник по Физике для 10 класса -> Механика - В чем состоит значение гелиоцентрической системы мира?
Учебник по Физике для 10 класса -> Механика - Инерциальные системы отсчета
Учебник по Физике для 10 класса -> Механика - Инерциальные системы отсчета и первый закон Ньютона
Учебник по Физике для 10 класса -> Механика - Поставим опыт к теме Вес тела, движущегося с ускорением
Учебник по Физике для 10 класса -> Механика - Вес покоящегося тела
Учебник по Физике для 10 класса -> Механика - Движение по эллипсу и по параболе (в космосе). Вторая космическая скорость
Учебник по Физике для 10 класса -> Механика - Главное в главе 1. Кинематика
Учебник по Физике для 10 класса -> Механика - Решение к задаче 6. Тормозной путь автомобиля
Учебник по Физике для 10 класса -> Механика - Задача 6. Тормозной путь автомобиля
Учебник по Физике для 10 класса -> Механика - Задача 3. Перемещение при неравномерном движении
Учебник по Физике для 10 класса -> Механика - Поставим опыт к теме По какой траектории движется тело, брошенное горизонтально или под углом к горизонту?
Учебник по Физике для 10 класса -> Механика - По какой траектории движется тело, брошенное горизонтально или под углом к горизонту?
Учебник по Физике для 10 класса -> Механика - Поставим опыт к теме Свободное падение
Учебник по Физике для 10 класса -> Механика - 4. Происхождение Солнечной системы
Учебник по Физике для 11 класса -> Строение и эволюция Вселенной - § 37. Природа тел солнечной системы
Учебник по Физике для 11 класса -> Строение и эволюция Вселенной - Вопросы и задания к параграфу § 35. Размеры солнечной системы
Учебник по Физике для 11 класса -> Строение и эволюция Вселенной - 1. Потенциальная энергия заряда в электростатическом поле
Учебник по Физике для 11 класса -> Электродинамика - Перемещение пробного заряда в поле точечного заряда, при котором работа поля равна нулю
Иллюстрации по физике для 11 класса -> Электродинамика - Перемещение заряда в однородном поле, при котором работа поля равна нулю
Иллюстрации по физике для 11 класса -> Электродинамика - Работа электростатического поля по перемещению заряда
Иллюстрации по физике для 11 класса -> Электродинамика - Млечный Путь
Иллюстрации по физике для 11 класса -> Строение и эволюция Вселенной - Можно ли «увидеть» линии напряженности?
Иллюстрации по физике для 11 класса -> Электродинамика - Млечный путь
Интересное о физике -> Энциклопедия по физике - Тормозной путь автомобиля
Интересное о физике -> Энциклопедия по физике
Механика
Источник: fizikaklass.ru