ЗАДАЧИ СРЕШЕНИЯМИ Основымеханики 1. Равномерное движение 1.1. Первую половину пути турист шел пешком со скоростью 5 км/ч, а вторую половину пути проехал на велосипеде со скоростью 20 км/ч. С какой средней скоростью двигался турист на протяжении всего пути?
Äàíî: v 1 = 5 êì/÷, v 2 = 20 êì/÷, s 1 = s 2 = 2 s . Найти v ñð .
Решение. Обозначим весь путь через s . Средняя скорость переменного движения равна отношению всего пути ко вре- мени движения, т. е. v ñð = s t . Время движения туриста складывается из времени пешего перехода ( t 1 ) и времени езды на велосипеде ( t 2 ). Вычисляем:
| t = | s | ; t = | s | ; v = | s | = | 2 v 1 v 2 | ; | ||||
| t 1 | + t 2 | |||||||||||
| 1 | 2 v 1 | 2 | 2 v 2 | ñð | v 1 + v 2 | |||||||
| v | = | 2 5 20 | êì/÷ = 8 êì/÷. | |||||||||
| ñð | ||||||||||||
| 5 + 20 | ||||||||||||
Ответ: 8 км/ч. 5
Физика. Урок № 6. Кинематика. Минимальная скорость
1.2. Пешеход выходит из пункта À и идет со скоростью 4 км/ч. Спустя 30 мин из этого же пункта выезжает велосипедист со скоростью 12 км/ч. Определить, на каком расстоянии от пункта À и через какой промежуток времени после выхода пешехода велосипедист его догонит.
Äàíî: v 1 = 4 êì/÷; v 2 = 12 êì/÷; t 1 = 2 1 ÷. Найти: t âñòð ; l âñòð .
Решение. Путь, пройденный пешеходом до встречи, l 1 = v 1 t . Велосипедист выезжает позже, поэтому едет до встречи в течение времени t 2 = t âñòð – t 1 .
Следовательно, путь, который проезжает велосипедист до встречи, l 2 = v 2 ( t âñòð – t 1 ). В момент встречи l 1 = l 2 , v 1 t âñòð = v 2 ( t âñòð – t 1 ), откуда находим
| t | = | v 2 t 1 | ; l = l | = | v 1 v 2 t 1 | . | ||||||
| âñòð | v 2 − v 1 | 1 âñòð | v 2 − v 1 | |||||||||
| Вычисляем: | ||||||||||||
| t | = | 12 0,5 | ñ = 0,75 ñ; | l | = | 4 12 0,5 | êì = 3 êì. | |||||
| âñòð | ||||||||||||
| 8 | âñòð | 8 | ||||||||||
| Ответ: t âñòð = 0,75 ñ; | l âñòð | = 3 êì. | ||||||||||
1.3. Эскалатор метро поднимает неподвижно стоящего на нем пассажира в течение 1 мин. По неподвижному эскалатору пассажир поднимается за 3 мин. За какое время поднимается идущий вверх пассажир по движущемуся эскалатору?
Äàíî: t 1 = 1 ìèí; t 2 = 3 ìèí.
Относительность движения более сложные задачи
Найти t.
Решение. Обозначим буквой s длину эскалатора. Тогда скорость его движения v ý = s / t 1 , а скорость пассажира v ï = s / t 2 .
Следовательно, скорость пассажира, идущего по движущемуся эскалатору в том же направлении, равна
| s | s | + | 1 | ||||||||
| v ï + ý = | + | = s | 1 | (1/ìèí), | |||||||
| t 1 | t 2 | ||||||||||
| 3 | |||||||||||
| а время подъема | |||||||||||
| t = | s | = | 3 | ìèí = 45 ñ. | |||||||
| v + | |||||||||||
| 4 | |||||||||||
| ï | ý | ||||||||||
Ответ: t = 45 ñ. 1.4. В течение какого времени пассажир, сидящий у окна поезда, идущего со скоростью 72 км/ч, будет видеть проходящий мимо него встречный поезд, идущий со скоростью 36 км/ч и имеющий длину l = 150 ì?
Äàíî: v 1 = 72 êì/÷ = = 20 ì/ñ, v 2 = 36 êì/÷ = = 10 ì/ñ, l = 150 ì. Найти t . откуда находим t = Ответ: t = 5 ñ.
Решение. Промежуток времени, в течение которого пассажир будет видеть по- езд, равен t = v l ′ , ãäå v R — скорость встречного поезда относительно пассажира. Из закона сложения скоростей следует, что v R = v 1 + v 2 , l 150 , t = 20 + 10 ñ = 5 ñ.
v ð = 0,3 ì/ñ, l = 240 ì,
t = 10 ìèí = = 600 ñ.
Найти: v R; α .
1.5. Лодочник перевозит пассажиров с одного берега на другой за 10 мин по траектории AB (рис. 1). Скорость течения реки 0,3 м/с, ширина реки 240 м. С какой скоростью относительно воды и под каким углом к берегу должна двигаться лодка, чтобы достичь другого берега за указанное время?
Решение. Относительно берега (неподвиж- ной системы отсчета) скорость лод- ки равна v = t l . Эта скорость является суммой двух скоростей: скорости лодки относительно воды v R (скорости относительно подвижной системы отсчета) и скорости реки v ð (скорости подвижной системы отсче- та относительно неподвижной), т. е. v = v R + v ð . Так как по условию задачи скорость лодки относительно берега направлена вдоль AB , то скорость лодки относительно воды v R = 
| l | 240 | 4 | |||
| tg α | = | , tg α | = | = | , α = 53°. |
| v p t | |||||
| 0,3 600 | |||||
| 3 | |||||
| Ответ: v R = 0,5 ì/ñ, α | = 53°. | ||||
1.6. Две лодки движутся навстречу друг другу: первая – по течению реки, вторая — против. Скорости лодок относительно воды 4 м/с и 6 м/с, скорость течения реки 2 м/с. Определить скорости лодок относительно берега и относительно друг друга.
Äàíî: v 1 ′ = 4 ì/ñ, v 2 ′ = 6 ì/ñ, v ð = 2 ì/ñ. Найти: v 1 ; v 2 ; v îòí .
Решение. Скорость лодки относительно берега (неподвижной системы отсчета) равна v = v ð + v ð ′ , откуда v 1 = v 1 ′ + v ð , v 2 = – v 2 ′ + v ð .
Относительная скорость лодок v îòí = v 1 – v 2 . Вычисляя, находим v 1 = 6 ì/ñ; v 2 = – 4 ì/ñ; v îòí = 10 м/с. Ответ: v 1 = 6 ì/ñ; v 2 = – 4 ì/ñ; v îòí = 10 ì/ñ. 2. Равнопеременное движение 2.1. Скорость электропоезда возросла с 18 км/ч до 108 км/ч на пути 875 м. Определить ускорение движения поезда и время ускорения, считая движение равноускоренным.
| Äàíî: | Решение. | |||||||||
| v 1 = 18 êì/÷ = | Используя формулы ускорения при | |||||||||
| = 5 ì/ñ; | равноускоренном движении, находим | |||||||||
| v 2 = 108 êì/÷ = | ||||||||||
| = 30 ì/ñ; | 2 | 2 | ||||||||
| s = 875 ì. | a = | v 2 − v 1 | ; | |||||||
| 2 s | ||||||||||
| Найти: | ||||||||||
| a ; t . | a = | 900 − 25 | ì/ñ 2 | = 0,5 ì/ñ 2 ; | ||||||
| 1750 | ||||||||||
| t = | v 2 − v 1 | ; t = | 30 − 5 | ñ = 50 ñ. | ||||||
| 0,5 | ||||||||||
| a | ||||||||||
Ответ: à = 0,5 ì/ñ 2 , t = 50 ñ.
2.2. Построить график пути переменного движения, если тело начало двигаться из состояния покоя и прошло 6 м за первые 4 с, следующие 3 с находилось в покое и, наконец, прошло еще 8 м за последние 3 с. Найти по графику среднюю скорость движения тела за 10 с.
Äàíî: s 1 = 6 ì; t 1 = 4 ñ; s 2 = 0; t 2 = 3 ñ; s 3 = 8 ì; t 3 = 3 ñ. Найти v ñð .
Решение. Принимаем ось абсцисс за ось времени t , ось ординат — за ось пути s . Для построения графика пути (рис. 2) находим точки по их координатам: O (0; 0), A (4; 6), B (7; 6) è C (10; 14) и соединяем эти точки отрезками прямых.
Ðèñ. 2 Средняя скорость движения тела за время t 1 + t 2 + t 3 = 10 ñ равна v ñð = 14 10 ì ñ = 1,4 ì/ñ. Ответ: 1,4 м/с. 2.3. За время торможения 5 с скорость автомобиля уменьшилась с 72 км/ч до 36 км/ч.
Определить ускорение автомобиля при торможении и длину пути торможения.
| Äàíî: | Решение. | ||||||||||
| v 0 = 72 êì/÷ = | Используя формулы ускорения и | ||||||||||
| = 20 ì/ñ; | пути при равноускоренном движе- | ||||||||||
| v 1 = 36 êì/÷ = | нии, находим | ||||||||||
| =10 ì/ñ; | v 1 | − v 0 | |||||||||
| t = 5 ñ. | a = | ; | |||||||||
| t | |||||||||||
| Найти: | |||||||||||
| a ; s . | a = | 10 − 20 | ì/ñ 2 | = – 2 ì/ñ 2 ; | |||||||
| 5 | |||||||||||
| s = | v 1 2 − v 0 2 | ; s = | 100 − 400 | ì = 75 ì. | |||||||
| − 4 | |||||||||||
| 2 a | |||||||||||
Ответ: a = – 2 ì/ñ 2 ; s = 75 ì. 2.4. Дано уравнение движения тела s = 12 t – t 2 (м). Определить скорость тела в конце пятой секунды движения ( t = 5 ñ).
Äàíî: s = 12 t – t 2 ; t = 5 ñ. Найти v t .
Решение. Из уравнения движения находим, что v 0 = 12 м/с; ускорение равно a = – 2 ì/ñ 2 . Из уравнения скорости движения v t = v 0 + at имеем v t = 12 – 2 t .
Отсюда при t = 5 с мгновенная скорость v t = 12 – 10 = 2 (ì/ñ). Ответ: v t = 2 ì/ñ. 2.5. Автомобиль, движущийся со скоростью 28,8 км/ч, при торможении останавливается в течение 4 с. Считая движение автомобиля равнопеременным, найти уравнение мгновенной скорости, построить график скорости и по графику определить скорость автомобиля в конце третьей секунды от начала отсчета времени. Написать уравнение движения автомобиля.
Äàíî: v 0 = 8 ì/ñ; v t = 0; t = 4 c. Найти v 3 .
Решение. Из условия задачи следует, что v 0 = 8 ì/ñ, v t = 0 è t = 4 с. Найдем ускорение автомобиля при торможе- íèè:
| a = | v t − v 0 | 0 − 8 | 2 | 2 |
| = | ì/ñ | = – 2 ì/ñ . | ||
| t | 4 |
Запишем уравнение мгновенной скорости движения автомобиля:
| v = 8 – 2 t . | ||||||||||
| Пользуясь уравнением скорости, | ||||||||||
| найдем координаты двух произволь- | ||||||||||
| ных точек (например, при t = 0 v = 8; | ||||||||||
| ïðè t = 4 ñ v = 0) и по найденным | ||||||||||
| точкам построим прямую, которая яв- | ||||||||||
| ляется графиком скорости равнопере- | ||||||||||
| менного движения (рис. 3). Из графи- | ||||||||||
| ка следует, что скорость автомобиля в | ||||||||||
| конце третьей секунды v 3 = 2 ì/ñ. Óðàâ- | ||||||||||
| Ðèñ. 3 | нение движения автомобиля: | |||||||||
| s = 8 t – t 2 . | ||||||||||
Ответ: v 3 = 2 ì/ñ, s = 8 t – t 2 . 2.6. Через сколько секунд от начала отсчета времени тело остановится, если уравнение движения тела s = 40 t – 0,1 t 2 (ì)?
| Äàíî: | Решение. |
| s = 40 t – 0,1 t 2 ; | Тело остановится, если скорость |
| v t = 0. | его окажется равной нулю. Из урав- |
| Найти | нения движения найдем начальную |
| t . | скорость и ускорение: v 0 = 40 ì/ñ, |
| a = – 0,2 ì/ñ 2 . Запишем уравнение |
скорости: v = 40 – 0,2 t . Положим v = 0 и решим уравнение относительно t : 0,2 t = 40; t = 200 с. Через 200 с тело остановится. Ответ: t = 200 ñ.
3. Свободное падение 3.1. В свободно падающей кабине свободно падает шарик. С каким ускорением падает шарик относительно кабины? относительно поверхности Земли?
Решение. Относительно кабины шарик падает с нулевым ускорением, так как при одинаковых физических условиях в случае свободного падения все тела имеют одинаковое ускорение. Шарик и кабина падают с ускорениями, равными 9,8 м/с 2 , и разность ускорений равна нулю. Относительно поверхности Земли шарик падает с ускорением 9,8 м/с 2 . 3.2. Какую начальную скорость надо сообщить ракете, расположенной на поверхности Луны, чтобы она при вертикальном подъеме удалилась от Луны на 200 км? Ускорение свободного падения на Луне 1,6 м/с 2 .
| Äàíî: | Решение. | ||
| H = 200 êì = | Из формулы v 0 = | 2 g Ë H находим | |
| = 200 000 ì; | |||
| g Ë = 1,6 ì/ñ 2 . | v 0 | = 2 1,6 200 000 | ì/ñ = 800 ì/ñ. |
| Найти | |||
| v 0 . | |||
Ответ: v 0 = 800 ì/ñ. 3.3. С высоты 80 м над поверхностью Луны тело свободно падает в течение 10 с. Определить ускорение свободного падения на Луне.
| Äàíî: | Решение. | |||||||
| H = 80 ì; | Высота, с которой свободно пада- | |||||||
| t = 10 ñ. | ет тело, вычисляется по формуле | |||||||
| Найти | H = | g Ë t | 2 | , откуда | ||||
| g Ë . | ||||||||
| 2 | ||||||||
| 2 H | 2 80 | |||||||
| g | = | , g | = | ì/ñ 2 = 1,6 ì/ñ 2 . | ||||
| t 2 | ||||||||
| Ë | Ë | 100 | ||||||
Ответ: g Ë = 1,6 ì/ñ 2 .
4. Кинематика вращательного движения 4.1. Ведущее колесо электровоза диаметром 1,2 м делает 300 об/мин. С какой скоростью движется поезд, ведомый электровозом?
Äàíî: D = 1,2 ì; f = 300 îá/ìèí = 5 ñ –1 . Найти v . Ответ: v = 18,9 ì/ñ.
Решение. Согласно формуле скорости вращательного движения находим v = 2π Rf = π Df ; v = 3,14æ1,2 ìæ5 ñ –1 = = 18,9 ì/ñ.
4.2. Искусственный спутник совершает облет Земли по круговой орбите за 1 ч 30 мин. С какой угловой скоростью движется спутник?
| Äàíî: | Решение. | ||||||
| T = 5400 ñ. | Из формулы периода вращения | ||||||
| 2π | |||||||
| Найти | |||||||
| ω . | T = ω | находим | |||||
| ω | = 2π | = | 2 | ðàä | d 0,0012 ðàä/ñ. | ||
| 5400 | ñ | ||||||
| T | |||||||
| Ответ: ω | d 0,0012 ðàä/ñ. | ||||||
4.3. Шкив электромотора диаметром 0,2 м делает 12 000 оборотов за 10 мин. Определить период и частоту вращения, линейную и угловую скорости точек, лежащих
| на ободе шкива. | ||||||
| Äàíî: | Решение. | |||||
| R = 0,1 ì; | Запишем формулы, описывающие | |||||
| n = 12 000; | движение точек (тела) по окружности: | |||||
| t = 600 ñ. | T = | t | è f = | n | — период и частота | |
| Найти: | ||||||
| n | ||||||
| t | ||||||
| T ; f ; v ; ω . | вращения, v = 2π Rf è ω = 2π f — ëè- | |||||
нейная и угловая скорости.
Источник: studfile.net
Определение пройденного кораблем расстояния
Единицы длины и скорости в навигации
Основной единицей длины в навигации является морская миля. Морская миля — длина одной минуты дуги меридиана эллипсоида: ∆1’m = M * arc 1′ = 1852,3 — 9,3 * cos2φ; М — радиус кривизны меридиана эллипсоида.
Таким образом, морская миля — величина переменная, которая зависит от широты места и составляет I843 метра на экваторе и 1861,6 метра на полюсе. Использовать в качестве единицы длины переменную величину крайне неудобно.
В 1931 году в качестве единицы длины была принята стандартная миля, равная длине одной минуты дуги меридиана эллипсоида в широте 44° 18′ и составляющая 1852 метра. Отклонение длины стандартной мили не превышает 0,5% от экстремальных значений длины одной минуты дуги меридиана на экваторе и полюсе и находится в пределах точности корабельных измерителей скорости и пройденного расстояния.
В настоящее время термин стандартная миля практически вышел из употребления и заменен термином — морская миля. Кабельтов — одна десятая часть морской мили = 185,2 метра.
Основной единицей скорости в навигации является узел — скорость, равная одной морской миле в час.
При решении некоторых задач кораблевождения применяется единица скорости — 1 кабельтов в минуту. Для перехода от скорости в узлах к скорости и каб/мин используется соотношение:
Скорость в узлах / 6 = скорость в каб/мин.
Например, если скорость корабля 18 узлов, то он проходит 18 морских миль в час или 18/6 = 3 кабельтова в минуту.
Скорость корабля
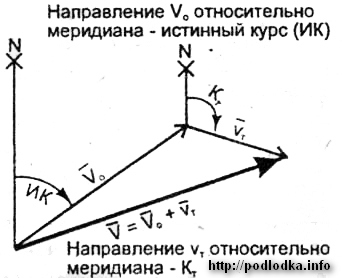Перемещение корабля относительно земной поверхности (морского дна) происходит под воздействием собственных движителей, а так же под влиянием внешних факторов — ветра и течения.
Скорость корабля относительно поверхности воды под воздействием движителей и ветра — относительная скорость (V0). Под воздействием течения корабль вместе с водными массами перемещается относительно морского дна со скоростью течения (Vт). Таким образом, под воздействием собственных движителей, ветра и течения корабль перемешается относительно морского дна со скоростью V, которая называется абсолютной или путевой.
Направление вектора абсолютной или путевой скорости корабля V относительно меридиана — путь корабля — линия его фактического перемещения.
Измерители скорости на корабле
Лаг — прибор для измерения скорости на корабле:
— относительный — измеряет V0;
— абсолютный — измеряет V.
По физическим принципам измерения относительной скорости лаги подразделяются на:
— гидродинамические: Рп = f (V0), Рп — полное давление набегающего потока волы;
— индукционные: Е = f (V0), Е — э.д.с, образующаяся в проводнике, при его перемещении в магнитном поле.
Конструктивно относительные лаги выполнены в виде двух основных блоков:
— измерения скорости V0;
— вычисления пройденного кораблем расстояния So (счетчик пройденного расстояния)
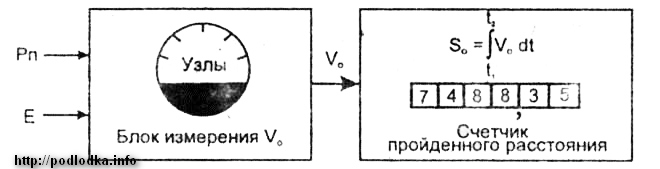Расстояние, пройденное кораблем, вычисляется по показаниям счетчика пройденного расстояния как разность двух последовательных отсчетов лага: рол = ОЛ2-ОЛ1
Скорость, снимаемая с приборов относительного лага — Vл — лаговая скорость, содержит инструментальные и методические погрешности и в общем случае не равна относительной скорости корабля V0. Расстояние, вычисленное по показаниям счетчика лага (рол), также содержит погрешность.
Понятие об определении поправок лага
Ежегодно на кораблях ВМФ проводится комплекс мероприятий, называемый определение маневренных элементов. Одной из его составляющих является определение относительной скорости Vo, соответствующей частоте работы движителей No и поправок относительного лага — ∆Л%.
Для определения скорости используются специально оборудованные полигоны, называемые мерными линиями, на которых некоторым образом создается эталонное расстояние Sэ, например, с помощью створных знаков, как показано на рисунке:
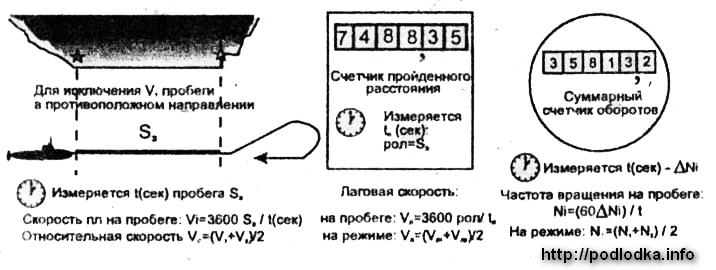По результатам измерений на мерной линии вычисляются:
— относительная скорость корабля Vo на основных режимах движения (СПХ, ПХ, СХ, MX. СМХ);v — соответствующая ей частота вращения движителей по показаниям суммарных счетчиков оборотов — N0,
— лаговая скорость Vn по показаниям счетчика пройденного расстояния лага;
— коэффициент относительного лага: Кл = Vo / Vn;
Если Кл >1 (V0 >Vл) — лаг «отстает» — поправка лага ∆Л% — положительная; Если Кл
- Главная /
- Обучение /
- Практическая навигация /
- Определение пройденного кораблем расстояния
Смотрите также
Подводная лодка «Святой Георгий»
Лодка
Старый хрен
Добавить комментарий
Ваши комментарии не должны содержать призывов к насилию, разжиганию межнациональной розни и экстремизму, оскорблений, нецензурной лексики, а также сообщений рекламного характера. Все комментарии, не отвечающие этим требованиям, будут модернизироваться или удаляться.
Войдите через социальные сети:
Источник: podlodka.info
Подготовка к егэ. Относительность движения
Все кинематические понятия: траектория, координаты, путь, перемещение, скорость – имеют определенную форму и численные значения в одной выбранной системе отсчета. При переходе от одной системы отсчета к другой указанные величины могут измениться. В этом состоит так называемая относительность движения, и в этом смысле механическое движение всегда относительно. Например: Катится колесо по поверхности Земли. (Рис.1)
Точка А обода колеса относительно координатной системы Х 1 О 1 У 1 движется по окружности, проходя за время одного оборота путь, равный длине этой окружности. Но относительно системы
ХОУ, связанной с поверхностью Земли, траекторией точки А является более сложная кривая А 1 А 2 А 3 , называемая циклоидой. За этот ж интервал времени точка А проходит путь, равный длине этой кривой.
Пример 2: Представьте себе пассажира в движущемся равномерно относительно Земли вагоне, выпускающего из рук мяч. Он видит, как мяч падает относительно вагона вертикально вниз с ускорением g. ( Рис.2)
Свяжем с вагоном систему координат Х 1 О 1 У 1 . В этой системе координат за время падения мяч пройдет путь AD = h, и пассажир видит, что мяч упал на пол со скоростью V 1 , направленной вертикально вниз. Ну а что увидит наблюдатель, находящийся на неподвижной платформе, с которой связана система координат ХОУ? Он заметит, что траекторией мяча является парабола AD и мяч упал со скоростью V 2 , направленной под углом к горизонту. И так мы отмечаем, что наблюдатели в системах Х 1 О 1 У 1 ХОУ обнаруживают различные по форме траектории, скорости, пройденные пути при движении одного тела – мяча.
Связь координат точки в системах отсчета, движущихся друг относительно друга, описывается преобразованиями Галилея. ( Формула сложения скоростей):
Скорость тела относительно неподвижной системы отсчета равна геометрической сумме скорости тела относительно подвижной системы и скорости самой подвижной системы отсчета.
абсолютная скорость тела ( скорость тела
относительно неподвижной системы отсчета)
относительна скорость ( скорость тела относительно подвижной системы отсчета)
переносная скорость ( скорость самой подвижной системы относительной неподвижной системы отсчета.
Принцип относительности Галилея. Все инерциальные системы равноправны. Это проявляется в том, что законы механики в них записываются одинаково.
Инерциальные системы отсчета – системы отсчета, которые двигаются равномерно, прямолинейно относительно друг друга.
Относительная скорость двух тел.
Рассмотрим два тела А и В, имеющих в системе отсчета К скорости . Найдем скорость движения тела В относительно тела А. Для этого свяжем систему отсчета К 1 с телом А (рис). Тогда искомая относительная скорость есть скорость тела относительно системы К 1
Воспользуемся далее законом сложения скоростей. Для данного случая скорость тела В относительно системы отсчета К представляет собой абсолютную скорость: = V A
Скорость тела А в системе отсчета К — это переносная скорость. Наконец, скорость — это есть относительная скорость: =V oTH Согласно закону сложения скоростей (1.30.8) имеем
Или скорость движения тела В относительно тела А равна разности скоростей этих двух тел. Она не зависит от системы отсчета. В любой системе отсчета, движущейся со скоростью U относительно системы отсчета К,
Преобразования Галилея. Согласно этим представлениям расстояния между телами одинаковы во всех системах отсчета и течение времени не зависит от систем отсчета.
§ 1.31. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Из всех задач на относительность движения мы будем в основном решать такие, которые связаны с законом сложения скоростей. Для этого удобно использовать понятия абсолютного, относительного и переносного движений.
Решая задачу, следует выбрать две системы координат и одну из них условно принять за неподвижную, после чего уяснить, какая скорость будет абсолютной, переносной и относительной. далее надо записать закон сложения скоростей . После этого можно переходить к записи этого закона в проекциях на выбранные направления осей координат. Но можно воспользоваться и геометрическим сложением векторов.