Задание 11. Моторная лодка прошла против течения реки 143 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 12 км/ч. Ответ дайте в км/ч.
Ответ задания: 1
- Все задания варианта
- Наша группа Вконтакте
- Наш канал
Темы раздела
- Вариант 1
- Вариант 1. Задания по ЕГЭ 2018. Математика. И.В. Ященко. 36 вариантов
- Решения заданий по номерам
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 16
- 17
- 18
- 19
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 16
- 17
- 18
- 19
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 17
- 19
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 15
- 17
- 19
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 15
- 17
- 19
- Инструменты ЕГЭиста
- Наш канал
Частичное или полное копирование решений с данного сайта для распространения на других ресурсах,
Найдите скорость теплохода в неподвижной воде, задача 22, ОГЭ 2020
в том числе и бумажных, строго запрещено. Все решения являются собственностью сайта
Источник: self-edu.ru
Найдите скорость течения если скорость лодки в неподвижной воде равна 12

Опубликовано 12.06.2017 по предмету Алгебра от Гость >> Оцени ответ


- Алгебра

- Математика

- Русский язык

- Українська мова

- Информатика

- Геометрия

- Химия

- Физика

- Экономика

- Право

- Английский язык

- География

- Биология

- Другие предметы

- Обществознание

- История

- Литература

- Українська література

- Беларуская мова

- Қазақ тiлi

Показать ещё
Теплоход, скорость которого в неподвижной воде равна 16 км/ч, проходит по течению реки и после
Источник: www.shkolniku.com
Задание 11. ЕГЭ. Моторная лодка прошла против течения реки 143 км и вернулась в пункт отправления


Задание. Моторная лодка прошла против течения реки 143 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 12 км/ч. Ответ дайте в км/ч.
Решение:
Пусть x км/ч – скорость течения реки,
тогда скорость моторной лодки против течения реки равна (12 – x) км/ч,
а скорость моторной лодки по течению реки равна (12 + x) км/ч.
На путь против течения реки моторная лодка затратила 143/(12 – x) ч.,
а на путь по течению реки моторная лодка затратила 143/(12 + x) ч.
Так как на обратный путь (по течению реки) моторная лодка затратила на 6 часа меньше,
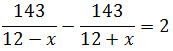
Упростим уравнение, для этого умножим обе части уравнения на (12 – x)·(12 + x), получим
143·(12 + x) – 143·(12 – x) = 2·(12 – x)·(12 + x)
1716 + 143x – 1716 + 143x – 288 + 2x 2 = 0
2x 2 + 286x – 288 = 0
x 2 + 143x – 144 = 0
D = 143 2 – 4·1·(-144) = 21025
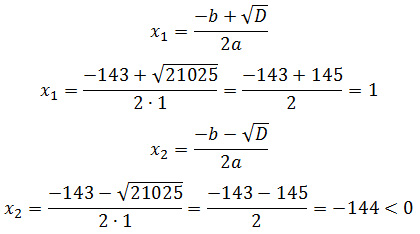
Так как скорость течения реки не может быть отрицательной величиной,
получим ее скорость 1 км/ч.
Ответ: 1
P.S. Для извлечения квадратного корня из числа 21025 можно воспользоваться следующим способом:
Определим, между какими числами лежит результат корня. Для этого разобьем число 21025 на группы по две цифры, начиная справа налево, у нас получилось три группы чисел 2.10.25, т. е. необходимо подбирать числа кратные 100. Результат корня будет лежать между числами 100 и 200, так как
100 2 = 10000 и 200 2 = 40000.
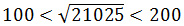
Далее определяем, как число 21025 расположено относительно чисел 10000 или 40000. Получается, что число 21025 расположено ближе к 10000, чем к 40000. Поэтому результат корня будет меньше 150.
Пробуем возводить в квадрат числа 150, 140, … Это умножение легко выполнить в столбик.
150 2 = 150·150 = 22500
140 2 = 140·140 = 19600
Можно сделать вывод, что
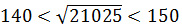
Так как число 21025 оканчивается цифрой 5, то в квадрат необходимо возводить числа, расположенные между 120 и 130 и оканчивающиеся на 5, такое число одно:
145 2 = 145·145 = 21025
Источник: bezikev.ru