Найдите скорость лодки в неподвижной воде если скорость течения равна 3

Задачи, в которых сказано, что моторная лодка прошла и вернулась обратно (по течению-против течения) обычно сводятся к двум случаям: сравнивается время на путь против течения и по течению либо известно общее время, затраченное на путь туда и обратно.

При этом скорость лодки по течению реки равна сумме скоростей: собственной скорости лодки и скорости течения, скорость лодки против течения равна разности этих скоростей.

За x обычно принимают неизвестную величину, которую требуется найти (собственную скорость лодки или скорость течения реки).

Если время выражено в минутах, то его следует перевести в часы:

Моторная лодка прошла против течения реки 208 км и вернулась в пункт отправления, затратив на обратный путь на 5 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5 км/ч.

Пусть скорость лодки в неподвижной воде равна x км/ч.

motornaya-lodka-proshla-i-vernulas-obratno

Составим уравнение и решим его:

[ frac{{208^{^{backslash (x + 5)} } }}{{x - 5}} - frac{{208^{^{backslash (x - 5)} } }}{{x + 5}} = 5^{backslash (x^2 - 25)} ]

[ frac{{208(x + 5) - 208(x - 5) - 5(x^2 - 25)}}{{(x - 5)(x + 5)}} = 0 ]

[ frac{{ - 5x^2 + 2205}}{{(x - 5)(x + 5)}} = 0__left| {:5} right. Leftrightarrow left{ begin{array}{l} x^2 - 441 = 0; \ (x - 5)(x + 5) ne 0 \ end{array} right. ]

x1=21 или x2=-21 — не удовлетворяет условию задачи, так как скорость не может быть отрицательным числом.

Скорость лодки в неподвижной воде равна 21 км/ч.

Моторная лодка прошла по течению 24 км и вернулась обратно, затратив на обратный путь на 20 минут меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 3 км/ч.

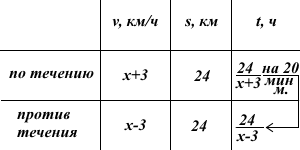
motornaya-lodka-proshla

Пусть собственная скорость лодки в неподвижной воде (то есть собственная скорость лодки) равна x км/ч.

Время переводим из минут в часы:

motornaya-lodka-proshla-po-techeniyu

Составим уравнение и решим его:

[ frac{{24^{backslash 3(x + 3)} }}{{x - 3}} - frac{{24^{backslash 3(x - 3)} }}{{x + 3}} = frac{{1^{backslash (x^2 - 9)} }}{3} ]

[ frac{{72(x + 3) - 72(x - 3) - (x^2 - 9)}}{{(x - 3)(x + 3)}} = 0 ]

[ frac{{72x + 216 - 72x + 216 - x^2 + 9}}{{(x - 3)(x + 3)}} = 0 ]

[ frac{{ - x^2 + 441}}{{(x - 3)(x + 3)}} = 0__left| { cdot ( - 1)} right. Leftrightarrow ]

[ Leftrightarrow left{ begin{array}{l} x^2 - 441 = 0; \ x ne 3,x ne - 3 \ end{array} right. ]

x1=21 или x2=-21 не удовлетворяет условию задачи.

Скорость лодки в неподвижной воде равна 21 км/ч.

Баржа прошла по течению реки 88 км и, повернув обратно, прошла ещё 72 км, затратив на весь путь 10 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.

Читайте также:  Как работает балластная система на подводной лодке

Пусть x км/ч собственная скорость баржи.

barzha-proshla-po-techeniyu-reki

Составим и решим уравнение:

[ frac{{88}}{{x + 5}} + frac{{72}}{{x - 5}} = 10__left| {:2} right. ]

[ frac{{44^{backslash (x - 5)} }}{{x + 5}} + frac{{36^{backslash (x + 5)} }}{{x - 5}} = 5^{backslash (x^2 - 25)} ]

[ frac{{44(x - 5) + 36(x + 5) - 5(x^2 - 25)}}{{(x - 5)(x + 5)}} = 0 ]

[ frac{{44x - 220 + 36x + 180 - 5x^2 + 125}}{{(x - 5)(x + 5)}} = 0 ]

[ frac{{ - 5x^2 + 80x + 85}}{{(x - 5)(x + 5)}} = 0__left| {:( - 5)} right. Leftrightarrow ]

[ Leftrightarrow left{ begin{array}{l} x^2 - 16x - 17 = 0; \ x ne 5,x ne - 5 \ end{array} right. ]

x1=17 или x2=-1 — не удовлетворяет условию задачи.

Значит собственная скорость баржи равна 17 км/ч.

В следующий раз рассмотрим задачи, в которых теплоход (баржа) после стоянки возвращается обратно.

Источник: www.algebraclass.ru

Найдите скорость лодки в неподвижной воде если скорость течения равна 3

Привет Лёва Середнячок

Umnik1234

Моторная лодка прошла против течения реки 187 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 3 км/ч. Ответ дайте в км/ч.

Ответ проверен экспертом

3 (5 оценок)

milan175

milan175 7 лет назад

Светило науки — 2078 ответов — 0 раз оказано помощи

х км/ч — скорость лодки в неподвижной воде
(х-3) км/ч — скорость против течения реки
(х+3) км/ч — скорость по течению реки
[tex] frac — frac =6 [/tex]
187(х+3)-187(х-3)=6(х-3)(х+3)
187х+561-187х+561=6х²-54
-6х²+1176=0 I:(-6)
х²-196=0
х²=196
км/ч- скорость м.лодки в неподвижной воде
— не подходит

Источник: vashurok.com

Найдите скорость лодки в неподвижной воде, если скорость течения равна 3 км/ч. Лодка прошла по течен

ию реки 36 км и вернулась обратно, потратив на весь путь 5 часов.

Ответы на вопрос

Отвечает Калабухов Сергей.

Собственная скорость движения лодки (скорость лодки в неподвижной воде) — Х км/час
Тогда
время=путь/скорость
36/(Х+3)+36/(Х-3)=5
[36*(X-3)+36*(X+3)]-5*(X+3)*(X-3)/(X+3)*(X-3)=0
[(36*X-108+36*X+108)-5*(X^2-3*X+3*X-9)]/(X^2-3*X+3*X-9)=0
72*X-5*X^2+45=0
-5*X^2+72*X+45=0
Решаем квадратное уравнение с помощью дискриминанта
и получаем два корня уравнения: Х1=-0,6; Х2=15
Скорость не может быть отрицательной, поэтому Х=15 км/час
Проверяем:
36/(15+3)+36/(15-3)=5
36/18+36/12=5
2+3=5
Ответ: скорость лодки в неподвижной воде — 15 км/час

Источник: uznavalka.pro

Рейтинг
( Пока оценок нет )
Комментарии0
Загрузка ...
Похожие материалы