Остойчивостью называется способность подводной лодки, выведенной из положения равновесия под воздействием внешних сил, вновь возвращаться в первоначальное положение после прекращения действия этих сил [41]. Таким образом, остойчивость — свойство ПЛ, проявляющееся только при отклонении ее от положения равновесия. Остойчивость, наряду с плавучестью, является важнейшим мореходным качеством ПЛ. Плавучесть обеспечивает возможность равновесия подводной лодки при определенной посадке, а остойчивость — способность сохранять это положение.
Анализ остойчивости подводной лодки производится для надводного и подводного положений, а также для периода погружения и всплытия. Рассматривают также остойчивость в позиционном положении, а для дизельных ПЛ — и с топливом в перегрузку.
При переходе из одного положения в другое остойчивость подводной лодки претерпевает не только количественные, но и качественные изменения.
В надводном положении остойчивость подводной лодки ничем не отличается от остойчивости надводного корабля и представляет остойчивость формы, ибо остойчивость веса при этом, как правило, отрицательна.
Остойчивость. Метацентрическая высота
Обычно подводная лодка остойчива лишь до наклонений определенной величины, причем эти пределы для различных лодок и наклонений в различных плоскостях различны. Поэтому во избежание ошибок сначала проверяют, остойчива ли лодка хотя бы при малых наклонениях от положения равновесия, а затем исследуют ее остойчивость на больших наклонениях и определяют пределы остойчивости.
Если подводная лодка остойчива при малых наклонениях из положения равновесия, то говорят, что в этом положении она имеет положительную начальную остойчивость. Нужно сразу же предостеречь от двух возможных ошибок.
Во-первых, не следует считать, что ПЛ обладает какими-то двумя разными видами остойчивости — начальной и на больших наклонениях. Существует единое мореходное качество корабля — остойчивость и различные формы ее проявления, которые исследуются различными методами. При изучении начальной остойчивости на первый план выдвигается противодействие ПЛ начальным отклонениям от положения равновесия, то есть способность сохранения ею этого положения. В соответствии с этим, строго говоря, рассматриваются даже не сами отклонения, а лишь тенденции к ним и реагирование на них находящейся в равновесии подводной лодки.
При исследовании остойчивости на больших наклонениях, наоборот, на первый план выдвигается вопрос о величинах отклонений, до которых ПЛ еще сохраняет способность возвращаться в исходное положение равновесия.
Во-вторых, неверно сводить различие между начальной остойчивостью и остойчивостью при больших наклонениях только к различию математических методов исследования, то есть к использованию в одном случае линейной, а в другом нелинейной теории остойчивости. Как показано выше, различны также и цели исследования.
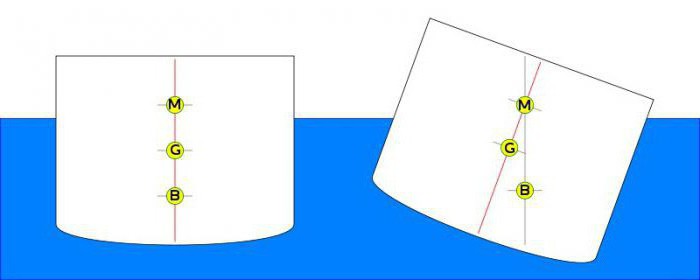
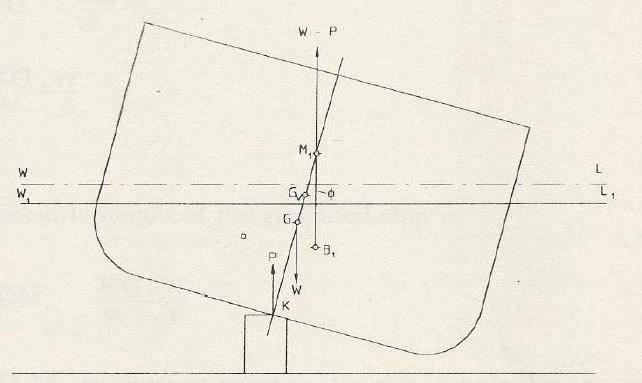
В надводном положении остойчивому положению равновесия соответствует расположение поперечного метацентра m выше центра тяжести лодки G, а неостойчивому — ниже центра тяжести G (рис. 3.2).
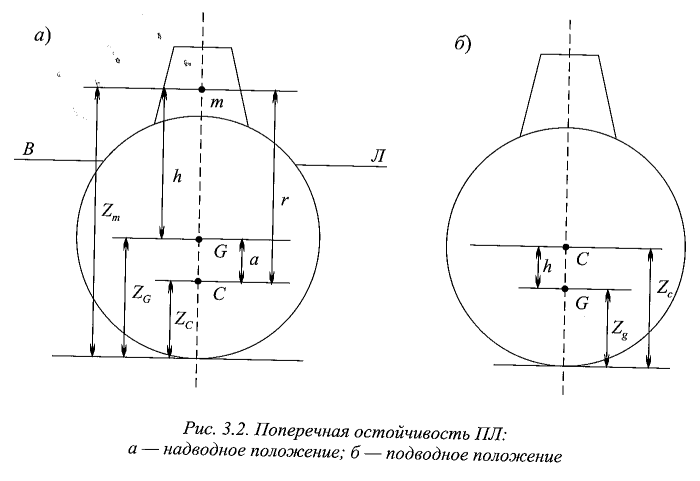
Возвышение метацентра над центром тяжести подводной лодки называется метацентрической высотой. Соответственно, возвышение поперечного метацентра m над центром тяжести лодки G называется поперечной метацентрической высотой h, а возвышение продольного метацентра М над центром тяжести лодки G — продольной метацентрической высотой Н. При отсутствии у лодки крена и дифферента метацентрические высоты h и Н определяются для надводного положения выражениями:
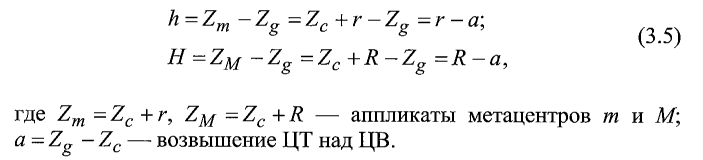
При плавании в погруженном положении действующая ватерлиния отсутствует, метацентрический радиус обращается в ноль, и остойчивость определяется остойчивостью веса. Формулы для погруженного положения принимают вид

Из приведенных соотношений видно, что если в погруженном положении центр тяжести корабля окажется выше центра величины постоянного плавучего объема, то подводная лодка будет обладать отрицательной остойчивостью и перевернется. В связи с этим для возможности плавания в подводном положении необходимо, чтобы ЦВ постоянного плавучего объема располагался выше ЦТ лодки. Наружный непроницаемый корпус, оказывающий существенное влияние на остойчивость ПЛ в надводных положениях, не влияет на ее подводную остойчивость, т.к. сохраняет свою непроницаемость только до погружения подводной лодки. Положение ЦБ в подводном положении определяется в основном прочным корпусом. Поскольку существенное повышение Zc за счет прочного корпуса не представляется возможным, то при проектировании ПЛ необходимо уделять особое внимание рациональному размещению оборудования с целью получения более низкого положения ЦТ.
Минимально допустимые значения метацентрических высот h и Н при нормальных условиях надводного и подводного положений плавания зависят от типа лодки, ее архитектуры и назначения.
Для определения начальной поперечной метацентрической вы-соты подводной лодки в процессе погружения (или всплытия) на основании кривых элементов теоретического чертежа строят так называемую диаграмму начальной остойчивости ПЛ при прерванном погружении (или всплытии). Диаграмма строится в предположении, что ПЛ погружается и всплывает без крена и дифферента.
Независимым параметром при построении диаграммы служит осадка Т.
Погружение (всплытие) рассматривается как прохождение ПЛ ряда последовательных положений равновесия, в каждом из которых она плавает с открытыми кингстонами и закрытыми клапанами вентиляции.
Дата добавления: 2022-01-31 ; просмотров: 201 ;
Источник: edustud.org
Вывод формулы начальной остойчивости
— аппликата центра тяжести тела в положении равновесия, — аппликата центра величины погруженного объема.
Тогда – возвышение центра кривизны М над центром тяжести тела G.
Формула (11.4) выведена для бесконечно малого наклонения, но ее можно использовать и для небольших конечных углов (т.е. ). Тогда формулу можно переписать в виде
1. Формула (11.5) справедлива для любых плавающих тел, в том числе и для водоизмещающих судов любых типов. Начальной остойчивостью судна называется способность находящегося в равновесии судна сопротивляться любому воздействию, вызываемому внешними или внутренними причинами, стремящемуся вывести его из исходного положения равновесия при малых начальных отклонениях. Если наклон происходит только в поперечной плоскости судна, то угол наклона будет называться углом крена, а формула (11.5) носит название метацентрической формулы поперечной остойчивости. Величина , входящая в (11.5), при наклоне судна только в поперечной плоскости судна, называется поперечной или малой метацентрической высотой, величина — малым метацентрическим радиусом, точка М – поперечным метацентром судна. Если наклон происходит в диаметральной плоскости судна, то угол наклона называется углом дифферента, а метацентрическая высота называется продольной или большой.
2. При рассмотрении тела, полностью погруженного в жидкость (подводные аппараты, подводные лодки и т.п.), условия равновесия остаются прежними: вес тела и сила поддержания должны быть равны, а центры приложения этих сил должны располагаться на одной вертикали. Отличие этого случая от рассмотренного ранее состоит в неизменности при наклонении тела положения его центра величины (центр величины и метацентр совпадают). Очевидно, что положение равновесия полностью погруженного тела устойчиво, если центр величины располагается выше центра тяжести (это возвышение оказывается метацентрической высотой для наклонения тела в любой плоскости). Величина восстанавливающего момента, препятствующего наклонению полностью погруженного тела, рассчитывается, как и прежде, по формуле (11.5).
Пример 11.1: На прямоугольном понтоне длины L, ширины B и осадки T в диаметральной плоскости имеется груз веса P. Зная аппликату центра тяжести понтона с грузом , найти выражение для угла крена понтона при смещении груза к борту на расстояние . До перемещения груза углы крена и дифферента понтона равнялись нулю.
Перемещение груза (снятие его из начального положения и перенос в новое) вызывает возникновение пары сил, стремящихся наклонить понтон. Полагая возникающий угол крена небольшим (), кренящий момент этой пары сил равен
Момент пары сил, стремящийся вернуть понтон в исходное положение, рассчитывается по формуле (11.5) как
где — удельный вес воды, V – объем подводной части понтона.
В формуле учтено, что объем подводной части понтона равен произведению его длины, ширины и осадки, а аппликата центра величины погруженного объема равна половине осадки.
Схема сил, действующих на понтон в этой ситуации, изображена на рис. 11.3.
Приравняв кренящий и восстанавливающий моменты, получим уравнение для угла крена понтона:
Вычислим малый метацентрический радиус . Для этого дадим понтону небольшое (край борта не погружается в воду, край днища не выходит из воды) равнообъемное наклонение на угол . Ось поворота делит пополам прямоугольник ватерлинии. В этом случае объемы входящего и выходящего клиньев одинаковы и равны
Расстояние между центрами тяжести клиньев будет .
Подставив полученные значения в формулу для длины дуги, имеем
Теперь вычислим малый (поперечный) метацентрический радиус прямоугольного понтона как
Окончательное выражение для угла крена принимает вид
Пример 11.2: Прямоугольный понтон длины L и ширины B, плавая без крена и дифферента, имеет осадку Т, высоту надводного борта H < T и аппликату центра тяжести .
Осуществим буксировку понтона, приложив силу к точке палубы, расположенной в верхнем углу сечения понтона диаметральной плоскостью. Силу сопротивления воды, возникающую при буксировке понтона с постоянной скоростью, будем полагать равной
где — эмпирический коэффициент, S – площадь наибольшего погруженного поперечного сечения, — скорость буксировки; точка приложения силы сопротивления находится в центре площади S. Найти величину скорости буксировки, при которой начинается заливание палубы понтона. Процесс образования волн не учитывать.
Изобразим понтон в предельном положении, когда край палубы находится на уровне воды (см. рис. 11.4).
Полагая угол дифферента понтона небольшим, запишем выражение для его определения как
Нанесем на рисунок силы, действующие на понтон (сила тяги F, сила сопротивления R, сила веса D и сила поддержания V). Заметим, что крен понтона равен нулю, так как все силы расположены в его диаметральной плоскости. Постоянство скорости буксировки позволяет рассмотреть равновесие системы сил, приложенных к понтону.
Приравнивая нулю проекцию на ватерлинию главного вектора сил, получаем, что величины сил тяги и сопротивления должны быть равными. В таком случае пара этих сил создает момент, стремящийся наклонить понтон. При небольшом угле дифферента () этот момент равен
При выводе формулы полагалось, что при сделанном допущении площадь наибольшего погруженного поперечного сечения равна
Пара сил веса и поддержания создает восстанавливающий момент, равный, согласно формуле (11.5)
Здесь — большая (или продольная) метацентрическая высота понтона. Ее величина рассчитывается по формуле, структура которой аналогична выведенной выше для малой метацентрической высоты, т.е.
Приравняв кренящий и восстанавливающий моменты, получим выражение для интересующей нас скорости буксировки
Пример 11.3: Подводная лодка (ПЛ), двигаясь в подводном положении в горизонтальной плоскости с постоянной по величине скоростью , совершает циркуляцию радиуса (см. рис. 11.5).
Найти выражение для угла крена ПЛ, возникающего при выполнении этого маневра, если известны ее водоизмещение D, поперечная метацентрическая высота h=CG и расстояние от точки приложения силы бокового давления до центра тяжести OG=d.
Указание: при рассмотрении равновесия ПЛ в поперечной плоскости в ее центре тяжести следует дополнительно приложить силу инерции, направленную вдоль радиуса циркуляции и вычисляемую как
, где m –масса ПЛ с учетом присоединенной массы воды в поперечном направлении (ее величину полагать известной).
Изобразим на рис. 11.6 плоскость, нормальную к траектории движения ПЛ (плоскость, проходящую через главную нормаль и бинормаль к траектории), ПЛ и силы, на нее действующие.
Поскольку при выполнении заданного маневра угол крена не изменяется, для изображенной системы сил можно записать систему уравнений равновесия:
Решив систему относительно угла крена , получим
- В силу конструктивных особенностей центр тяжести ПЛ располагается ниже точки приложения силы бокового давления, поэтому при циркуляции ПЛ наклоняется в сторону центра кривизны траектории движения.
- У надводных судов расположение центра тяжести может быть как ниже, так и выше точки приложения силы бокового давления. Очевидно, что в последнем случае судно будет наклонено в противоположную от центра кривизны сторону.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник: studopedia.ru
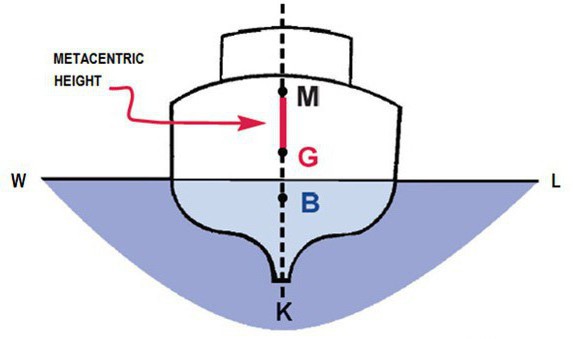
Метацентрическая высота — критерий остойчивости судна: формула
Определение метацентрической высоты можно сформулировать следующим образом. Что это? Это — расстояние между центром тяжести и метацентром корабля. Само по себе определение не очень понятное, а потому стоит добавить, что очень часто эту высоту выражают через остойчивость судна. Это происходит потому, что метацентр является основным критерием определения этой самой остойчивости.
Общие понятия
Как ранее было сказано, метацентрическая высота — это возвышение центра тяжести над метацентром самого корабля. Тут важно знать о том, что чем больше значение данной характеристики, тем большей будет изначальная остойчивость судна. Если же по каким-либо причинам эта высота отклоняется в сторону отрицательного значения, это говорит о том, что судно не сможет плавать без крена.
Что это значит? Допускать отрицательных значений метацентрической высоты ни в коем случае нельзя. Хотя. Получить точный ответ на вопрос о том, перевернется ли судно, имеющее отрицательное значение этой высоты, точно нельзя. Так как теория остойчивости распространяется лишь на наклонения кораблей, которые не превышают 10 градусов.
Правила и силы
Важно отметить, что существуют правила Классификационных Сообществ, которые следят за технической эксплуатацией судов. В данных документах описано, что эксплуатировать можно лишь те корабли, метацентрическая высота которых составляет не менее 0,2 метра. Чтобы понять, как будет вести себя тело с нулевой высотой, можно представить себе бочонок, плавающий в воде. Этот параметр данного тела будет равен 0, а его передвижение будет происходить вдоль продольной оси каждый раз, когда на него будет воздействовать любая внешняя сила, к примеру, волна или ветер.
Еще одна основа, которая позволяет кораблю плавать, — это сила тяжести. А также Архимедова сила. Естественно, сила тяжести будет тянуть корабль вниз, то есть на дно. Числовое значение этой характеристики равняется его весу, а прикладывается она к центру тяжести корабля. Архимедова сила, или, как ее еще называют, сила плавучести, выталкивает морское судно из воды.
Сила воздействия этого эффекта равняется водоизмещению корабля, которое приложено в центре подводного объема.
Работа сил
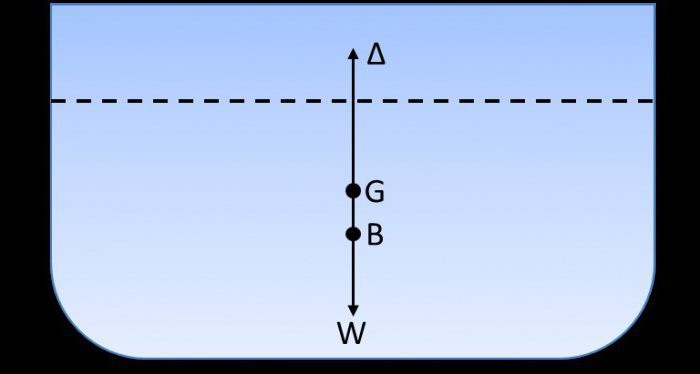
При «прямом» положении судна получается так, что эти две силы уравновешивают друг друга и находятся в одной вертикальной плоскости. Из-за этого корабль и способен перемещаться по воде. В том случае, если возникает крен судна, центр подводного объема ЦВ смещается в сторону наклона корабля. Смещение происходит из-за того, что меняется форма подводной части корпуса. Кроме того, при смещении ЦВ в одну из сторон возникает восстанавливающий момент, который будет противодействовать крену морского судна. При возникновении наклона ЦВ как бы начинает осуществлять поворот вокруг точки, которую условно называют метацентром m.

Расстояние от этой условной точки метоцентра m до центра тяжести судна ЦТ и будет являться его высотой. К примеру, для обычной гребной шлюпки числовое значение метацентрической высоты, которое будет являться достаточным для того, чтобы люди могли безопасно сесть и встать, равняется 0,3 м. В принципе, ничего сложного.
Как обеспечить остойчивость
Зная все то, что было описано выше, возникает явный вопрос о том, как же оценить безопасность лодки, парусной яхты, корабля и т. д.? Как понять, насколько велики шансы у корабля вернуться из положения «килем вверх» в нормальное, прямое состояние?
Для того чтобы добиться этого, необходимо улучшать остойчивость судна. Для этого существует несколько проверенных методов. Достаточно высокую остойчивость можно обеспечить за счет того, что на борту корабля будет размещен неподвижный балласт. Однако здесь нужно учитывать, что центр тяжести судна будет понижаться при дополнительной нагрузке. У кораблестроителей, моряков и всех, кто знаком с морским делом, есть такое правило: каждый килограмм груза, расположенный под ватерлинией, будет повышать остойчивость корабля, а вот каждый килограмм над этой линией будет ухудшать положение судна.
Восстановление судна
Для того чтобы увеличить вес, к примеру, яхты, ее оборудуют такой вещью, как неподвижный балластный киль. Но, здесь важно отметить, что он может быть размещен лишь на классическом типе яхты. Любой другой вид с таким килем окажется слишком тяжелым. Классические яхты — это абсолютная остойчивость речного судна, как ее называют.
Все дело в том, что эта категория кораблей может выпрямиться практически после любого крена. Угол крена, который необходим для того, чтобы судно не восстановилось, — 155 градусов. Это параметр такой яхты, как Contessa 32. Если говорить другими словами, речное судно этого класса сможет восстановиться в прямое положение даже после того, как опрокинется килем вверх.
Тут важно понимать, что крупные суда имеют большую остойчивость формы изначально из-за своих габаритов. Еще один важнейший момент — это то, что забортная вода не должна попасть вовнутрь корабля при крене через какие-либо люки или отверстия. Если это случится, жидкость, оказавшаяся на борту, способна свести на нет всю остойчивость.
Это произойдет из-за того, что вес попавшей воды сделает корабль тяжелее. Метацентрическая высота будет нарушена из-за смещения центра тяжести. И судно начнет тонуть.
Суда с надстройкой
Есть такой тип кораблей, которые обладают водонепроницаемой надстройкой. Естественно, вода не сможет попасть внутрь такого корабля, а это значит, что остойчивость останется на том же уровне даже при большом крене. Этот принцип стал основополагающим при изобретении спасательных шлюпок-неваляшек. Существуют спасательные плоты и шлюпки, которые считаются практически неопрокидываемыми из-за их конструкции. Такие категории кораблей способны восстановиться даже после того, как они полностью перевернулись.
Можно взять, к примеру, парусную яхту, которая обладает одним хитрым способом повышения остойчивости судна. Метод называется открениванием. А его суть заключается в том, что при наклоне будет перемещаться вес экипажа, балласта или качающегося киля по всей ширине судна. На сегодняшний день используется много различных типов перемещаемого балласта. А также существует один новейший, который заключается в наличии подводных управляемых крыльев.
Экспериментальная высота
Далее. Для того чтобы экспериментально вычислить метацентрическую высоту судна, можно перемещать большой груз по кораблю. Перемещение груза должно происходить на определенное расстояние Q от того места, где оно находилось изначально. Также при передвижении объекта нужно измерять малый угол вращения, который обозначается, как af. Числовое значение этой характеристики будет соответствовать углу наклона корабля.
Вот так будет выглядеть поперечная метацентрическая высота в формуле:
В — это ширина судна, которая должна измеряться в метрах, а Т — это период качки, определяющийся в секундах.
Именно такой способ вычислений, а также экспериментальный способ определения стали основными положениями, которые позволили принять высоту метацентра корабля за основной критерий его остойчивости.
Парусные суда
В настоящее время парусные суда являются одними из самых опасных в плане эксплуатации, а также самыми требовательными к остойчивости. Все дело в том, что при ветре парус такого судна будет постоянно подвергаться сильному воздействию воздуха, что в таких условиях будет являться основным моментом, создающим возможность для крена. Именно из-за наличия паруса суда с большими и длинными мачтами и, как следствие, большими парусами, нуждаются в наличии дополнительного тяжелого неподвижного балласта, который сильно снизит центр тяжести судна, создавая тем самым большее значение метацентрической высоты.
Очень важно отметить: довольно часто допускают такую ошибку, как оценка остойчивости корабля только по его метацентру. Конечно, эта высота будет являться основным критерием. Однако нельзя игнорировать те преимущества, которые имеются на всей диаграмме статической остойчивости. Туда входит не только высота метацентра.
Случаи неостойчивости
Существует три случая неостойчивости судна. Рассмотрим их подробнее.
Первый случай возникает в той ситуации, если высота h>0. Это возникает по причине того, что центр тяжести располагается выше, чем центр величины. При соблюдении этих условий и наклоне корабля в любую из сторон линия действия силы поддержания будет пересекать диаметральную плоскость выше, чем находится центр тяжести.
Второй случай неостойчивости произойдет тогда, когда метацентрическая высота будет равна нулю. В этом случае, практически, как и в предыдущем, центр тяжести окажется выше, чем центр величины. А при наклоне корабля случится так, что линия ЦТ будет проходить вдоль линии величины. В таком случае центр величины всегда будет расположен в одной вертикали с центром тяжести.
При таком расположении сил восстанавливающая пара, которая выравнивает корабль, будет просто отсутствовать. Без воздействия каких-либо внешних сил судно не сможет вернуться в свое исходное, прямое положение.
Источник: fb.ru