Лодки расстояние от корабля находится

Из всех задач на относительность движения мы будем в основном решать такие, которые связаны с законом сложения скоростей (1.30.7) или (1.30.8). Для этого удобно использовать понятия абсолютного, относительного и переносного движений.

Решая задачу, следует выбрать две системы координат и одну из них условно принять за неподвижную, после чего уяснить, какая скорость будет абсолютной, переносной и относительной. Далее надо записать закон сложения скоростей (1.30.8). После этого можно переходить к записи этого закона в проекциях на выбранные направления осей координат. Но можно воспользоваться и геометрическим сложением векторов.

Главные размерения

Главные размерения судна (основные размерения судна или корабля) — совокупность конструктивных, расчётных, наибольших и габаритных линейных размеров судна: длины, ширины, осадки и высоты борта. Главные размерения характеризуют мореходные качества корабля (судна) и определяют возможность его проводки в узкостях (каналах, бухтах, проливах), шлюзах, на мелководье, определяют возможность размещения на стапеле (слипе) или постановки в корабельный док.

№13. История одного корабля. 4 ЛОДКИ ГОРДОНА КЭМПБЕЛЛА.

Высота борта

Высота борта — вертикальное расстояние, измеряемое в плоскости мидель-шпангоута от основной плоскости до бортовой линии верхней палубы — линии пересечения теоретических поверхностей борта и верхней палубы или их продолжения при закруглённом соединении палубы с бортом. Для подводной лодки высота борта определяется как расстояние по вертикали между крайними точками наружного корпуса в районе мидель-шпангоута, но без учёта высоты ограждения рубки.

Осадка

Осадка — расстояние от горизонтальной плоскости, проходящей через нижнюю точку в середине длины корпуса (без учёта выступающих частей) до поверхности спокойной воды. Различают осадку носом, кормой и среднюю осадку, как среднеарифметическое значение кормовой и носовой осадки.

Длина

Длина судна — расстояние между его носовыми и кормовыми конструктивными элементами. Различают длину судна: по конструктивной ватерлинии, между перпендикулярами, наибольшую и габаритную. Для подводных лодок дополнительно различают: длину непроницаемого корпуса и длину прочного корпуса.

Длина корабля по конструктивной (расчётной) ватерлинии — расстояние между точками пересечения носовой и кормовой частей конструктивной ватерлинии с диаметральной плоскостью. Длина между перпендикулярами — расстояние между носовым и кормовым перпендикулярами корабля.

Наибольшая длина корабля — расстояние между крайними точками теоретической поверхности корпуса корабля в носовой и кормовой оконечностях. Габаритная длина судна — расстояние между крайними точками носовой и кормовой оконечностей корпуса с учётом выступающих частей. Длина непроницаемого корпуса подводной лодки — расстояние между концевыми поперечными переборками (чаще всего концевых цистерн главного балласта). Длина прочного корпуса — расстояние между крайними точками концевых переборок прочного корпуса.

Длина гражданского судна — расстояние, измеряемое на уровне летней грузовой ватерлинии от передней кромки форштевня до оси баллера руля или 96 % длины судна, измеряемой на уровне этой ватерлинии от передней кромки форштевня до крайней кромки кормовой оконечности судна.

Ширина

Ширина судна — расстояние между различными конструктивными точками корабля, расположенными на его правом и левом бортах. Различают наибольшую ширину, ширину по конструктивной ватерлинии, по расчётной ватерлинии, на мидель-шпангоуте, габаритную, ширину по стабилизаторам (для подводных лодок).

Наибольшей шириной корабля называют расстояние, измеряемое перпендикулярно диаметральной плоскости, между крайними точками теоретической поверхности корпуса корабля. Шириной корабля по конструктивной ватерлинии называют наибольшую ширину конструктивной ватерлинии. Шириной корабля по расчётной ватерлинии называют наибольшую ширину расчётной ватерлинии.

Шириной корабля на мидель-шпангоуте называют ширину конструктивной ватерлинии на мидель-шпангоуте. Габаритной шириной корабля называют расстояние, измеряемое перпендикулярно диаметральной плоскости между крайними точками корпуса корабля (судна), с учётом выступающих частей. Под шириной подводной лодки по стабилизаторам подразумевают размах стабилизаторов подводной лодки, то есть расстояние между крайними точками стабилизаторов.

• Деловой этикет
• ВАЗ-2107
• Филипп VI (король Франции)
• С чего начать строительство дома?
• Малый дворец Радзивиллов (Вильнюс)

Источник: gnezdoparanoika.ru

Относительность движения Примеры решения задач

1.Мимо пристани проходит плот. В этот момент в поселок, находящийся на расстоянииs1 = 15 км от пристани, вниз по реке отправляетсямоторная лодка. Она дошла до поселка за времяt= 3/4 ч и, повернув обратно, встретила плот на расстоянииs2 = 9 км от поселка. Каковы скорость течения рекиVи скорость лодки относительно водыv’?

Решение.Выберем систему отсчета, связанную с плотом (с водой). В этой системе отсчета плот покоится, а лодка движется вверх и вниз по реке с одинаковой по величине скоростью. Следовательно, время удаления лодки от плота равно времени приближения к нему. Поэтому время движения плота до встречи с лодкой равно 2tи его скорость (скорость течения) равна

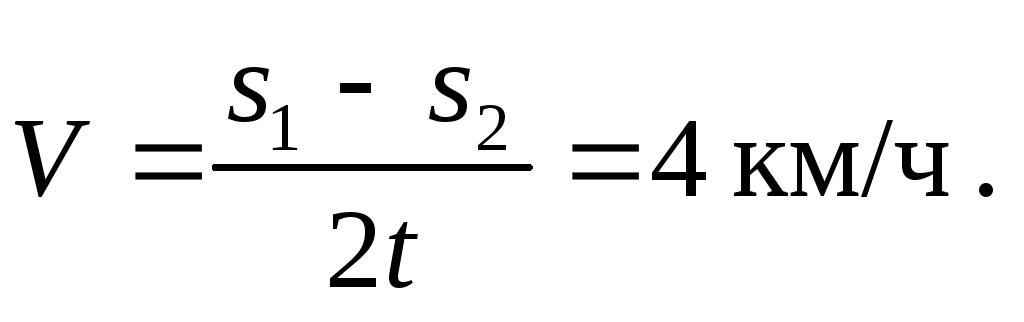
По закону сложения скоростей скорость лодки при ее движении вниз по реке относительно берега равна

С другой стороны

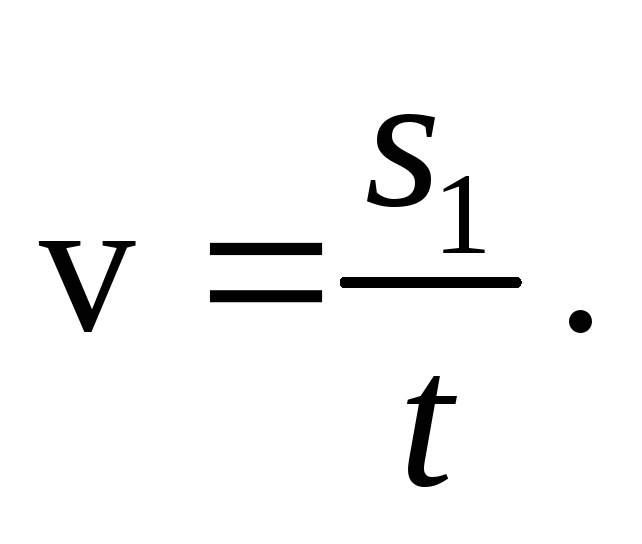
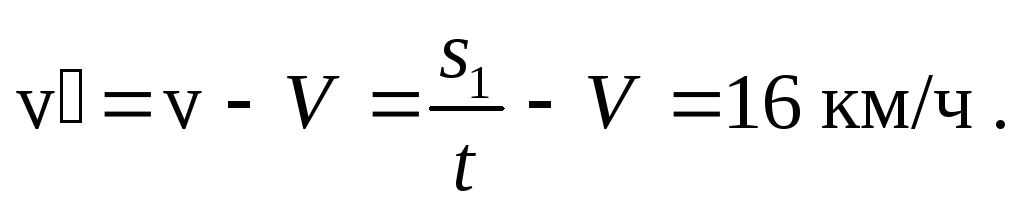
2.Скорость лодки в стоячей водеv’ меньше скорости течения рекиVвn= 2 раза. Под каким угломк берегу нужно держать корпус лодки во время переправы, чтобы снос лодки был минимальным?

Решение.Если лодку направить по течению реки, то, очевидно, снос будет бесконечно большим (лодка никогда не переправится на противоположный берег).

Такой же результат получается в случае, если направить лодку вверх по течению реки. Значит, существует некоторое направление, при котором снос лодки минимален. Если — скорость лодки в стоячей воде, а— скорость течения реки, то скорость лодки относительно берега определится законом сложения скоростей:

.

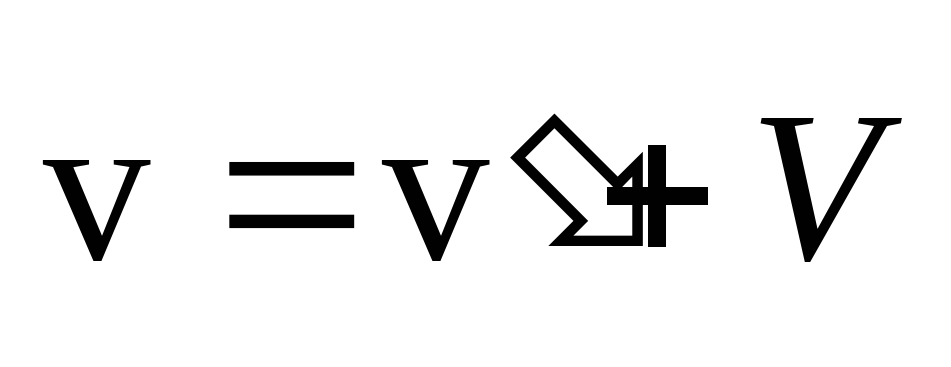
Векторное сложение скоростей, соответствующее этому закону, показано на рисунке. Там же показаны система отсчета x0y, связанная с берегом, и угол, определяющий направление вектора. Очевидно, что величина сноса лодки равна

s = vх  t,

где vx = V – vcos — проекция скорости на осьx, — время переправы. Здесьd — ширина реки, vy — проекция скорости на осьy.

Запишем выражение для величины сноса в явном виде:

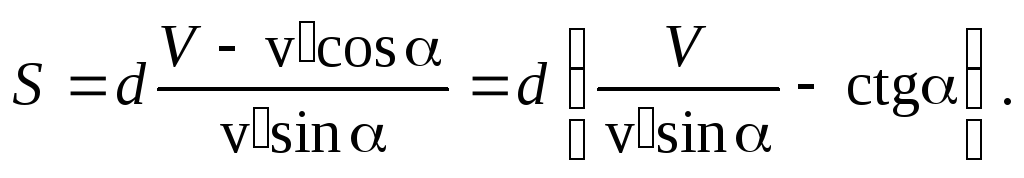
Минимум сноса соответствует минимуму выражения в скобках. Найдем угол , при котором достигается этот минимум из условия, что производная поот этого выражения должна равняться нулю в точке минимума. Дифференцирование дает:

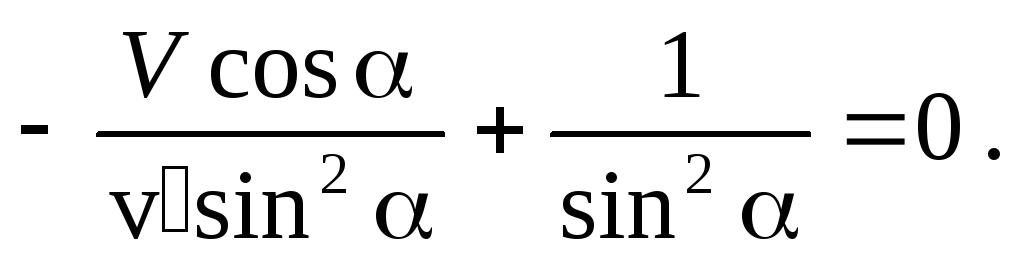
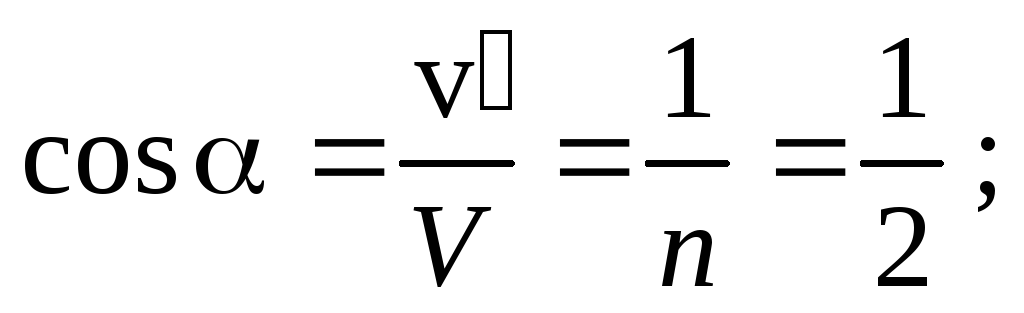
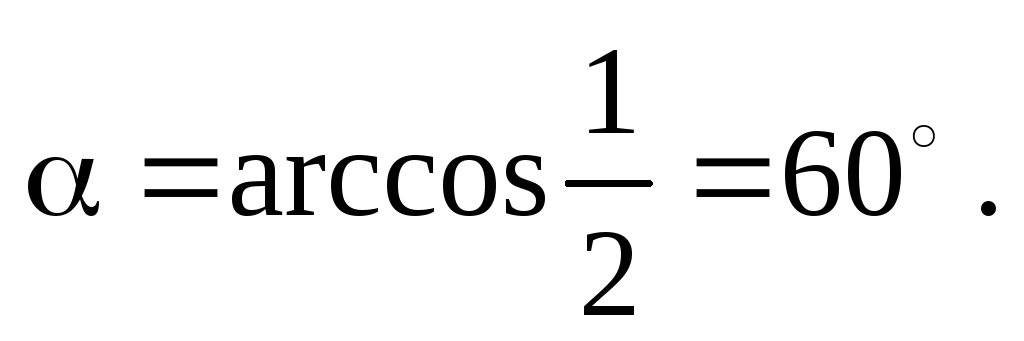
3. Приборы, установленные на корабле, идущем на север со скоростью V = 10 м/с, показывают скорость ветра v’ = 5 м/с, а его направление — восточное. Что покажут аналогичные приборы, установленные на берегу?

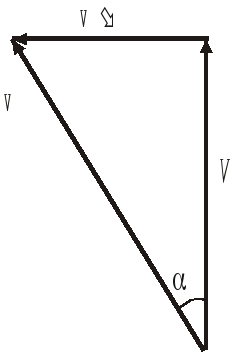
Решение.По закону сложения скоростей скорость ветра относительно берега равна

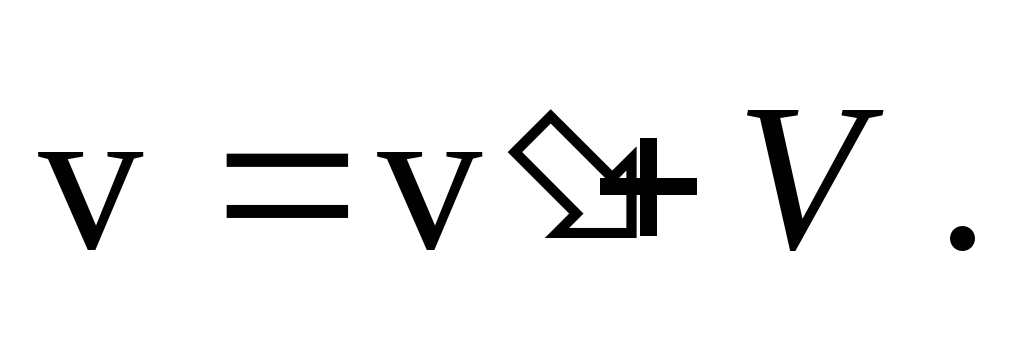
Найдем эту скорость построением (см. рис.). Из рисунка следует:

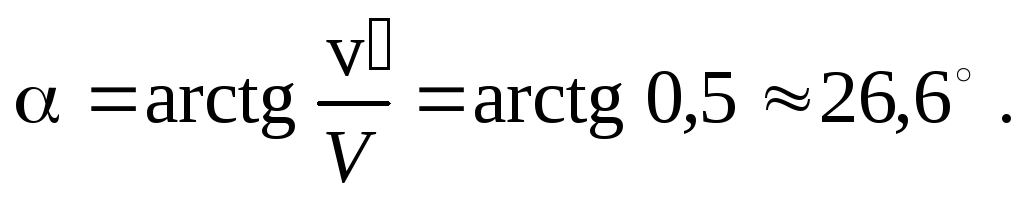
4.Два корабля движутся перпендикулярными курсами с постоянными скоростямиv1= 15 км/ч иv2= 20 км/ч. В некоторый момент времени они находятся на расстоянииS = 10 км друг от друга, а вектор скорости первого корабля составляет с линией, соединяющие корабли, угол= 30. На какое минимальное расстояниеdкорабли сблизятся при своем движении?

ешение.Положение кораблей в момент времени, соответствующий условию задачи, показано на верхнем рисунке. Рассмотрим движение кораблей в системе отсчета, связанной с первым кораблем (см. нижний рис.). В этой системе первый корабль покоится, а второй движется прямолинейно со скоростью, определяемой из закона сложения скоростей:

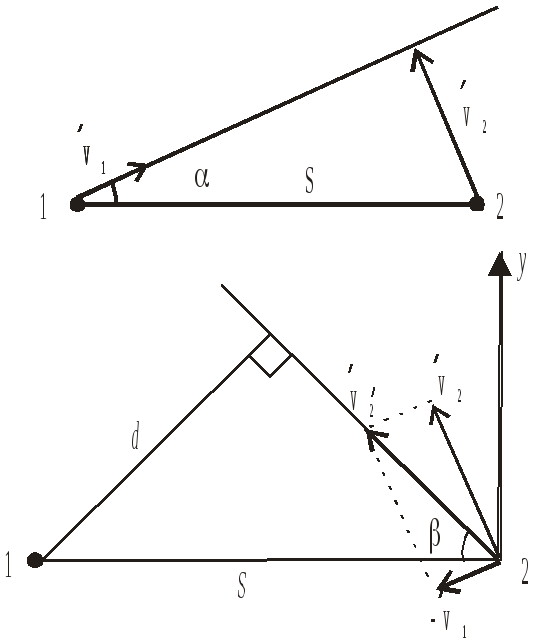
скомое расстояниеd- это расстояние от первого корабля до прямой линии, по которой движется второй корабль в системе отсчета, в которой первый корабль покоится. Из рисунка и элементарных геометрических соображений находим:

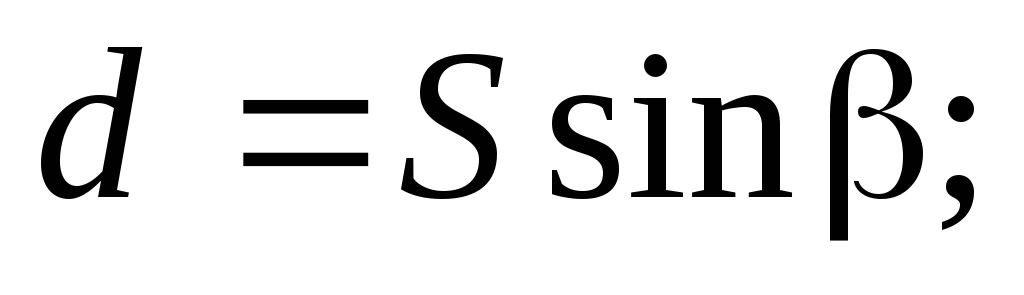
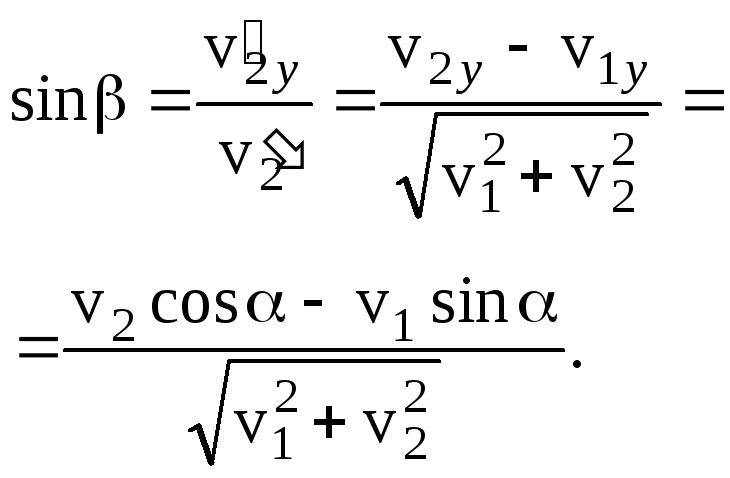
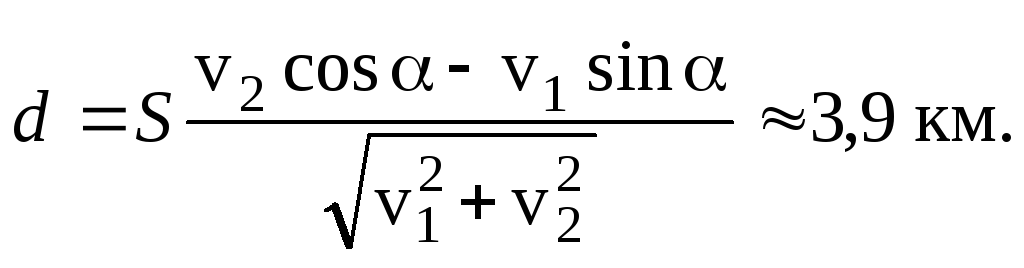
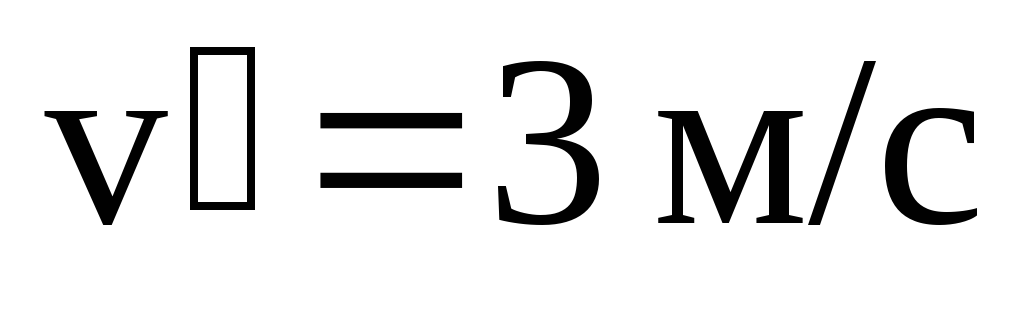
5.Скорость лодки в стоячей воде, скорость течения рекиv= 4 м/с, а ширина рекиL= 360 м. Под каким угломк берегу нужно держать нос лодки, чтобы переправиться на противоположный берег в кратчайшее время? Чему равно это времяTmin? Какой путьSпроплывет за это время лодка?

Решение.По закону сложения скоростей скорость лодкиотносительно берега равна

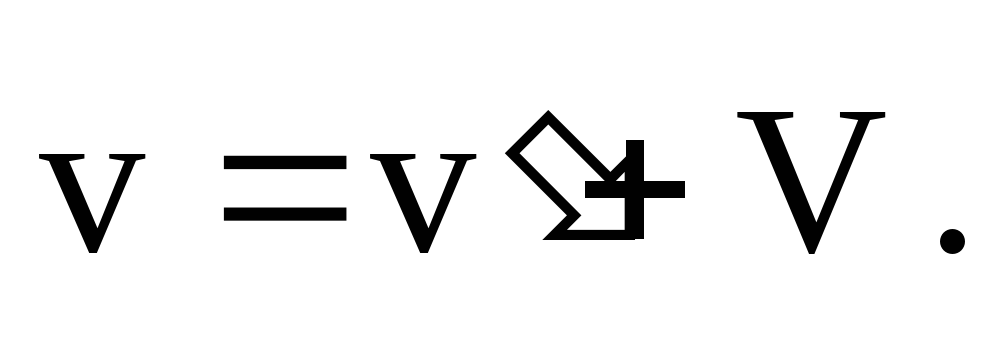
Движение лодки можно рассматривать как наложение двух движений, одно из которых происходит перпендикулярно берегу, а другое — по течению реки. Первое происходит со скоростью 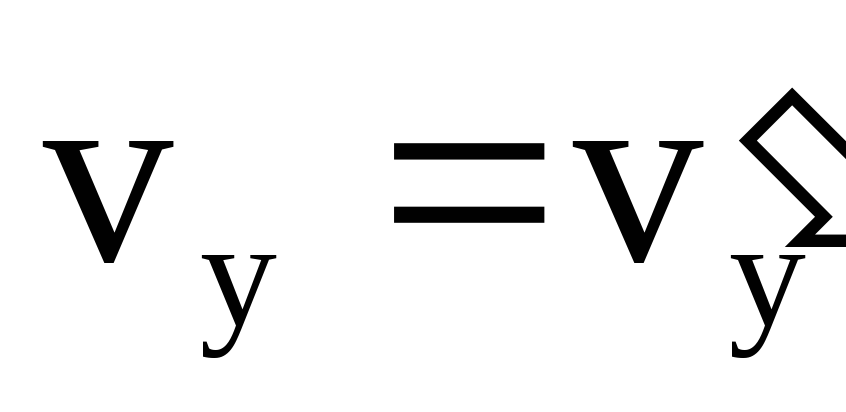, а второе — со скоростью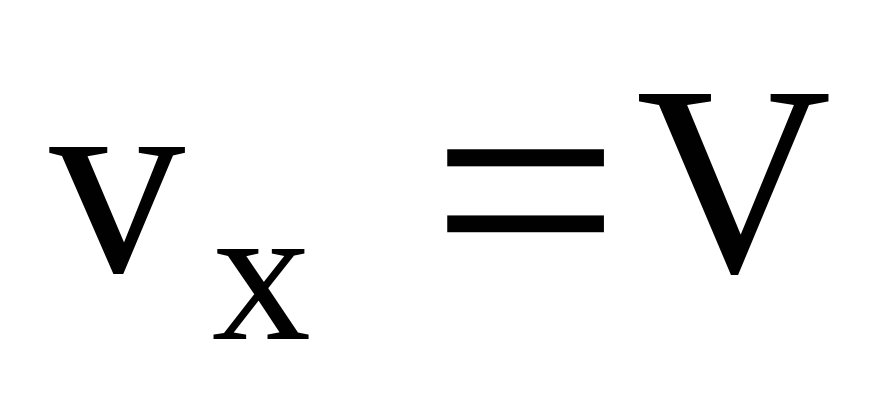. Тогда времяT переправы на противоположный берег

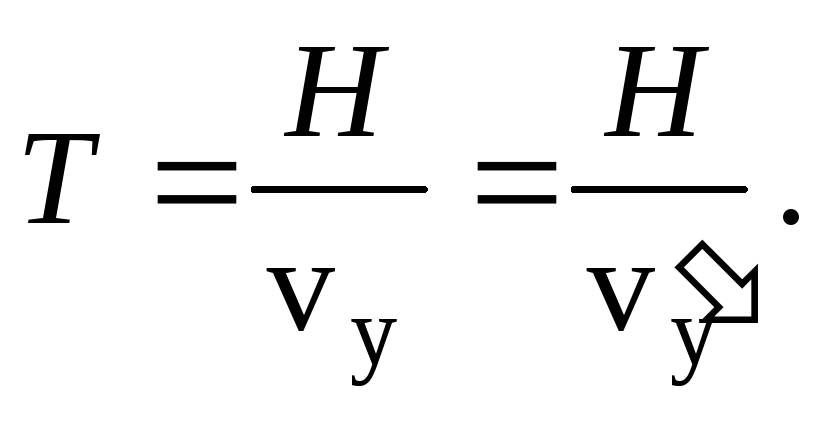
Это время будет минимально в том случае, когда проекция скорости на ось y, перпендикулярную к берегу, максимальна, т.е. равна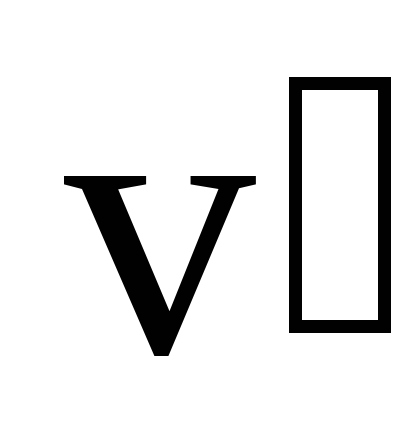. В этом случае скорость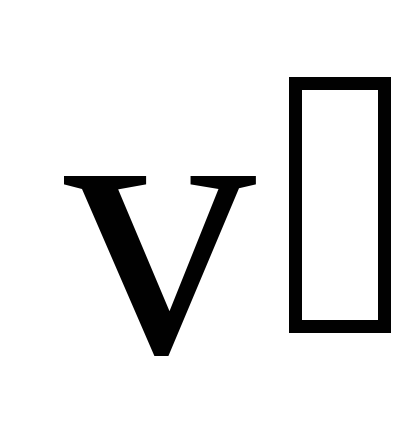перпендикулярна берегу, т.е.= 90, а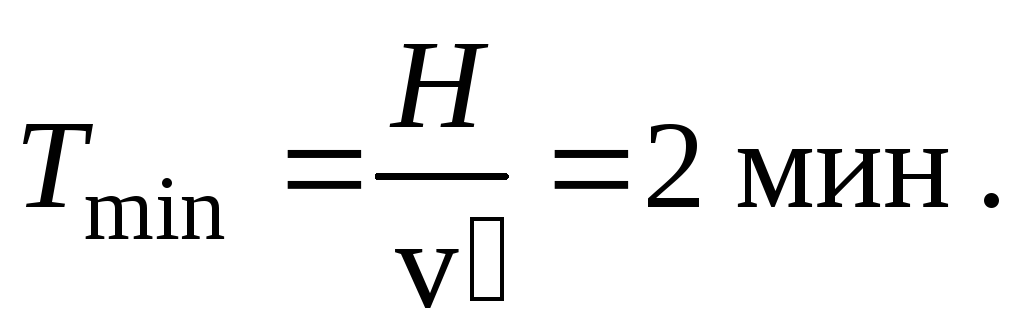

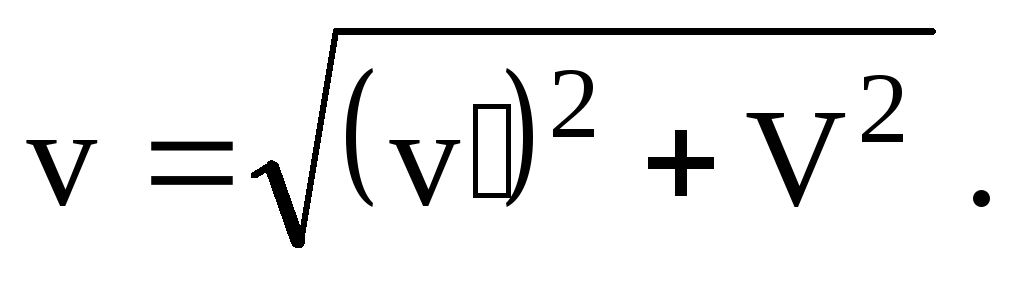
Скорость лодки относительно берега Следовательно, за времяTminлодка пройдет путь

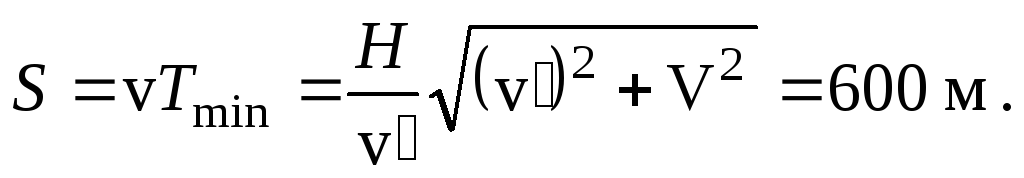
6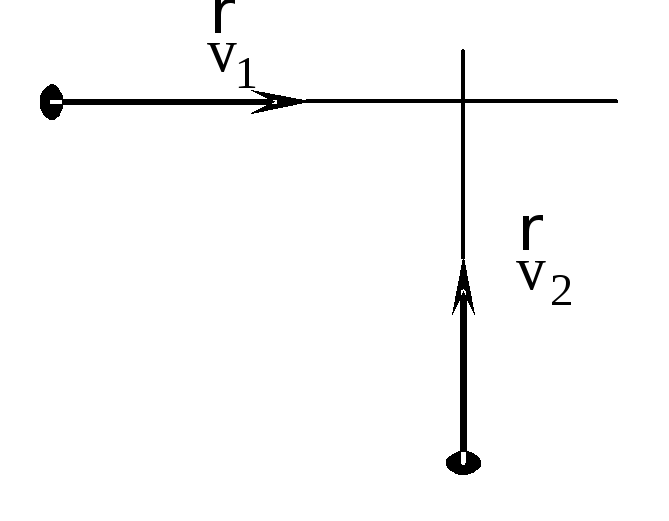.Два пешехода движутся к перекрёстку по дорогам, пересекающимися под прямым углом. Найти их относительную скорость, если скорость первого пешехода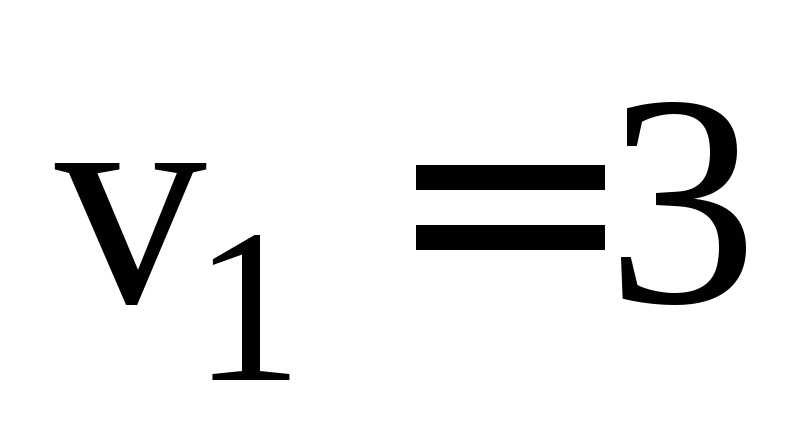км/ч, а скорость второго —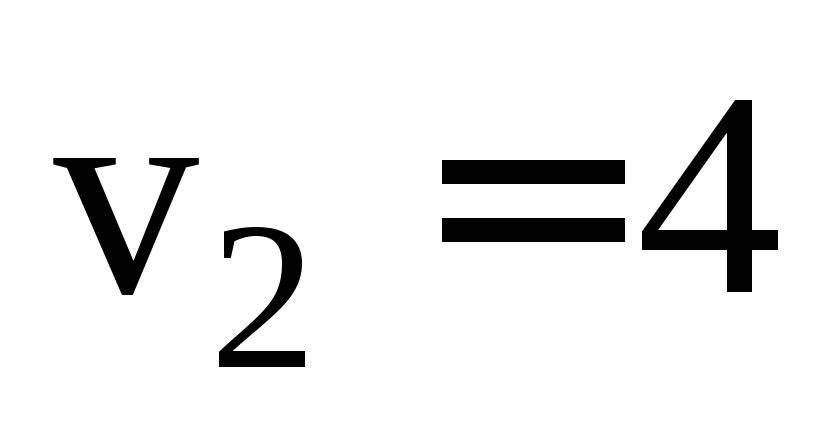км/ч.

Решение.Изобразим на рисунке скорости пешеходов. По определению скорость первого пешехода относительно второго равна:

.

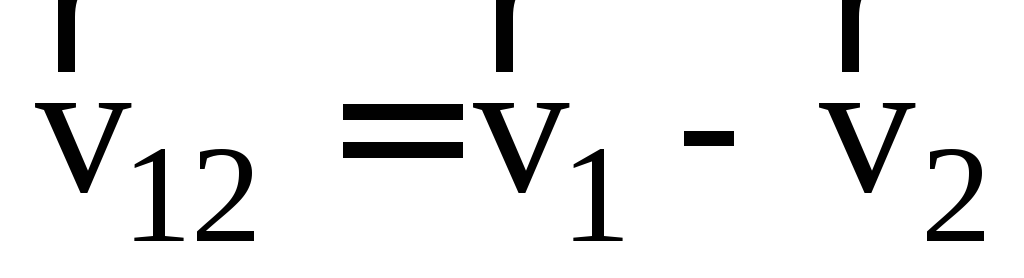
Найдем построением эту скорость (см. рис.).

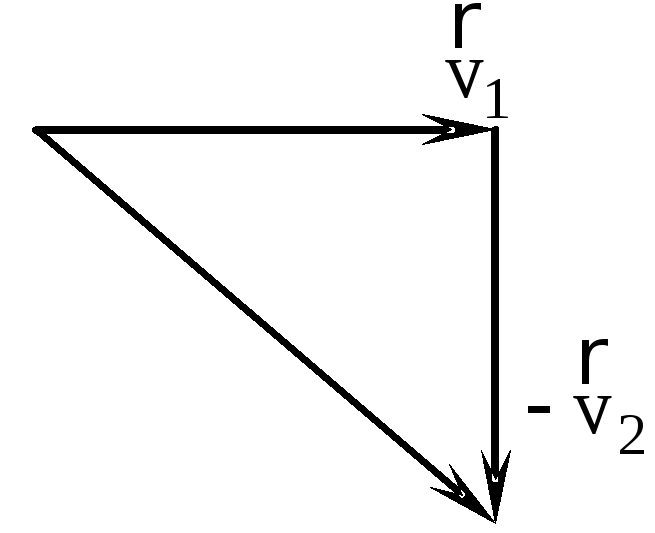
Из рисунка видно, что

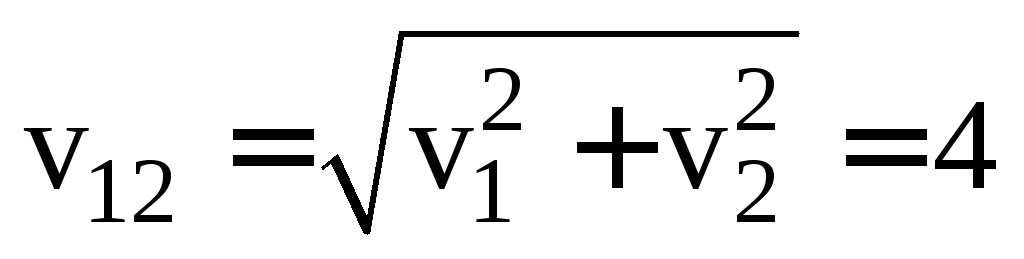
км/ч.

Источник: studfile.net