Презентация 8 класса по предмету «Физика и Астрономия» на тему: «Выполнена : учителями физики МОУ « Лицей 15» Ларионовым В. С, Ларионовой Н. В. ученицей 8 класса « А » МОУ « Лицей 15» Гуровой Т. А. Уровень жидкости в.». Скачать бесплатно и без регистрации. — Транскрипт:
1 Выполнена : учителями физики МОУ « Лицей 15» Ларионовым В. С, Ларионовой Н. В. ученицей 8 класса « А » МОУ « Лицей 15» Гуровой Т. А. Уровень жидкости в сосудах Саров 2010 МОУ «Лицей 15»
2 ЗАДАЧА В цилиндрическом сосуде с водой плавает кусок льда. Изменится ли уровень воды в сосуде, если лёд растает? ?
3 ЦЕЛЬ УРОКА Изучить 2 способа решения задач об изменении уровня жидкости в сосуде. Сформулировать алгоритмы решения. ЦЕЛЬ УРОКА
4 2 СПОСОБА РЕШЕНИЯ ЗАДАЧИ через объёмычерез давление на дно
5 1.Запишем условие плавания для кусочка льда: Fа = Fт. Fа = Fт. 2.Воспользуемся законом Архимеда: ρ ж gV в.ж = m л g, где m л – масса льда, V в.ж – объём вытесненной жидкости. 3. Откуда V в.ж = m л /ρ ж. 4. После таяния льда объём воды в сосуде увеличился на ΔV= m л /ρ ж. (Очевидно, что масса талой воды равна массе льда.) 5. Откуда следует, что V в.ж. = ΔV, т.е. h 1 = h 2. РЕШЕНИЕ
10 КГ САМОДЕЛЬНОЙ БОМБОЧКИ В ОГРОМНЫЙ БАССЕЙН..#янгер #shorts
6 ОТВЕТ : Уровень воды в сосуде не изменится.
7 1. Записать условие плавания тела : F т =F а. (1) 2. Воспользоваться законом Архимеда : F а = ρ ж gV в. ж. (2) 3. Используя уравнения (1) и (2) и расписав F т выразить объём вытеснённой жидкости V в. ж. 4. Рассчитать на сколько измениться уровень воды в сосуде по сравнению с изначальным ( до погружения тела в воду ) после таяния льда ( или других действий ): Δ V. 5. Сравнить V в. ж. с Δ V и сформулировать ответ. АЛГОРИТМ решения задачи через объёмы
8 2 СПОСОБА РЕШЕНИЯ ЗАДАЧИ через объёмычерез давление на дно 1. F т =F а 2. F а = ρ ж gV в. ж 3. V в. ж. 4. Δ V. 5. V в. ж. ? Δ V
9 h1h1 h2h2 1.С одной стороны, силу давления на дно в 1-ом и во 2-ом случаях можно выразить следующим образом F д1 = (m л +М)g, F д2 = (m в +М)g, где m л – масса льда, M – первоначальная масса воды в стакане без льда, m в – масса воды, образовавшейся после таяния льда. Т.к. m л = m в, то F д1 = F д2. 2. С другой стороны: F д1 = p 1 S = gh 1 S, F д2 = p 2 S = gh 2 S. 3. Т.к. F д1 = F д2, то h 1 = h 2. РЕШЕНИЕ
10 ОТВЕТ : Уровень воды в сосуде не изменится.
11 1. Содержимое сосуда не изменилось, поэтому не изменилась и сила давления на дно сосуда : F д 1 =F д 2. (1) 2. Выразить F д 1 и F д 2, воспользовавшись определительной формулой давления p= F д /S и формулой гидростатического давления p= ρ gh: F д 1 = …, F д 2 =… (2) 3. Из уравнений (1) и (2) выразить высоты h 1 и h 2 и сравнить. АЛГОРИТМ решения задачи через давление на дно сосуда 12 2 СПОСОБА РЕШЕНИЯ ЗАДАЧИ через объёмычерез давление на дно 1. F т =F а 2. F а = ρ ж gV в. ж 3. V в. ж. 4. Δ V. 5. V в. ж. ? Δ V 1. F д 1 =F д p= F д /S F д 1 = … p= ρ gh F д 2 =… 3. (1) и (2) h 1 ? h 2
13 Задача « Пузырёк воздуха во льду » Задача « Пузырёк воздуха во льду » Задача « Вмёрзшая сталь » Задача « Вмёрзшая сталь » Задача « Кастрюля » Задача « Кастрюля » Задача « Непотопляемая лодка » Задача « Непотопляемая лодка » Задача « Лишнее за борт » Задача « Лишнее за борт » КЛЮЧЕВЫЕ ЗАДАЧИ Подведение итогов урока
Первый раз с 10 метров | Скала в Blue Tree Phuket Таиланд #клиффдайвинг #бассейн #аквапарк
14 Пузырёк воздуха во льду Условие Решение Ответ
15 Условие В сосуде с водой плавает кусок льда, в котором находится пузырёк воздуха. Через некоторое время лёд растаял. Изменился ли уровень воды в сосуде ? ? См. алгоритмы
16 через объёмычерез давление на дно 1. F т =F а 2. F а = ρ ж gV в. ж 3. V в. ж. 4. Δ V. 5. V в. ж. ? Δ V 1. F д 1 =F д p= F д /S F д 1 = … p= ρ gh F д 2 =… 3. (1) и (2) h 1 ? h 2 В сосуде с водой плавает кусок льда, в котором находится пузырёк воздуха. Через некоторое время лёд растаял. Изменился ли уровень воды в сосуде ? Алгоритмы Вернуться назад
17 Решение 1. С одной стороны, силу давления на дно в 1-ом и во 2-ом случаях можно выразить следующим образом: F д1 = (m л +М)g, F д2 = (m в +М)g, где m л – масса льда, M – масса воды в первоначальном стакане без льда, m в – масса воды, образовавшейся после таяния льда (т.к. m воз
18 Уровень воды в сосуде не изменится. Ответ
19 Вмёрзшая сталь Условие Решение Ответ
20 Условие В сосуде с водой плавает кусок льда с вмёрзшим в него стальным шариком. Через некоторое время лёд растаял. Изменился ли уровень воды в сосуде ? ? См. алгоритмы
21 через объёмычерез давление на дно 1. F т =F а 2. F а = ρ ж gV в. ж 3. V в. ж. 4. Δ V. 5. V в. ж. ? Δ V 1. F д 1 =F д p= F д /S F д 1 = … p= ρ gh F д 2 =… 3. (1) и (2) h 1 ? h 2 Алгоритмы Вернуться назад В сосуде с водой плавает кусок льда с вмёрзшим в него стальным шариком. Через некоторое время лёд растаял. Изменился ли уровень воды в сосуде ?
22 Решение hh1h1 1.Т.к. содержимое сосуда не изменилось, то F д1 = F д2. 2.C другой стороны : F д1 = gh 1 S, F д2 = gh 2 S+ P, где Р – вес шарика в воде, S – площадь дна сосуда, – плотность воды. 3. Т.к. F д1 = F д2, то gh 1 S = gh 2 S + P Откуда следует, что h 1 > h 2.
23 Уровень воды в сосуде понизится. Ответ
24 Кастрюля Условие Решение Ответ
25 Условие В большом сосуде на поверхности воды плавает стальная кастрюля. Кастрюлю утопили. Изменился ли уровень воды в сосуде ? ? См. алгоритмы
26 через объёмычерез давление на дно 1. F т =F а 2. F а = ρ ж gV в. ж 3. V в. ж. 4. Δ V. 5. V в. ж. ? Δ V 1. F д 1 =F д p= F д /S F д 1 = … p= ρ gh F д 2 =… 3. (1) и (2) h 1 ? h 2 Алгоритмы Вернуться назад В большом сосуде на поверхности воды плавает стальная кастрюля. Кастрюлю утопили. Изменился ли уровень воды в сосуде ?
27 Решение h 1 +h 0 h 2 +h 0 S h 0 – уровень воды в сосуде с водой. 1. Запишем условие равновесия для плавающей кастрюли и воспользуемся законом Архимеда: F а = V 1 g = m к g. 2. Выразим объёмы вытесненной воды в 1-ом и 2-ом случаях: V 1 = mк : в, V 2 = m к : к. Т.к. в V 2 h 2 28 Уровень воды в сосуде понизится. Ответ
29 Непотопляемая лодка Условие Решение Ответ
30 Условие В небольшом бассейне плавает полузатопленная лодка, причём уровень воды в ней совпадает с уровнем в бассейне. Из лодки зачерпнули ведро воды и вылили за борт. Как изменился уровень воды в бассейне ? ? См. алгоритмы
31 через объёмычерез давление на дно 1. F т =F а 2. F а = ρ ж gV в. ж 3. V в. ж. 4. Δ V. 5. V в. ж. ? Δ V 1. F д 1 =F д p= F д /S F д 1 = … p= ρ gh F д 2 =… 3. (1) и (2) h 1 ? h 2 Алгоритмы Вернуться назад В небольшом бассейне плавает полузатопленная лодка, причём уровень воды в ней совпадает с уровнем в бассейне. Из лодки зачерпнули ведро воды и вылили за борт. Как изменился уровень воды в бассейне ?
32 Решение V1V1 V2V2 S S 1. Из условия равновесия лодки и закона Архимеда получим: V 1 = М : V 2 = (М – m) : где М – масса лодки с водой, m – масса воды в ведре, – плотность воды. 2. Изменение объёмов содержимого бассейна по сравнению с первоначальным объёмом воды V 1 = V 1 = M: в, V 2 = V 2 + V в.в = (M – m) : в + m в : в = М : в ( где V в.в – объём ведра воды). Откуда следует, что V 1 = V Т.к. V 1 = Sh 1, V 2 = Sh 2, (где S – площадь дна бассейна, h 1 и h 2 – изменения уровня воды по сравнению с первоначальным уровнем), то h 1 = h 2. h1h1 h2h2
33 Ответ Уровень воды в бассейне не изменился.
34 Лишнее за борт Условие Решение Ответ
35 Условие В небольшом бассейне плавает лодка. Лежащий на дне лодки камень бросили в воду. Как изменился уровень воды в бассейне ? ? См. алгоритмы
36 через объёмычерез давление на дно 1. F т =F а 2. F а = ρ ж gV в. ж 3. V в. ж. 4. Δ V. 5. V в. ж. ? Δ V 1. F д 1 =F д p= F д /S F д 1 = … p= ρ gh F д 2 =… 3. (1) и (2) h 1 ? h 2 Алгоритмы Вернуться назад В небольшом бассейне плавает лодка. Лежащий на дне лодки камень бросили в воду. Как изменился уровень воды в бассейне ?
37 Решение h 1 +h 0 h2+h0h2+h0 h 0 – изначальный уровень воды в бассейне 1. Из условия равновесия для лодки запишем объёмы вытесненной воды в двух случаях: V 1 = m к : в + m л : в, V 2 = m л : в + m к : к, где m л – масса лодки, m к – масса камня, в – плотность воды, к – плотность камня. 2.Т.к. в V 2 h 1 > h 2 h 1 +h 0 > h 2 +h 0.
38 Ответ Уровень воды в бассейне понизился.
39 через объёмычерез давление на дно 1. F т =F а 2. F а = ρ ж gV в. ж 3. V в. ж. 4. Δ V. 5. V в. ж. ? Δ V 1. F д 1 =F д p= F д /S F д 1 = … p= ρ gh F д 2 =… 3. (1) и (2) h 1 ? h 2 Алгоритмы Вернуться назад Изучить 2 способа решения задач об изменении уровня жидкости в сосуде. Сформулировать алгоритмы решения. ЗАДАЧИ УРОКА Библиография
40 Библиография 1. Гельгафт И.М., Генденштейн Л.Э., Кирик Л.А задача по физике с решениями. Учебное пособие. – Харьков-Москва, – 592 с. 2. Городские олимпиады по физике г. Нижнего Новгорода гг. Сборник задач. – Н.Новгород: Институт прикладной физики РАН, –52с. 3. Подлесный Д.В. Анализ давления на дно сосуда в задачах гидростатики. // Потенциал, 10, – С Полянский С.Е.
Поурочные разработки по физике. – М.: ВАКО, –240с. 5. Черноуцан А. Гидростатика в стакане. // Квант, 3, – С Чивилёв В.И. Олимпиада «Физтех-2005». // Потенциал, 5, – С.59-61
Источник: www.myshared.ru
Лодка плавает в небольшом бассейне камень
Давление твердых тел, жидкостей и газов.
54. Брусок массой 2 кг имеет форму параллелепипеда. Лежа на одной из граней, он оказывает давление 1 кПа, лежа на другой – давление 2 кПа, стоя на третьей – давление 4 кПа. Каковы размеры бруска?
55. В мензурке находятся 3 слоя жидкостей (ртуть, вода и машинное масло) толщиной по 20 см . На какой глубине давление в жидкости равно 7,9 кПа? Атмосферное давление не учитывайте.
56. В каком сосуде раньше появятся пузырьки воздуха, если дуть в трубку с двумя ответвлениями? Какое избыточное давление p в трубке нужно создать для выдувания первых пузырьков, если высота керосина h B 1 B = 30 см , а высоты воды h B 2 B = 20 см ?
57. Какая жидкость раньше попадет в верхнюю часть трубки, если не дуть в нее, а втягивать воздух?
58. Из мелкокалиберной винтовки поочередно стреляют в два стакана. В первом образуются отверстия, а второй разлетается вдребезги. Попробуйте объяснить это явление.
59. Сила давления воды на дно прямоугольного аквариума равна 60 Н. На меньшую из боковых стенок, ширина которой 20 см , вода давит с силой 10 Н. Какова сила давления воды на большую из боковых стенок? Атмосферное давление не учитывайте.
60. На горизонтальном листе резины лежит перевернутая кастрюля радиусом R = 10 см и высотой H = 15 см . В дне кастрюли просверлено круглое отверстие радиуса r = 1 см , в которое плотно вставлена легкая вертикальная трубка. В кастрюлю через трубку наливают воду. Когда вода заполняет всю кастрюлю и поднимается по трубке на h = 4 см , она начинает вытекать из-под краев кастрюли. Какова масса m кастрюли?
61. На горизонтальном листе резины лежит перевернутый котелок, имеющий форму полусферы радиусом R . В верхней точке перевернутого котелка имеется маленькое отверстие, через которое наливают воду. При какой массе котелка вода может вытекать снизу?
62. Два тяжелых вертикальных поршня жестко связаны между собой стержнем длиной l . Площадь меньшего нижнего поршня S , площадь большего 2 S . Найдите давление жидкости на больший поршень, если общая масса поршней и стержня M , а плотность жидкости r . Атмосферное давление не учитывайте.
63. Уровень воды в U -образной трубке на h = 45 см ниже краев трубки, В одно из колен трубки понемногу доливают керосин. При какой высоте столба керосина жидкость начинает переливаться через край трубки? Какая это будет жидкость?
64. В U -образной трубке находятся ртуть, вода и керосин. Найдите высоту столбов воды и керосина, если в правом колене трубки уровень ртути на h = 1 см выше, чем в левом.
65. Пять одинаковых сообщающихся сосудов частично заполнены водой. В один из сосудов доливают слой керосина высотой h = 25 см . На сколько поднимется уровень воды в остальных сосудах?
66. В цилиндрических сообщающихся сосудах, площади сечения которых относятся как 3:1, находится вода, В узкий сосуд доливают слой керосина высотой 25 см . На сколько поднимется уровень воды в широком сосуде? Керосин в этот сосуд не попадает.
67. На шкале барометра иногда делают надписи «Ясно» или «Облачно». Какая из этих надписей соответствует более высокому давлению? Почему предсказания барометра не всегда оправдываются? Что будет предсказывать барометр на вершине высокой горы?
68, Раньше на самолетах устанавливали барометры-анероиды, чтобы по их показаниям летчик мог судить о высоте полета (ведь атмосферное давление изменяется с высотой). Почему этот метод оказался не очень надежным, особенно при полетах на малых высотах?
69. Из воды вынимают вверх дном легкую кружку. Какую силу F необходимо прикладывать в тот момент, когда дно кружки находится на высоте h = 10см над поверхностью воды, если площадь дна S = 100 см P 2 P ?
70. Трубку ртутного барометра подвесили к динамометру. Как будет изменяться показание динамометра при изменении атмосферного давления?
71. Оцените массу атмосферы Земли, воспользовавшись табличными сведениями.
72. Каким (примерно) стало бы давление атмосферы, если бы все океаны испарились? Воспользуйтесь табличными сведениями.
73. Какую силу F нужно приложить, чтобы оторвать друг от друга магдебургские полушария? Радиус полушарий r = 10 см . Давлением воздуха внутри полушарий можно пренебречь.
74. Будет ли изменяться вследствие изменений атмосферного давления объем пузырька воздуха, случайно попавшего в барометрическую трубку и «разорвавшего» столбик ртути? Изменится ли ответ, если трубку наклонить так, чтобы ртуть заполнила ее доверху?
75. Сифон. Изогнутая трубка, заполнена жидкостью. Концы трубки закрыты. Что произойдет, если их открыть? Если открыть только один конец?
76. Изогнутая трубка заполнена водой и закрыта с одного конца. Что произойдет, если открыть трубку?
77. Почему ни один из астероидов (малых планет) не имеет атмосферы?
Архимедова сила. Плавание тел.
78. Какова плотность подвешенного к динамометру бруска, если при полном погружении бруска в керосин показание динамометра уменьшается с 12 Н до 8 Н?
79. Когда подвешенный к динамометру полый алюминиевый цилиндр опустили в керосин, показание динамометра уменьшилось в 1,5 раза. Какую часть объема цилиндра занимает полость?
80. Аристотель взвешивал пустой кожаный мешок и тот же мешок, заполненный воздухом. В обоих случаях показания весов оказались одинаковыми. Аристотель сделал из этого вывод, что воздух ничего не весит, В чем состояла его ошибка? ‘
81. Мост опирается на вертикальные сваи, которые глубоко уходят в твердый грунт дна реки. Действует ли на сваи архимедова сила?
82. Брусок находится на границе двух жидкостей, имеющих плотности r B 1 B , и r B 2 B , вытесняя объемы V B 1 B , и V B 2 B соответствующих жидкостей. Какая архимедова сила действует на брусок?
83. Взвешивание на рычажных весах производят с помощью стальных гирь. При взвешивании каких тел архимедова сила со стороны воздуха совершенно не снижает точности взвешивания?
84. Камень лежит на дне сосуда с водой: а) полностью погруженным в воду; б) наполовину погруженным в воду. Как изменится сила давления камня на дно в случаях а) и б), если сверху долить керосин (керосин не смешивается с водой)?
85. В стоящий на весах сосуд с водой опускают на нити чугунный брусок массой 700 г , который полностью погружается в воду, но не касается дна или стенок сосуда. На сколько изменятся показания весов? Вода из сосуда не выливается.
86. Ведро с водой стоит на весах. Как изменятся показания весов, если в воду опустить на легкой веревке чугунный шар массой 7 кг ? Рассмотрите два случая: а) конец веревки держат в руках; б) конец веревки привязан к дужке ведра.
87. Лодка плавает в маленьком бассейне. Как изменится уровень воды в бассейне, если выбросить из лодки в бассейн камень?
88. В стакане с водой плавает кусок льда. Как изменится уровень воды в стакане, когда весь лед растает. Как изменится уровень воды в стакане, если в кусок льда была вморожена: а) пробка; б) свинцовый шарик?
89. Полузатопленная лодка плавает в маленьком бассейне. Как изменится уровень воды в бассейне, если вычерпать воду из лодки в бассейн?
90. В аквариуме с вертикальными стенками высота слоя воды 10 c м. Когда мальчик спустил на воду металлическую лодочку, уровень воды стал 13 см , а когда он перевернул и утопил эту лодочку, уровень воды опустился до 11 см . Какова плотность r сплава, из которого сделана лодочка?
91. В закрытой пластиковой бутылке плавает открытая перевернутая пробирка «водолаз», утяжеленная снизу пластилином. Если стенки бутылки сжать рукой, пробирка тонет. Объясните поведение «водолаза».
92. Маленькая льдинка плавает в широком сосуде с водой. Поднимется или опустится льдинка, если сверху долить керосин?
93. Льдинка плавает на границе между водой и керосином. Какая часть ее объема находится ниже границы раздела жидкостей, если керосин покрывает льдинку полностью?
94. Сигнальный буй объемом 0,6 м P 3 P плавает в заливе. Во время прилива якорная цепь натянута и буй погружен в воду наполовину. Во время отлива цепь не натянута и буй погружен в воду на 20 % своего объема. Удастся ли во время отлива поднять якорь вертикальной силой 1,5 кН?
95. Как измерить плотность пластилина, используя только мензурку с водой?
96. В вашем распоряжении широкая мензурка, кусок пластилина и металлический шарик. Как измерить плотности пластилина и металла? Проделайте этот опыт.
97. На дне аквариума стоит склеенная из 4 одинаковых кубиков деталь. Длина ребра каждого кубика 10 см . В аквариум медленно наливают воду. Когда высота уровня воды достигает 10 см , деталь отрывается от дна. Опыт повторяют, натерев нижнюю грань детали парафином (теперь вода не подтекает под эту грань). До какой высоты h нужно теперь налить в аквариум воду, чтобы деталь оторвалась от дна?
Работа. Мощность. Энергия. Простые механизмы.
98. Пружина растянута на 10 см . Ее удерживают в растянутом состоянии, прикладывая силу 100 Н. Какая работа A была совершена при растяжении пружины?
99. Чтобы растянуть пружину на 30 см , потребовалось совершить работу 15 Дж. Какую силу надо прикладывать, чтобы удерживать пружину в растянутом состоянии?
100. Докажите, что работа, которую необходимо совершить для растяжения пружины, прямо пропорциональна квадрату величины удлинения пружины.
101. Пружину растянули на 1 см , а потом – еще на 1 см . При каком из этих действий пришлось совершить большую работу? Во сколько раз?
102. Чтобы растянуть пружину на 3 см , надо совершить работу 30 Дж. На сколько растянулась бы пружина, если бы совершили работу 120 Дж?
103. Пружину динамометра медленно растягивают. К моменту, когда динамометр показывает 20 Н, совершена работа 1 Дж. Какую работу надо совершить, чтобы показание динамометра увеличилось от 30 Н до 50 Н?
104. Какую работу надо совершить, чтобы вытащить пробку из трубки, двигая ее вправо, если для того, чтобы пробка сдвинулась, надо приложить силу 20 Н? Как изменится ответ, если пробку надо вытащить, двигая ее влево? Считайте, что сила трения, действующая на пробку со стороны трубки, пропорциональна плошали соприкосновения пробки и трубки. Длина пробки 10 см , а расстояние до края бутылки 5 см .
105. Гвоздь длиной 10 см забит по шляпку в доску толщиной 4 см . Какую работу надо совершить, чтобы вытащить гвоздь, если в начале вытаскивания надо приложить силу 20 Н?
106. На поверхности воды в озере плавает толстая доска. В каком случае придется совершить большую работу: поднимая доску настолько, чтобы ее нижняя сторона касалась воды, или погружая ее настолько, чтобы доска погрузилась в воду полностью? Плотность древесины 500 кг/м .
107. В озере плавает плоская льдина. В каком случае придется совершить большую работу: поднимая льдину настолько, чтобы ее нижняя сторона касалась воды или погружая ее настолько, чтобы льдина погрузилась в воду полностью? Во сколько раз одна работа больше другой?
108. На дне большого аквариума лежит алюминиевый куб с длиной ребра 10 см . Глубина воды в аквариуме 20 см . Какую работу надо совершить, чтобы поднять куб на 10 см ? Еще на 10 см ? Еще на 10 см ? Изменением уровня воды в аквариуме можно пренебречь.
109. На дне озера лежит бетонная плита толщиной 0,5 м и массой 5 т. Ее подняли так, что ее нижняя грань находится на высоте 1 м над поверхностью воды. Какай работа совершена при этом, если глубина озера 2 м ?
110. Легкий сплошной конус погружают в воду один раз вершиной вверх, а другой раз – вершиной вниз. В каком случае надо совершить большую работу для полного погружения конуса? Одинаковые ли по модулю силы Архимеда
111.В воду опущен нижний край длинной вертикальной трубы. Плотно прилегающий к стенкам трубы легкий поршень площадью 100 см P 2 P может перемещаться вдоль трубы с очень малым трением. Какую работу A , необходимо совершить, чтобы поднять поршень на высоту 10 м от поверхности воды? Какова будет работа при подъеме поршня на высоту 20 см ?
112. Шнур, лежащий на нижнем горизонтальном участке гладкой, поверхности, надо перетянуть на горку так, чтобы конец шнура лежал на склоне. Какую наименьшую работу потребуется совершить? Сила F , необходимая для удержания шнура в конечном положении, равна 2 Н, длина склона 1 м , длина шнура 3 м .
113. Какую работу совершает сила давления газов при выталкивании ядра из пушки, если длина ствола 1,6 м , радиус ядра 10 см , а среднее давление в стволе пушки во время выстрела в 2 000 раз больше давления атмосферы?
114. Гибралтарский пролив образовался «всего» около 5 миллионов лет назад, и возникший тогда гигантский водопад начал заполнять бассейн Средиземного моря водой из Атлантического океана. Каждую секунду с высоты 800 м низвергался один миллион кубометров воды. Во сколько раз мощность этого водопада больше мощности крупной современной гидроэлектростанции (8 × 10 P 3 P МВт)?
115. Электромотор поднимает с постоянной скоростью u груз, висящий на тяжелой цепи. Масса груза M , длина цепи l , масса цепи m . Какую мощность N развивает мотор в тот момент, когда груз поднят на высоту x ?
116. Первый мотор поднимает груз массой m B 1 B со скоростью v B 1 B , a второй поднимает груз массой m B 2 B со скоростью v B 2 B . С какой скоростью u будет поднимать груз массой M мотор, мощность которого равна сумме мощностей первых двух моторов?
117. Пружину растянули на 5 см за 3 с. Какую среднюю мощность при этом развивали, если для удержания пружины в растянутом состоянии требуется сила 120 Н?
118. Для откачивания воды из подвала используют насос мощностью 300 Вт. Ширина подвала 6 м , длина 24 м , высота 4 м . Перед началом откачивания уровень воды в подвале находится на уровне земли. Сколько времени займет откачивание? Считайте, что в процессе откачивания мощность насоса оставалась неизменной.
119. Стержень массой 9 кг и длиной 1 м лежит на двух опорах. Одна из них находится у левого края стержня, а другая – на расстоянии 10 см от правого края. С какой силой действует на стержень каждая из опор?
120. Однородный стержень длиной 1 м подвешен горизонтально на двух динамометрах. Первый динамометр находится на расстояния 10 см от левого конца стержня и показывает 20 Н, второй динамометр находится на расстоянии 30 см от правого конца. Какова масса стержня?
121. К однородной балке массой 400 кг и длиной 7 м подвешен груз массой 700 кг на расстоянии 2 м от одного из концов. Балка концами лежит на опорах. Какова сила давления на каждую из опор?
122. К концам рычага длиной 50 см подвешены медный и серебряный сплошные шары одинакового объема. На каком расстояний от середины рычага надо разместить точку опоры, чтобы рычаг находился в равновесии?
123. Прямолинейный кусок проволоки массой 40 г подвешен за середину. Левую половину куска согнули пополам. Какой массы груз надо подвесить к согнутому колену, чтобы восстановить равновесие?
124. Деревянная палочка подвешена за верхний конец, а нижний ее конец находится в воде. Равновесие наступает тогда, когда в воде находится половина палочки. Какова плотность древесины?
Источник: gitara.ucoz.com
Задача в бассейне плавает лодка как изменится уровень
Задача в бассейне плавает лодка как изменится уровень


2017-10-05
В бассейне плавает лодка. Как изменится уровень воды в бассейне, если из лодки в бассейн бросить камень? Что произойдет с уровнем воды в бассейне, если в днище лодки проделать отверстие и лодка начнет погружаться? Если уровень воды в бассейне при этом изменится, то в какой момент начнется изменение?
Если камень из лодки выбросить на берег бассейна, то уровень воды в бассейне понизится. Это происходит потому, что лодка становится легче, она всплывает и объем вытесняемой ею воды уменьшается.
Уровень воды в бассейне понизится и в том случае, когда камень выбрасывают в бассейн, хотя понижение уровня теперь будет несколько меньше. В самом деле, когда камень лежит на дне, вытесняемый им объем воды равен объему камня. Пока же он находился в лодке, лодка вытесняла дополнительный объем воды, масса которого была равна массе камня. Так как плотность камня больше плотности воды, то этот объем больше объема самого камня.
А что если из лодки в бассейн выбросить деревянный предмет, например бревно? Если бревно выбрасывается на берег, то тогда нет никакой принципиальной разницы со случаем, когда выбрасывается камень: уровень воды в бассейне понизится. Совсем другое дело, когда бревно выбрасывают в воду. В этом случае уровень воды в бассейне останется прежним, хотя лодка, конечно, несколько всплывет. Ведь бревно плавает на поверхности и, значит, вытесняет такой же объем воды, какой раньше (т. е. до выбрасывания бревна) дополнительно вытесняла лодка.
Итак, если выброшенный из лодки в воду предмет плавает, то уровень воды в бассейне остается без изменения. Если же предмет тонет в воде, то уровень воды понижается.
К этим же выводам можно прийти и проще, если представить себе, что весь бассейн стоит на весах. Что бы мы ни выбрасывали из лодки в воду, показания весов, конечно, не изменятся. Поэтому если выброшенные из лодки предметы плавают на поверхности, то сила давления воды на дно бассейна не должна измениться. А это возможно только тогда, когда уровень воды останется прежним.
Если же выброшенный предмет опустился на дно бассейна, то действующая на дно бассейна сила определяется не только гидростатическим давлением воды, но и действием самого предмета. Так как полная сила должна остаться прежней, то сила давления воды на дно должна уменьшиться. Поэтому уровень воды в бассейне понизится.
Теперь, когда мы разобрались с первым вопросом, не составит большого труда ответить на вопрос, будет ли изменяться уровень воды в бассейне, если в днище лодки проделать отверстие. Будем считать, что заполнение лодки водой через отверстие происходит медленно, небольшими порциями, так что пока лодка не утонет, она в каждый момент находится в равновесии на поверхности воды.
Пока лодка находится на плаву, уровень воды в бассейне не меняется. Объем погруженной части лодки увеличивается ровно на столько, сколько воды (по объему) вошло в лодку. В некоторый момент, набрав определенное количество воды, лодка уже не сможет оставаться в равновесии на плаву и начнет погружаться на дно. С этого момента и произойдет понижение уровня воды в бассейне.
Эта задача знаменита тем, что при попытке сразу ответить на поставленные вопросы интуиция часто подводит, так что даже некоторые очень известные физики давали неправильные ответы.
Учебники
Журнал “Квант”
Общие
Эпштеин В. Метод эквивалентных деформаций //Квант. — 2009. — № 1. — С. 40-41.
По специальной договоренности с редколлегией и редакцией журнала “Квант”
Математика представляет собой естественный язык, на котором формулируются и решаются физические задачи. И, тем не менее, для понимания элементарных (а может быть, и фундаментальных) оснований науки об окружающем нас мире полезно познакомиться с задачами, решение которых не требует проведения математических расчетов. Так, метод эквивалентных деформаций предполагает ряд мысленных изменений конфигурации (т.е. геометрических размеров и формы) тел, при которых основные характеристики системы остаются неизменными, но ход исследуемых процессов становится очевидным. Вашему вниманию предлагается несколько таких задач.
Читать еще: Беседка для дачи без пола своими руками
Задача 1.
В небольшом бассейне плавает лодка. Изменится ли (и если изменится, то как) уровень воды в бассейне, если лежащий на дне лодки камень бросить в воду?
Решение
Расчетные методы решения этой задачи предложены во многих учебных пособиях. Можно, однако, обойтись и без расчетов.
Подумаем: зависит ли ответ на вопрос, поставленный в задаче, от формы дна лодки, на котором лежит камень? Ясно, что такой зависимости быть не может: в законе Архимеда форма тела, погруженного в жидкость, никакой роли не играет. Тогда будем мысленно «продавливать» камень через дно лодки.
Последовательные стадии этого процесса представлены на рисунке 1. На одном из этапов камень можно представить подвешенным на веревке, привязанной ко дну лодки. Уровень воды, естественно, не изменится, если удлинить веревку так, чтобы камень коснулся дна бассейна. Если же веревку теперь перерезать, то, очевидно, лодка всплывет, и, следовательно, уровень воды понизится.
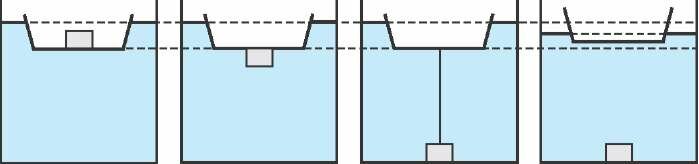
Задача 2.
В стакане плавает кусок льда, содержащий: а) пузырёк, наполненный воздухом; б) кусочек пробки; в) стальную гайку. Как изменится уровень воды в стакане, когда лед растает?
Решение
Заметим для начала, что если лед однороден, то после его таяния уровень воды не изменится: лед вытесняет ровно столько воды, сколько сам весит и, следовательно, сколько получится при плавлении.
Ясно, что решение задачи не зависит от места расположения указанных объектов в куске льда. В случае а), к примеру, пузырек можно переместить к поверхности льда (рис.2). Таким образом, наличие пузырька эквивалентно изменению формы однородного льда, плавление которого, как уже говорилось, уровня воды не изменяет.
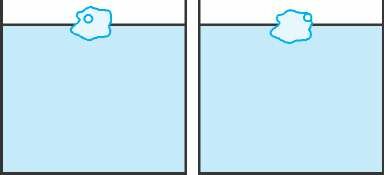
Следует отметить, что, строго говоря, сказанное выше справедливо лишь в том случае, если плотность влажного воздуха в пузырьке совпадает с плотностью окружающего атмосферного воздуха. В состоянии термодинамического равновесия это возможно только в так называемой тройной точке, т.е. при таких значениях температуры и давления, при которых лед, вода и водяной пар находятся в равновесии ((
t approx 0,01 ^cdot C , p approx ^cdot 4,6 )мм рт. ст).
Таяние льда с вмерзшей пробкой – случай б) – уровень воды не изменит, так как пробку можно мысленно выдавить изо льда и пустить в самостоятельное плавание на тонкой ледяной нити.
В случае в) гайку, как и в первой задаче, «продавим» сквозь лед до дна стакана, а затем перережем связывающую ледяную нить. Лед всплывет, уровень воды понизится и уже не изменится после плавления льда.
Задача 3.
Закрытый пробкой сосуд, вес которого равен выталкивающей силе, покоится на дне стакана с водой. Почти не совершая работы, его можно поднять к поверхности воды. Если теперь вынуть пробку, то сосуд наполнится водой и утонет. При этом он может совершить некоторую работу. Если же вынуть пробку, когда сосуд лежит на дне, он также наполнится водой, но работы не совершит.
Как согласовать полученные результаты с законом сохранения энергии?
Решение
Обсудим, в чем суть парадокса.
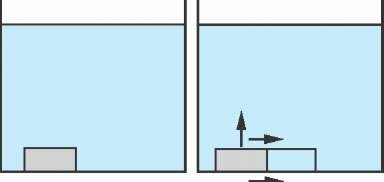
В первой части задачи речь идет о том, что при падении сосуда, заполненного водой, работа совершается несмотря на то, что для поднятия тела не пришлось затратить никакой энергии. Произведем, однако, с сосудом в исходном состоянии эквивалентную деформацию: мысленно деформируем лежащий на дне сосуд так, как показано на рисунке 3. «Выдавим» массу стенок в перемещенную часть, а пустую часть сосуда отделим от заполненной.
Вода окажется «захваченной» стенками сосуда и, таким образом, будет находиться внутри сосуда. Теперь сосуд и «воздух» можно поднимать раздельно. Поднимая сосуд, мы совершаем работу. Поднятие «воздуха» эквивалентно опусканию некоторого объема воды (массы этой воды и сосуда равны). Ситуация совершенно аналогична повороту равно-плечного рычага с равными грузами на концах.
Поднимая один груз, мы опускаем другой (рычаг находится в положении безразличного равновесия – работа не совершается). Затем мы можем перерезать нить, которой привязан поднятый груз. При падении этого груза сила тяжести совершит работу.
Читать еще: Где устанавливают воздушный клапан для канализации
Применяя этот же метод во второй части задачи, мы не видим существенных различий с уже рассмотренным случаем. Наполнение водой сосуда эквивалентно перемещению известного объема воды от поверхности до дна стакана.
Работа при этом выполняется такая же, что и в первом случае (при перемещении сосуда).
Отличие условий первой части задачи от второй сводится, таким образом, всего лишь к порядку действий. Нарушения закона сохранения энергии не обнаруживается.
Задача 4.
Сосуд наполовину заполнен водой, в которой плавает кусок льда. Поверх льда наливают керосин, верхний уровень которого устанавливается на высоте h от дна сосуда. Как изменится эта высота, когда лед растает?
Решение
Эта задача была опубликована в «Задачнике «Кванта» (Ф113) в 1971 году. В журнале приведено строгое математическое решение этой (не очень сложной) задачи. Можно, однако, обойтись и без расчетов.
В случае, когда лед оказывается под поверхностью керосина, ответ очевиден: вода, полученная после плавления льда, занимает меньший объем, значит, верхний уровень керосина понизится.
Интерес представляет анализ ситуации, когда лед выступает над поверхностью керосина. Идея эквивалентных деформаций порождает соблазн деформировать лед так, чтобы его вершина оказалась под поверхностью керосина. Таким образом, казалось бы, можно свести рассматриваемую задачу к предыдущей. Однако этот «фокус» не проходит: погружение выступающей части льда в керосин сопровождается повышением уровня жидкости, а после плавления уровень понижается – следовательно, конечный результат не будет очевидным. Итак, деформация оказывается неэквивалентной.
Но если эквивалентная деформация льда не проходит, не стоит ли двинуться в противоположном направлении: оставить лед в покое, а «деформировать» жидкости? Попробуем.
Для этого слой керосина толщиной H 1 заменим таким слоем воды, который сохраняет положение льда неизменным (рис.4). Поскольку плотность воды больше плотности керосина, высота этого слоя H 2 1 . При плавлении льда уровень воды (как было замечено выше) не меняется. Если теперь осуществить обратную замену и вернуть на место керосин (для этого следует оставить след поверхности льда, как показано на рисунке 5), то выяснится, что слой керосина над поверхностью, которую ранее образовывала вода, растекается по большей площади и уровень керосина понижается (по сравнению с исходным).
Как изменится уровень воды в бассейне?
В небольшом бассейне плавает резиновая лодка, в которой лежат камень и бревно. Как изменится уровень воды в бассейне, если эти предметы (по одному) выбрасывать 1) на берег, 2) в бассейн? Эта задача знаменита тем, что даже известные физики, не подумав, давали неправильные ответы!
Если лодка плавает, значит Архимедова сила равна весу лодки, камня, бревна. Объем вытесненной воды в этом случае равен весу конструкции деленному на плотность воды и g. 1.Если камень и бревно выбросить на берег, вес конструкции уменьшится, объем вытесненной воды тоже – уровень понизится.2. бревно в воду -все плавает ничего не меняется.3.камень на дно , раньше камень плавал и всем своим весом вызывал Архимедову силу, на дне же эта сила равна объему камня умноженному на плотность воды и g. Остальной вес камня компенсируется реакцией опоры( дна), уровень опять понизится.
Читать еще: Классификация машин для контактной сварки
Если лодка плавает, значит на нее действует архимедова сила. Лодка вытесняет воду масса которой равна массе самой лодки. И равна по объему ее подводной части. Поскольку камень и бревно входят в массу брутто лодки, то масса воды, которую они вытесняют вместе с лодкой равна массе лодки,+ камня,+ бревна.
Если камень выкинуть за борт, то лодка всплывет потеряв массу, а камень вытеснит объем воды равный своему объему. Уровень воды в бассейне не изменится. Однако изменится архимедова сила действующая на лодку. Но это уже другой вопрос. Что касается бревна, то если его выкинуть за борт, лодка еще больше всплывет, лишившись массы.
Однако бревно по прежнему будет вытеснять воду равную своей массе. Уровень в бассейне опять не измениться. Если весь груз выкинуть на берег, то лодка так же всплывет, и перестанет вытеснять воду равную по массе груза. Уровень воды в бассейне понизится из за того, что грузом больше не вытесняется вода.
Правильные ответы уже были. Но были и неправильные. Задача несложная, но можно запутаться. Поэтому хочу только пояснить для остальных возможный ход решения. Если любой предмет выбросить из лодки на берег, то лодка, став легче, будет вытеснять меньше воды, и уровень воды в бассейне понизится.
Если бревно выбросить не на берег, а в воду, ее уровень не изменится: бревно, плавающее в бассейне, будет вытеснять столько же воды, сколько оно вытесняло (своим весом), когда находилось в лодке. С камнем иначе: камень тяжелее воды, поэтому на дне он вытесняет меньше воды, чем когда находится в лодке; уровень воды в бассейне в этом случае тоже понизится. Действительно, пусть масса камня 2 кг, а его плотность 2 кг/дм3, тогда объем камня 1 дм3. Камень в лодке вытесняет дополнительно 2 дм3 (2 л) воды, а на дне — только 1 дм3 (1 л).
Если решать при помощи математики и нехитрых рассуждений и рассматривать исходное состояние (1) и конечное состояние с выброшенным из лодки в воду бассейна камнем (2), то получается: Vлодки1=Vвоздуха1+Vкамня; Vлодки2=Vвоздуха2. Здесь необходимо добавить, что в качестве объема лодки и воздуха в лодке мы берем объем до ватерлинии.
Тогда изменение объема лодки: измVлодки=Vлодки1-Vлодки2=Vвоздуха1+Vкамня-Vвоздуха2=измVвоздуха+Vкамня. Возьмем объем воды водоема без лодки как Vбасс.
Теперь поскольку нас интересует изменение уровня воды в водоеме, а показателем объема водоема является сумма объема воды в бассейне и объема помещенных в воду предметов, здесь мы будем рассматривать в качестве объема водоема в ситуациях 1 и 2 суммарную величину объема воды бассейна, объема добавляемого лодкой и объема камня (для случая 2): Vбасс1=Vбасс+Vлодки1, Vбасс2=Vбасс+Vлодки2+Vкамня. Теперь найдем изменение объема водоема: измVбасс=Vбасс1-Vбасс2=Vлодки1-Vлодки2-Vкамня=измVлодки-Vкамня= =измVвоздуха+Vкамня-Vкамня=измVвоздуха. То есть у нас измVбасс=измVвоздуха, иначе говоря объем водоема меняется ровно настолько, насколько изменился объем вытесняемого лодкой воздуха. Теперь все по полочкам, и с бревном понятно становится – уровень воды останется тот-же.
Выбрасываем на берег камень. Вес лодки уменьшается, уровень повышается. Выбрасываем дерево на берег. Уровень повышается. В этом случае реакция уровня одинакова на камень и дерево. Теперь выбросим камень в воду. Он утонул. Уровень воды уменьшится, потому что удельный вес камня больше удельного веса воды. Выбрасываем дерево, оно не тонет, поэтому уровень не изменится.
Можно произвести точные расчеты с учетом удельного веса воды и камня.
Источник: detoxlife-moscow.ru