Длиной волны называют кратчайшее пространственное расстояние между ее точками, совершающими колебания в одной фазе. Обозначают длину волны, чаще всего буквой $lambda$ .
Для синусоидальных волн $lambda$ – это расстояние, на которое волна распространяется за один период (T). Длину волны в этом случае еще называют пространственным периодом. Тогда формулой длины волны можно считать выражение:
где v – скорость распространения волны, $nu=frac$ – частота колебаний, $k=frac<omega>$ – волновое число, $T=frac<omega>$ – период волны, $omega$ – циклическая частота волны.
Длина стоячей волны
Длиной стоячей волны($lambda_$) называют расстояние в пространстве между двумя пучностями (или узлами):
где $lambda$ – длина бегущей волны. Надо заметить, что расстояние между соседними пучностью и узлом связывает равенство:
Длина бегущей волны
В бегущей волне длина волны связана с фазовой скоростью (vph) формулой:
Длина бегущей волны
Разность фаз и длина волны
Урок 370. Механические волны. Математическое описание бегущей волны
Две точки волны находящиеся на расстоянии $Delta x$ имеют при колебании разность фаз ($Delta varphi$), которая равна:
Длина электромагнитной волны
Скорость распространения электромагнитных волн в вакууме равна скорости света в вакууме ($c approx 3 cdot 10^$ м/с), следовательно, длина электромагнитной волны в вакууме, может быть рассчитана при помощи формулы:
Длина электромагнитной волны в веществе равна:
где $n=sqrt$ – показатель преломления вещества, $varepsilon$ – диэлектрическая проницаемость вещества, $mu$ – магнитная проницаемость вещества.
Отметим, что все рассматриваемые формулы относят к случаю T=const.
Единицы измерения длины волны
Основной единицей измерения длины волны в системе СИ является: [$lambda$]=м
Примеры решения задач
Задание. Каково приращение длины электромагнитной волны, имеющей частоту v=1 МГц при ее переходе в немагнитную среду, которая имеет диэлектрическую проницаемость $varepsilon$=2?
Решение. Так как речь в условии задачи идет о немагнитной среде, в которую переходит волна, то считаем магнитную проницаемость вещества равной единице ($mu$=1).
Длина рассматриваемой нами волны в вакууме равна:
Длина волны в веществе:
Используя выражения (1.1) и (1.2) найдем изменение длины волны:
Проведем вычисления, если нам известно помимо данных приведенных в условии задачи, что $c approx 3 cdot 10^$ м/с- скорость света в вакууме, и v=1 МГц=10 6 Гц:
Ответ. Длина волны уменьшится на 150 м

проверенных автора готовы помочь в написании работы любой сложности
Механические колебания и волны
Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Урок 372. Скорость продольной волны в стержне. Скорость звука в жидкостях и газах.
Отличительными признаками колебательного движения являются:
- повторяемость движения;
- возвратность движения.
Для существования механических колебаний необходимо:
- наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
- наличие малого трения в системе.
Механические волны – это процесс распространения колебаний в упругой среде.

Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.
- Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.

Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.
Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.
Гармонические колебания
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:
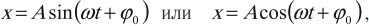
где ( x ) – координата тела – смещение тела от положения равновесия в данный момент времени; ( A ) – амплитуда колебаний; ( omega t+varphi_0 ) – фаза колебаний; ( omega ) – циклическая частота; ( varphi_0 ) – начальная фаза.
Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
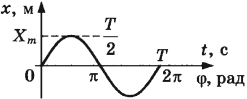
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.
Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:
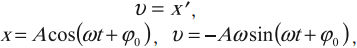
где ( v ) – мгновенное значение скорости, т. е. скорость в данный момент времени.
Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:
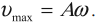
Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:
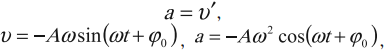
где ( a ) – мгновенное значение ускорения, т. е. ускорение в данный момент времени.
Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:
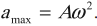
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:
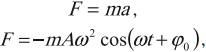
где ( F ) – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.
Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
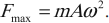
Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:
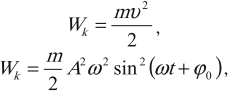
где ( W_k ) – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.
Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
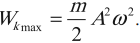
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:
- потенциальная энергия равна нулю;
- кинетическая энергия максимальна.
При максимальном отклонении от положения равновесия:
- кинетическая энергия равна нулю;
- потенциальная энергия максимальна.
Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:
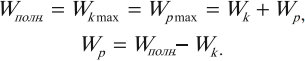
Важно!
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.
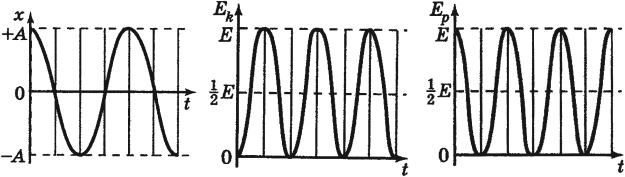
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.
Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).
Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ( A, (X_) ) , единицы измерения – м.
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ( varphi ) , единицы измерения – рад (радиан).
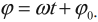
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
( varphi_0 ) – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Период колебаний
Период колебаний – это время одного полного колебания.
Обозначение – ( T ) , единицы измерения – с.

Период гармонических колебаний – постоянная величина.
Частота колебаний
Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ( nu ) , единицы времени – с -1 или Гц (Герц).
1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:

Период и частота колебаний – взаимно обратные величины:

Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ( omega ) , единицы измерения – рад/с.

Свободные колебания (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
- при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
- силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
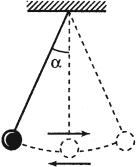
Период колебаний математического маятника:
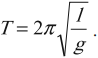
Частота колебаний математического маятника:
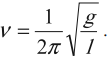
Циклическая частота колебаний математического маятника:
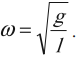
Максимальное значение скорости колебаний математического маятника:
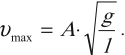
Максимальное значение ускорения колебаний математического маятника:
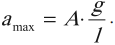
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
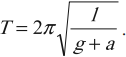
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
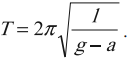
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
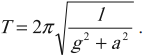
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ( h ) , определяется по формуле:
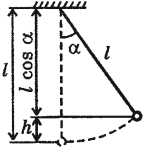
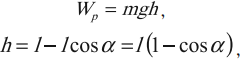
где ( l ) – длина нити, ( alpha ) – угол отклонения от вертикали.
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
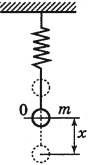
Период колебаний пружинного маятника:
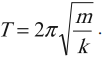
Частота колебаний пружинного маятника:
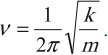
Циклическая частота колебаний пружинного маятника:
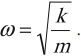
Максимальное значение скорости колебаний пружинного маятника:
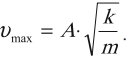
Максимальное значение ускорения колебаний пружинного маятника:
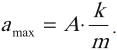
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
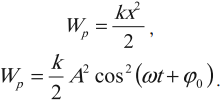
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
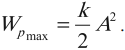
Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.
Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
Резонанс
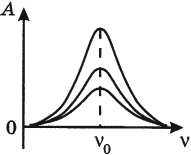
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
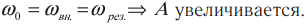
( v_0 ) – собственная частота колебаний маятника.
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.
Длина волны
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ( lambda ) , единицы измерения – м.
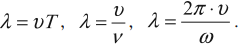
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
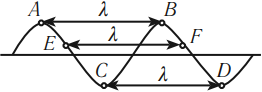
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук ( ( nu ) < 16 Гц);
- звуковой диапазон (16 Гц < ( nu ) < 20 000 Гц);
- ультразвук ( ( nu ) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
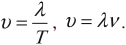
Скорость звука зависит
- от упругих свойств среды:
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
- от температуры среды:
в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.
Источник: fizi4ka.ru
2. Распространение звука. Звуковые волны
Наше ухо постоянно слышит различные звуки. Чаще всего звук распространяется по воздуху, но может распространяться и в других средах. Эти среды называют упругими.
Если между ухом и источником звука удалить звукопередающую среду, то мы ничего не услышим. Это означает, что для передачи звука на расстояние необходима звукопередающая среда.
Чтобы изолировать источник звука (будильник) от звукопередающей среды (воздуха), поместим его в установку, где сможем откачать воздух (рис. (1)).

Рис. (1). Эксперимент с будильником в вакууме
Для чистоты эксперимента послушаем будильник в воздушной среде под колоколом воздушного насоса. Звук слышен очень хорошо. Постепенно начнём откачивать воздух. Громкость звука уменьшается. При достижении вакуума под колоколом звук перестаёт передаваться — будильник не слышно.
Этим экспериментом мы подтвердили утверждение о том, что в отсутствие упругой среды звук не передаётся.
Звуковые волны распространяются в упругой среде. Чем больше плотность вещества, тем лучше оно проводит звук.
Проведём эксперимент с доской из древесины (рис. (2)). Сможем ли мы расслышать тиканье часов на расстоянии, приложив ухо к одному концу доски, а к другому — наручные часы? Звук хорошо передаётся по доске.

Рис.(2). Эксперимент с доской из древесины
Если подвесить металлическую ложку на верёвочке (рис. (3)) и привязать другой конец к пальцам, то вибрация будет им передаваться. Проволока из металла будет лучше проводить звук.

Рис. (3). Эксперимент с ложкой и верёвочкой
Тела с низкой плотностью, не обладающие упругостью, содержащие звукоизолирующие слои (например, прослойку воздуха) проводят звук в меньшей степени. Например, пробка, поролон, вата.
Чтобы изолировать помещение от посторонних или ненужных звуков, необходимо облицевать потолок, стены и даже пол различными звукопоглощающими материалами. Для этих целей используют минеральную, базальтовую или хлопковую вату, а также газостекло, пенобетон, вспененный полиуретан и меламин и др. Все эти материалы в порах содержат воздух, что и способствует поглощению звука.
Таким образом,
звук может распространяться в любой среде (твёрдой, жидкой и газообразной), где есть молекулы. И не может распространяться там, где молекул нет, т.е. в вакууме.
Колебания источника звука создают в окружающей среде волну звуковой частоты, которая является упругой волной.
Восприятие звука слуховым аппаратом (рис. 4):
- Волна, достигая наружного уха, воздействует на барабанную перепонку, что заставляет её колебаться с точно такой же частотой, с какой колеблется источник звука.
- Колебания барабанной перепонки передаются на слуховые косточки в среднем ухе, далее — во внутреннее ухо.
- Во внутреннем ухе колебания воздействуют на улитку, в которой есть волосковые клетки, которые преобразуют механические колебания в электрические нервные импульсы.
- Слуховой нерв передаёт электрические нервные импульсы от улитки в головной мозг.
- Мозг анализирует сигналы: распознаёт, сравнивает, интерпретирует.

Рис. (4). Строение слухового аппарата
В газах и жидкостях могут существовать только продольные упругие волны. Поэтому звук в воздухе передаётся продольными волнами, то есть чередующимися сгущениями и разрежениями воздуха, идущими от источника звука.
Звуковая волна распространяется в пространстве с определённой скоростью.
Наблюдая за стрельбой из оружия (например, из пушки), мы сначала видим вспышку и только потом (через некоторое время) слышим звук выстрела.
Измерив промежуток времени (t) между моментом появления вспышки и моментом, когда звук доходит до уха, а также расстояние между источником звука и наблюдателем, можно определить скорость распространения звука по формуле:
По опытным данным, при нормальном атмосферном давлении и температуре воздуха (0) °С скорость звука составляет (332) м/с.
В газах скорость звука прямо пропорциональна температуре.
Например, при (20) °С скорость звука в воздухе равна (343) м/с, при (60) °С — (366) м/с, при (100) °С — (387) м/с.
При повышении температуры среды увеличивается скорость движения молекул (или атомов) среды, что повышает интенсивность взаимодействия частиц среды. Значит, увеличивается передача энергии колебательного движения.
На скорость распространения звука оказывает влияние среда, в которой распространяется звук. Это связано не только с плотностью среды, но и расположением частиц этой среды относительно друг друга.
При решении задач скорость звука в воздухе обычно считают равной (340) м/с.
При температуре (0) °С скорость звука в водороде равна (1284) м/с, а в углекислом газе — (259) м/с. Это различие связано с массой молекул газов, в которых распространяется звук. Масса молекул водорода меньше массы молекул углекислого газа.
Для измерения скорости звука существуют специальные устройства, принцип действия которых связан с определением времени, за которое звук проходит определенное расстояние.
Плотности жидкостей и твёрдых тел значительно больше плотностей газов. Поэтому молекулы в этих средах находятся значительно ближе друг к другу, а следовательно, взаимодействие между ними более сильное. Это способствует более быстрому распространению звука.
Источник: www.yaklass.ru