Лодка качается на волнах с частотой 0 5 гц какова

Кубическая функция

27967 На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: FA = ρgl 3 , где l — длина ребра куба в метрах, ρ = 1000 кг/м 3 — плотность воды, а g — ускорение свободного падения (считайте g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78 400 Н? Ответ выразите в метрах.

27968 На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: FA = αρgr 3 , где α = 4,2 — постоянная, r — радиус аппарата в метрах,ρ = 1000 кг/м 3 — плотность воды, а g — ускорение свободного падения (считайте g = 10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах.

ЕГЭ Физика A2F1EB простое решение задачи без применения формул

Функция четвертой степени

27969 Для определения эффективной температуры звeзд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела P, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвeртой степени температуры: P =σST 4 , где σ = 5,7 · 10 -8 — постоянная, площадь S измеряется в квадратных метрах, а температура T — в градусах Кельвина. Известно, что некоторая звезда имеет площадь S = 1/16 · 10 20 м 2 , а излучаемая ею мощность P не менее 9,12 · 10 25 Вт. Найдите температуру этой звезды в градусах Кельвина.

Дробно-рациональная функция

27970 Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 30 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d2 от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение:

Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.

27971 Перед отправкой тепловоз издал гудок с частотой f0 = 440 Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону:

(Гц), где c — скорость звука в звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с.

Урок 94 (осн). Задачи на колебательное движение

27972 По закону Ома для полной цепи сила тока, измеряемая в амперах, равна

где ε — ЭДС источника (в вольтах), r = 1 Ом — его внутреннее сопротивление,R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания:

Ответ выразите в омах.

27973 Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: I = U/R, где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.

27974 Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле:

где ω — частота вынуждающей силы (в с -1 ), А0 — постоянный параметр,

— резонансная частота. Найдите максимальную частоту ω , меньшую резонансной, для которой амплитуда колебаний превосходит величину А0 не более чем на 12,5% . Ответ выразите в с -1 .

27975 В розетку электросети подключены приборы, общее сопротивление которых составляет R1= 90 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R2 этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R1 Ом и R2 Ом их общее сопротивление задаeтся формулой:

(Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в омах.

27976 Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой:

где T1 — температура нагревателя (в кельвинах), T2 — температура холодильника (в кельвинах). При какой температуре нагревателя T1 КПД этого двигателя будет 15%, если температура холодильника T2 = 340 К? Ответ дайте в кельвинах.

27977 Коэффициент полезного действия (КПД) кормозапарника равен отношению количества теплоты, затраченного на нагревание воды массой mв (в килограммах) от температуры t1 до температуры t2 (в градусах Цельсия) к количеству теплоты, полученному от сжигания дров массы mдр кг. Он определяется формулой:

где cв = 4,2· 10 3 Дж/(кг·К) — теплоёмкость воды, Дж/кг — удельная теплота сгорания дров. Определите массу дров, которое понадобится сжечь в кормозапарнике, чтобы нагреть m = 83 кг воды от 10º C до кипения, если известно, что КПД кормозапарника равен 21%. Ответ выразите в килограммах.

27978 Опорные башмаки шагающего экскаватора, имеющего массу m = 1260 тонн представляют собой две пустотелые балки длиной l = 18 метров и шириной s метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой:

где m — масса экскаватора (в тоннах), l — длина балок в метрах, s — ширина балок в метрах, g — ускорение свободного падения (считайте g=10 м/с 2 ). Определите наименьшую возможную ширину опорных балок, если известно, что давление p не должно превышать 140 кПа. Ответ выразите в метрах.

27979 К источнику с ЭДС ε = 55 В и внутренним сопротивлением r = 0,5 Ом, хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, задаeтся формулой:

При каком наименьшем сопротивлении нагрузки напряжение на ней будет не менее 50 В? Ответ выразите в омах.

27980 При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу, частота звукового сигнала, регистрируемого приёмником, не совпадает с частотой исходного сигнала f0 = 150 Гц и определяется следующим выражением:
(Гц), где c — скорость распространения сигнала в среде (в м/с), а u=10 м/с и v=15 м/с — скорости приёмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет не менее 160 Гц?

27981 Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость спуска батискафа, выражаемая в м/с, определяется по формуле:

где c =1500 м/с — скорость звука в воде, f0 — частота испускаемых импульсов (в МГц), f — частота отражeнного от дна сигнала, регистрируемая приeмником (в МГц). Определите частоту отраженного сигнала в МГц, если скорость погружения батискафа равна 2 м/с.

27988 Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле:

где m = 1200 кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного падения g=10 м/с 2 , а π = 3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400000 Па. Ответ выразите в метрах.

27989 Автомобиль, масса которого равна m = 2160 кг, начинает двигаться с ускорением, которое в течение t секунд остаeтся неизменным, и проходит за это время путь S = 500 метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно:

Определите наибольшее время после начала движения автомобиля, за которое он пройдeт указанный путь, если известно, что сила F, приложенная к автомобилю, не меньше 2400 Н. Ответ выразите в секундах.

317097 Рейтинг R интернет-магазина вычисляется по формуле:

rпок — средняя оценка магазина покупателями, rэкс — оценка магазина, данная экспертами, K — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 24, их средняя оценка равна 0,86, а оценка экспертов равна 0,11.

317096. Независимое агентство намерено ввести рейтинг новостных изданий на основе показателей информативности In, оперативности Op и объективности Tr публикаций. Каждый отдельный показатель — целое число от -2 до 2. Составители рейтинга считают, что информативность публикаций ценится втрое, а объективность — вдвое дороже, чем оперативность. Таким образом, формула приняла вид

Найдите, каким должно быть число A, чтобы издание, у которого все показатели максимальны, получило бы рейтинг 30.

319860 Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Q. Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от -2 до 2.

Составители рейтинга считают, что объективность ценится втрое, а информативность публикаций — впятеро дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид:

Если по всем четырем показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число A, при котором это условие будет выполняться.

Источник: chemege.ru

Период и частота колебаний. Циклическая частота

Единица измерения периода в системе СИ – секунда.

На графике колебаний период определяется как промежуток времени. через который система возвращается в то же состояние, в котором она находилась в начальный момент времени, который выбирается произвольно (рис.1).

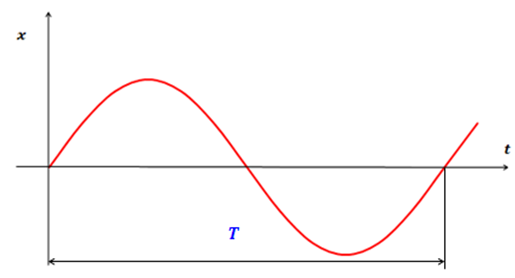
Рис.1. Определение по графику периода колебаний.

ОПРЕДЕЛЕНИЕ
Частота колебаний – это число колебаний, совершаемых телом в единицу времени:

Единица измерения частоты в системе СИ – 1 Герц (Гц).

ОПРЕДЕЛЕНИЕ

Циклическая частота – это число колебаний, совершаемых телом за секунд:

Единица измерения циклической частоты в системе СИ — рад/с.

Частота и циклическая частота связаны между собой формулой:

Примеры решения задач

Задание	Определить частоту колебаний железнодорожных вагонов, если период их вертикального колебания равен 0,5 с.
Решение	Частота колебаний – это величина, обратная периоду:

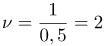
Гц

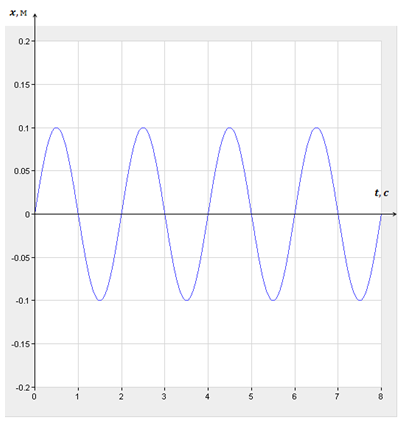
Задание	Маятник совершает 9 колебаний за 18 с. Определить период и частоту колебаний. Записать уравнение гармонических колебаний и построить график колебаний маятника, если амплитуда равна 10 см.
Решение	Частота колебаний определяется формулой:

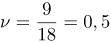
Гц

В данном случае:

Задание	Период колебаний крыльев шмеля 5 мс, а частота колебаний крыльев комара 600 Гц. Определить, какое насекомое и на сколько больше сделает взмахов крыльями при полете за 1 минуту.
Решение	Определим частоту колебаний крыльев шмеля:

С другой стороны, частота:

Приравняв правые части равенств, найдем число взмахов крыльями, которое сделает шмель за время :

Число взмахов крыльями, которое сделает комар за время , найдем непосредственно из формулы:

Переведем единицы в систему СИ: мс мин .

Источник: ru.solverbook.com

Формула частоты

Частота — это физический параметр, которые используют для характеристики периодических процессов. Частота равна количеству повторений или свершения событий в единицу времени.

Чаще всего в физике частоту обозначают буквой $nu ,$ иногда встречаются другие обозначения частоты, например $f$ или $F$.

Частота (наряду со временем) является самой точно измеряемой величиной.

Формула частоты колебаний

При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$

Частота, в этом случае — это число полных колебаний ($N$), совершающихся за единицу времени:

где $Delta t$ — время за которое происходят $N$ колебаний.

Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:

Герц — это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.

Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами ($_1 и _2$) равна:

Еще одно величиной характеризующей колебательный процесс является циклическая частота ($<omega >_0$), связанная с частотой как:

Циклическая частота измеряется в радианах, деленных на секунду:

Частота колебаний тела, имеющего массу$ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:

Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.

Для математического маятника частоту колебаний вычисляют как: длина нити:

где $g$ — ускорение свободного падения; $ l$ — длина нити (длина подвеса) маятника.

Физический маятник совершает колебания с частотой:

где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.

Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.

Формулы для вычисления частоты дискретных событий, частота вращения

дискретных колебаний ($n$) — называют физическую величину, равную числу действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $tau $, то частота дискретных событий равна:

Единицей измерения частоты дискретных событий является обратная секунда:

Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.

Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $tau $ — время, затрачиваемое на один полный оборот, то:

Примеры задач с решением

Задание. Колебательная система совершила за время равное одной минуте ($Delta t=1 мин$) 600 колебаний. Какова частота этих колебаний?

Решение. Для решения задачи воспользуемся определением частоты колебаний: Частота, в этом случае — это число полных колебаний, совершающихся за единицу времени.

Прежде чем переходить к вычислениям, переведем время в единицы системы СИ: $Delta t=1 мин=60 с$. Вычислим частоту:

Ответ. $nu =10Гц$

Задание. На рис.1 изображен график колебаний некоторого параметра $xi (t)$, Какова амплитуда и частота колебаний этой величины?

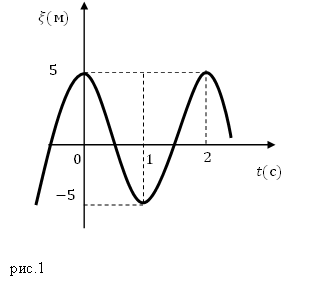
Решение. Из рис.1 видно, что амплитуда величины $xi left(tright)=<xi >_=5 (м)$. Из графика получаем, что одно полное колебание происходит за время, равное 2 с, следовательно, период колебаний равен:

Частота — величина обратная периоду колебаний, значит:

Ответ. 1) $<xi >_=5 (м)$. 2) $nu =0,5$ Гц

проверенных автора готовы помочь в написании работы любой сложности