Какая дробь больше единицы

Неправильные дроби сравниваем по тем же правилам, что и обыкновенные дроби или правильные дроби. Рассмотрим подробно эти правила.

Сравнение неправильных дробей с одинаковыми знаменателями.

Есть несколько правил сравнения неправильных дробей с одинаковыми знаменателями:

1. Если у неправильных дробей положительные числители, то та дробь больше у которой числитель больше.
2. Если у неправильных дробей отрицательные числители, то та дробь больше у которой числитель меньше.
3. Если у неправильных дробей разные знаки, то та дробь больше которая имеет знак “+”.

Рассмотрим пример:
Выполните сравнение неправильных дробей с одинаковыми знаменателями: а) (frac) и (frac) б) (frac) и (frac) г) (frac) и (frac)

Решение:
а) Раз у дробей (frac) и (frac) одинаковые знаменатели переходим к сравнению числителей 20>15,

б) Так как знаменатели у дробей (frac) и (frac) одинаковые сравниваем отрицательные числители. Тот отрицательный числитель больше, который по модулю меньше.

Как быстро сравнить дроби? (Сравнение обыкновенных дробей)

|-161|=161
|-98|=98 меньше по модулю, значит это число ближе к нулю на числовой прямой чем -161, поэтому
-161

г) Сравнивать дроби с разными знаками (frac) и (frac) очень просто, та дробь больше которая имеет знак “+”.

Сравнение неправильных дробей с одинаковыми числителями.

1. Если числители у неправильных дробей одинаковы и положительны, то та дробь больше у которой знаменатель меньше.
2. Если у неправильной дроби числители отрицательные, то та дробь больше у которой знаменатель больше.

Пример:
Выполните сравнение неправильных дробей с одинаковыми числителями: а) (frac) и (frac) б) (frac) и (frac)

Решение:
а) У неправильных дробей с одинаковыми положительными числителями (frac) и (frac), та дробь больше, где знаменатель меньше 9

б) У неправильных дробей с одинаковыми отрицательными числителями (frac) и (frac), та дробь больше где знаменатель больше 3

Сравнение неправильных дробей с разными знаменателями.

Правила сравнения неправильных дробей с разными знаменателями:

1. Привести к общему знаменателю.
2. Переходим к пункту сравнения неправильных дробей с одинаковыми знаменателями.

Рассмотрим пример:
Сравните неправильные дроби с разными знаменателями: а) (frac) и (frac) б) (frac) и (frac) г) (frac) и (frac)

Решение:
а) Приведем дроби (frac) и (frac) к общему знаменателю. Общий знаменатель равен 24.

Сравниваем полученные числители 45>44, следовательно,

б) Найдем общий знаменатель для дробей (frac) и (frac) . Общий знаменатель равен 30.

Сравниваем числители -103

г) Сравниваем числители дробей (frac) и (frac), потому что знаменатель у дробей общий.

Сравнение неправильной дроби с правильной дробью.

1. Если неправильная дробь положительна, то она всегда будет больше правильной положительной дроби.
2. Если неправильная дробь отрицательна, то она всегда будет меньше правильной отрицательной дроби.

Пример:

Сравнение дробей, как узнать какая дробь больше, какая меньше.

Сравните правильную дробь и неправильную дробь: а) (frac) и (frac) б) (-frac) и (-frac)

Решение:
а) Правильная и неправильная дробь положительны, поэтому неправильная дробь больше правильной дроби.

б) Правильная и неправильная дробь отрицательны, поэтому неправильная дробь меньше правильной дроби.

Сравнение неправильных дробей с нулем.

Правила сравнения неправильной дроби с нулем:

1. Если неправильная дробь положительна, то она больше нуля.
2. Если неправильная дробь отрицательна, то она меньше нуля.

Пример:
Сравните неправильную дробь с нулем: а) (frac) и 0 б) 0 и (-frac)

Решение:
а) Неправильная дробь (frac) положительна, поэтому (frac>0)

б) Неправильная дробь (-frac) отрицательна, поэтому (0<-frac)

Сравнение неправильных дробей с единицей.

Правила сравнения неправильной дроби с единицей:

1. Если неправильная дробь положительна, то она больше или равна единице.
2. Если неправильная дробь отрицательна, то она меньше или равна минус единице.

Пример:
Сравните неправильную дробь с единицей: а) (frac) и 1 б) -1 и (frac)

Решение:
а) Неправильная положительная дробь не равная единице всегда больше 1.

б) Дробь (frac= -1), поэтому

Равные неправильные дроби.

Правило равных неправильных дробей:

Неправильные дроби равны тогда, когда при одинаковых знаменателях равны их числители. Например:

Category: 5 класс, Обыкновенные дроби Tag: Сравнение дробей Leave a comment

You may also like:

Сравнение рациональных чисел, определения и примеры.

Добавить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Свежие записи

• Решение линейных уравнений с одной переменной.
• Определение числовой функции. Область определения функции. Область значения функции.
• Определение функции. Способы задания функции.
• Десятичные дроби. Разряды и классы десятичных дробей.
• Что такое уравнение и корни уравнения? Как решить уравнение?

Источник: tutomath.ru

Правильные и неправильные дроби. Сравнение дробей

Может ли числитель дроби быть равным ее знаменателю? Да, может. Действительно, на рисунке 195 прямоугольник разделили на 7 равных частей и все части закрасили. Следовательно, закрашенными оказались $frac$ прямоугольника, т.е. весь прямоугольник. Значит, $frac$ прямоугольника равны 1 прямоугольнику, т.е. $frac$ = 1 .

Рассуждая аналогично, получим, что, например, $frac$ = $frac$ = 1 .

Если числитель дроби равен знаменателю, то дробь равна единице.

В буквенном виде этот вывод можно записать так:

$frac$ = 1

где m − натурально число.

А может ли возникнуть такая «неправильная» ситуация, когда числитель дроби окажется больше знаменателя?

На рисунке 196 изображены два равных прямоугольника, каждый из которых разделен на 7 равных частей. Мы закрасили весь первый прямоугольник и 4 из 7 частей второго прямоугольника. Можно сказать, чтот закрашено $frac$ прямоугольника.

Обратившись к рисунку 197, можно сказать, что гости, пришедшие на день рождения, могут съесть $frac$ праздничного торта.

Дробь, у которой числитель меньше знаменателя, называют правильной.

Дробь, у которой числитель больше знаменателя или равен ему, называют неправильной.

дроби $frac$ , $frac$ , $frac$ − неправильные.

На рисунке 198 изображена точка $C(frac)$ . Если отрезок OC отложить от точки O 11 раз, то получим точку M, координата которой равна $frac$ .

На рисунке 199 закрашено $frac$ прямоугольника. При этом большая часть ( $frac$ прямоугольника) осталась не закрашенной. Тогда можно сделать вывод, что $frac$ > $frac$ .

Этот пример иллюстрирует следующее свойство дробей.

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше, а меньше та, у которой числитель меньше.

Рассмотрим правильную дробь $frac$ и неправильную дробь $frac$ . Сравним эти дроби с единицей. Имеем: $frac$ < $frac$ , т.е. $frac$ < 1, а $frac$ > $frac$ , т.е. $frac$ > 1 .

Эти примеры иллюстрируют следующее свойство.

Все правильные дроби меньше единицы, а неправильные − больше или равны единице.

Это свойство позволяет сделать следующий вывод.

Каждая неправильная дробь больше любой правильной дроби, а каждая правильная дробь меньше любой неправильной дроби.

Отметим, что на координатном луче из двух дробей большая дробь расположена правее меньшей.

Например, точка $D(frac)$ лежит правее точки B( $frac$ ), так как $frac$ > $frac$ (см. рис. 198 ).

Рассмотрим два равных прямоугольника (рис. 200 ) и закрасим $frac$ одного прямоугольника и $frac$ второго. Видно, что площадь закрашенной части первого прямоугольника больше площади второго прямоугольника. Тогда получаем, что $frac$ > $frac$ .

Этот пример иллюстрирует следующее свойство дробей.

Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

Пример. Найдите все натуральные значения a, при которых одновременно дробь $frac$ будет правильной, а дробь $frac$ − неправильной.

Источник: reshalka.com

Может ли правильная дробь быть больше, чем 1?

Может ли правильная дробь быть больше, чем 1?
Всегда ли неправильная дробь больше, чем 1?

Какая дробь больше, если одна из них правильная, а другая неправильная?

Голосование за лучший ответ
1. нет не может2. 1 = неправильной дроби например 12/12 или неправильная дробь больше чем 1
Источник: сама

1.Нет, так как правильная дробь меньше единицы.
2.Нет, так как неправильная дробь больше единицы или равной ей
3.Неправильная дробь всегда больше 1 (или равна 1), а правильная — меньше 1. Отсюда вывод: неправильная больше.

Источник: Голова,ум 🙂
Похожие вопросы
Ваш браузер устарел

Мы постоянно добавляем новый функционал в основной интерфейс проекта. К сожалению, старые браузеры не в состоянии качественно работать с современными программными продуктами. Для корректной работы используйте последние версии браузеров Chrome, Mozilla Firefox, Opera, Microsoft Edge или установите браузер Atom.

Источник: otvet.mail.ru

Сравнение дробей

Сравнить две дроби — это значит установить, какая из них больше, а какая меньше.

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше, и меньше та, у которой числитель меньше.

Пример:

.

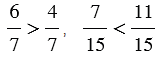
Чтобы сравнить дроби с разными знаменателями, нужно привести их к общему знаменателю.

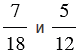
Пример: Сравним дроби: .

Наименьший общий знаменатель данных дробей равен 36. Приведем каждую из дробей к общему знаменателю, для этого найдем к каждой из дробей дополнительный множитель. Для первой дроби дополнительный множитель — 2, т.к. 18 2 = 36, а для второй дроби дополнительный множитель — 3, т.к. 12 3 = 36. Получим:

.

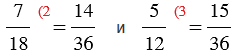
По правилу сравнения дробей с одинаковыми знаменателями 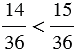, значит, и .

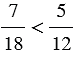Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше, а меньше та, у которой знаменатель больше.

Пример:

.

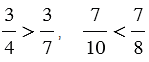
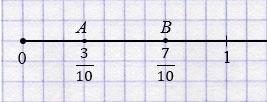
На координатном луче из двух дробей большая расположена правее меньшей.

Пример:

.

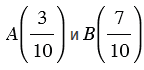
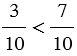
, значит, точка А лежит левее точки В (смотри рисунок ниже).

Если числитель дроби равен знаменателю, то дробь равна единице, т.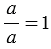е. , где 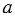— натуральное число.

Пример:

.

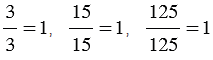
Любая правильная дробь меньше единицы, а любая неправильная дробь больше или равна единице.

Пример:

.

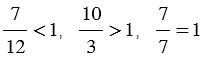
Каждая неправильная дробь больше любой правильной, а каждая правильная дробь меньше любой неправильной дроби.

Пример:

.

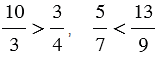
Поделись с друзьями в социальных сетях:

Источник: budu5.com

§26. Правильные и неправильные дроби. Сравнение дробей — Ответы (ГДЗ) к учебнику по математике 5 класс (Мерзляк Полонский Якир)

Правильная дробь — это дробь, у которой числитель меньше знаменателя.

3. Какую дробь называют неправильной.

Неправильная дробь — это дробь, у которой числитель больше знаменателя или равен ему.

4. Какая из двух дробей с равными знаменателями больше? Меньше?

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше; и меньше та, у которой числитель меньше.

5. Сравните с единицей любую правильную дробь; любую неправильную дробь.

Любая правильная дробь меньше единицы, а любая неправильная дробь больше или равна единице.

6. Сравните любую неправильную дробь с любой правильной дробью.

Каждая неправильная дробь больше любой правильной, а каждая правильная дробь меньше любой неправильной дроби.

7. Какая из двух дробей с одинаковыми числителями больше? Меньше?

Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше; а меньше та, у которой знаменатель больше.

РЕШАЕМ УСТНО

1. Какую часть составляет: 1) длина стороны квадрата от его периметра; 2) секунда от часа; 3) угол, градусная мера которого равна 150, от прямого угла; 4) угол, градусная мера которого равна 200, от развернутого угла?

2. Дима находится в школе с 8 ч 30 мин до 14 ч 30 мин. Какую часть суток Дима проводит в школе?

3. Ваня собрал 35 грибов, из которых 4/7 составляют белые. Сколько белых грибов собрал Ваня?

4. В саду растет 36 вишневых деревьев, что составляет 4/9 всех деревьев. Сколько деревьев растет в саду?

5. Пешеход и велосипедист отправились навстречу друг другу из двух поселков, расстояние между которыми равно 28 км. Пешеход до встречи прошел 2/7 пути. Сколько километров проехал до встречи велосипедист?

УПРАЖНЕНИЯ

719. Запишите все правильные дроби со знаменателем 8.

720. Запишите все правильные дроби со знаменателем 11.

721. Запишите все неправильные дроби с числителем 8.

722. Запишите все неправильные дроби с числителем 11.

723. Сравните числа:

724. Сравните числа:

725. Расположите дроби в порядке убывания:

726. Расположите дроби в порядке возрастания:

727. Масса осколка Царь-колокола равна 11 500 кг. Масса Царь-колокола составляет 400/23 массы этого осколка. Найдите массу Царь-колокола.

728. Порция пельменей в кафе «Пампушечка» состоит из 18 пельменей. Иван Гурманов съедает за обедом 20/9 порции. Сколько пельменей съедает за обедом Иван? На сколько пельменей больше одой порции он съедает?

729. Найдите все натуральные значения х, при которых дробь х/9 будет правильной.

х=1, 2, 3, 4, 5, 6, 7, 8.

730. Найдите все натуральные значения х, при которых дробь х/15 будет правильной.

х=1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14.

731. Найдите все натуральные значения х, при которых дробь 6/х будет неправильной.

732. Найдите все натуральные значения х, при которых дробь 13/х будет неправильной.

х=1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13.

733. Найдите все натуральные значения , при которых выполняется неравенство:

734. Найдите все натуральные значения , при которых выполняется неравенство:

735. Какие цифры можно поставить вместо звездочки, чтобы:

736. Найдите все натуральные значения b, при которых дробь 3b+2/16 будет правильной.

737. Найдите все натуральные значения b, при которых дробь 42/10+4b будет неправильной.

738. Найдите все натуральные значения , при которых:

739. Найдите все натуральные значения , при которых:

УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ

740. Объем прямоугольного параллелепипеда равен 180 дм3, а два его измерения — 6 дм и 15 дм. Найдите сумму длин всех ребер параллелепипеда.

741. Из двух городов, расстояние между которыми равно 392 км, выехали одновременно навстречу друг другу два автомобиля. Скорость одного автомобиля равна 48 км/ч, что составляет 6/7 скорости второго. Какое расстояние будет между автомобилями через 5 ч после начала движения?

ЗАДАЧА ОТ МУДРОЙ СОВЫ

742. Мартышка, Удав, Слоненок и Попугай съели вместе 70 бананов, причем каждый из них съел хотя бы один банан. Мартышка съела больше, чем кто-либо из них, Попугай и Слоненок съели вместе 45 бананов. Сколько бананов съел Удав?

Источник: matem-gdz.ru