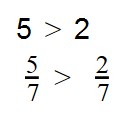Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.
Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.
Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются операциями отношения, такими как больше (>) или меньше (<).
Ученые-математики уже позаботились о готовых правилах, позволяющие сразу ответить на вопрос какая дробь больше, а какая меньше. Эти правила можно смело применять.
Мы рассмотрим все эти правила и попробуем разобраться, почему происходит именно так.
Сравнение дробей с одинаковыми знаменателями
Дроби, которые нужно сравнить, попадаются разные. Самый удачный случай это когда у дробей одинаковые знаменатели, но разные числители. В этом случае применяют следующее правило:
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше. И соответственно меньше будет та дробь, у которой числитель меньше.
Сравнение дробей, как узнать какая дробь больше, какая меньше.
Например, сравним дроби и и ответим какая из этих дробей больше. Здесь одинаковые знаменатели, но разные числители. У дроби числитель больше, чем у дроби . Значит дробь больше, чем . Так и отвечаем. Отвечать нужно с помощью значка больше ( > )
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. пиццы больше, чем пиццы:
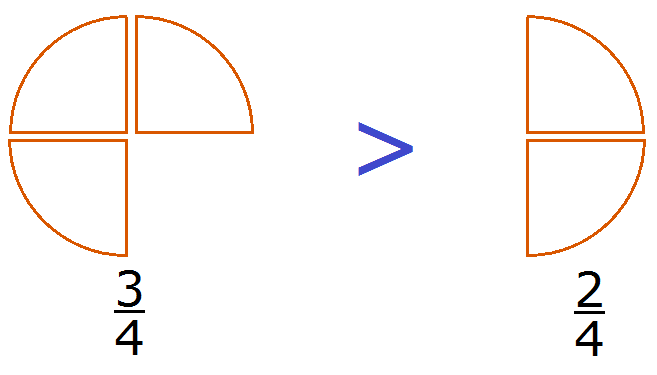
Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с одинаковыми числителями
Следующий случай это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.
Например, сравним дроби и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби . Значит дробь больше, чем дробь . Так и отвечаем:
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:

Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с разными числителями и разными знаменателями
Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями. Например, сравнить дроби и .
Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.
Приведём дроби и к одинаковому (общему) знаменателю. Найдём наименьшее общее кратное (НОК) знаменателей обеих дробей. НОК знаменателей дробей и это число 6.
Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:
Теперь найдём второй дополнительный множитель. Разделим НОК на знаменатель второй дроби . НОК это число 6, а знаменатель второй дроби это число 3. Делим 6 на 3, получаем дополнительный множитель 2. Записываем его над второй дробью:
Умножим дроби на свои дополнительные множители:
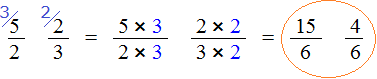
Мы пришли к тому что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:
Правило правилом, а мы попробуем разобраться почему больше, чем . Для этого выделим целую часть в неправильной дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.
После выделения целой части в дроби , получим следующее выражение:
Теперь можно легко понять, почему больше, чем . Давайте нарисуем эти дроби в виде пицц:
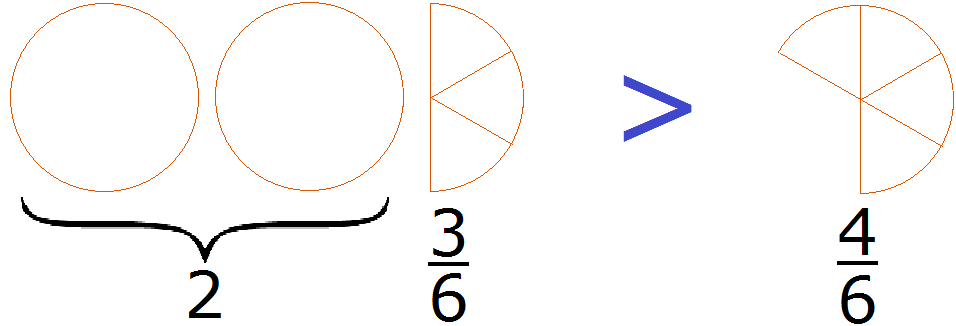
2 целые пиццы и пиццы, больше чем пиццы.
Вычитание смешанных чисел. Сложные случаи.
Вычитая смешанные числа иногда можно обнаружить, что всё идёт не так гладко как хотелось бы.
При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.
Например, 10 − 8 = 2
Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.
А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5 − 7 = −2
В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.
Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.
С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.
Например, решим пример .
Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. больше чем
поэтому смело можем вернуться к примеру и решить его:
Теперь решим такой пример
Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:
В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.
Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения .
Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать как это сделать. Если испытываете затруднения на этом моменте, обязательно изучите действия с дробями.
После приведения дробей к одинаковому знаменателю, получаем следующее выражение:
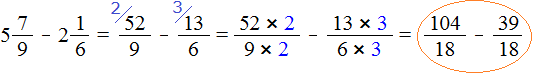
Теперь нужно сравнить дроби и . Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .
А это значит что уменьшаемое больше, чем вычитаемое
А значит мы можем вернуться к нашему примеру и смело решить его:
Пример 3. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю:
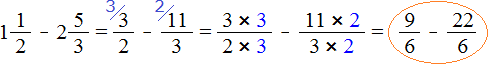
Теперь сравним дроби и . У дроби числитель меньше, чем у дроби , значит дробь меньше, чем дробь
А это значит, что и уменьшаемое меньше, чем вычитаемое
А это гарантировано приведёт нас в мир отрицательных чисел. Поэтому разумнее остановиться на этом месте и не продолжать вычисление. Продолжим его после изучения отрицательных чисел.
Пример 4. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем их к одинаковому (общему) знаменателю:
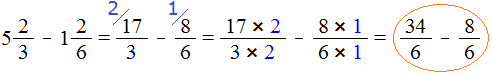
Теперь нужно сравнить дроби и . У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .
А это значит, что уменьшаемое больше, чем вычитаемое
Поэтому мы смело можем продолжить вычисление нашего примера:
Сначала мы получили ответ . Эту дробь мы сократили на 2 и получили дробь , но такой ответ нас тоже не устроил и мы выделили целую часть в этом ответе. В итоге получили ответ .
Источник: spacemath.xyz
Какая дробь самая большая?
Как известно, разница между знаменателем и числителем равна 1, тогда дробь с наибольшим числителем является наибольшей дробью. ∴ 7/8 является наибольшей дробью. Следовательно, 7/8 — самая большая дробь.
Аналогично, как найти наибольшую дробь?
Какая дробь больше 3 4 или 1 2? Ответ: Да, 3/4 больше 1/2.
Похожие страницы:Блог
Какие есть 3 вида налогов?
Как найти среднюю точку между двумя точками?
Как вы делаете кадровые прогнозы?
Как найти начальную скорость, зная только время?
Десятичная дробь 0.75 больше 0.5, поэтому 3/4 больше 1/2.
Какие дроби меньше 1 2? Отвечать. 16 дробей меньше половины. 1/9, 2/9, 3/9, 4/9, 1/8, 2/8, 3/8, 1/7, 2/7, 3/7, 1/6, 2/6, 1/ 5, 2/5, 1/4, 1/3.
Во-вторых Какая дробь больше 4 7 или 1 2? Преобразование в десятичное число
Теперь, когда эти дроби были преобразованы в десятичный формат, мы можем сравнить числа, чтобы получить наш ответ. 0.5714 больше 0.5, что также означает, что 4/7 больше 1/2.
Что больше половина или 2 3?
тогда Какие дроби больше 1 2? Если числитель больше половины знаменателя, то и дробь больше половины.) … Так как 4/6 больше 3/6, то 4/6 также больше 1/2.)
Какая дробь больше 1? Студенты, которые преуспели в этом, уже обобщили правило: дроби больше 1 имеют числители больше своих знаменателей; те, которые меньше единицы, имеют числители меньше, чем их знаменатели; остальные равны 1.
Какие дроби меньше 2 3?
Ответ: 4/6, 6/9, 8/12, 10/15 … Эквивалентны 2/3. Все дроби, полученные умножением числителя и знаменателя 2/3 на одно и то же число, эквивалентны 2/3. Все эквивалентные дроби сводятся к одной и той же дроби в простейшей форме.
Что больше ½ или ¼? Дробь 1/4 меньше чем 1/2 . Это может показаться странным, поскольку число 4 больше числа 2.
Какая дробь больше 2/3 или 5 6?
Это наименьшее число, которое можно разделить как на 6, так и на 3. В этом случае наименьший общий знаменатель равен 6. Теперь, когда эти дроби были преобразованы в один и тот же знаменатель, мы можем ясно видеть, глядя на числители, что 5 больше 4, что также означает, что 5/6 больше 2/3.
Какой из них больше 1 3 или 2 3? Как видите, знаменатель уже одинаков для обеих дробей, поэтому нам не нужно преобразовывать ни одну из дробей. Все, что нам нужно сделать, это посмотреть на числители над дробной чертой. Глядя на числители, мы ясно видим, что 2 НЕ меньше 1, что также означает, что 2/3 НЕ меньше 1/3.
Какая дробь больше 2/3 или 5 6?
Дробь 5/6 больше, чем 2/ 3.
Какая дробь больше 4 5 или 2 3?
Преобразование в десятичное
Теперь, когда эти дроби были преобразованы в десятичный формат, мы можем сравнить числа, чтобы получить наш ответ. 0.8 больше 0.6667, что также означает, что 4/5 больше 2/3.
Какая дробь меньше 1 3 или 2 3? Как видите, знаменатель уже одинаков для обеих дробей, поэтому нам не нужно преобразовывать ни одну из дробей. Все, что нам нужно сделать, это посмотреть на числители над дробной чертой. Глядя на числители, мы ясно видим, что 2 НЕ меньше 1, что также означает, что 2/3 НЕ менее 1/3.
Какие дроби равны 1? Мы также знаем, что когда вы у дроби одинаковые числитель и знаменатель, оно всегда равно 1. Например: Итак, пока мы умножаем или делим верхнюю и нижнюю часть дроби на одно и то же число, это точно так же, как умножение или деление на 1, и мы не изменим значение дробь.
Какая дробь больше 1 2 или 310?
Преобразование в десятичное
0.5 больше 0.3, что также означает, что 1/2 больше 3/10.
Как вы определяете дроби больше 1?
Сколько дробей от 0 до 1?
Сколько дробей лежит между 0 и 1? Решение: Между любыми двумя заданными числами бесконечное количество чисел. Следовательно, есть бесконечные дроби лежащие между 0 и 1.
Всегда ли дроби меньше 1? Самый простой тип дроби — это правильная дробь, которая всегда является лишь частью одного целого. В правильной дроби числитель всегда меньше знаменателя, а его значение всегда меньше 1.
Какая дробь больше 4 6 или 2 3?
Это наименьшее число, которое можно разделить как на 3, так и на 6. В этом случае наименьший общий знаменатель равен 6. Теперь, когда эти дроби были преобразованы в один и тот же знаменатель, мы можем ясно видеть, глядя на числители, что 4 НЕ больше 4, что также означает, что 2/3 НЕ больше, чем 4/6.
Какие дроби больше 2 3? 2/3 это то же самое, что 14/21 (я умножил на 7 сверху и снизу), а 3/7 равно 9/21 (я умножил на 3 сверху и снизу), поэтому 2/3 больше, чем 3/7, потому что 14/21 больше, чем 9/21. Затем мы можем сравнить 2/3 с 4/8.
Источник: reviews.tn
Что больше: три пятых или пять седьмых?
Можно и не приводить к общему знаменателю.Пояснени е.Рассмотрим дроби в которых разница между знаменателем и числителем одна и та же.Для определённости числитель меньше знаменателя.Дроби правильные ,положительные.Напри мер 12; 23 ;34 ; 45 и так далее.Здесь разница между знаменателем и числителем=1.То есть 2-1=3-2=4-3=. =1 и видно что 12<23<34<. В нашем случае разница=2.И 13<24<35<46<57. ..То есть 35 <57.Даже можно вывести правило : Из двух обыкновенных правильных положительных дробей при одинаковой разнице между числителем и знаменателем больше та дробь у которой знаменатель больше.
система выбрала этот ответ лучшим
комментировать
в избранное ссылка отблагодарить
Augus tine [5.4K]
4 года назад
Посчитать просто — приводим дробь к общему знаменателю, т.е. 5х7 = 35.
В первой дроби 3х7 в числителе, во второй — 5х5. Выходит 21 и 25. Соответственно, 5/7 (25/35) больше, чем 3/5 (21/35). Конечно, это верно для нашей привычной системы счисления.
Сомневаетесь в определении на глаз — считайте.
комментировать
в избранное ссылка отблагодарить
tana7 6 [123K]
4 года назад
Это правило математики на сравнение обыкновенных дробей: для того,чтобы их сравнить, нужно, чтобы они были сопоставимы — то есть они должны иметь одинаковый знаменатель.
Общим знаменателем для этих дробей будет знаменатель 35 — число, на которое делится и знаменатель первой дроби 5, и знаменатель второй дроби 7.
В первой дроби числитель и знаменатель умножаем на 7 — получаем дробь 21/35.
Во второй дроби числитель и знаменатель умножаем на 5 — получаем дробь 25/35.
Теперь видно, что вторая дробь (5/7) больше.
Источник: www.bolshoyvopros.ru
Сравнение дробей: как правильно
Все познается в сравнении и особенно — дроби. Давайте узнаем, как и когда сравнивать дроби и чем это может быть полезно в жизни.
17 декабря 2020
· Обновлено 28 октября 2022
Сравнение дробей с одинаковыми знаменателями
Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.
Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:
Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.
А теперь на примерах.
Пример 1. Сравните дроби:
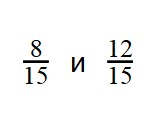
- Мы видим, что знаменатели дробей — равны. Значит сравниваем числители:
8 < 12
12 > 8 - Это значит, что
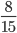 <
< 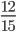 Изи!
Изи!
Пример 2. Сравните дроби:
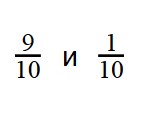
- Как и в прошлом примере, знаменатели дробей — равны. Сравниваем числители:
9 > 10
1 < 10 - Это значит, что
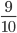 >
>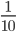
Пример 3. Сравните дроби:
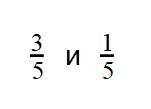
- Знаменатели дробей снова равны. Сравниваем числители:
3 > 1
1 < 3 - Это значит, что
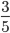 >
>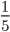
Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший числитель.
Давайте разберем наглядный пример сравнения дробей. Еще больше наглядных примеров — на курсах по математике в онлайн-школе Skysmart!

Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
- Запишем в виде дробей:
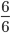 и
и 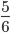
- А теперь сравним полученные дроби: знаменатели — равны, сравниваем числители:
6 > 5
5 < 6. - Это значит, что
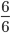 >
>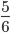
Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Пройти урок

Сравнение дробей с одинаковыми числителями
Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.
Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.
А теперь наши любимые примеры. Погнали!
Пример 1. Сравните дроби:
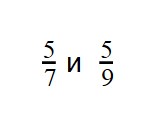
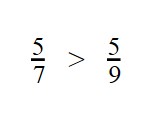
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
9 > 7
7 < 9 - Значит, дробь с меньшим знаменателем — больше:
Пример 2. Сравните дроби:
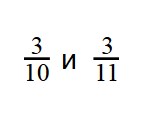
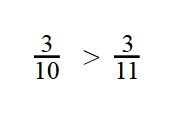
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
10 < 11
11 > 10 - Значит дробь с меньшим знаменателем — больше:
Пример 3. Сравните дроби:
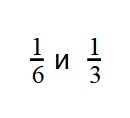
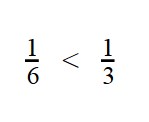
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
6 > 3
3 < 6 - Значит, дробь с меньшим знаменателем — больше.
Для наглядности представим ситуацию, в которой вам предстоит разделить торт между тремя друзьями. Это значит, что 6 кусков торта равномерно распределяются по 3 людям: каждому достается 6:3 = 2 по 2 кусочка.
А теперь представим более приятную ситуацию: кусков торта по-прежнему 6, а друзей уже только 2. Тогда каждому достанется по 3 вкуснейших кусочка:
Как видите, сравнение дробей может вам пригодиться в самых неожиданных ситуациях. Теперь, когда снова придется хорошенько задуматься о соотношении кусков торта и приглашенных гостях, изученная тема поможет вам принять верное решение.
Сравнение дробей с разными числителями и разными знаменателями
Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.
Запоминаем
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю, а затем сравнить числители.
Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.
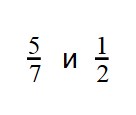
- Нужно подобрать число, которое будет делиться на 7 и на 2, например, 14. Проверим:
14:7 = 2
14 : 2 = 7 - Первую дробь умножаем на дополнительный множитель 2:
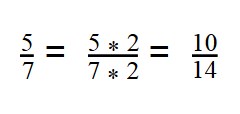
- Вторую дробь умножаем на дополнительный множитель 7:
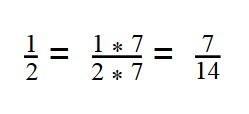
- Дроби приведены к общему знаменателю:
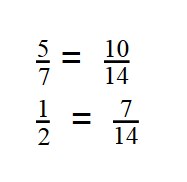
Давайте потренируемся в сравнении дробей.
Пример 1. Сравните дроби:
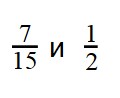
- Приведем дроби к общему знаменателю. 30 делится на 15 и на 2.
30 : 15 = 2
30 : 2 = 15 - Первую дробь умножаем на дополнительный множитель 2:
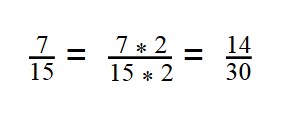
- Вторую дробь умножаем на дополнительный множитель 15:
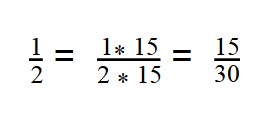
- Дроби приведены к общему знаменателю:
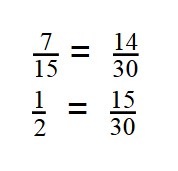
- Если две дроби имеют одинаковые знаменатели, то, согласно правилу, больше та дробь, чей числитель больше:
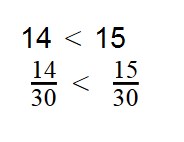
При сравнении неправильных дробей с правильными помните, что неправильная дробь всегда больше правильной.
Пример 2: Сравните дроби:
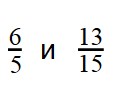
- 6/5 — неправильная дробь.
- Выделим целую часть:
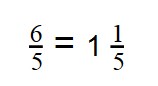
- Значит, что
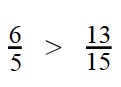
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Записаться на интенсив

Вычитание смешанных чисел
Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.
- 12 — 7 = 6
12 — уменьшаемое
7 — вычитаемое
5 — разность
В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».
При вычитании дробей действует тот же самый принцип: вычитаемое должно быть меньше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
Пример 1. Вычислите:
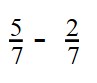
Вычитаемая дробь меньше уменьшаемой
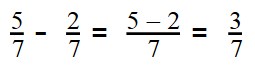
- Выполняем вычитание:
Пример 2.Найдите разность:
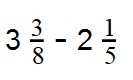
- Смешанные дроби превращаем в неправильные:
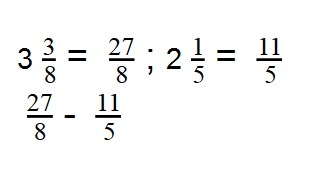
- Чтобы найти разность дробей с разными числителями и знаменателями, нужно привести их к общему знаменателю:
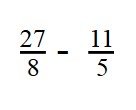
- Наименьшее общее кратное — 40
40 : 8 = 5
40 : 5 = 8 - Умножаем первую дробь на дополнительный множитель 5:
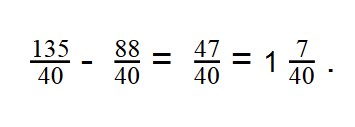
- Умножаем вторую дробь на дополнительный множитель 8:
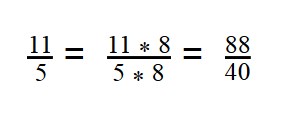
- Дроби приведены к общему знаменателю:
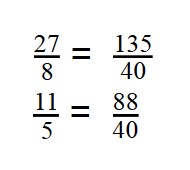
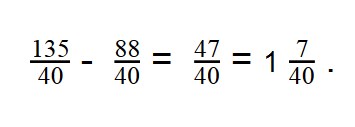
Примеры для самопроверки
Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.
Пример 1. Сравните дроби:
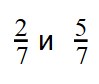
Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что
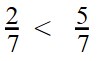
Пример 2. Сравните дроби:
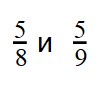
Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что
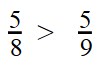
Пример 3. Сравните дроби:
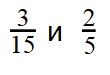
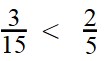
Ответ:.
- По правилу сравнения дробей с разными числителями и знаменателями, сначала нужно привести дроби к общему знаменателю:
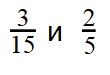
- Наименьшее общее кратное — 15:
15 : 15 = 1
15 : 5 = 3 - Умножаем первую дробь на дополнительный множитель 1:
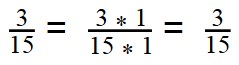
- Умножаем вторую дробь на дополнительный множитель 3:
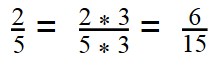
- Дроби приведены к общему знаменателю:
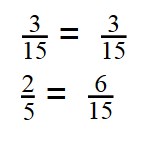
- Сравниваем числители получившихся дробей: 3 < 6
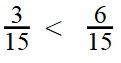
Пример 4. Найдите разность:
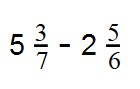
- Смешанные дроби превращаем в неправильные:
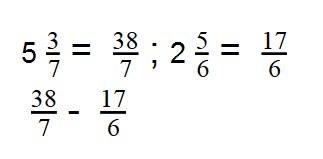
- Чтобы найти разность дробей с разными числителями и знаменателями, нужно привести их к общему знаменателю.
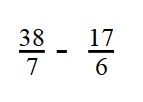
- Наименьшее общее кратное — 42:
42 : 7 = 6
42 : 6 = 7 - Умножаем первую дробь на дополнительный множитель 6:
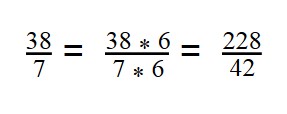
- Умножаем вторую дробь на дополнительный множитель 7:
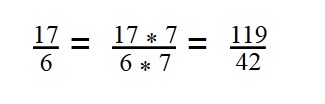
- Дроби приведены к общему знаменателю.
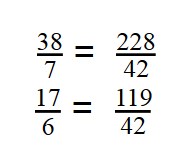
- Теперь можно вычитать:
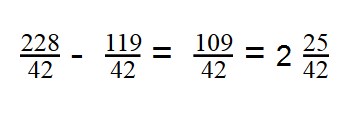
Источник: skysmart.ru
Сравнение дробей

Когда дело доходит до дробей, мы обычно сравниваем две или более. На самом деле, мы сталкиваемся с дробями в нашей повседневной жизни. Простой пример: если вы разрезаете яблоко на две части, оно тоже будет дробью. В принципе, сравнение двух дробей означает определение большей и меньшей части среди них.
Понятие сравнения дробей
Определение
Дробь – это число, представляющее часть целого. Это целое может быть одним объектом или группой объектов. Дробь записывается как [frac
] , где p и q являются целыми числами и q≠0.
Такие числа, как [frac, frac, frac, frac] известны как дроби.
Число под линией деления называется знаменателем. Оно описывает нам, на сколько равных частей делится целое. Число над строкой называется числителем. Оно говорит нам, сколько равных частей взято.
Пример: [frac, frac, frac] и т.д. являются дробями.
Сравнить две дроби – это значит понять, какая из них больше, а какая меньше. Из двух дробей с равными знаменателями больше будет та, у которой числитель больше, и меньше та, у которой числитель меньше. Примеры сравнения дробей в реальном времени включают различные действия, такие как проверка сниженных цен во время покупок, достижение продаж определенного продукта, медицинские рецепты врача, результаты тестов и экзаменов и т.д. Опять же, сравнение дробей – это то, что мы испытываем или с чем сталкиваемся в своей повседневной жизни. Если достаточно сосредоточиться, то можно легко получить практическое представление об одном и том же каждый день, выполняя обычные домашние дела и математические вычисления.
Правила сравнения дробей
Есть несколько правил, которым мы должны следовать при сравнении дробей:
- Когда знаменатели дроби одинаковы, дробь с меньшим числителем является меньшей дробью, а дробь с большим числителем считается большей дробью.
- Когда числители равны, дроби считаются эквивалентными.
- Когда дроби имеют один и тот же числитель, чем меньше числитель, тем более значимой считается дробь.
Сравнение дробей с одинаковыми знаменателями
Определение
Подобные дроби — это две или более фракции, имеющие один и тот же знаменатель.
Пример: [frac, frac, frac] являются «подобными дробям».
Сравнение подобных дробей
В этом методе необходимо проверить, совпадают ли знаменатели или нет. Если знаменатели одинаковы, то дробь с большим числителем является более значительной дробью. Дробь с меньшим числителем – это меньшая дробь. Если и числители, и знаменатели равны, то дроби также идентичны. Пример: Давайте сравним [frac] и [frac].
- Найдем знаменатели данных дробей: [frac] и [frac]. Здесь знаменатели одинаковы.
- Сравним числители: 16>6.
- Теперь дробь с большим числителем будет больше.
- Следовательно, [frac] и [frac].
Сравнение дробей с разными знаменателями
Определение
Неподобные дроби — это две или более дроби имеющие разные знаменатели.
Пример: [frac] и [frac] являются неподобными дробями.
Сравнение неподобных дробей
Чтобы сравнить дроби с разными знаменателями, следует начать с поиска наименьшего общего знаменателя, чтобы сделать их значения одинаковыми. Когда знаменатели преобразуются в одни и те же знаменатели, то дробь с большим числителем является более значимой — например, [frac] и [frac].
- Найдите знаменатели данных дробей: [frac] и [frac], здесь знаменатели не совпадают. Возьмем 2 и 5 так, что общий множитель равен 10. Здесь, [frac=fractimes fractext frac=fractimes frac].
- Теперь сравним доли,[frac] и [frac], знаменатели одинаковы.
- Мы сравним числители, 5 > 4.
- Сравнение дроби, [frac] > [frac]. Дробь с большим числителем является большей дробью.
- Таким образом, [frac] > [frac]. Поэтому, [frac] > [frac]
Если знаменатели разные, а числители одинаковые, то можно легко сравнить дроби, посмотрев на их знаменатели. Дробь с меньшим знаменателем имеет большее значение. Дробь с большим знаменателем имеет меньшее значение.
Десятичный метод сравнения дробей
В этом методе необходимо сравнить десятичные значения дробей. Сначала числитель делится на знаменатель, а затем дробь преобразуется в десятичную дробь. Затем сравниваются десятичные значения.
- Сначала запишем заданные дроби [fracи frac] в десятичной форме. [frac]= 0,8 и [frac]= 0,75.
- Теперь сравните десятичные значения, 0,8 > 0,75.
- Здесь дробь с большим десятичным значением является большей дробью.
- Следовательно, [fracи frac].
Сравнение дробей с помощью перекрестного умножения
В этом методе числитель одной дроби перекрестно умножается на знаменатель другой дроби.
Пример: [frac text < и >frac], когда мы перекрестно умножаем, мы получаем 1×4=4 и 2×3=6.
- Теперь цифры 4 и 6 являются числителями, которые мы получаем, если выразим [fractext < и >frac] с общим знаменателем 8.
- Далее, новые дроби с одинаковыми знаменателями будут равны [fractext < и >frac].
- Итак, число 6 является большим числителем, [frac< frac].
- Следовательно, [frac< frac].
Нет времени решать самому?
Источник: www.napishem.ru