Чтобы освоить умножение многозначных чисел, нужно всего лишь знать таблицу умножения и уметь складывать числа. В сущности, вся сложность заключается в том, как правильно разместить промежуточные результаты умножения (частичные произведения). Стремясь облегчить вычисления, люди придумали множество способов умножения чисел. За многовековую историю математики их набралось несколько десятков.
Умножение способом решётки. Иллюстрация из первой печатной книги по арифметике. 1487 год.
Палочки Непера. Этот простой счётный прибор впервые был описан в сочинении Джона Непера «Рабдология». 1617 год.
Джон Непер (1550—1617).
Модель счётной машины Шиккарда. Это не дошедшее до нас вычислительное устройство изготовлено изобретателем в 1623 году и описано им годом позже в письме Иоганну Кеплеру.
Вильгельм Шиккард (1592—1635).
Наследие индусов — способ решётки
Индусы, с давних времён знавшие десятичную систему счисления, предпочитали устный счёт письменному. Они изобрели несколько способов быстрого умножения. Позже их заимствовали арабы, а от них эти способы перешли к европейцам. Те, однако, ими не ограничились и разработали новые, в частности тот, что изучается в школе, — умножение столбиком.
Палочки Непера и умножение решеткой.
Этот способ известен с начала XV века, в следующем столетии он прочно вошёл в употребление у математиков, а сегодня им пользуются повсеместно. Но является ли умножение столбиком лучшим способом осуществления этого арифметического действия? На самом деле существуют и другие, в наше время забытые способы умножения, ничуть не хуже, например способ решётки.
Этим способом пользовались ещё в древности, в Средние века он широко распространился на Востоке, а в эпоху Возрождения — в Европе. Способ решётки именовали также индийским, мусульманским или «умножением в клеточку». А в Италии его называли «джелозия», или «решётчатое умножение» (gelosia в переводе с итальянского — «жалюзи», «решётчатые ставни»). Действительно, получавшиеся при умножении фигуры из чисел имели сходство со ставнями-жалюзи, которые закрывали от солнца окна венецианских домов.
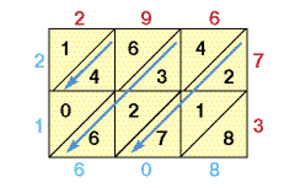
Суть этого нехитрого способа умножения поясним на примере: вычислим произведение 296 × 73. Начнём с того, что нарисуем таблицу с квадратными клетками, в которой будет три столбца и две строки, — по количеству цифр в множителях. Разделим клетки пополам по диагонали. Над таблицей запишем число 296, а с правой стороны вертикально — число 73.
Перемножим каждую цифру первого числа с каждой цифрой второго и запишем произведения в соответствующие клетки, располагая десятки над диагональю, а единицы под ней. Цифры искомого произведения получим сложением цифр в косых полосах. При этом будем двигаться по часовой стрелке, начиная с правой нижней клетки: 8, 2 + 1 + 7 и т.д. Запишем результаты под таблицей, а также слева от неё. (Если при сложении получится двузначная сумма, укажем только единицы, а десятки прибавим к сумме цифр из следующей полосы.) Ответ: 21 608. Итак, 296 x 73 = 21 608.
Палочки Непера
Способ решётки ни в чём не уступает умножению столбиком. Он даже проще и надёжнее, при том, что количество выполняемых действий в обоих случаях одинаково. Во-первых, работать приходится только с однозначными и двузначными числами, а ими легко оперировать в уме. Во-вторых, не требуется запоминать промежуточные результаты и следить за тем, в каком порядке их записывать.
Память разгружается, а внимание сохраняется, поэтому вероятность ошибки уменьшается. К тому же способ решётки позволяет быстрее получить результат. Освоив его, вы сможете убедиться в этом сами.
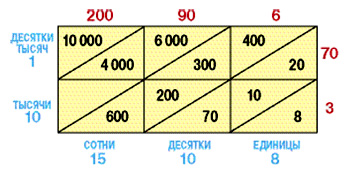
Почему способ решётки приводит к правильному ответу? В чём заключается его «механизм»? Разберёмся в этом с помощью таблицы, построенной аналогично первой, только в этом случае множители представлены как суммы 200 + 90 + 6 и 70 + 3.
Как видим, в первой косой полосе стоят единицы, во второй — десятки, в третьей — сотни и т.д. При сложении они дают в ответе соответственно число единиц, десятков, сотен и т.д. Дальнейшее очевидно:
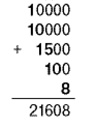
Иначе говоря, в соответствии с законами арифметики произведение чисел 296 и 73 вычисляется так:
296 x 73 = (200 + 90 + 6) x (70 + 3) = 14 000 + 6300 + 420 + 600 + 270 + 18 = 10 000 + (4000 + 6000) + (300 + 400 + 600 + 200) + (70 + 20 + 10) + 8 = 21 608.
Палочки Непера
Умножение способом решётки лежит в основе простого и оригинального счётного прибора — палочек Непера. Его изобретатель Джон Непер, шотландский барон и любитель математики, наряду с профессионалами занимался усовершенствованием средств и методов вычисления. В истории науки он известен, прежде всего, как один из создателей логарифмов.
Прибор состоит из десяти линеек, на которых размещена таблица умножения. В каждой клетке, разделённой диагональю, записано произведение двух однозначных чисел от 1 до 9: в верхней части указано число десятков, в нижней — число единиц. Одна линейка (левая) неподвижна, остальные можно переставлять с места на место, выкладывая нужную числовую комбинацию. При помощи палочек Непера легко умножать многозначные числа, сводя эту операцию к сложению.
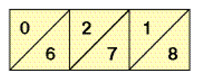
Например, чтобы вычислить произведение чисел 296 и 73, нужно умножить 296 на 3 и на 70 (сначала на 7, затем на 10) и сложить полученные числа. Приложим к неподвижной линейке три другие — с цифрами 2, 9 и 6 наверху (они должны образовать число 296). Теперь заглянем в третью строку (номера строк указаны на крайней линейке). Цифры в ней образуют уже знакомый нам набор.
Складывая их, как в способе решётки, получим 296 x 3 = 888. Аналогично, рассмотрев седьмую строку, найдём, что 296 x 7 = 2072, тогда 296 x 70 = 20 720. Таким образом,
296 x 73 = 20 720 + 888 = 21 608.
Палочки Непера применялись и для более сложных операций — деления и извлечения квадратного корня. Этот счётный прибор не раз пытались усовершенствовать и сделать более удобным и эффективным в работе. Ведь в ряде случаев для умножения чисел, например с повторяющимися цифрами, нужны были несколько комплектов палочек. Но такая проблема решалась заменой линеек вращающимися цилиндрами с нанесённой на поверхность каждого из них таблицей умножения в том же виде, как её представил Непер. Вместо одного набора палочек получалось сразу девять.
Подобные ухищрения в самом деле ускоряли и облегчали расчёты, однако не затрагивали главный принцип работы прибора Непера. Так способ решётки обрел вторую жизнь, продлившуюся ещё несколько столетий.
Машина Шиккарда
Учёные давно задумывались над тем, как переложить непростую вычислительную работу на механические устройства. Первые успешные шаги в создании счётных машин удалось осуществить только в XVII столетии. Считается, что раньше других подобный механизм изготовил немецкий математик и астроном Вильгельм Шиккард.
Но по иронии судьбы об этом знал лишь узкий круг лиц, и столь полезное изобретение более 300 лет не было известно миру. Поэтому оно никак не повлияло на последующее развитие вычислительных средств. Описание и эскизы машины Шиккарда были обнаружены всего полвека назад в архиве Иоганна Кеплера, а чуть позже по сохранившимся документам была создана её действующая модель.
По сути, машина Шиккарда представляет собой шестиразрядный механический калькулятор, выполняющий сложение, вычитание, умножение и деление чисел. В ней три части: множительное устройство, суммирующее устройство и механизм для сохранения промежуточных результатов. Основой для первого послужили, как нетрудно догадаться, палочки Непера, свёрнутые в цилиндры. Они крепились на шести вертикальных осях и поворачивались с помощью специальных ручек, расположенных наверху машины. Перед цилиндрами располагалась панель с девятью рядами окошек по шесть штук в каждом, которые открывались и закрывались боковыми задвижками, когда требовалось увидеть нужные цифры и скрыть остальные.
В работе счётная машина Шиккарда очень проста. Чтобы узнать, чему равно произведение 296 x 73, нужно установить цилиндры в положение, при котором в верхнем ряду окошек появится первый множитель: 000296. Произведение 296 x 3 получим, открыв окошки третьего ряда и просуммировав увиденные цифры, как в способе решётки. Точно так же, открыв окошки седьмого ряда, получим произведение 296 x 7, к которому припишем справа 0. Остаётся только сложить найденные числа на суммирующем устройстве.
Придуманный некогда индусами быстрый и надёжный способ умножения многозначных чисел, много веков применявшийся при расчётах, ныне, увы, забыт. А ведь он мог бы выручить нас и сегодня, если бы под рукой не оказалось столь привычного всем калькулятора.
Источник: www.nkj.ru
Индивидуальный проект по информатике «Палочки Джона Непера»

1. Индивидуальный проект по Информатике «Палочки Джона непера»
Государственное профессиональное образовательное учреждение
Тульской области «Тульский педагогический колледж»
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
ПО ИНФОРМАТИКЕ
«ПАЛОЧКИ ДЖОНА НЕПЕРА»
Выполнила:
Студентка 1 курса ДС группы,
Специальность «Коррекционное
Дошкольное воспитание»
Азарова Мирослава
2018
Проверил:
Учитель информатики
Корогодина Алёна Игоревна
2. Введение
ВВЕДЕНИЕ
В наше время одним из важных компонентов является
вычислительная техника, так как мы очень часто
нуждаемся в различных вычислениях. Человек всегда
нуждался в счёте и нуждается в нём до сих пор. Раньше, до
появления различных вычислительных приборов, люди
считали на пальцах, веточками, узлами, которые
располагали в определённой последовательности. Но
время шло и мир развивался, а с ним развивалась и
вычислительная техника.
3. введение
ВВЕДЕНИЕ
Так появились новые способы вычислений и нам
стало интересно, а как же зарождались
различные способы вычислений, и как люди ими
пользовались.
В частности нам стало интересно и появление
такого вычислительного прибора, как палочки
Джона Непера.
Актуальность данной работы можно определить
по интересам к развитию вычислительной
техники, способам вычисления , как же всё таки
появились палочки Джона Непера и способ их
применения. Таким образом у нас зарождается
идея темы для данного проекта.
4. введение
ВВЕДЕНИЕ
Объект исследования: история развития вычислительной
техники.
Предмет исследования: палочки Джона Непера.
Цель работы: создание палочек Джона Непера.
Задачи:
Изучить историю развития вычислительной техники
домеханической эпохи.
Рассмотреть разновидности счётных палочек Джона Непера.
Создать палочки Джона Непера.
Практическая значимость работы заключается в том, чтобы
было
возможным
использование
вычислительного
приробора на уроках информатики и ИКТ.
5. период развития
ПЕРИОД РАЗВИТИЯ
Развитие вычислительной техники (ВТ) принято делить
на следующие этапы:
1. Электронный ( с 40-х годов XX века)
2. Ручной( домеханический, 50 тыс. лет до н.э.)
3. Механический (начало XVII века)
4. Электромеханический (с 90-х годов XIX века)
6. Домеханический период
ДОМЕХАНИЧЕСКИЙ ПЕРИОД
Ручной период автоматизации вычислений начался
еще на заре человеческой цивилизации и
базировался на использовании частей тела, в первую
очередь пальцев рук и ног. Далее стали появляться
другие вспомогательные средства счета: палочки,
узелки, насечки и т. п.
7. Домеханический период
ДОМЕХАНИЧЕСКИЙ ПЕРИОД
Чтобы сделать процесс счета более удобным,
первобытный человек начал использовать вместо
пальцев небольшие камни.
С развитием государств Европы и Азии были
изобретены
новые
способы
вычислений:
деревянные или каменные бороздки с песком
или
камнями,
абак,
счёты,
палочки,
логарифмическая линейка и многие другие.
8. Домеханический период
ДОМЕХАНИЧЕСКИЙ ПЕРИОД
9. Палочки Джона Непера
ПАЛОЧКИ ДЖОНА НЕПЕРА
Счетные палочки – это изобретение шотландского
математика Джона Непера, который вошел в
историю, благодаря изобретению логарифмов. С
помощью первой вычислительной техники развитие
арифметики сделало шаг вперед, а «палочки
Непера» до сих пор считаются прообразом первой
вычислительной техники, например, такой, как
калькулятор.
10. Палочки джона непера
ПАЛОЧКИ ДЖОНА НЕПЕРА
«Палочки Непера» представляли собой комплект
специальных палочек, состоящих из дощечки с
разметкой от одного до девяти и остальными
палочками, на которые была помещена таблица
умножения с такой же разметкой цифр. Вверху
каждой дощечки располагались числа в порядке
возрастания, а по всей длине выложенной таблицы
Непер разместил собственно результаты умножения
чисел на цифры от одного до девяти. Иными
словами, таблица давала возможность совершать
операции умножения числа 123456789 на число
123456789. Сама сетка была разделена столбцами.
11. Палочки джона непера
ПАЛОЧКИ ДЖОНА НЕПЕРА
12. Палочки джона непера
ПАЛОЧКИ ДЖОНА НЕПЕРА
«Палочки Непера» могли использоваться, как для
операции умножения, так и для деления, и
вычисления квадратного корня числа.
После изобретения этого арифметического метода,
многие ученые-математики старались внести какието новшества в разработанный до них механизм.
«Палочки Непера» пользовались большим спросом в
свое время. Это, казалось бы, несложное открытие
сделало большой прорыв в области развития
арифметики.
13. Разновидности счётных приборов
РАЗНОВИДНОСТИ СЧЁТНЫХ
ПРИБОРОВ
Перед изобретением палочек Джона Непера, люди
пользовались другим вычислительным прибором,
как Абак. Абак — это счётная доска, применявшаяся
для арифметических вычислений приблизительно с
V века до н.э. В Древней Греции, Древнем Риме и в
Китае.
14. Абак (счёты)
АБАК (СЧЁТЫ)
В своей примитивной форме абак представлял собой
дощечку (позднее он принял вид доски,
разделенной на колонки перегородками). На ней
проводились линии, разделявшие ее на колонки, а
камешки раскладывались в эти колонки по тому же
позиционному принципу, по которому кладется
число на наши счеты.
15. Логарифмическая линейка
ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА
После изобретения палочек Джона Непера, была
создана Логарифмическая линейка
Прямоугольная логарифмическая линейка — это
счетный инструмент для упрощения вычислений, с
помощью которого операции над числами
заменяются операциями над логарифмами этих
чисел.
16. Логарифмическая линейка
ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА
Вычисления с помощью логарифмической линейки
производятся просто, быстро, но приближенно. И,
следовательно, она не годится для точных, например
финансовых, расчетов.
Прообразом счетного устройства была шкала для
вычислений английского математика Э. Гантера.
Шкала использовалась в сочетании с циркулем. Им
отмеривались
необходимые
градуированные
отрезки, которые потом складывались или
вычитались. Операции с числами заменялись
действиями с логарифмами. Используя их основные
свойства, умножить, делить, возводить в степень или
вычислять корень числа оказалось намного проще.
17. Умножение на палочках Непера
УМНОЖЕНИЕ НА ПАЛОЧКАХ НЕПЕРА
Прибор представлял собой набор прямоугольных
пластин (палочек), в который входили:
–палочки с результатами умножения всех чисел от 0
до 9 на числа от 0 до 9; сверху каждой палочки
наносилось число от 0 до 9 (на рис. 1 справа
показаны девять таких палочек). Результат
умножения на палочках представлен двумя цифрами
(в том числе начальным нулем), разделенными
наклонной чертой;
–одна палочка с нанесенными на нее цифрами от 1
до 9 (указатель строк); на рис. 1 она изображена
слева
18. Умножение на палочках непера
УМНОЖЕНИЕ НА ПАЛОЧКАХ НЕПЕРА
Рис.1
19. Умножение на палочках непера
УМНОЖЕНИЕ НА ПАЛОЧКАХ НЕПЕРА
Для умножения с помощью этого прибора
выбирались палочки, соответствующие значениям
разряда множимого, и выкладывались в ряд так,
чтобы цифры сверху каждой палочки составляли
множимое. На рис. 2 показан пример умножения
для числа 4938.
Слева прикладывали палочку —указатель строк, по
которой
выбирали
строки,
соответствующие
разрядам множителя. Для умножения, например, на
3, рассматривались соответствующие строки на
палочках с цифрами 4, 9, 3 и 8.
20. Умножение на палочках непера
УМНОЖЕНИЕ НА ПАЛОЧКАХ НЕПЕРА
Рис.2
21. Умножение на палочках непера
УМНОЖЕНИЕ НА ПАЛОЧКАХ НЕПЕРА
Результат умножения определялся следующим
образом:
–последняя цифра произведения равна 4 (цифра под
чертой в крайней справа палочке);
–остальные цифры определялись суммированием
цифр «по наклонной линии: предпоследняя цифра
равна 1 (2 + 9 = 11, единица переходит в старший
разряд), следующая справа цифра —8 (0 + 7, иеще 1
перешло справа), следующая —4 (2 + 2), первая
слева —1. Итак, результат равен 14814.
22. Умножение на палочках непера
УМНОЖЕНИЕ НА ПАЛОЧКАХ НЕПЕРА
Если множитель являлся многозначным, то
результаты, полученные для каждой строки (для
каждой цифры множителя),складывались между
собой с учетом порядка разрядов.
23. Изготовление палочек непера
ИЗГОТОВЛЕНИЕ ПАЛОЧЕК НЕПЕРА
Для их создания нам понадобится:
Лист фанеры размером 60 на 40 см и толщиной 7
мм
Линейка
Лобзик
Кисточка
Лаковое покрытие для дерева
Выжигательный прибор
Карандаш
24. Изготовление палочек непера
ИЗГОТОВЛЕНИЕ ПАЛОЧЕК НЕПЕРА
Взять лист фанеры и разлиновать его.(см. Рис. 3)
Рис.3
25. Изготовление палочек непера
ИЗГОТОВЛЕНИЕ ПАЛОЧЕК НЕПЕРА
Распилить лобзиком лист фанеры на 10 частей, чтобы
получились палочки(см.рис 4)
После с помощью шлифовальной бумаги зачистить
края палочек.
Затем наноситься лаковое покрытие.(см.рис.5)
Рис.4
Рис.5
26. Изготовление палочек непера
ИЗГОТОВЛЕНИЕ ПАЛОЧЕК НЕПЕРА
После дожидаемся, когда высохнет лак. И наносим
цифровую разметку следуя примеру из интернета
(см.рис.6), которую потом будем выжигать.(см.рис.7)
Рис.6
Рис.7
27. Изготовление палочек непера
ИЗГОТОВЛЕНИЕ ПАЛОЧЕК НЕПЕРА
После того, как была нанесена разметка, мы с помощью
выжигательного прибора, выжигаем все цифры. И в
результате мы получаем итог работы(см. рис. 8 и 9)
Рис.8
Рис.9
28. Заключение
ЗАКЛЮЧЕНИЕ
Палочки Джона Непера прослужили довольно долгое
время людям, помогая им с вычислениями. Но время
шло и изобретались новые вычислительные приборы,
поэтому палочки остались в прошлом и уже не
применяются. К сожалению нынешние приборы хоть и
помогают быстрее вычислять, они не помогают нам
развиваться и производить какие-либо расчёты в уме,
как это было с домеханическими вычислительными
приборами. Поэтому хоть и произошёл скачёк в развитии
вычислительной техники, но лучшими приборами всё
равно останутся приборы домеханической эпохи, так как
они помогали нам развиваться.
Источник: ppt-online.org
Палочки Непера — удивительный счётный прибор из 16 века. Сделал и показываю, как работает
Приветствую Вас, уважаемые Читатели! Сегодня я хочу рассказать Вам об устройстве для счета, которое придумал изобретатель логарифмов и шотландский лорд Джон Непер.

Палочки Непера позволяют умножать числа, вплоть до десятизначных, на любые однозначные. Не густо, конечно, но вспомните, какой шел век! Уже и такая автоматизация была интересной.



Понравилась статья? Поделиться с друзьями:
Вам также может быть интересно
История математики 0
Сегодня мой рассказ будет строиться на основе выпуска замечательного журнала «Математика в школе №
Математические лайфхаки 0
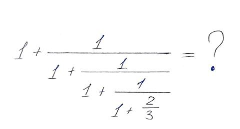
В начале способ кажется абсолютной магией, доступной «не только лишь всем», но потом становится
Математические лайфхаки 0
Приветствую Вас, уважаемые Читатели! Предлагаю Вам решить арифметическую задачку, которая, на первый взгляд, выглядит
Научно-популярная математика 0
Приветствую Вас, уважаемые Читатели! Скорее всего подписчиков канала «Математика не для всех» не найдется
Красота математики 0
Приветствую Вас, уважаемые Читатели! Мир геометрических теорем полон красоты. Вот и сегодня я расскажу
История математики 0
Приветствую Вас, уважаемые Читатели! Все мы привыкли к четкому разделению: в математике мы используем
Источник: xn——5cdaaroede2a0atecw2fed0f9k.xn--p1ai
6 инструментов Политеха, чтобы понять математику
Нередко у школьников вызывают затруднения такие задачи, как деление угла на части при помощи циркуля и линейки, вычисление суммы внутренних углов или же соединение точек в идеальную параболу. «Мел» вместе с преподавателями Лаборатории математики Политеха рассказывает о наглядных инструментах, которые помогают детям через игру глубже понять некоторые математические факты.

1. Трисектор на антипараллелограммах

Кому будет полезно. 7-11 классы.
Какие темы поможет понять. Свойства параллелограмма и пространственного четырехугольника с противоположными сторонами; подобие фигур.
Описание. Одна из древнейших и неразрешимых задач — деление произвольного угла на три части циркулем и линейкой. А решить ее можно при помощи этого инструмента — трисектора, составленного из трех антипараллелограммов. Антипараллелограмм — четырехугольник с равными, но непараллельными противоположными сторонами.
Присутствующие здесь три остаются подобными при движении механизма. Доказательство этого утверждения представляет неплохую задачу для девятиклассников.
Трисектор используется в Лаборатории математики Политеха на школьных занятиях «Некоторые формулы геометрии» для 7-8-х классов и «Плоские шарнирные механизмы» для 7-11-х классов.
2. Счетные палочки Непера

Кому будет полезно. 1-3 классы.
Какие темы помогут понять. Устный счет, таблица умножения, наглядное умножение в столбик, устройство механических калькуляторов.
Описание. Джон Непер придумал записывать результаты умножения из таблицы на отдельных палочках, и они стали самостоятельным вычислительным устройством. Использование палочек Непера на колесах с шестеренчатым зацеплением стало этапом на пути развития механических калькуляторов.
Счетные палочки Непера используются в Лаборатории математики Политеха в кружке «Практическая математика» и на школьном занятии «О числах, формулах и приемах счета».
3. Часовые спуски

Кому будет полезно. 7-10 классы.
Какие темы помогут понять. Геометрическая прогрессия, определение времени, устройство часовых спусков, зубчатая передача.
Описание. Часовые спуски показывают часть часового механизма, с их помощью можно увидеть, как в часах организована точная периодичность колебаний маятника. Вскоре в Лаборатории математики появится занятие об истории измерения времени при помощи механизмов, и на нем участникам будет предложено разобраться с непростым устройством часов.
Часовые спуски используются в Лаборатории математики Политеха на школьном занятии «Об истории измерения времени».
4. Параболограф Кавальери

Кому будет полезно. 7-11 классы.
Какие темы поможет понять. Квадратичная функция, свойство высоты прямоугольного треугольника.
Описание. При первом построении графика функции y = x2 в школе часто предлагают отметить несколько точек, принадлежащих графику, а потом плавной линией их соединить. А Лаборатория математики располагает инструментом, помогающим провести эту плавную линию и построить идеальную параболу.
Параболограф Кавальери используется в Лаборатории математики Политеха на интенсиве «Объемная алгебра», которое пройдет 3, 4 и 5 ноября и на школьном занятии «Парабола».
5. Эллиптический бильярд

Кому будет полезно. 3-11 классы.
Какие темы поможет понять. Оптическое свойство эллипса и его применение в технике и медицине.
Описание. Все конические сечения обладают оптическими свойствами. Например, зеркало в форме эллипса собирает лучи, выпущенные из одного фокуса во втором.
На занятиях «Теория голодной козы» для 4-7-х классов и «Замечательные кривые» для 7-11-х классов можно проследить траекторию любого луча — его моделью будет бильярдный шар.
6. Сумма углов треугольника

Кому будет полезно. 7-8 классы.
Какие темы поможет понять. Сумма углов треугольников.
Описание. Как найти сумму внутренних углов треугольника? Разрежьте треугольник на части и переложите их так, чтобы углы собрались у одной вершины. На занятии «Некоторые формулы геометрии» эта и другие модели-головоломки демонстрируют свойства фигур и наглядно доказывают формулы.
Источник: mel.fm