Как решаются задачи на скорость лодки

Большинство задач в математике решаются с использованием уравнений. При решении таких задач неизвестное данное обозначается переменной, остальные данные связывают с этой переменной, и таким образом получается уравнение.

При решении таких задач необходимо обязательно указывать, что взято за х, как переменная связана с другими данными в задаче, пояснять, как получилось уравнение.

Рассмотрим несколько задач на движение.

Задача 1.

Моторная лодка прошла 25 км по течению реки и 3 км против течения, затратив на весь путь 2 часа. Какова скорость лодки в стоячей воде, если скорость течения реки равна 3 км/ч?

Пусть х км/ч – скорость лодки в стоячей воде. Тогда скорость лодки по течению (х+3) км/ч, а против течения (х – 3) км/ч.

Время измеряется как частное от деления пути на скорость. Поэтому можно заметить, что по течению реки 25 км лодка прошла за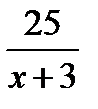

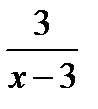часа, а против течения 3 км – за часа. Значит, время, затраченное на весь путь, равно 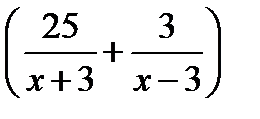часам. По условию задачи на весь путь лодка затратила 2 часа, значит, .

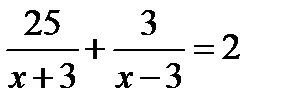Задачи на движение по воде. Виды скоростей. Как решать задачи по математике в 5 классе. Часть 17.

Решим это уравнение.

Очевидно, что х=2 не подходит, так как скорость лодки против течения (х – 3) км/ч, т.е. 2–3= –1, а скорость не может быть отрицательным числом.

Итак, скорость лодки в стоячей воде равна 12 км/ч.

Задача 2.

Из Червеня в Березино (см. рис.) выехал автобус, а через 10 мин — маршрутное такси, скорость которого на 20 км/ч больше скорости автобуса. Найдите скорости автобуса и такси, учитывая, что они приехали в Березино одновременно.

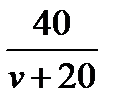По рисунку находим, что путь от Червеня до Березино составляет 40 км. Пусть v км/ч — скорость автобуса. Тогда скорость такси равна (v +20) км/ч. Автобус был в пути ч, такси — ч.

В соответствии с условием задачи разность между временем движения автобуса и временем движения такси составляет 10 мин, т. е. ч. В результате получаем уравнение .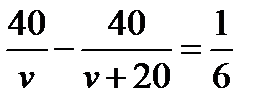

Решим это уравнение:

При этих значениях v знаменатели дробей, входящих в уравнение, не равны нулю. Значит, числа −80 и 60 являются корнями уравнения. Из них только второе число удовлетворяет условию задачи, поскольку скорость автобуса должна быть положительной. Поэтому скорость автобуса равна 60 км/ч, скорость такси — 80 км/ч.

Задачи на движение по воде | ЕГЭ 2022 по математике

В шахту брошен камень, и звук от его удара был услышан спустя 9 с. Определите глубину шахты, считая скорость звука равной 320 м/с, а ускорение силы тяжести g равным 10м/с 2 .

Для нахождения глубины шахты достаточно определить время t падения камня, так как глубина шахты согласно закону свободного падения равна метрам.

По условию g =10м/с 2 , поэтому глубина шахты равна 5t 2 метрам. С другой стороны, глубину шахты можно найти, умножив скорость звука на время его распространения от момента удара камня до момента, когда был услышан звук, т.е. на

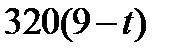секунд. Следовательно, глубина шахты равна метрам. Приравнивая два найденных выражения для глубины шахты, получаем уравнение 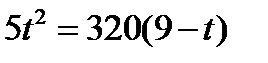. Решим это уравнение:

.

.

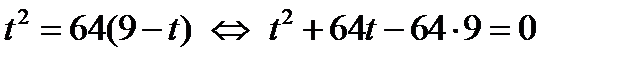
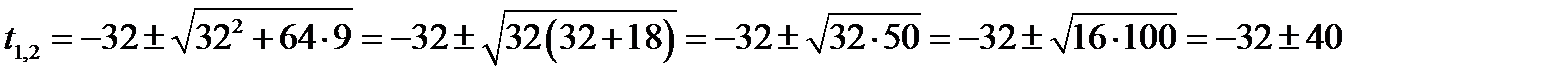
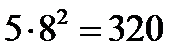
Так как время падения камня положительно, то t=8 с. Следовательно, глубина шахты равна 5t 2 = м.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник: studopedia.ru

Как решаются задачи на скорость лодки

1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.

Смотрите также конспект 9 класса по теме «Задачи на прямолинейное равномерное движение с решениями»

Физика 7 класс: все формулы на трех страницах

1 файл(ы) 255.55 KB

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Задача № 1. Ласточка летит со скоростью 36 км/ч. Какой путь она преодолеет за 0,5 ч?

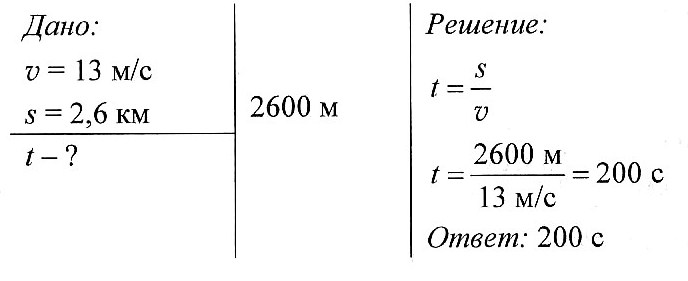
Задача № 1. Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?

Задача № 3. Автомобиль «Чайка» развивает скорость до 160 км/ч, а почтовый голубь — до 16 м/с. Сможет ли голубь обогнать автомобиль?

Решение. Чтобы сравнить скорости движения тел, надо перевести их в одинаковые единицы измерения. Перевод скорости из одних единиц в другие выполняют следующим образом. 160 км = 160000 м, 1 ч = 3600 с. Следовательно, за 1 с автомобиль пройдет путь 160000 : 3600 = 44 (м), значит:

Ответ: Голубь не обгонит автомобиль, так как 16 м/с < 44 м/с.

Задача № 4. Вдоль дороги навстречу друг другу летят скворец и комнатная муха. На рисунке представлены графики движения скворца (I) и мухи (II). Пользуясь графиком, определите:

1) Каковы скорости движения скворца и мухи?
2) Через сколько секунд после начала движения они встретятся?
3) Какое расстояние они пролетят до места встречи?

Решение.
1. Скорость движения скворца определим по формуле v=S/t. Выберем на графике произвольное время и определим, какое расстояние за это время пролетел скворец. Видно, что за 5 с скворец пролетел 100 м. Тогда

Аналогично найдем скорость движения мухи:

2. Точка А (точка пересечения графиков движения) соответствует моменту встречи. Скворец и муха встретятся через 4 секунды.

3. Скворец до места встречи пролетит расстояние SI = 80 м. Муха пролетит расстояние SII = 100 м — 80 м = 20 м.

Ответ: 1) скворец 20 м/с, муха 5 м/с, 2) через 4 с, 3) скворец 80 м, муха 20 м

Задача № 5. Определите среднюю скорость движения плота, если за 20 минут он переместился на 900 м. Скорость выразить в км/ч.

Ответ: Средняя скорость плота 2,7 км/ч.

Задача № 6. Стоящий на эскалаторе человек поднимается за 2 мин, а бегущий по эскалатору — за 40 с. За какое время этот человек поднимется по неподвижному эскалатору?

ОТВЕТ: 1 мин.

Решение. Стоящий на эскалаторе человек за 1 мин перемещается на половину длины эскалатора, а бегущий — перемещается на полторы длины эскалатора. Следовательно, идущий по неподвижному эскалатору человек за 1 мин перемещается как раз на длину эскалатора.

Задача № 7. Моторная лодка за 3 ч проходит расстояние от города до поселка, расположенного ниже по течению реки. Сколько времени займет обратный путь, если скорость движения лодки относительно воды в 4 раза больше скорости течения?

ОТВЕТ: 5 ч.

Решение. Обозначим скорость течения v . При движении по течению скорость лодки относительно берега равна 5v , а при движении против течения ее скорость равна 3v . Следовательно, время движения против течения в 5/3 раза больше, чем время движения по течению.

Задача № 8 (повышенной сложности). Рыбак плыл по реке на лодке, зацепил шляпой за мост, и она свалилась в воду. Через час рыбак спохватился, повернул обратно и подобрал шляпу на 4 км ниже моста. Какова скорость течения? Скорость лодки относительно воды оставалась неизменной по модулю.

ОТВЕТ: 2 км/ч.

Решение. Удобно рассматривать движение шляпы и лодки относительно воды, потому что относительно воды шляпа неподвижна, а скорость лодки, когда она плывет от шляпы и к шляпе, по модулю одна и та же — так, как это было бы в озере. Следовательно, после поворота рыбак плыл к шляпе тоже 1 ч, т. е. он подобрал шляпу через 2 ч после того, как уронил ее. По условию за это время шляпа проплыла по течению 4 км, откуда следует, что скорость течения 2 км/ч.

Задача № 9 (олимпиадного уровня). Из городов А и Б навстречу друг другу по прямому шоссе одновременно выехали два велосипедиста. Скорость первого 10 км/ч, скорость второго 15 км/ч. Одновременно с велосипедистами из города А вылетела ласточка.

Она долетает до второго велосипедиста, разворачивается, Долетает до первого велосипедиста и летает так между ними до тех пор, пока велосипедисты не встретятся. Какой путь пролетела ласточка, если скорость ее движения 50 км/ч, а расстояние между городами 100 км? Временем разворота ласточки можно пренебречь.

ОТВЕТ: 200 км.

Решение. Расстояние между велосипедистами каждый час уменьшается на 25 км. Поскольку начальное расстояние между ними 100 км, они встретятся через 4 ч. Все это время ласточка будет летать со скоростью 50 км/ч, следовательно, ее путь составит 200 км.

Алгоритм решения задач на движение

При решении других задач прямолинейного равномерного движения в общем виде нужно придерживаться следующего алгоритма: 1) выбрать систему отсчёта; 2-3) определить начальные координаты и значения скоростей движения тел в этой системе отсчёта; 4) записать зависимости координат тел от времени; 5) записать в виде уравнения условие задачи; 6) объединить уравнения; 7) решить эти уравнения; 8) провести анализ полученного результата (после чего выяснить, имеет ли полученный результат физический смысл); 9) если в условии задачи даны числовые значения, необходимо подставить их в полученное выражение и получить числовой ответ.

Анализ полученного результата заключается в исследовании зависимости искомой величины от входящих в ответ величин.

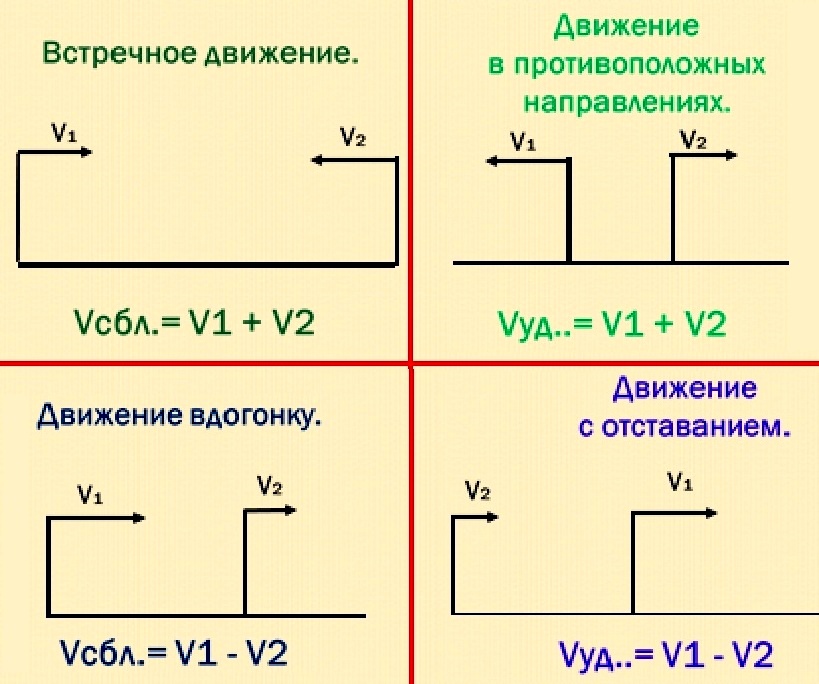
Не стоит забывать и про направление движения в зависимости от типа задачи (встреча, погоня, обгон, отставание)

Конспект урока «Задачи на движение с решением».

Источник: uchitel.pro

Теплоход проходит по течению реки

В состав ЕГЭ по математике включёна целая группа задач, относящаяся к задачам на движение — это задачи на движение по воде. Задачи несложные, решаются по той же формуле. Мы уже рассматривали с вами задачи на движение « Задачи на прямолинейное движение. Часть 1 » и другие. Принципы те же. Используется основная формула:

Но в задачах на движение по воде (по реке), добавляется лишь небольшое условие. Необходимо учитывать скорость течения реки. Скорость судна определяется следующим образом:

Если плыть по течению реки, то к скорости судна в неподвижной воде необходимо прибавить скорость течения.

Если плыть против течения, то из скорости судна в неподвижной воде необходимо вычесть скорость течения.

Так же необходим навык быстрого решения квадратного уравнения. На самом ЕГЭ это сэкономит ваше время. Иногда требуется извлечь корень из большого числа, по этому поводу изучите статью « Извлекаем корень из большого числа » .

От пристани А к пристани В отправился с постоянной скоростью первый теплоход, а через 2 часа после этого следом за ним со скоростью, на 2 км/ч большей, отправился второй. Расстояние между пристанями равно 168 км. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч.

Примем скорость первого теплохода за х км/ч. Тогда скорость второго теплохода равна х + 2 (км/ч).

Расстояние оба проехали одинаковое — 168 километров.

Осталось записать время.

Поскольку t = S/v, то первый затратит 168/х часов, а второй 168/(х + 2) часов.

Сказано, что через два часа после отправления первого, в путь отправился второй, то есть он затратил время на движение на два часа меньше:

Умножаем левую и правую части на х(х + 2)

Решаем квадратное уравнение:

Скорость есть величина положительная, значит, она равна 12 (км/ч).

*В этой задаче понятия «скорость течения» отсутствует и она от задач на движение по суше практически ничем не отличается.

Моторная лодка прошла против течения реки 120 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.

Пусть скорость лодки в неподвижной воде равна х.

Тогда скорость движения моторки по течению равна х + 1, а скорость, с которой она движется против течения х – 1.

Расстояние и в ту, и в другую сторону одинаково и равно 120 км.

Занесем скорость и расстояние в таблицу.

Заполняем графу «время».

При движении по течению затраченное на путь время равно 120/(х + 1), при движении против течения 120/(х – 1).

Причем 120/(х + 1) на 2 часа меньше, чем 120/(х – 1).

Да это и логично, что время на движение по течению реки затрачивается меньше.

Это уравнение имеет два корня: х 1 = 11 х 2 = –11 (оба этих числа при возведении в квадрат дают 121). Но, конечно же, отрицательный ответ не подходит — скорость лодки должна быть положительной: 11 км/ч

Теплоход проходит по течению реки до пункта назначения 560 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часа, а в пункт отправления теплоход возвращается через 56 часа после отплытия из него. Ответ дайте в км/ч.

Пусть скорость теплохода в неподвижной воде равна x (км/ч). Всего теплоход затрачивает 56 часа (на весь путь: туда, два часа стоянки, обратно). То есть:

56 = (ПО ТЕЧЕНИЮ) + (СТОЯНКА) + (ПРОТИВ ТЕЧЕНИЯ)

Скорость движения теплохода по течению равна х+4 (км/ч), а скорость против течения х – 4 (км/ч).

Расстояние и в ту, и в другую сторону одинаково и равно 560 км.

Занесем скорость и расстояние в таблицу. Заполняем графу «время».

Время, затраченное на путь до пункта назначения 560/(х + 4),

Время, затраченное на путь обратно (против течения) 560/(х – 4).

Таким образом, скорость теплохода в неподвижной воде равна 24 км/ч.

Как извлекать корень из большого числа без калькулятора можно посмотреть здесь.

Теплоход проходит по течению реки до пункта назначения 459 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 22 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 54 часов после отплытия из него. Ответ дайте в км/ч.

Скорость течения реки как искомую величину принимаем за x (км/ч).

Тогда скорость движения теплохода по течению равна 22 + х (км/ч), а его скорость против течения 22 – х.

Расстояние в ту, и в другую сторону одинаковое и равно 459 км.

Всего теплоход затрачивает 54 часов (на весь путь: туда, 10 часов стоянки, обратно). То есть:

54 = (ПО ТЕЧЕНИЮ) + (СТОЯНКА)+ ( ПРОТИВ ТЕЧЕНИЯ)

Расстояние и в ту, и в другую сторону одинаково и равно 459 км.

Занесем скорость и расстояние в таблицу. Заполняем графу «время».

Время, затраченное на путь до пункта назначения 459/(22+х),

Время, затраченное на путь обратно (против течения) 459/(22–х).

Подставляем данные и получаем уравнение: