Как рассчитать силу удара

Сила удара определяется как ситуация, когда совершается некоторая работа по перемещению объекта на определенное расстояние. Его можно интерпретировать как силу, возникающую при столкновении двух предметов. Столкновение объектов происходит, когда один объект сталкивается с другим. Ударная сила оказывает огромное воздействие на объект за короткий промежуток времени.

Он обозначается символом F. Его единицей измерения являются ньютоны (Н), а размерная формула задается как [M 1 L 1 T -2 ]. Его формула равняет произведение массы и скорости тела на удвоенное время. Другими словами, это отношение кинетической энергии, которой обладает тело, к пройденному им расстоянию.

Формула силы удара

F = mv/2t

where,

F is the impact force,

m is the mass of the body,

v is the velocity of the body,

t is the time taken.

Вывод

Consider an object of mass m which moves with a velocity v when some work W is done on it. The force applied is F and it moves the object to a distance of d units for t seconds.

Как влияет кач на силу удара? Нокаутер Ростислав Плечко рассказывает правду Папе Смиту

We know the work done equals the product of force applied and distance travelled.

W = Fd ⇢ (1)

Also, the work done equals the kinetic energy of the body.

W = K.E. = 1/2 mv 2 ⇢ (2)

From (1) and (2) we get,

Fd = 1/2 mv 2

F = mv 2 /2d

Putting d = vt, we get,

F = mv 2 /2vt

F = mv/2t

This derives the formula for impact force acting on a body.

Примеры проблем

Задача 1: Рассчитайте силу удара, действующую на предмет массой 2 кг со скоростью 4 м/с в течение 2 секунд.

Решение:

Задача 2. Рассчитайте силу удара, действующую на предмет массой 3 кг со скоростью 8 м/с в течение 3 секунд.

Решение:

Задача 3. Рассчитайте массу тела, если сила удара, действующая на тело, равна 10 Н, а скорость равна 5 м/с в течение 4 секунд.

Решение:

Задача 4: Вычислите скорость тела, если сила удара, действующая на тело, равна 14 Н, масса равна 2 кг в течение 2 секунд.

Решение:

Задача 5. Вычислите время, затрачиваемое телом, если сила удара, действующая на тело, равна 30 Н, масса 4 кг и скорость 15 м/с.

Решение:

Задача 6. Рассчитайте силу удара, действующую на тело с кинетической энергией 20 Дж, если пройденное расстояние равно 2 м.

Решение:

Задача 7. Вычислите кинетическую энергию тела, если сила удара, действующая на тело, равна 40 Н, а пройденное расстояние равно 4 м.

Решение:

Источник: progler.ru

Как рассчитать силу удара боксёра в кг?

А то всё говорят, к примеру: удар пришёлся с силой в 20 кг, 100 кг, 1000кг .

Как это рассчитывается.

Лучший ответ

во первых сила измеряется в ньютонах, во вторых удар характеризуется не силой а импульсом силы J=Ft, т. е. результат удара зависит не только от приложенной силы, но и от времени в течении которого она прилагалась. например, если вследствии удара тело массой 2 кг подскочило на 5 м, то изменение его количества движения равно mV=m(2gh)^1/2=20Нс и оно равно импульсу силы. если удар длился 0,1с, то средняя приложенная сила равна 20/0,1=200Н. с такой силой давит на опору тело массой 20 кг (т. к. F=mg), вот и говорят что удар силой 20 кг. если бы удар длился 0,02с, то сила бы была 200/0,02=1000Н и говорили бы что удар 1000/10=100 кг

ВЫ НАВСЕГДА ЗАПОМНИТЕ как подбирать силу удара в русском бильярде

Остальные ответы
Напольные весы распологаешь фронтально и бьешь. Циферблат фиксирует силу.)))

Есть автомат, за пять рублей бьёте по груше и вам показывают, сколько кг удар. Рассчитывается простыми весами, насколько стрелка отклонилась, настолько и удар.

Источник: otvet.mail.ru

Нужно рассчитать силу удара при падении в граммах.

Ответ. Формально это рассчитывается так; F=(m*v)/t; v=(2*g*h)^0,5; t- это время «взаимодействия тела и Земли в момент приземления»! Вот здесь и есть «ГЛАВНАЯ» «загвоздка»! При t=0, мы имеем F= бесконечность! Так- что!

Ваш вопрос не корректен!

Ну знаете ли, это ведь может зависить от нескольких факторов)

Bad-Boy Sexy-Boy

Ну, во-первых, сила в граммах не измеряется. Если уж и измерялась раньше, то в грамм-силах. А во-вторых, зависит еще от степени деформируемости поверхности, на которое это тело падает. Средняя сила рассчитывается элементарно F=m*g*h/S, где m — масса тела, g — ускорение свободного падения, h — высота падения, S — путь, пройденный при соударении с поверхностью.

Но это только в предположении, что сила остается постоянной на всем пути при деформации поверхности. На практике это далеко не так. Сопротивление воздуха, конечно, тоже имеет значение, потому что от этого зависит скорость соударения с поверхностью. Коэффициент сопротивления обычно считают пропорциональным квадрату скорости тела. А зависит он еще от многих факторов.

В частности от ФОРМЫ тела. Короче, рассчитать тебе это не удастся. Лучше не парься, а начни учить физику. С самого начала.

Источник: sprashivalka.com

II. Расчеты на удар тел

Продолжительность удара очень мала и сложно вычислить ускорения частиц ударяемой конструкции. Поэтому, воспользоваться принципом ДАламбера затруднительно и обычно здесь используют закон сохранения энергии.

Для удобства расчета на удар вводят условное понятие динамическая сила . Эта такая сила, которая, будучистатически приложенной в точке удара, вызовет такие же перемещения (деформации) ударяемого тела, как и при ударе.

Расчет на удар без учета массы ударяемого бруса

Рассмотрим закрепленный упругий брус, на который с высоты падает груз весом. При этом брус может испытывать: а) продольные деформации (колонны, сваи) рис. 9.1а, б) изгибные деформации (балки) рис. 9.1б.

После удара, когда груз останавливается в нижнем положении, деформации каждого сечения бруса достигают наибольших значений. Их обозначим:деформации в точке удара,в любом сечении бруса с координатой(на рис. 9.1б в эти деформации (прогибы) показаны сплошной линией). Затем происходят затухающие колебания бруса, в конце которых устанавливаются деформации

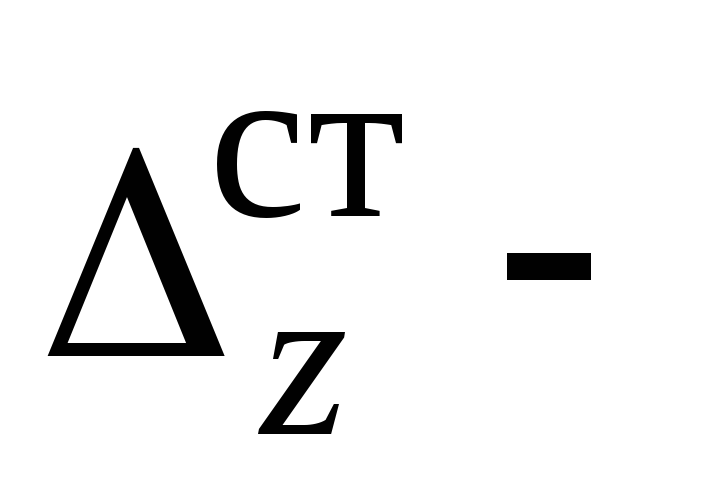(в точке удара) ив любом сечении, соответствующие статическому действию груза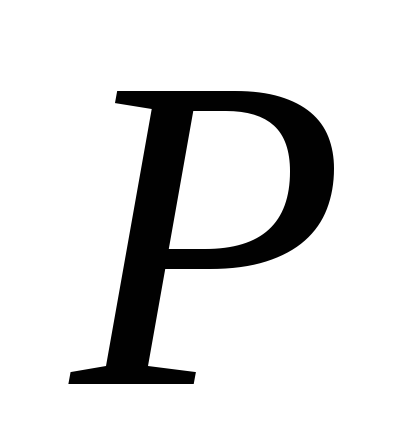(на рис. 9.1б эти деформации показаны пунктирной линией).

Расчет проведем при следующих допущениях:

1. Брус идеально упругий, справедлив закон Гука, модуль одинаков при динамическом и статическом нагружении;
2. Массу ударяемого бруса пока не учитываем;
3. Эпюра перемещений сечений бруса от удара подобна эпюре перемещений от статического действия груза . (На рис. 9.1б графики прогибов, обозначенные сплошной и пунктирной линиями, подобны). Обозначим

динамический коэффициент (9.3) Из третьего допущения и рис. 9.1б следует с учетом (9.3) (9.4) Согласно принятого выше определения динамической силы , от ее статического приложения возникнут деформации и , а от статического нагружения силойпоявятсяи. По закону Гука деформации пропорциональны нагрузкам, поэтому (6) По закону Гука и напряжения пропорциональны нагрузкам 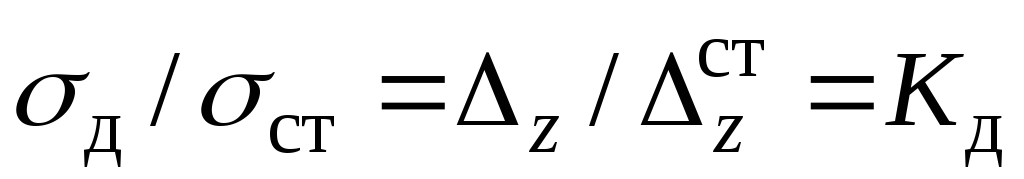(9.5) Здесь динамические напряжения, т.е. возникают в брусе при ударе;статические напряжения, возникают при статическом нагружении силой. Из (9.4) и (9.5) следует (9.6) Итак, деформации и напряжения в любом сечении бруса при ударе можно определить по (9.6), если вычислить динамический коэффициент. А деформациии напряженияпри любом виде статической нагрузки (осевой, изгибной, кручении и т.д.) мы умеем определять из вышеприведенных разделов. Для решения задачи используем закон сохранения энергии. Груз

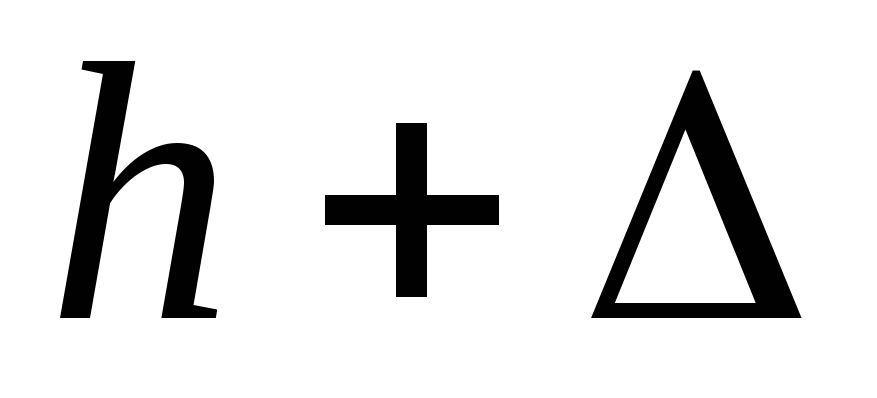при падении проходит путьи совершает работу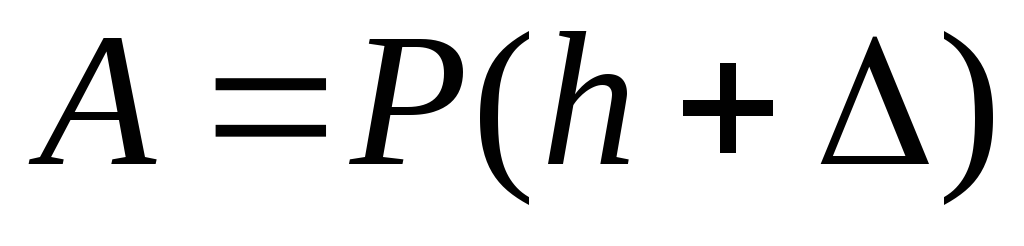. При статическом нагружении силой 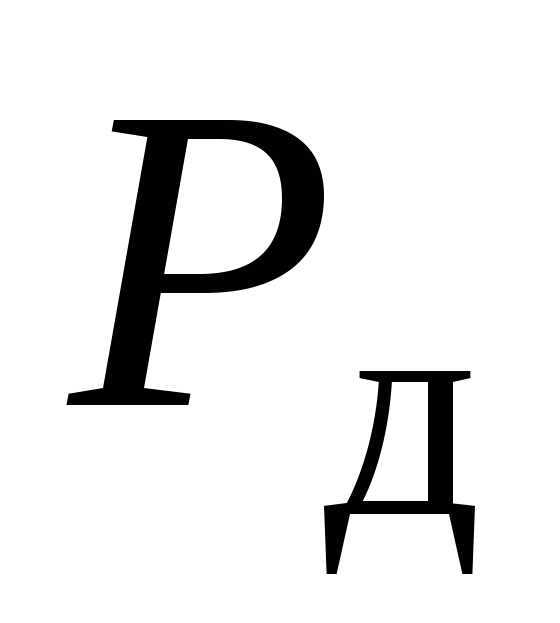получим ту же деформацию, что и при ударе, потенциальная энергия деформации бруса при этом, как известно, определяется так 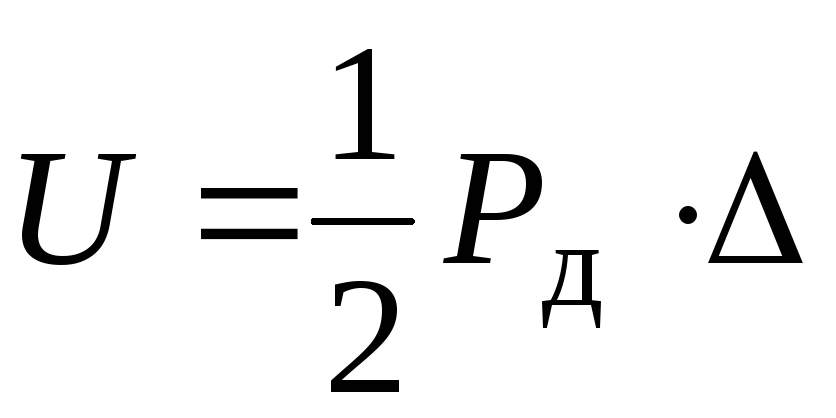. Сила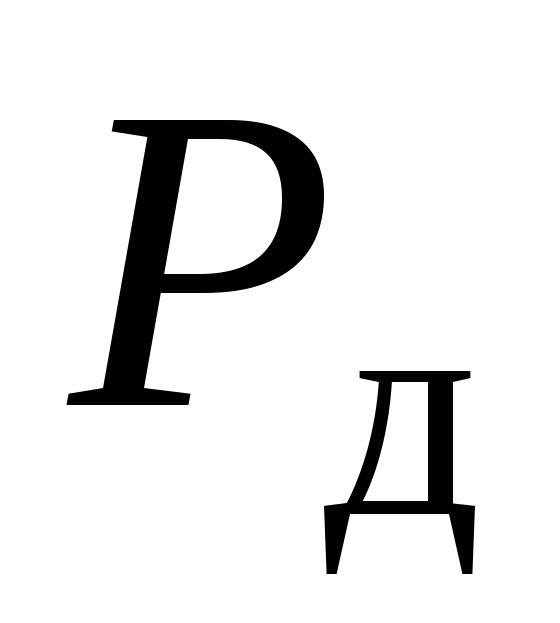прикладывается в т.К, куда падает груз 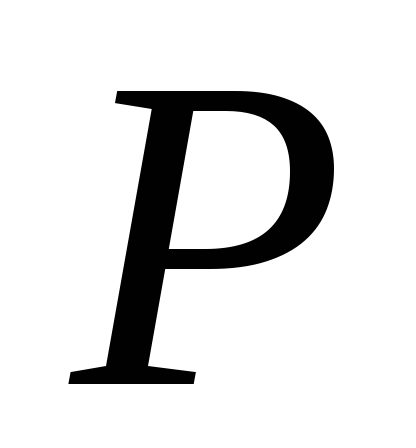. По закону сохранения энергии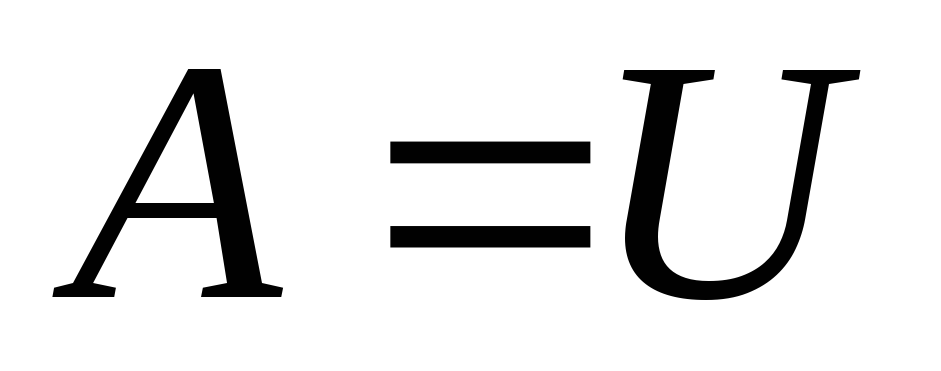, т.е. 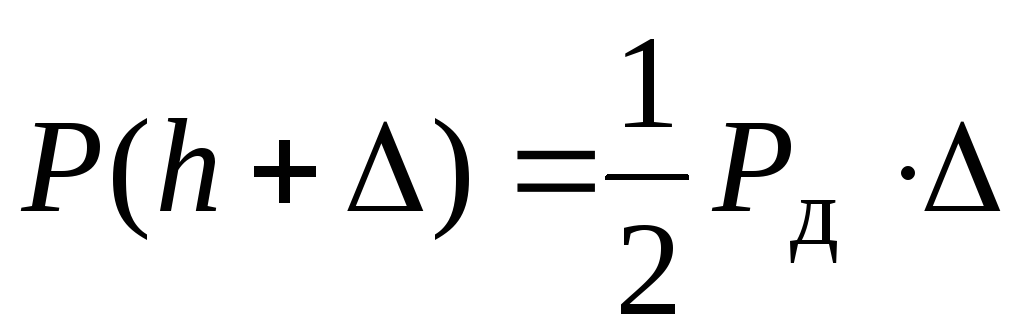(7) Из (6) 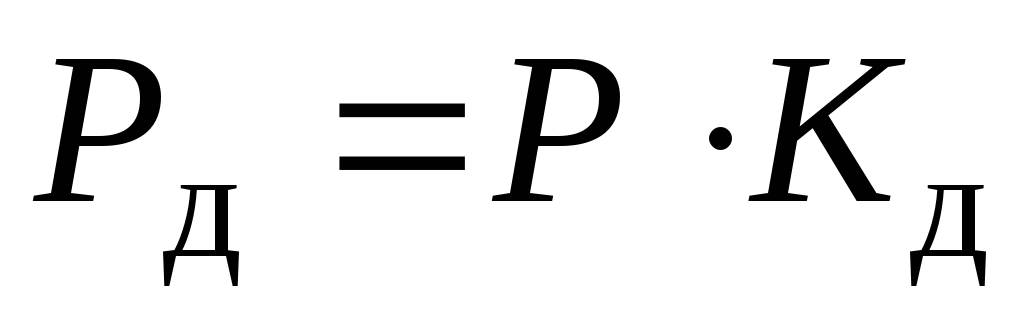, подставим в (7) получим 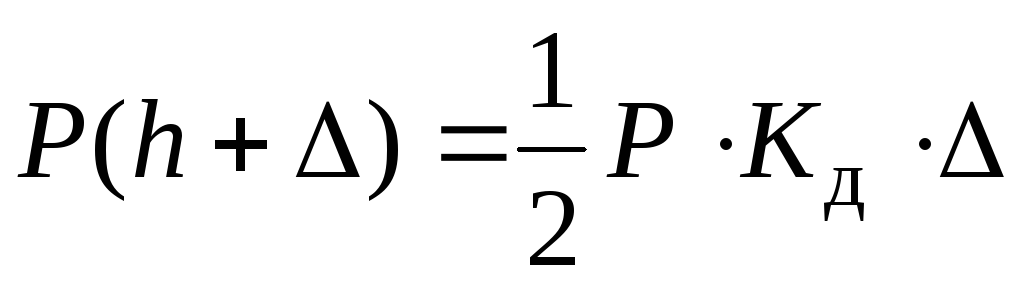(8) Сокращаем на 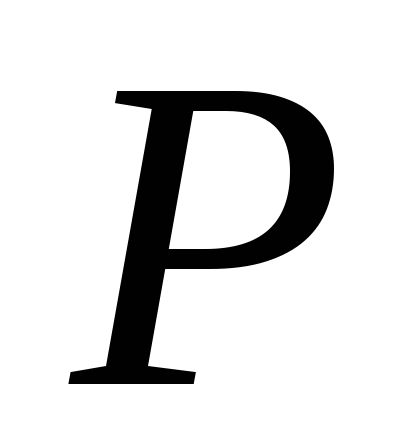и учитывая из (9.4), что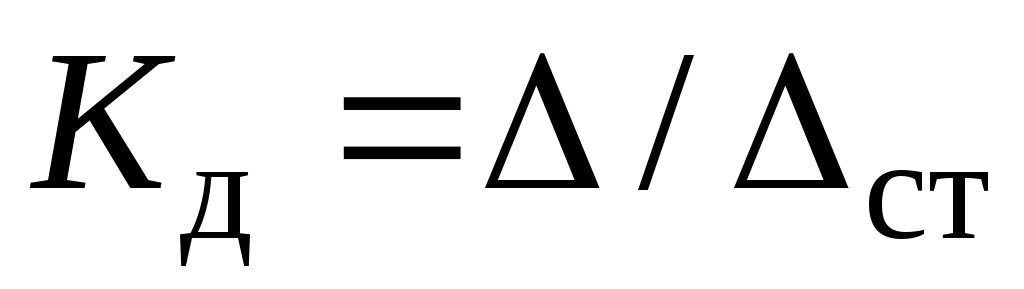найдем 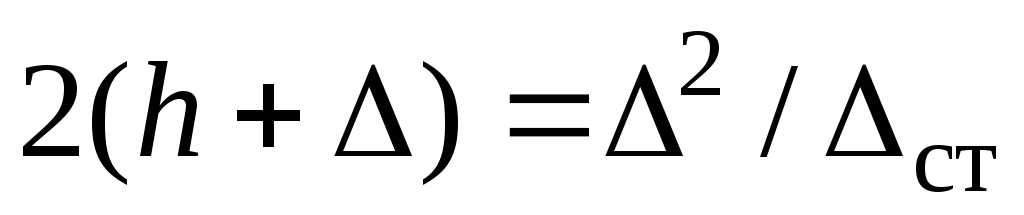или 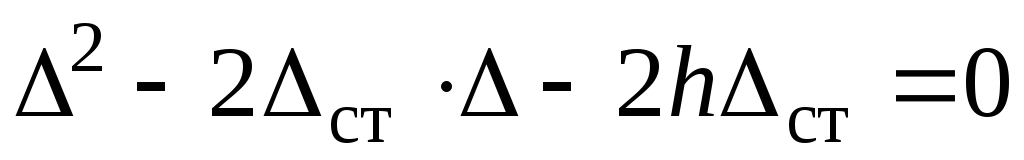(9) Относительно неизвестной получили стандартное квадратное уравнение типа 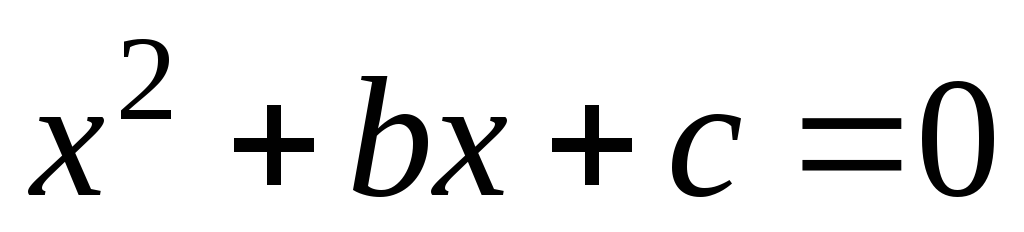Здесь 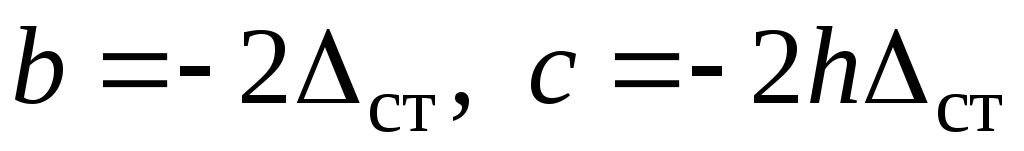. Решение квадратного уравнения известно из справочников: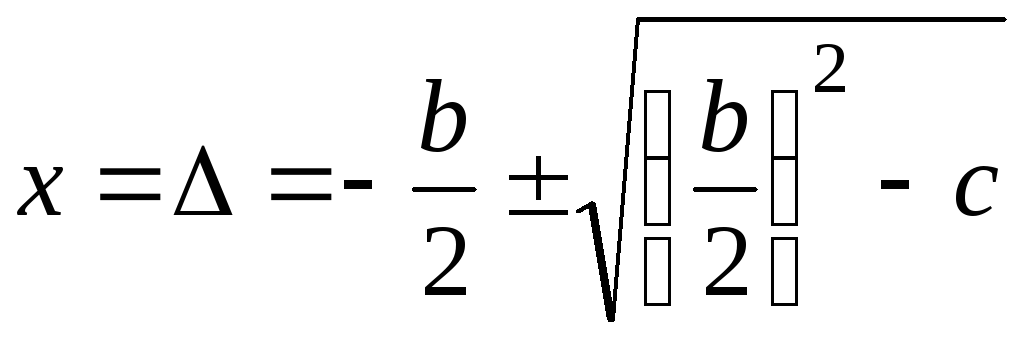. В нашем случае получим 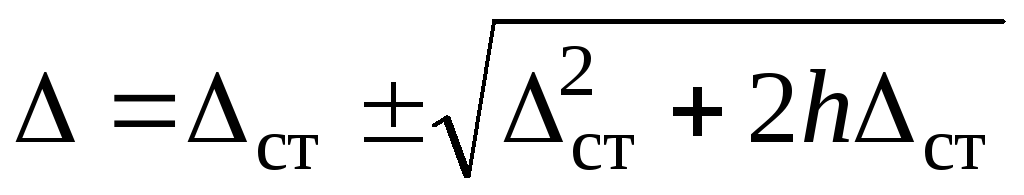(10) При ударе всегда 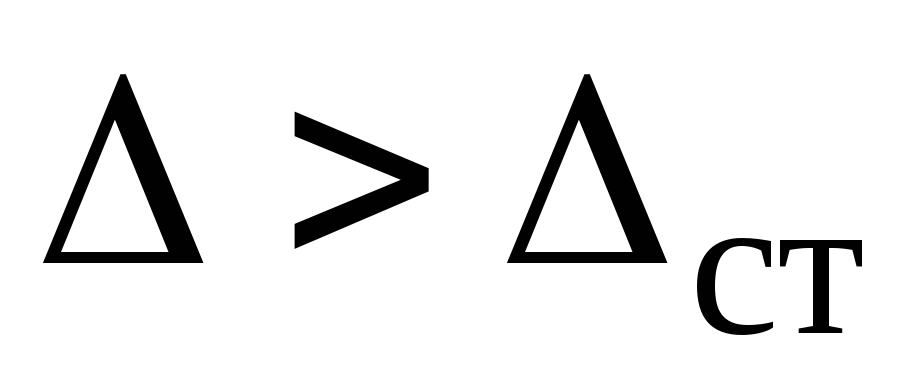, поэтому выбираем знак (+) и формулу (10) преобразуем так 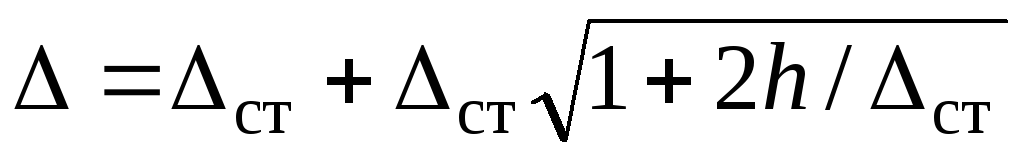или окончательно 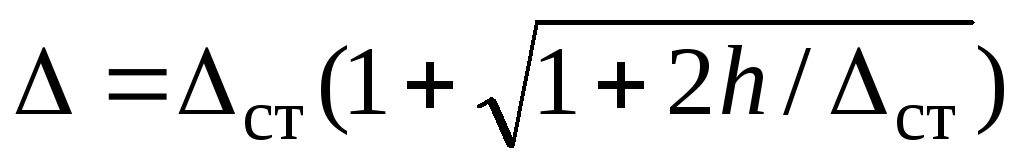(11) Согласно (9.4) 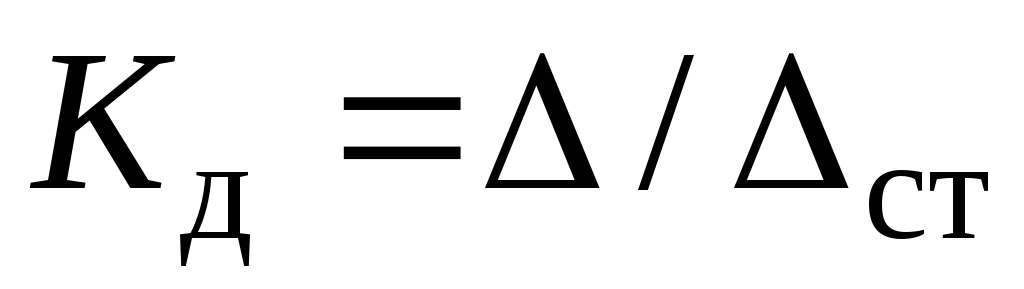, тогда из (11) получим 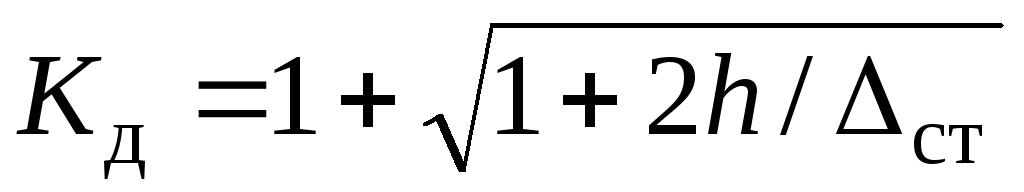(9.8) Величинаст  статическая деформация бруса в точке удара от статического приложения силы 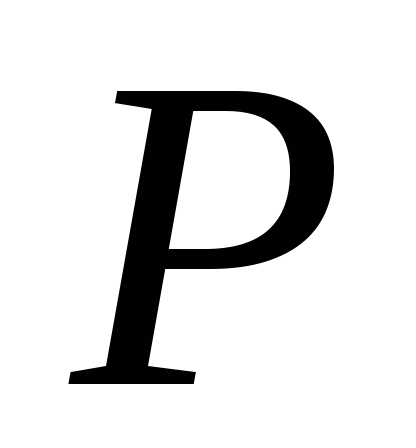в точке «K» падения груза весом 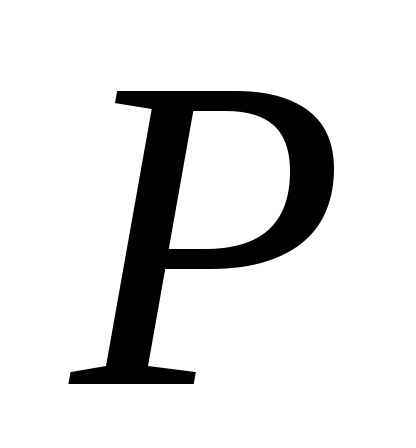. Определяется известными методами: Рис. 9.1а: По закону Гука при осевой нагрузке 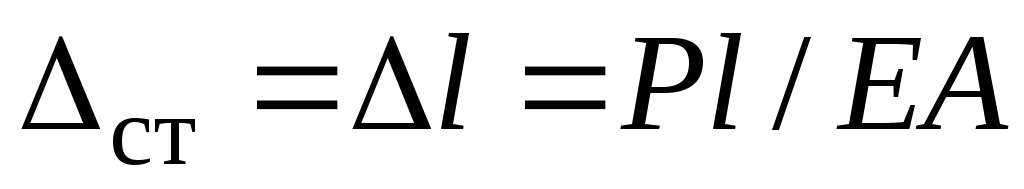Рис. 9.1б: 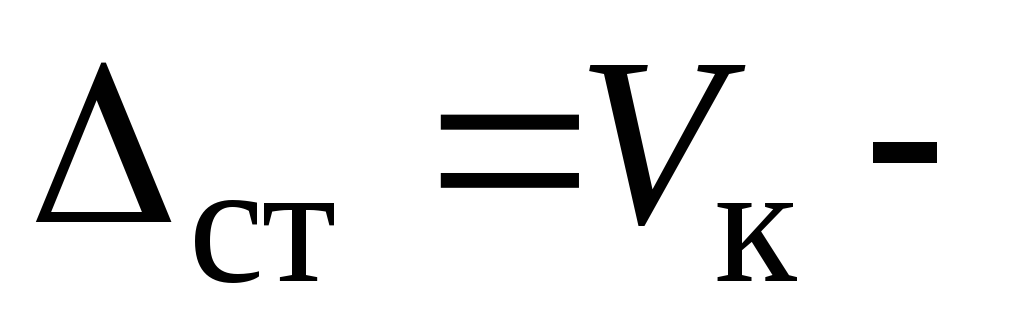прогиб балки в т. K от силы 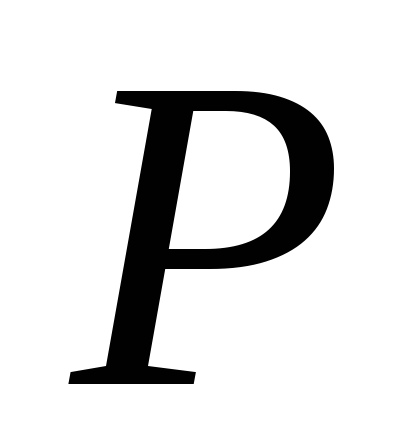, приложенной в т.K. Определяется известным методом Клебша из раздела «Плоский изгиб балок». Скорость груза, падающего с высоты 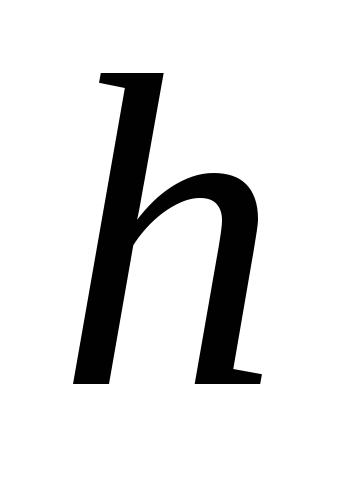, как известно, определяется так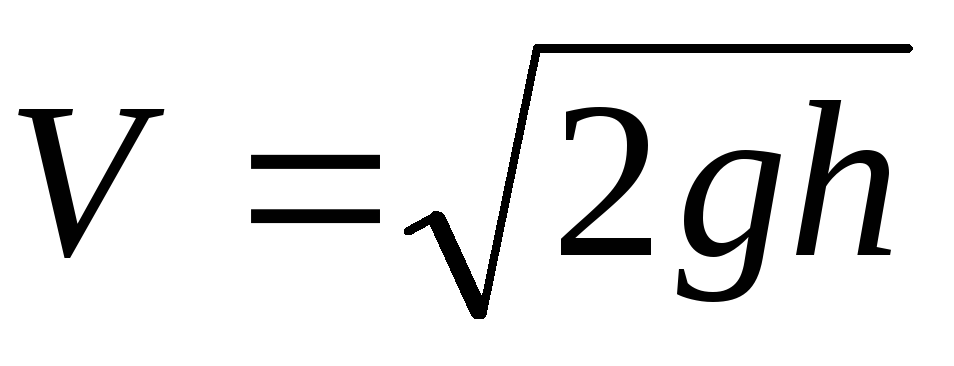, откуда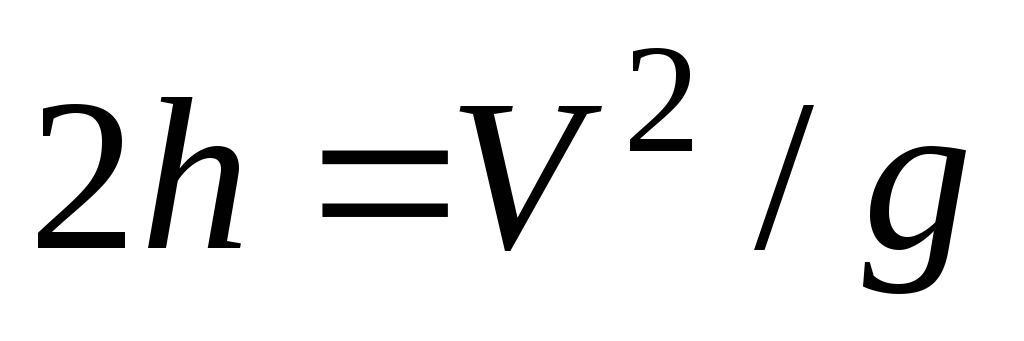. Подставим это в (9.8) получим 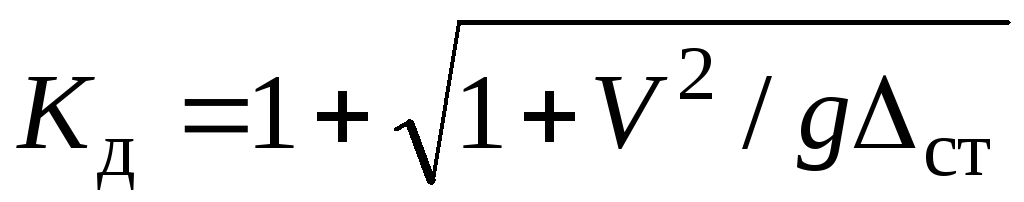(9.9) Преобразуем 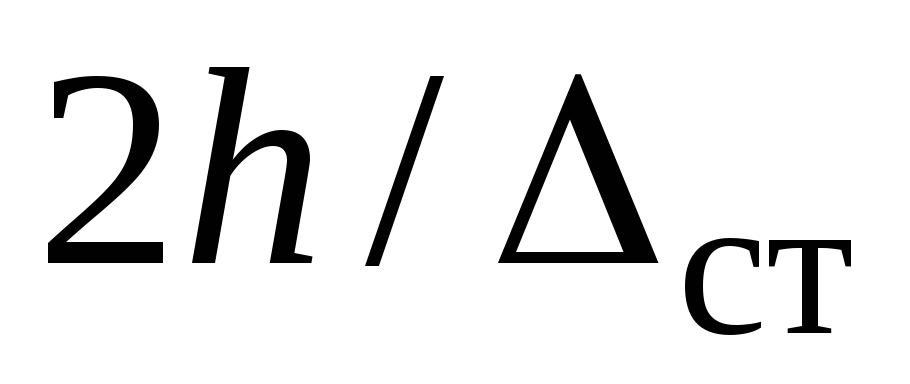так: 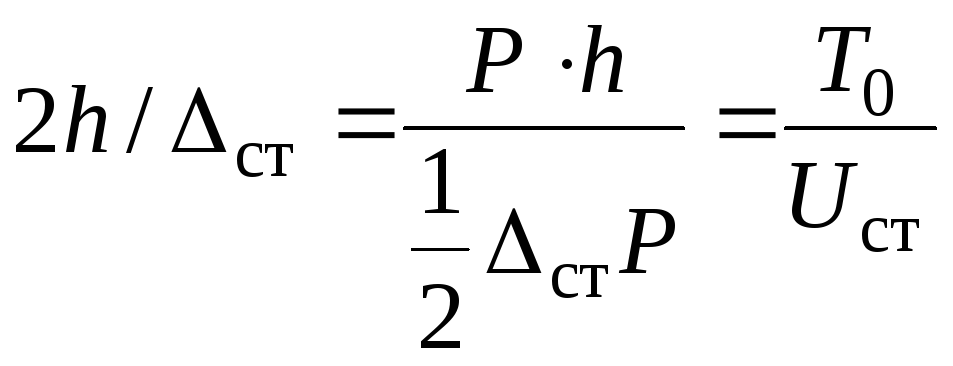(12) Здесь: 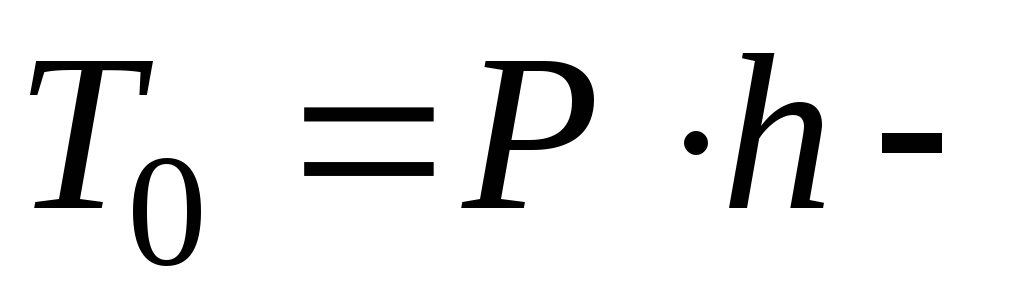энергия падающего груза в момент начала удара; 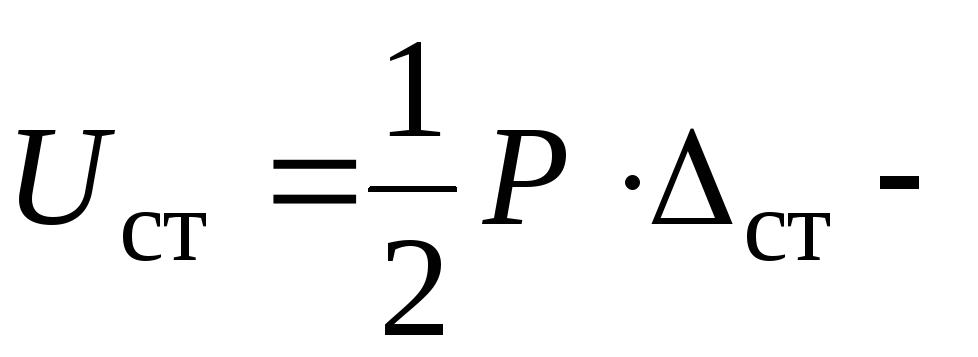потенциальная энергия деформации бруса от статического нагружения его силой 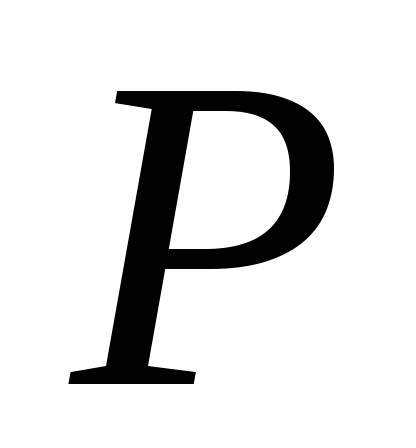в т.K. С учетом (12) из (9.8) найдем 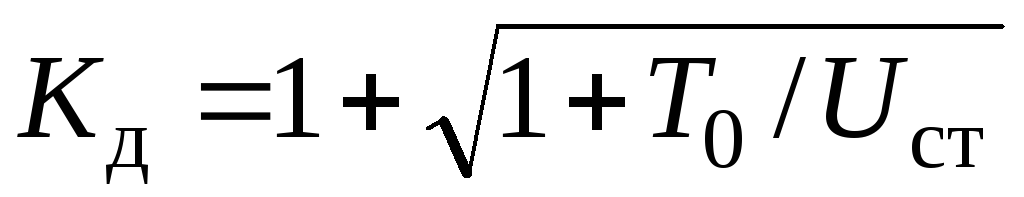(9.10) Из (9.8) следует, что чем больше , т.е. чем больше деформируется брус от статической нагрузки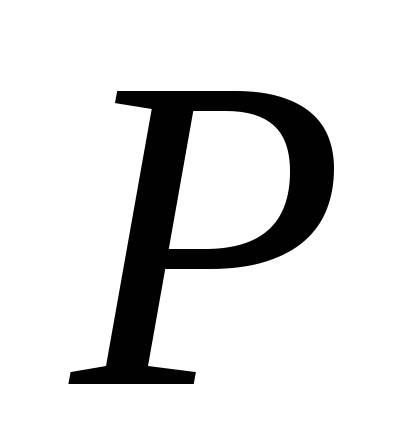, тем меньше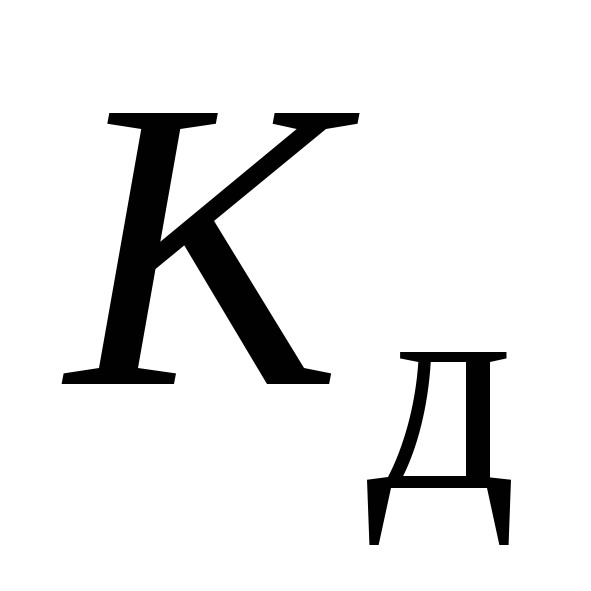и по (9.6) меньше напряжения при ударе. Так появилась идея ставить в конструкциях, испытывающих ударные нагрузки, различные амортизаторы, рессоры, пружины и поясняется поговорка «знал бы, где упаду, подстелил бы солому». Пример. Порядок расчета балки на удар.

P	На балку с высоты в т.K падает груз . Найтимаксимальное напряжение в балке от удара, максимальные прогибы в пролете и консоли. В т. K балки статически при-

кладываем силу 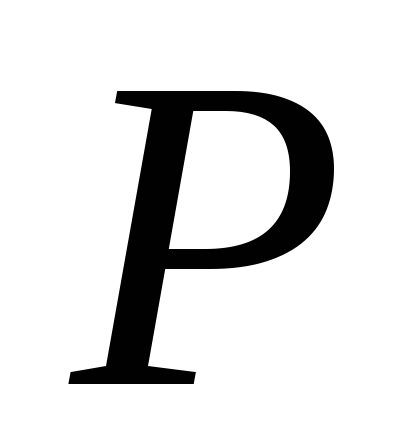, равную весу груза (рис.б). Определяем от нее опорные реакции и строим эпюруизгибающих моментов. Из Эп.находими, зная размеры и форму поперечного сечения балки, вычисляем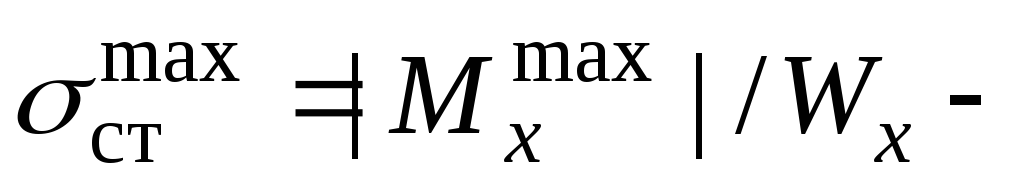максимальные напряжения от статического нагружения. Для вычислений по (9.6) надо знать. Для балки б) со статической силой для двух участков запишем дифференциальные уравнения изгибапо методу Клебша, интегрируем их и из условий закрепления балки находим константы интегрирования. Строим график прогибов балки, приблизительный вид которого показан на рис.б. Находим

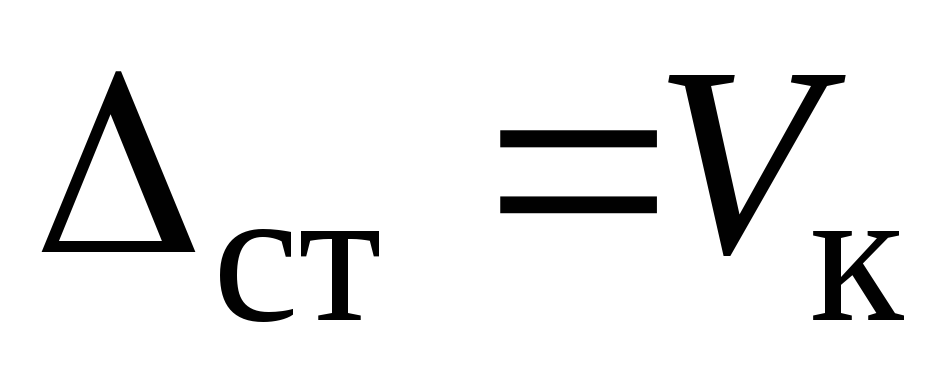прогиб балки в сечении «K», это и есть . По (9.8) вычисляем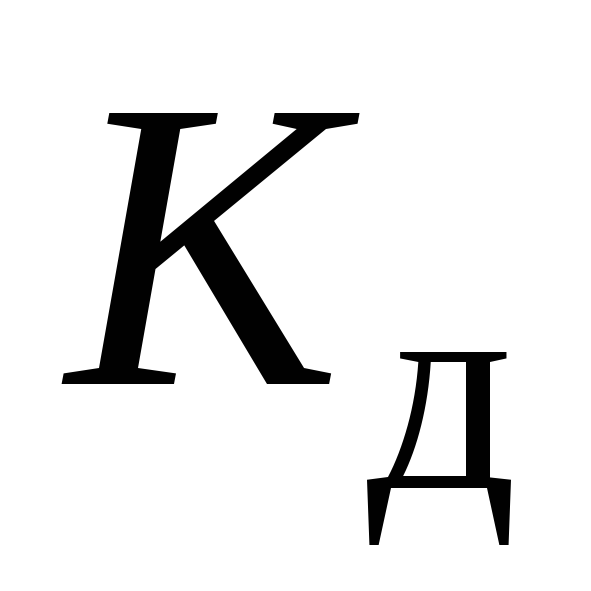и далее 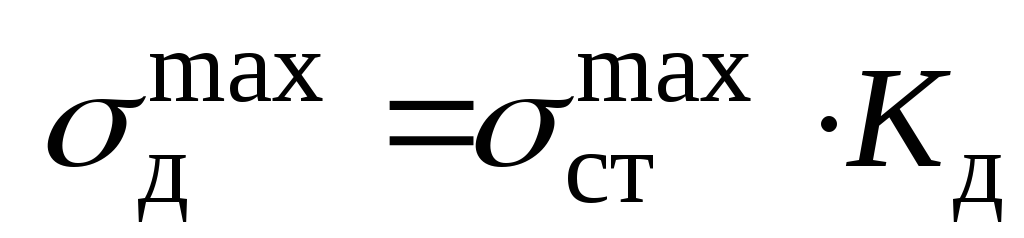В консоли максимальный прогиб при ударе 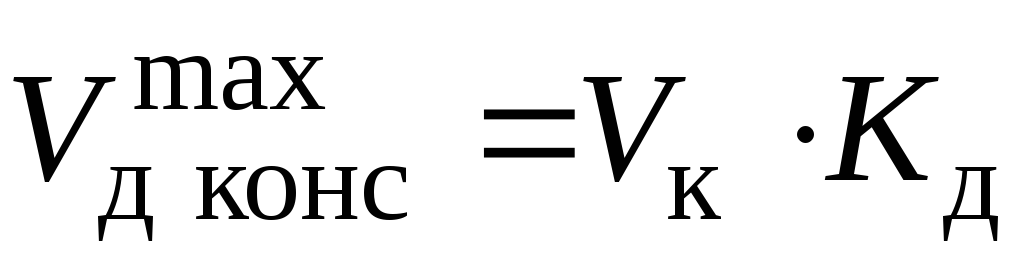. В пролете находим 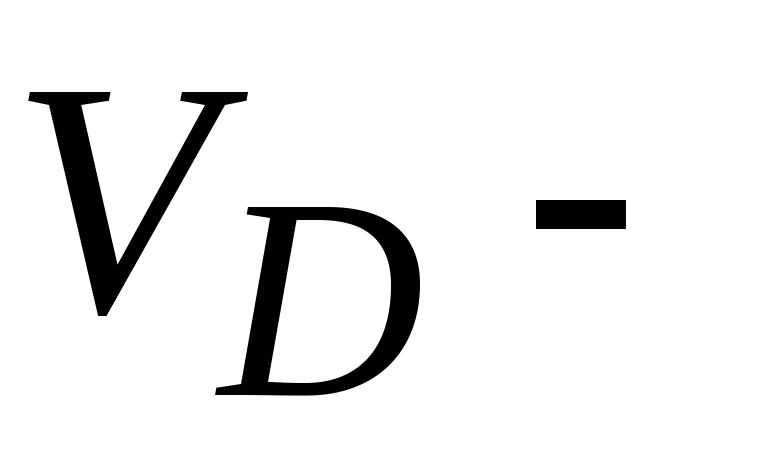максимальный прогиб от статического нагружения и далее максимальный прогиб при ударе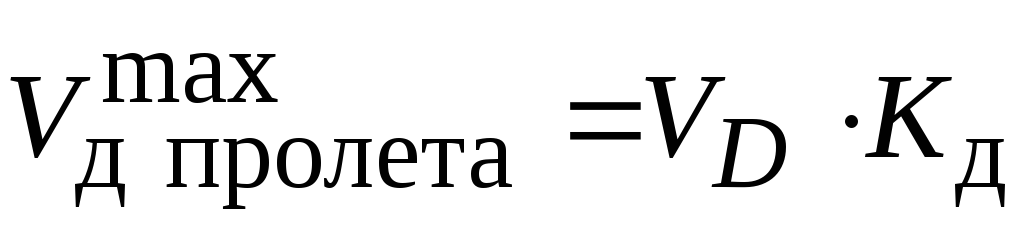. Дальше можно проверить балку на прочность и жесткость обычными методами. Существует термин «падение с высоты 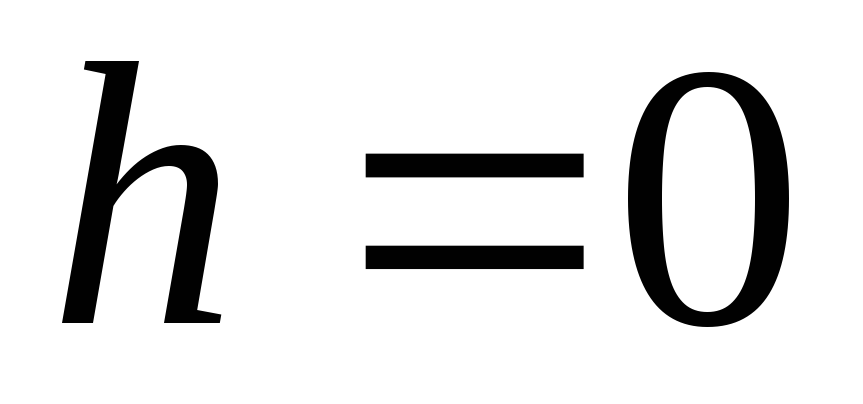». Из (9.8) в этом случае получим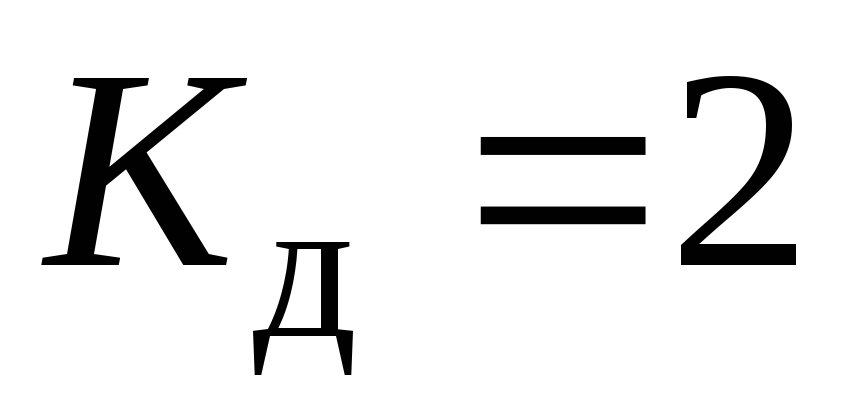. Чтобы этого не было, груз надо опускать плавно не только до соприкосновения с конструкцией, но и дальше, при перемещении груза вместе с деформируемой конструкцией до полной их остановки. Учет массы ударяемого тела(бруса) Учет массы ударяемого тела достаточно сложен, поэтому приведем окончательные формулы без вывода их. Динамический коэффициент в этом случае определяется по формулам, аналогичным (9.8)-(9.10) 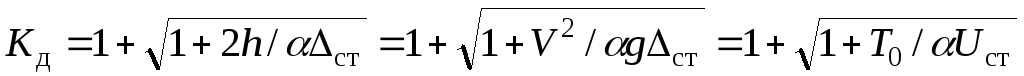(9.11) Здесь: 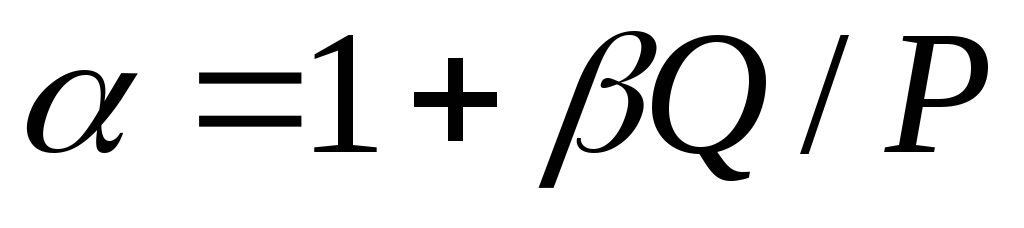; 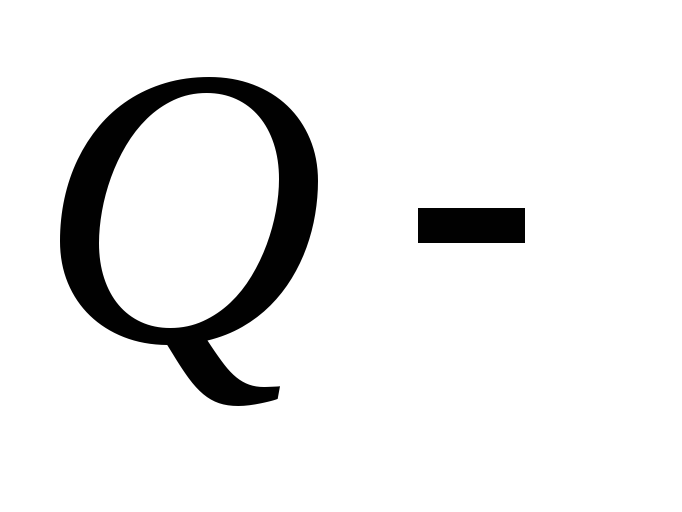вес ударяемого тела, для бруса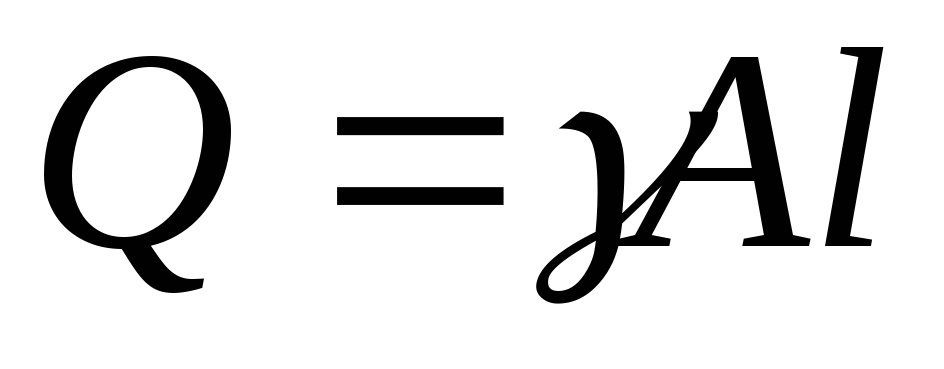 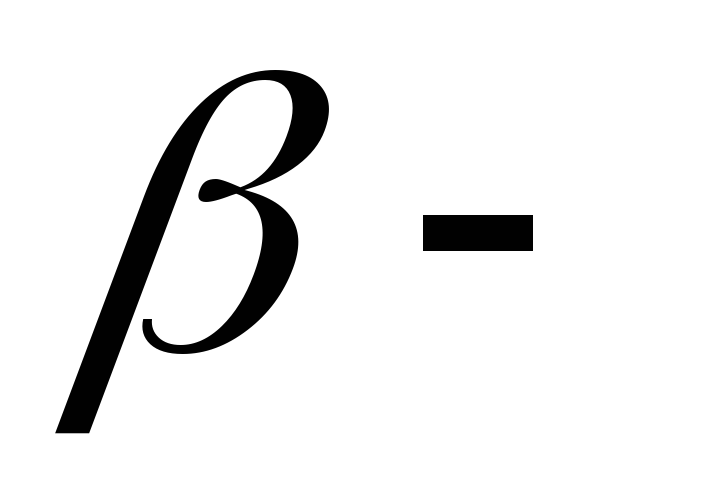редукционный коэффициент, определяется так 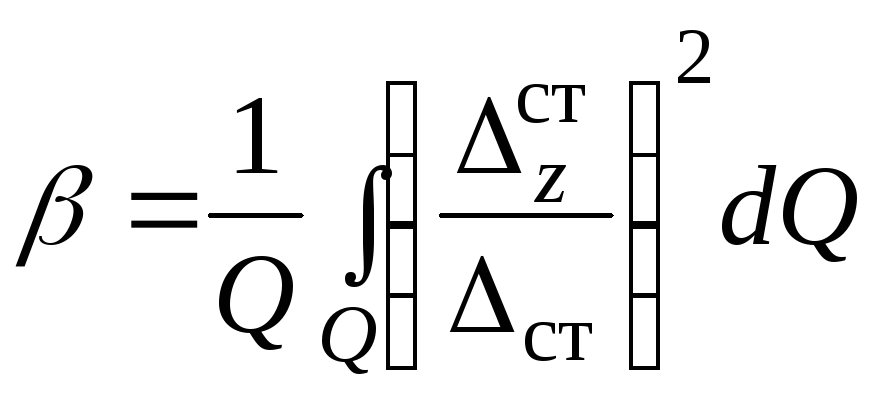, для бруса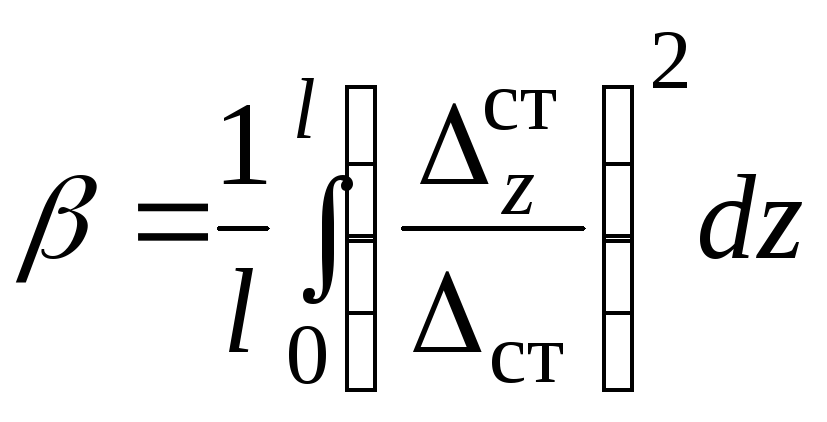(9.12) Вычислив , определяем коэффициенти далее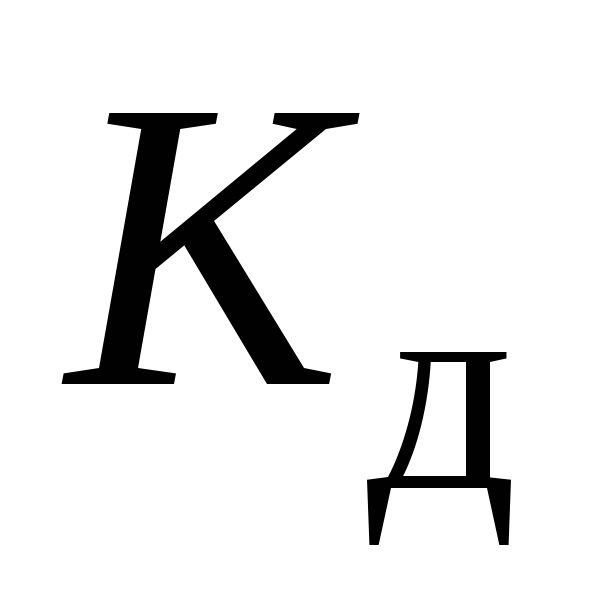. Пример 1. Вычислить для колонны, показанной на рис. 9.1а. По закону Гука для сечения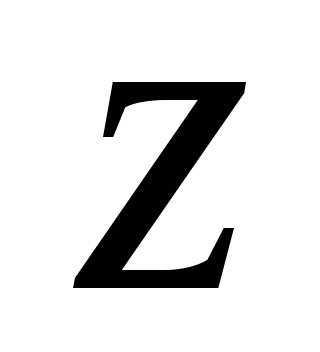от статического нагружения силой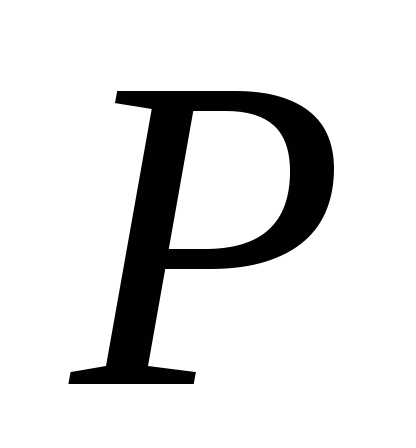: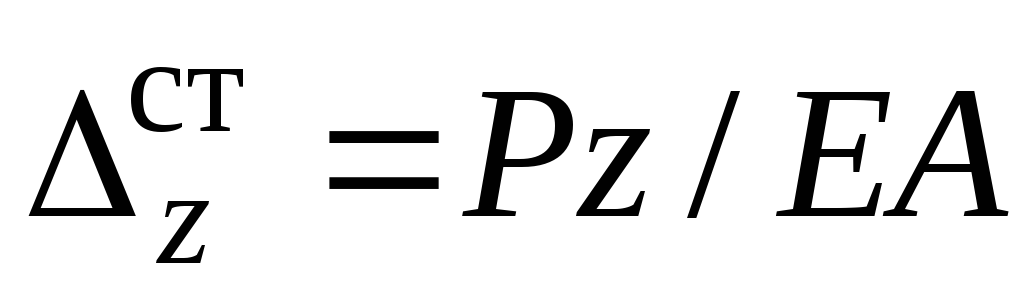,,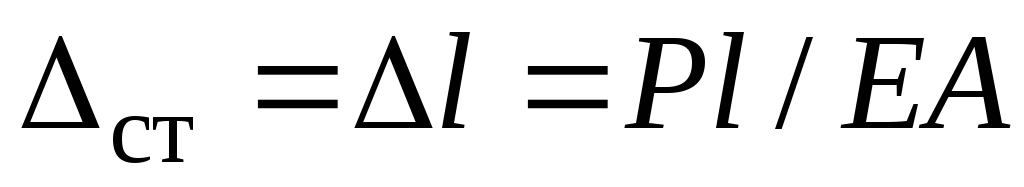 где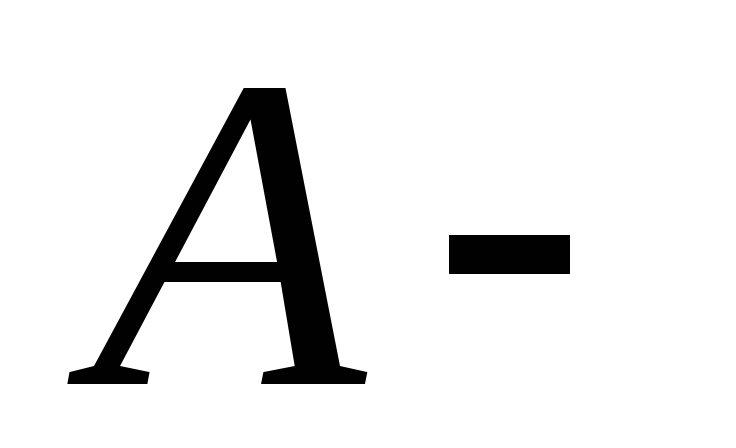площадь поперечного сечения колонны,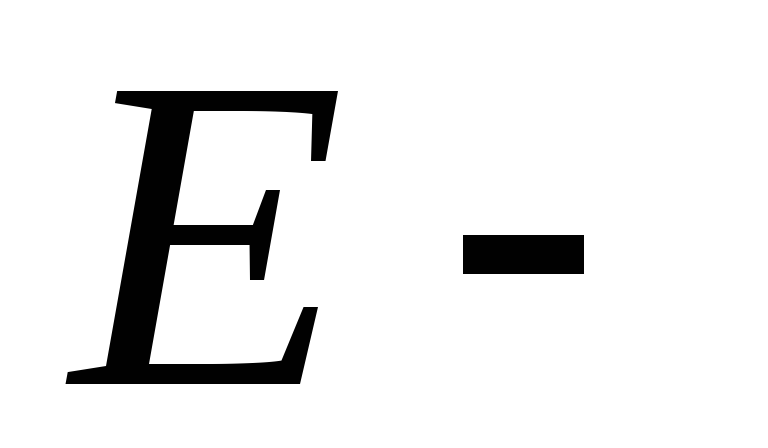модуль упругости материала. 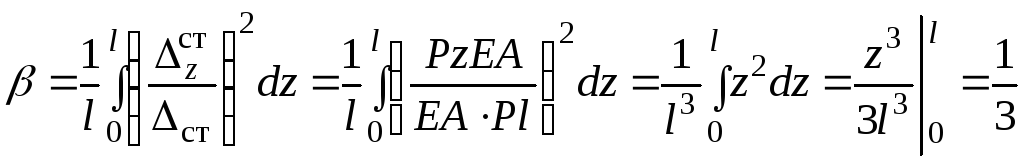. Пример 2. Вычислить для балки, показанной на рис. 9.1б, когда груз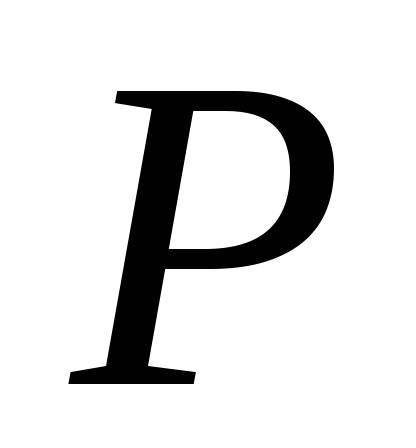падает на середину балки. Опорные реакции 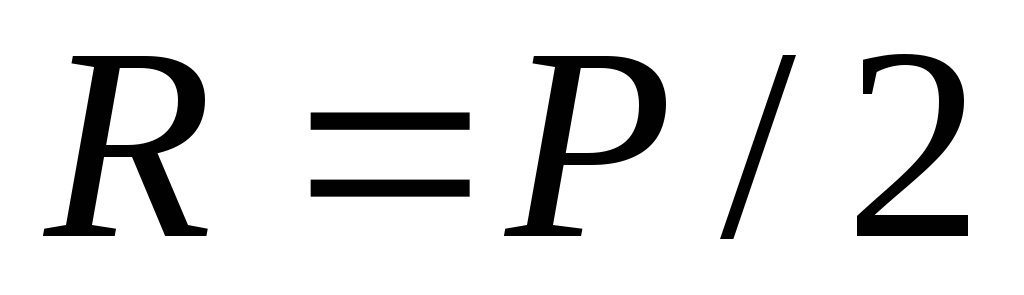, дифференциальные уравнения изгиба балки от статического нагружения силой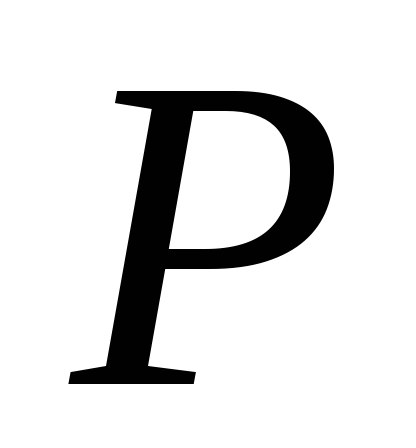: 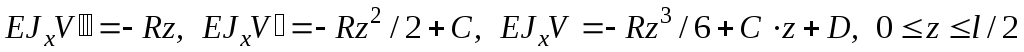, т.е. ввиду симметрии ограничимся одним участком. Граничные условия: 1) 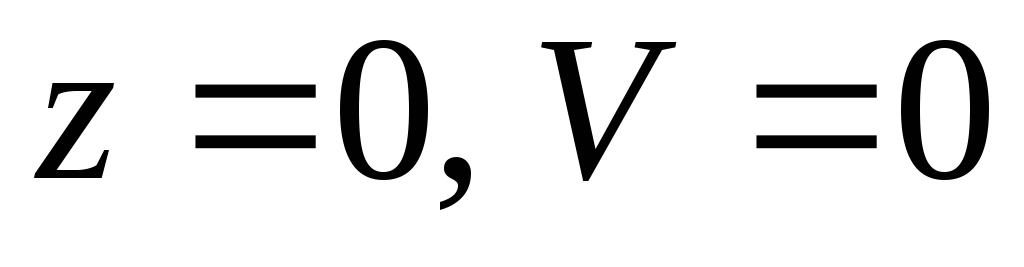; 2)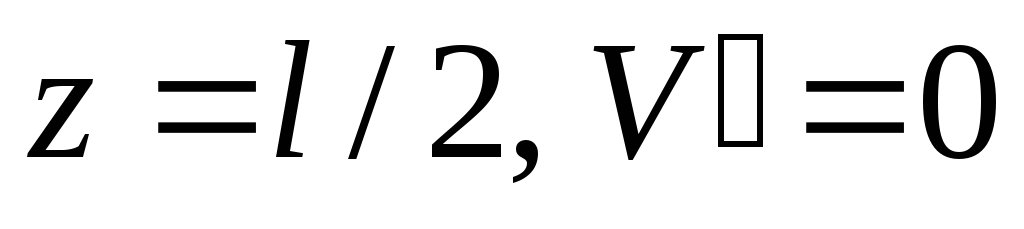(ввиду симметрии), откуда найдем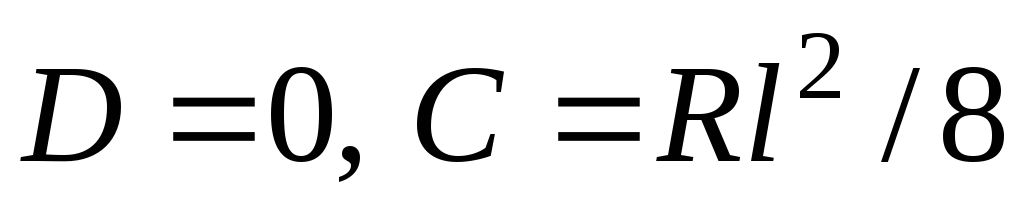. 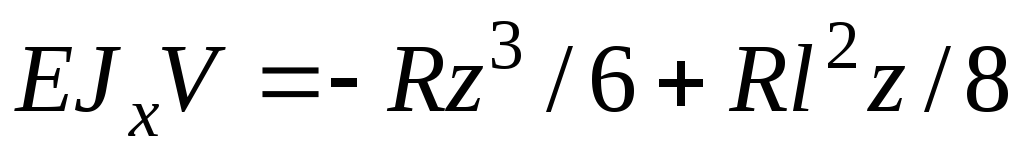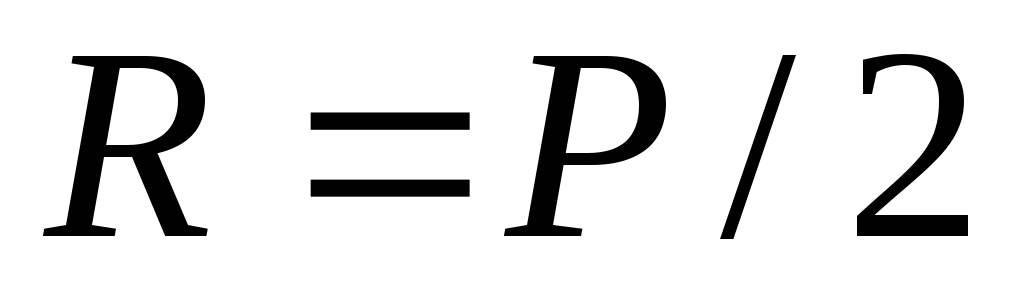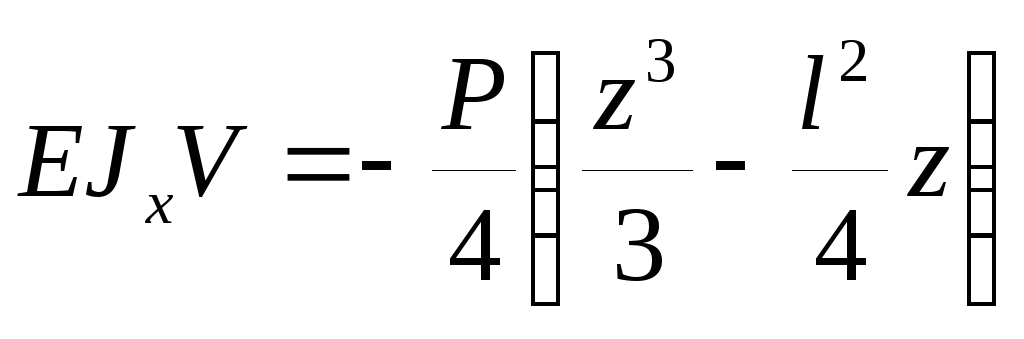Тогда, т.к., то, а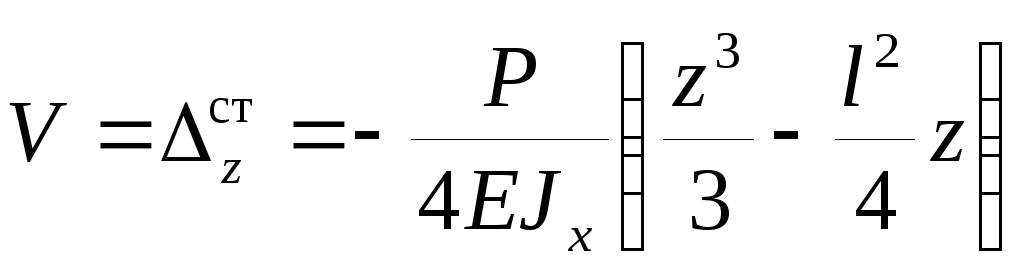, подставим 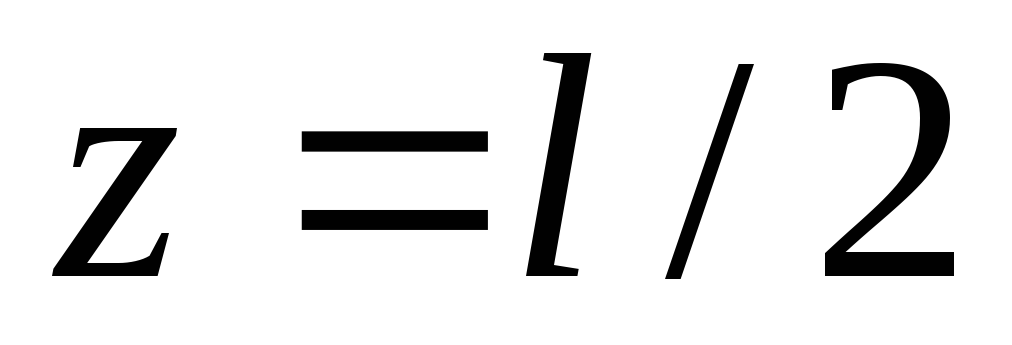получим: 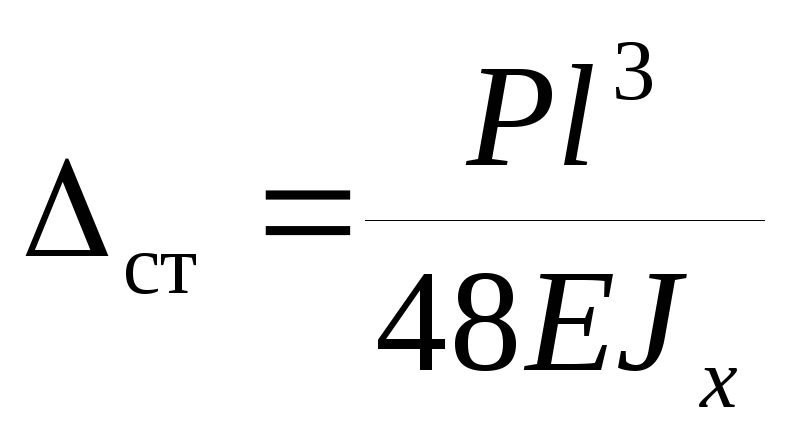; Найдем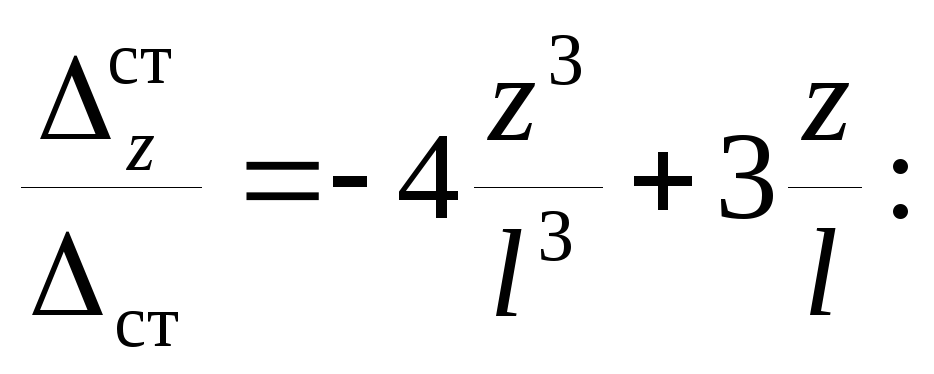 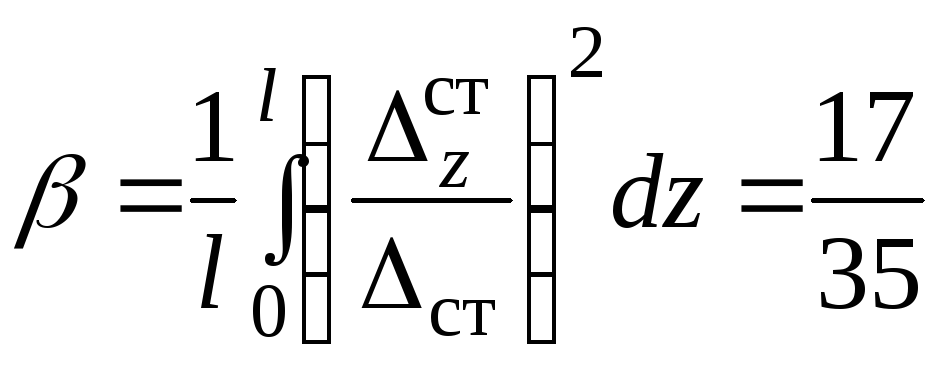. Все полученные выше формулы приближенные. Чем большей жесткостью обладает ударяемый брус, тем менее точными будут результаты расчетов. Более точные результаты получаются при рассмотрении волновой теории удара.

Источник: studfile.net

Что такое «сила удара»?

Как «взрывная сила» — это не сила, а скорость нарастания силы (масса*рывок), так и «сила удара» с чисто физической точки зрения вообще не сила, а совсем даже количество движения (масса*скорость). Что невольно запутывает людей, поэтому они зачастую начинают применять силовые тренировки там, где они вовсе не требуются. Мол, нам нужна большая «сила удара», а силовые тренировки развивают силу, поэтому возьмём штангу. Логично, чо.

Для простоты представим бодибилдера, который наносит удар одной рукой (ноги-то при ударах не важны, ха-ха). Пусть он бьёт рукой как боксёр, то есть без напряжения антагонистов, тогда угловая скорость сокращения трицепса будет что-то вроде 1000 гр/с (17,5 рад/с). Если длина предплечья с кулаком равна 40 см, тангенциальная скорость кулака получится 7 м/с. При весе кулака в 0,3 кг его удар будет обладать количеством движения 2,1 кг·м/с. А удар 51-килограммового боксёра-любителя может обладать количеством движения 29,5 кг·м/с.

В 14 раз больше. Как? Щас расскажу.

Скорость

У боксёров выше скорость. Непосредственно увеличить скорость сокращения мышцы нельзя, ибо генетика, а вот косвенных способов множество. Во-первых, упомянутое расслабление мышц-антагонистов. Во-вторых, так как удар является многосуставным движением, можно последовательно разгонять «ступени» тела от ног до руки.

Если вы кидаете мячик, передвигаясь на автомобиле, то скорость мячика будет равна скорость автомобиля + скорость броска. Соответственно, если к скорости сокращения трицепса прибавить скорость разворота плеч, вращения корпуса, бёдер и поступательного движения тела, то скорость для прямых ударов получится выше на 30-40% (9-10 м/с). А боковые удары вообще почти исключительно за счёт вращения бёдер и корпуса наносятся и имеют скорость в районе 15 м/с.

И вот тут как раз очень важна техника: нужно не просто последовательно подключать разные части тела, но делать это в единственно правильный момент. Если вы подключите, например, корпус раньше или позже, то разгон от ног вы потеряете.

В бейсболе, кстати, где всё определяется скоростью броска, тоже самое:

И если почитать что-нибудь о бросках в бейсболе (раз, два, три), то можно многое узнать о важности задней ноги как генератора силы, и передней ноги, как «тормоза», позволяющего повернуться вокруг него бедрам, тазу и корпусу. Неправда ли, очень напоминает слова Хейслета о передней ноге как якоре, вокруг которого поворачивается тело?

Таким образом, с точки зрения скорости, сила ног (позволяющая концентрически разгонять тело задней ногой и эксцентрически тормозить передней для придания корпусу максимального вращающего момента) как раз-таки боксёру нужна. А сила рук — почти нет, потому что руки кидают перчатку, которая практически ничего не весит. Сила, определяемая поперечным сечением мышцы, позволяет ускорить движение при внешнем сопротивлении. Если его нет, то скорость сокращения мышцы определяется генетикой (количеством быстрым мышечных волокон). Превзойти этот порог никакой 50-см трицепс не поможет.

В-третьих, взрыв или скорость нарастания силы. То есть умение рекрутировать максимальное количество двигательных единиц за минимальное количество времени. Скорость сокращения мышечных волокон неизменна, но активируются (и разгоняют часть тела) они последовательно. Чем быстрее значительная часть МВ включится в работу, тем быстрее часть тела достигает максимальной скорости. Это нервно-мышечная координация, то есть по сути техника.

В-четвертых, выносливость. Ударить быстро один раз нетрудно, трудно сделать это сотню раз за раунд. Закисленная мышца сокращается в несколько раз медленнее, поэтому и скорость удара падает во столько же раз.

Масса

Как ни странно, благодаря правильной технике боксёры также часто обладают большей эффективной массой удара, чем качки: если руки они бросают максимально хлестко и расслабленно (скорость), то за мгновение до удара они наоборот фиксируют суставы и в противника прилетает что-то посущественнее кулака (масса). Как минимум, туда прилетает предплечье массой в несколько кг (если был зафиксирован лучезапястный сустав), а то и рука (если бы зафиксированы лучезапястный и локтевой) или рука с частью корпуса (если был зафиксированы лучезапястный, локтевой и плечевой суставы). Правда, в таком случае скорость бьющей конечности падает до скорости последнего сегмента, так что надо смотреть какое количество движения в итоге получается. Но, тем не менее, именно большая эффективная масса удара отличает нокаутёров.

Шейн Мозли, который спарринговался чуть ли не со всеми боксёрами, о спарринге с Головкиным (известным нокаутёром с процентом нокаутов выше 90):

По его словам middleweight Головкин бьёт как light heavyweight, то есть боксёр на две категории выше, и в ударах Головкина «ощущается большая масса». Как Головкин это делает? Благодаря гигантскому трицепсу и дельтам? Да нет, благодаря скиллу и, вероятно, генетике. Сам-то по себе он не особо быстрый.

Можно на ту же тему почитать и что-нибудь более академическое. Например, есть такое исследование Biomechanics of the head for Olympic boxer punches to the face, с прекрасной табличкой, над которой можно долго медитировать:

Наибольший интерес, конечно, представляет сравнение ударов боксёров веса мухи (до 51 кг) и супертяжеловесов (более 91 кг). Как видим, некоторые мухачи обладают эффективной массой удара больше некоторых супертяжей. Что поистине и удивительно.

Конечно, силовые тренировки вес руки увеличивают, но вы получите гораздо больший эффект, если научитесь вкладывать в удар не кулак, а как минимум предплечье. А то и руку с частью корпуса.

Как образно писали известные советские тренеры:

Тренер добивался, чтобы бьющая рука боксёра начинала движение вместе с вращением тела и опережала это вращение в конце удара (момент «экспрессии в ударе»), чтобы удар шел от плеча и локтя вместе с плечом, чтобы локоть и кулак двигались в одной плоскости или, как образно говорит мастер спорта В. Чудинов, чтобы боксёр «чувствовал локоть в кулаке».

Именно «бить локтём, а не кулаком» — один из лучших советов, который тренер может дать начинающему боксёру на мой взгляд, вместе с «отпусти руки, пусть летят».

Техника и тактика

Это было рассмотрение «силы удара» с точки зрения физики. Однако чаще всего под «сильными ударами» понимаются удары, приводящие к нокаутам.

Подобные удары, конечно, коррелируют с «физикой» (большим количеством движения в ударе), но не тождественны им, потому что для нокаута необходимо попасть вовремя (скилл), точно (скилл) и неожиданно для противника (скилл). Можно обладать чудовищный ударом, но иметь процент нокаутов меньше, чем физически не столь одарённый/подготовленный, но более умелый боксёр.

Впрочем, о технике и тактике удара подробно поговорим в следующий раз.

Источник: shadow-ru.livejournal.com