Дроби используют в математике, чтобы кратко обозначить часть рассматриваемой величины.
Но если есть часть, то обязательно есть и целое (то, отчего была взята эта часть).
Зная целое, можно найти его часть, указанную соответствующей дробью.
Запомните!
Чтобы найти дробь (часть) от числа, нужно это число умножить на данную дробь.
Пример. Рассмотрим задачу.
В книге 160 страниц. Юра прочитал
| 4 |
| 5 |
книги. Сколько страниц прочитал Юра?
Прежде всего найдём в задаче целое. Это — вся книга и в ней всего 160 страниц.
- 160 : 5 = 32 (стр.) — составляет
1 5 часть страниц.
- Числитель дроби равен 4 , значит взято 4 части.
- 32 · 4 = 128 (стр.) — составляют
4 5 книги.
Оба действия можно записать кратко, в соответствии с правилом нахождения части от целого.

Ответ: Юра прочитал 128 страниц.
Источник: math-prosto.ru
Чему равно 5 в дробях?
Как упростить дроби? Вы можете упростить дробь если числитель (верхнее число) и знаменатель (нижнее число) можно разделить на одно и то же число. Шесть двенадцатых можно упростить до половины или 1 на 2, потому что оба числа делятся на 6. 6 делится на 6 один раз, а 6 на 12 дважды.
Похожие страницы:Блог
Какие есть 3 вида налогов?
Как найти среднюю точку между двумя точками?
Как вы делаете кадровые прогнозы?
Как найти начальную скорость, зная только время?
Что такое 0.05 в виде дроби? Ответ: 0.05 в виде дроби записывается как 1/20.
Во-вторых Чему равна 1/5 в виде дроби? Таблица преобразования десятичных и дробных чисел
| 1/5 | 2/10 | 4/20 |
| 2/5 | 4/10 | 8/20 |
| 3/5 | 6/10 | 12/20 |
| 4/5 | 8/10 | 16/20 |
Какая дробь ближе всего к 25%?
Ответ: 25% можно представить как 1/4 в дробной форме и 0.25 в десятичной форме.
тогда как научить ребенка упрощать дроби?
Как сделать простейшую форму?
Почему мы упрощаем дроби?
Упрощение дробей процесс уменьшения числителя и знаменателя до их наименьших целых чисел, чтобы дробь была в простейшей форме. … Это помогает другим математикам или ученым легко интерпретировать данные, а также помогает избежать путаницы, когда числа и уравнения становятся большими и сложными.
Что такое 0.5 упрощенный? Ответ: 0.5 как дробь записывается как 1/2
Давайте посмотрим, как преобразовать десятичное число в дробь.
Что такое 0.38 в виде дроби?
Объяснение: 0.38 имеет два числа после запятой, поэтому вашей дроби нужны два нуля после единицы в знаменателе (100), а числа после запятой — ваш числитель (38). Таким образом, вы получаете 0.38 =38100 это отменяется, если вы разделите верх и низ на два.
Чему равно 24 в дроби? Примечание. Чтобы превратить десятичную дробь в проценты, просто умножьте ее на 100%. 24100 можно упростить до 625 что является вашей окончательной формой дроби.
Как учить равнозначные дроби семиклассников?
Что такое 1/5 в десятичной системе счисления?
Ответ: 1/5 в виде десятичной дроби выражается как 0.2.
Что такое эквивалентная дробь ks2? Равные дроби две или более фракции, которые все равны. Дробь — это часть целого: знаменатель (нижнее число) показывает, на сколько равных частей разбито целое; числитель (верхнее число) представляет количество этих частей.
Чему равно число 0.25 в виде дроби? Ответ: 0.25 как дробь записывается как 1/4.
Что такое 93% в виде дроби?
Что такое 66.6 повторяющихся процентов в виде дроби? Чему равно 66.6% в виде дроби? 66.6% в виде дроби 66.6/100. Если вы хотите, вы можете упростить его до 333/500. 3.
Почему мы упрощаем дроби для детей?
Слово «упрощать» означает сделать что-то более легким для понимания или выполнения. Таким образом, сокращение или упрощение дробей означает, что мы сделать дробь максимально простой. Мы делаем это, разделив числитель и знаменатель на наибольшее число, которое может точно делиться на оба числа.
Что такое дробь 5-го года? В 5 классе ваш ребенок продолжит изучать дроби как числа, меры и операторы. Теперь они расширят свои знания о дробях до тысячных и начнут изучать проценты. Ключевыми словами в этом разделе являются знаменатель и числитель.
Как упрощаешь дроби 5 класс?
Что является примером простейшей формы? Говорят, что дробь имеет простейшую форму если 1 — единственный общий делитель числителя и знаменателя. Например, 89, потому что 1 — единственный общий множитель 8 и 9 в этой дроби.
Как упростить числа?
Источник: reviews.tn
Мерзляк 5 класс — § 26. Правильные и неправильные дроби. Сравнение дробей

Если числитель дроби равен знаменателю, то дроби равна единице.
2. Какую дробь называют правильной?
Дробь, у которой числитель меньше знаменателя, называют правильной.
3. Какую дробь называют неправильной?
Дробь, у которой числитель больше знаменателя или равен ему, называют неправильной.
4. Какая из двух дробей с равными знаменателями больше? Меньше?
- Из двух дробей одинаковыми знаменателями больше та, у которой числитель больше.
- Из двух дробей с одинаковыми меньше та, у которой числитель меньше.
5. Сравните с единицей любую правильную дробь; любую неправильную дробь.
- Все правильные дроби меньше единицы.
- Все неправильные дроби больше либо равны единице (в случае если числитель равен знаменателю).
6. Сравните любую неправильную дробь с любой правильной дробью.
Каждая неправильная дробь больше любой правильной дроби.
Каждая правильная дробь меньше любой неправильной дроби.
7. Какая из двух дробей с одинаковыми числителями больше? Меньше?
- Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
- Из двух дробей с одинаковыми числителями меньше та, у которой знаменатель больше.
Решаем устно
1. Какую часть составляет:
1) длина стороны квадрата от его периметра
2) секунда от часа
3) угол, градусная мера которого равна 15° от прямого угла
4) угол, градусная мера которого равна 20°, от развёрнутого угла
2. Дима находится в школе с 8 ч 30 мин до 14 ч 30 мин. Какую часть суток Дима проводит в школе?
1) 14 ч 30 мин — 8 ч 30 мин = 6 ч — время, которое Дима проводит в школе.
Ответ: Дима проводит в школе суток.
3. Ваня собрал 35 грибов, из которых составляют белые. Сколько белых грибов собрал Ваня?
35 : 7 • 4 = 5 • 4 = 20 (грибов) — белые.
Ответ: 20 белых грибов.
4. В саду растёт 36 вишнёвых деревьев, что составляет всех деревьев. Сколько деревьев растёт в саду?
36 : 9 • 4 = 6 • 4 = 24 (дерева) — вишнёвые.
Ответ: 24 вишнёвых дерева.
5. Пешеход и велосипедист отправились навстречу друг другу из двух посёлков, расстояние между которыми равно 28 км. Пешеход до встречи прошёл пути. Сколько километров проехал до встречи велосипедист?
1) 28 : 7 • 2 = 2 • 2 = 4 (км) — прошёл пешеход до встречи.
2) 28 — 4 = 24 (км) — проехал велосипедист до встречи.
Упражнения
719. Запишите все правильные дроби со знаменателем 8.
720. Запишите все правильные дроби со знаменателем 11.
721. Запишите все неправильные дроби с числителем 8.
722. Запишите все неправильные дроби с числителем 11.
723. Сравните числа:
724. Сравните числа:
725. Расположите дроби в порядке убывания:
726. Расположите дроби в порядке возрастания:
727. Масса осколка Царь-колокола равна 11 500 кг. Масса царь-колокола составляет — массы этого осколка. Найдите массу Царь-колокола.

1) 11 500 : 23 • 400 = 500 • 400 = 200 000 (кг) — масса Царь-колокола.
Ответ: 200 000 кг.
728. Порция пельменей в кафе «Пампушечка» состоит из 18 пельменей. Иван Гурманов съедает за обедом порции. Сколько пельменей съедает за обедом Иван? На сколько пельменей больше одной порции он съедает?

1) 18 : 9 • 20 = 2 • 20 = 40 (шт) — пельменей съедает Иван Гурманов.
2) 40 — 18 = 22 (шт) — пельменей съедает Иван Гурманов больше одной порции.
Ответ: 40 штук пельменей, на 22 штуки больше одной порции.
729. Найдите все натуральные значения x, при которых дробь будет правильной.
Дробь будет правильной при х = 1, 2, 3, 4, 5, 6, 7, 8.
730. Найдите все натуральные значения х, при которых дробь будет правильной.
Дробь будет правильной при х = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14.
731. Найдите все натуральные значения х, при которых дробь будет неправильной.
Дробь будет неправильной при х = 1, 2, 3, 4, 5, 6.
732. Найдите все натуральные значения х, при которых дробь будет неправильной.
Дробь будет неправильной при х = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13.
733. Найдите все натуральные значения х, при которых выполняется неравенство:
734. Найдите все натуральные значения х, при которых выполняется неравенство:
1) > , при х = 1, 2, 3, 4, 5, 6.
2) > , при х = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
735. Какие цифры можно поставить вместо звёздочки, чтобы:
1) дробь была неправильной
, , — неправильные дроби.
Значит можно подставить вместо звёздочек цифры 7, 8 и 9.
2) дробь была правильной
, — правильные дроби.
Значит можно подставить вместо звёздочек цифры 8 и 9.
736. Найдите все натуральные значения b, при которых дробь будет правильной.
Дробь называют правильной, если числитель дроби меньше, чем её знаменатель.
Такое соотношение возможно, если b = 1, 2, 3, 4.
737. Найдите все натуральные значения b, при которых дробь будет правильной.
Дробь называют неправильной, если числитель дроби больше, чем её знаменатель или если числитель равен знаменателю.
42 ≥ 10 + 4b
42 — 10 ≥ 4b
32 ≥ 4b
Такое соотношение возможно, если b = 1, 2, 3, 4, 5, 6, 7, 8.
738. Найдите все натуральные значения а, при которых:
1) обе дроби и будут правильными
Дробь будет правильной при а = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 и 11.
Дробь будет правильной при а = 8, 9, 10, 11, 12, 13 и т.д.
Значит, обе дроби будут правильными при а = 8, 9, 10 и 11.
Ответ: а = 8, 9, 10 и 11.
2) дробь будет правильной, а дробь — неправильной
Дробь будет правильной при а = 4, 5, 6, 7, 8, 9, 10 и т.д.
Дробь будет неправильной при а = 1, 2, 3, 4, 5 и 6.
Значит, первая дробь будет правильной , а вторая неправильной при а = 4, 5 и 6.
Ответ: а = 4, 5 и 6.
739. Найдите все натуральные значения а, при которых:
1) обе дроби и будут неправильными
Дробь будет неправильной при а = 8, 9, 10, 11, 12, 13, 14, 15 и т.д.
Дробь будет неправильной при а = 1, 2, 3, 4, 5, 6, 7, 8 и 9.
Значит, обе дроби будет неправильными при а = 8 и 9.
2) обе дроби и будут неправильными, а дробь — правильной.
Дробь будет неправильной при а = 10, 11, 12, 13, 14, 15 и т.д.
Дроби будет неправильной при а = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 и 15.
Дробь будет правильной при а = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и 12.
Значит, первые две дроби будет неправильными, а третья дробь правильной при а = 10, 11 и 12.
Ответ: а = 10, 11 и 12.
Упражнения для повторения
740. Объём прямоугольного параллелепипеда равен 180 дм³, а два его измерения — 6 дм и 15 дм. Найдите сумму длин всех рёбер параллелепипеда.
Дано:
a = 6 дм
b = 15 дм
V = 180 дм³
c = ? см
Сумма длин всех рёбер параллелепипеда = ? дм
Решение:
V = abc, значит c = V : (ab)
1) 180 : (6 • 15) = 180 : 90 = 2 (дм) — длина третьего измерения прямоугольного параллелепипеда.
Сумма длин всех рёбер прямоугольного параллелепипеда = 4a + 4b + 4c.
2) 4 • 6 + 4 • 15 + 4 • 2 = 24 + 60 + 8 = 92 (см) — сумма длин всех рёбер прямоугольного параллелепипеда.
741. Из двух городов, расстояние между которыми равно 392 км, выехали одновременно навстречу друг другу два автомобиля. Скорость одного автомобиля равна 48 км/ч, что составляет скорости второго. Какое расстояние будет между автомобилями через 5 ч после начала движения?

1) 48 : 6 • 7 = 8 • 7 = 56 (км/ч) — скорость второго автомобиля.
2) 48 • 5 = 240 (км) — проехал за 5 часов первый автомобиль.
3) 56 • 5 = 280 (км) — проехал за 5 часов второй автомобиль.
4) 240 + 280 = 520 (см) — проехали за 5 часов оба автомобиля.
5) 520 — 392 = 128 (км) — будет расстояние между автомобилями через 5 часов.
Задача от мудрой совы
742. Мартышка, Удав, Слонёнок и Попугай съели вместе 70 бананов, причём каждый из них съел хотя бы один банан. Мартышка съела больше, чем кто-либо из них, Попугай и Слонёнок съели вместе 45 бананов. Сколько бананов съел Удав?
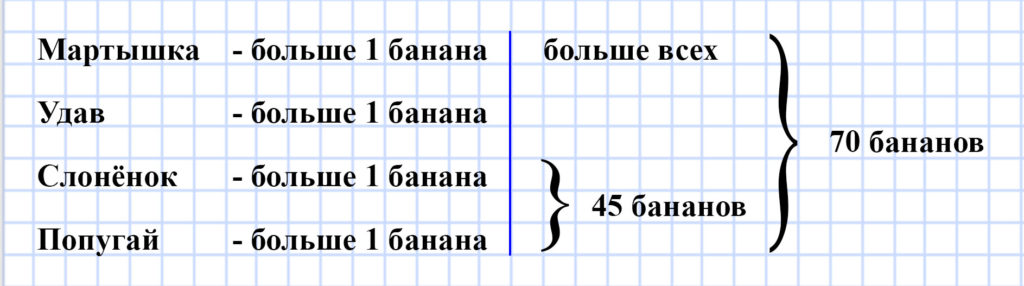
1) 70 — 45 = 25 (бананов) — съели Мартышка и Удав.
2) 25 — 1 = 24 (банана) — самое большое количество бананов, которое могла съесть Мартышка.
И Слонёнок, и Удав, и Попугай съели меньше, чем Мартышка — меньше, чем 24 банана.
Найдём два числа, которые меньше чем 24, и сумма которых равна 45. Единственная пара подходящих чисел — это числа 23 и 22 (23 + 22 = 45).
- Слонёнок съел 22 или 23 банана
- Попугай съел 22 или 23 банана
- Мартышка съела 24 банана — самое большое число
- Удав съел 1 банан (25 — 24 = 1).
Ответ: Удав съел 1 банан.
Источник: matem1234.ru
Обыкновенные дроби простое объяснение для 5 класса: виды, сравнение, сложение, вычитание, умножение, деление.

Каждый школьник, перешагнув первую школьную ступеньку из начальной школы, начинает изучать новый для него материал — дроби. Не смотря на то, что на первый взгляд тема кажется не простой, на самом деле ничего сложного в ней нет, мы постарались ее объяснить доступным языком. Опытные педагоги рекомендуют объяснять ребенку тему дробей и в более раннем возрасте, так как, в повседневной жизни мы постоянно сталкиваемся с дроблением, делением предметов на доли — режем арбуз, торт, пиццу на определенное количество частей, каждая из которых будет частью целого, что и можно записать в виде дроби.
Содержание скрыть
Обыкновенные дроби 5 класс объяснение темы
Если ваш ребенок не понимает тему дробей, очень важно объяснить ему так же, как объясняют в классе и учитывать требования учителя. Детям самим не так просто самостоятельно понять все действия с дробями, задача родителей помочь и привести примеры, которые встречаются каждый день в повседневной жизни. Дайте ребенку шоколадку и попросите отломить от нее часть: целая — это единица, половина — одна вторая, а если плитку разломить на три части, это будет одна треть.
Чтобы лучше понять что такое дробь, нужно запомнить, что это значит — дробить. Когда мы режем торт, каждый кусок будет частью целого торта или очищаем мандарин, каждая долька — это часть целого мандарина. В обоих случаях, это доли целого. Не сложно привести и другие примеры, каждый день мы что-то режем, отделяем.
Арбуз разрезали на 6 частей, каждая часть (доля), это одна шестая от целого плода.

На этой картинке два мандарина. В одном оказалось 6 долек, в другом — 9.

На картинке ниже наглядно видно, как прописываются дроби:

Вот еще пример, желтый круг разрезали на 2 части, это будет одна вторая доли (1/2), зеленый — на 3 (1/3), синий — на 4 (1/4).

Итак, что нужно знать ребенку о дробях?

Чем на меньшее число поделено что-то целое, тем долей больше, а если на большее число, значит они меньше.
Виды обыкновенных дробей
Доли в математике обозначают дробями, называются они — обыкновенные. Для записи используют горизонтальную (-) или наклонную черту (/), например:

Черта между цифрами означает знак деления и может быть заменен на две точки (:) !

Если пиццу разрезать на 6 кусков, а съесть только 2, то дробь вида 2/6 будет означать, что съели 2 куска из 6. В этом случае число «2» будет располагаться над чертой и называется оно «числитель» , а число «6» (под чертой) — «знаменатель», т.е., съели две шестых пиццы.

Далее, нужно понять, сколько кусочков осталось: 6-2=4. Осталось 4 куска, в этом случае дробь выглядит так — 4/6 четыре шестых.
Обыкновенная дробь правильная неправильная
Еще дроби бывают правильными, например те, которые имеют такой вид — 2/8 и неправильными — 8/2 или 8/8. Возьмем неправильную дробь 41/5, читать ее следует так — восемь целых, одна пятая: 8 1/5. Это число называют смешанным, так как в нем отделяются целая часть и дробная. Другими словами мы наглядно видим сколько взяли целых тортов и сколько его частей. Чтобы ребенок осмысленно сокращал дроби, нужно показать ему это на практике и тогда он не будет ошибаться, сокращая дроби.
Для понимания: неправильная дробь трансформируется в целое число, сначала числитель делиться на знаменатель, в результате получается целое число (записывается, как целая часть) и остаток (записывается над чертой) в числитель. Знаменатель, при этом, не меняется.
К неправильным относят и те дроби, числитель и знаменатель которых, имеют одинаковое число, а при делении получается единица — 2/2, 3/3, 4/4 и т.д. Т.е., было взято столько кусков торта, на сколько его поделили.
Наглядно вы можете посмотреть на картинке:

Умножение и деление обыкновенных дробей
Прежде чем приступить к изучению вопроса об умножении и делении дробей, вспомним, что такое натуральные числа? А это те, которые начинаются с единицы — 1 и продолжаться могут до бесконечности. Но, к ним относятся только положительные числа, т.е, со знаком «+». Числа: -1; -2; -3; -4; -5 и т.д., натуральными не являются.
Для того, чтобы совершить действие умножения, нужно умножить числитель одной дроби на числитель другой и, соответственно, перемножить знаменатели. Что у нас получается? В результате вычисления (умножения) мы получаем дробь с числителем, который равен произведению числителей в дробях, и со знаменателем, равным произведению в дробях знаменателей.

Пример:
Умножается число 3 на число 7 (числители). Умножаются знаменатель 5 на знаменатель 10. Записать данное действие можно двумя способами, это вы видите на картинке.

Пример умножения целого числа и дроби:
Целое число (2) записывается в виде дроби (2/1), в которой знаменателем будет единица (1).
![]()

Если нужно произвести деление дробей, поступают следующим образом: умножают первую дробь на перевернутую вторую.

Для простоты восприятия воспользуемся правилом сокращения: делим делитель и знаменатель на одинаковое число, например, дробь 21/63 выглядит не очень хорошо для восприятия, гораздо понятнее будет так — 1/3.

Делим смешанные числа:
Сначала их нужно представить неправильными дробями, затем, разделить друг на друга, вот, что получилось:


Пример:

Обыкновенные дроби сложение вычитание
Правила сложения
Начнем с дробей, у которых одинаковые знаменатели, это самое простое вычисление — высчитывается сумма только числителей — тех чисел, которые находятся над черточкой.
Например:


Можно записать и так:
Немного сложней выполнить действие сложения, если знаменатели разные. В этом случае необходимо сначала:

Пример:

Далее:

Затем, каждую часть дроби, знаменатель и числитель, нужно умножить на свой множитель, который мы определили:

Далее производим сложение дробей:

Правила вычитания
Действие производится аналогичным образом, если у дроби знаменатели одинаковые, необходимо найти разность числителей.

Если у дроби знаменатели разные, Так же, как и при сложении, находим наименьшее кратное число.
 Сравнение дробей 5 класс
Сравнение дробей 5 класс
Прежде всего необходимо обратить внимание на их знаменатели, если они одинаковые, меньше будет та, чей числитель больше.
Пример:

А если числительные одинаковые, меньше та, чей знаменатель больше.
Пример:

Сложнее обстоит дело, если знаменатели разные. В этом случае сначала определяем общий знаменатель (под чертой) и приводим к нему обе дроби.
Пример:

Далее получаем:

Сравниваем:

Запомните!

P.S. Итак, мы рассмотрели одну из тем по математики для 5 класса. Ее необходимо знать, чтобы ребенок смог двигаться дальше и изучать более сложный материал.
Для лучшего понимания покажите ребенку видео.

Источник: vsetemi.ru
Неправильные дроби — примеры для 5 класса с решением и объяснением

Математика — это не просто цифры. С её помощью познаётся окружающий мир. Умение работать с числами позволяет прогрессировать всему человечеству. Особое положение занимает раздел, изучающий действия с дробными отношениями. Именно с ними приходится чаще всего встречаться в жизни. Поэтому нужно пристальное внимание обратить в 5 классе на неправильные дроби.
Примеры с объяснением помогут лучше разобраться в теме и построят важный мост для дальнейшего изучения науки.
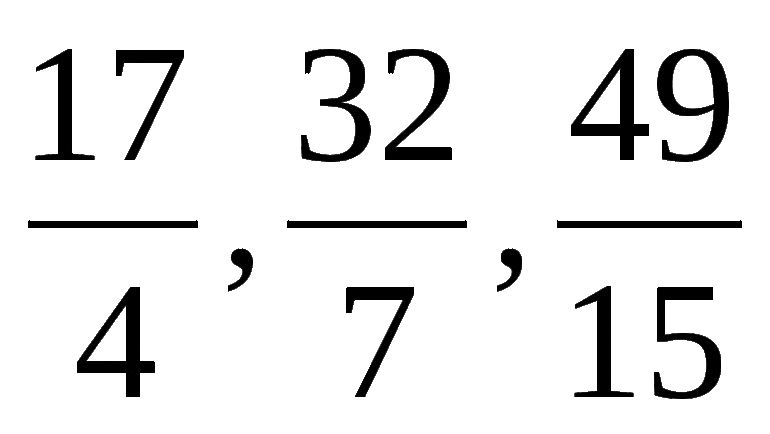
Общие сведения
Слово «дробь» в обиход ввёл математик средневековой Европы Фибоначчи. На Руси под этим понятием понимались доли чисел. В дословном переводе на русский с арабского термин обозначает «ломать» или «раздроблять». Вид записи выражения, который применяется и сегодня, предложили арабы. Но фундамент теории заложили греческие и индийские учёные.
В математике под дробным отношением понимают число, образованное из некоторой части единицы. Простыми словами это можно объяснить на наглядном примере. Пусть на столе лежит две круглые пиццы. Каждую из них разрезали на восемь равных частей. Всего получилось шестнадцать долей.
Через какое-то время было съедено одиннадцать кусков. Соответственно на столе осталось пять. В математической записи такое действие будет выглядеть как 11 / 8. Это легко проверить: 11/ 8 пиццы — это тоже что 8 / 8 плюс 3 / 8. То есть одна была полностью съедена, а с другой взяли только три кусочка. Так как отношение 8 / 8 — это целое (единица), то можно утверждать, что 8 / 8 = 1. Значит, произошедшее можно представить в виде равенства: 11 / 8 = 1 + 3 / 8.
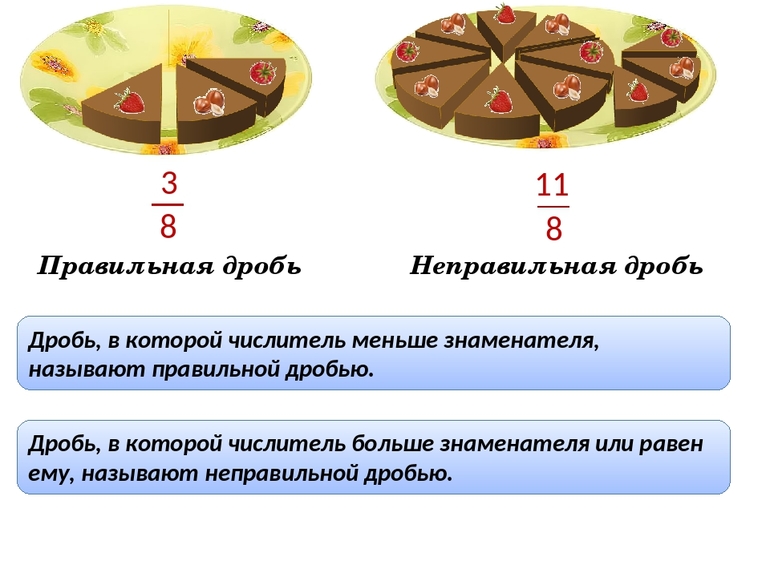
- Правильные. Рациональные выражения, в которых числитель меньше или неравен делителю. Например, 1 / 16; 4 / 45; -78 / 123.
- Неправильные. Обыкновенные дроби, у которых знаменатель количественно меньше значения делимого или равен ему по численности. Например, 7 / 6; 19 / 19; 453 / 21.
- Смешанные. Отношения, включающие в свою запись как натуральное число, так и правильную дробь. Фактически они представляют собой их сумму: 4 (4 / 5) = 4 + 4 / 5
Кроме этого, выделяют ещё одну группу выражений. Дроби, относящиеся к ней, называют десятичными. Это такие отношения, у которых знаменатель — это десятичное число, стоящее в любой натуральной степени. Для записи десятичных выражений используют не дробную черту, а запятую. Например, 12 / 10 = 1,2.
Так как, по сути, дроби — это числа, только чаще всего не целые, над ними можно выполнять любые операции. Для того чтобы школьника научить правильно решать дроби, в 5 классе, кроме теоретического материала несколько уроков уделяют практике. На ней, кроме непосредственного выполнения арифметических операций, учат преобразовывать дробные отношения из одного вида в другой.
Суть отношения
Обыкновенная дробь может быть правильной или неправильной. Например, 19 / 21 — правильное выражение, так как результат деления будет меньше единицы. В то же время обыкновенные числа 32 / 6 и 90 / 90 — неправильные, так как ответ, получаемый при делении, будет больше единицы в первом случае и равен ей во втором.
Чтобы разобраться, почему же дробные выражения, у которых числитель превосходит или равняется знаменателю называют «неправильными» можно порассуждать следующим образом.
Пусть имеется неправильная дробь 10 / 10. Эта запись обозначает, что взято десять долей чего-то состоящего из такого же числа частей. Иными словами, из имеющихся десяти долей можно сложить целый предмет. Неправильное выражение вида 10 / 10, по сути, означает целый предмет. Значит, можно записать, что 10 / 10 =1.
Следовательно, такое отношение можно заменить натуральным числом.
Теперь можно рассмотреть неправильные отношения 7 / 3 и 12 / 4. Совершенно очевидно, что из этих семи третьих долей легко составляется два целых числа. Одно из них будет содержать три части. Значит, для оставшихся двух долей понадобится шесть частей: 3 + 3 = 6. При этом останется ещё одна доля — третья. Таким образом, выражение семь третьих означает две целые части и ещё одну третью от них.
Аналогично из двенадцати четвёртых можно сформировать три целых числа по четыре доли в каждом. То есть дробное отношение 12 / 4 означает, по сути, три целых предмета.
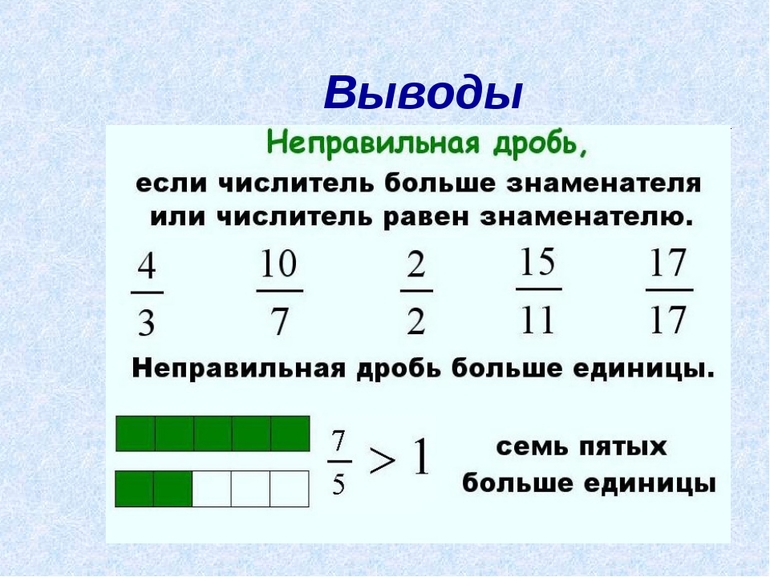
Если провести анализ полученных результатов, то можно сделать вывод о том, что неправильные дроби, могут быть представлены в двух видах:
- натуральным числом — в случае когда числитель количественно совпадает со знаменателем;
- суммой правильной дроби и простого числа — если делимое не делится нацело на делитель.
Как и любое число, дробь может быть положительной и отрицательной. В первом случае она обозначает изменение чего-то в сторону увеличения, а во втором — уменьшения. Например, -6 / 5 может обозначать недостачу равную шесть пятых.
Особенный интерес вызывает представление неправильной дроби в виде суммы натурального числа и правильной части. Это действие называется выделением целой доли из неправильного отношения. Причём такая операция может быть выполнена и в обратном направлении — трансформация выражения в смешанное.
Превращение дробей
По смыслу неправильные выражения представляют собой целую и дробную часть, записанную в виде отношения. Поэтому любую смешанную дробь можно превратить в правильную, и наоборот. Деление целого числа на такое же можно объяснить так. Пусть нужно разделить четыре на пять.
Значит, единицу понадобится разделить на пять равных частей, то есть 1 / 5. Четыре же единицы дадут 1 / 5 + 1/ 5 + 1 / 5 + 1 / 5 = 4 / 5. В этом случае получается правильное выражение. Но бывает, что числитель количественно превышает знаменатель. Значит, для более понятной формы записи нужно из такого выражения выделить целую часть.

Например, нужно преобразовать число 25 / 8. Это действие подразумевает нахождение целых единиц, содержащихся в выражении. Рассуждать нужно следующим образом. Одна единица может быть представлена как 8 / 8, две — 16 / 8, три — 24 / 8. Значит, число состоит из трёх единиц и оставшейся 1 / 8 части. Поэтому записать его можно так: 3 (1 / 8).
Поняв смысл такого перехода, можно выполнить превращение и в обратную сторону. Чтобы разобраться, как это сделать лучше, проще рассмотреть пример. Пусть имеется смешанное число 4 (5/8), его нужно превратить в неправильную дробь. Иными словами, определить, сколько восьмых долей содержится в четырёх и пяти восьмых. Так как одной единице соответствует 8 / 8, то четырём — 8 * 4 / 8 = 32 / 8. Соответственно в четырёх и 5 / 8 будет 37 / 8 долей.
Такого вида преобразования часто приходится выполнять при решении примеров с дробями в 5 классе. Поэтому понять принцип превращения лучше всего на конкретное задание. При этом можно использовать следующий алгоритм:
- перемножить единицы целой части со знаменателем дробного числа;
- сложить полученное произведение и числитель дроби;
- результат сложения записать в числитель, а знаменатель оставить без изменений.

Итак, пусть имеется выражение 3 (5 / 7). Так как фактически это сумма трёх и пяти седьмых, то следуя алгоритму, можно решение расписать так: 3 + 5 / 7 = (3 * 7 + 5) / 7 = (21 + 5) / 7 = 26 / 7. Аналогичный результат мог быть получен при простом сложении двух частей смешанного числа: 3 / 1 + 5 / 7 = (3 * 7) / 1 * 7 + 5 / 7 = 21 / 7 + 5 / 7 = (21 + 5) / 7 = 26 / 7. Первый вариант, конечно же, более удобен. Его можно выразить формулой: a (c / d) = (a * d + c) / d.
Эту выражение нужно обязательно запомнить, так как его придётся довольно часто использовать при решении задач различной сложности.
Выполнение действий
Отличие неправильной дроби от правильной заключается в том, что первая равна или больше единицы, а вторая меньше её. Поэтому правило выполнения арифметических действий одинаковое для этих двух групп. Для того чтобы ребёнок понял, как правильно решать простые и сложные задания объяснение в 5 классе неправильных дробей и действий над ними начинают с повторения правила разложения числа на простые множители.
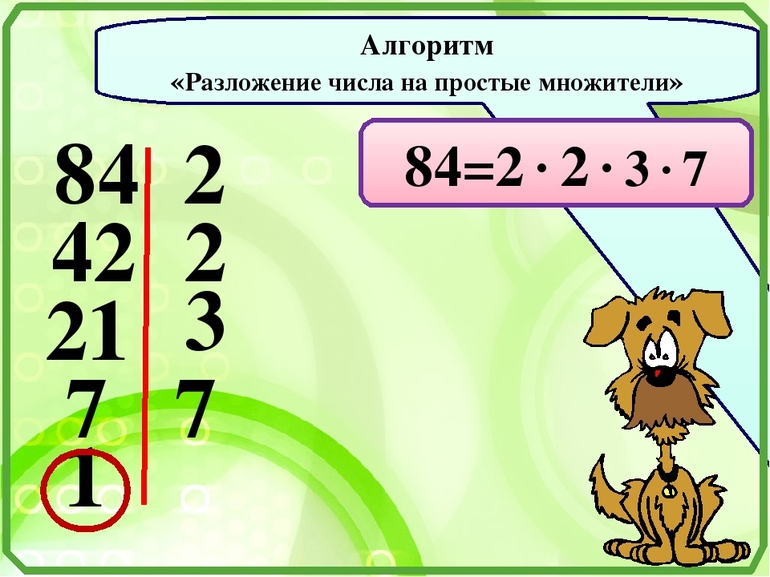
Выполняется оно за несколько шагов. Вначале ищут минимальную величину, на которую можно разделить исходное без остатка. Далее, находят результат деления и повторяют действие, но уже для полученного числа. Операцию повторяют до тех пор, пока в ответе не получится единица.
Разложение на простые множители используется при поиске наименьшего знаменателя при сложении или вычитании неправильных дробей с разными делителями. Существует алгоритм, придерживаясь которого можно выполнить любое арифметическое действие над двумя и более дробными выражениями. Он заключается в следующем:
- исследовать числитель и знаменатель на возможность сокращения;
- определить наименьший общий знаменатель (НОЗ) среди делителей;
- найти дополнительные множители;
- выполнить умножение числителей на найденные аргументы;
- в знаменатель записать НОЗ, а в числитель сумму или разность произведений делимых.
Например, 4 / 3 + 9 / 7 = (7 * 4) / 21 + (3 * 9) / 21 = 28 / 21 + 27 / 21 = (28 + 27) / 21 = 55 / 21 = 2 (13 / 21) и 56 / 9 — 6 / 9 = (56 — 6) / 9 = 50 / 9 = 5 (5 / 9).

Неправильные выражения можно не только складывать, но и вычитать. Для того чтобы их перемножить следует отдельно найти произведение делимых и делителей. Затем в числитель записать первый результат, а в знаменатель второй. То есть действие нужно выполнять по формуле: f / n * s / m = (f * s) / (n * m). Выполнить деление также просто.
Для этого действия в вычитаемом выражении меняется местами аргументы и выполняется умножение: (f / n) / (s / m) = (f * m) / (n * s).
Возведение в степень и извлечение корня выполняют способом разделения. То есть, делимое от делителя возводится или извлекается отдельно: (s / m) j = s j / m j и √(s / m) = √s / √m. Например, 3 / 2 * 9 / 6 : 7 / 5 * (3 / 2) 3 . С какого действия начинать решение не принципиально, но следует обратить внимание, что 9 / 6 можно сократить на три. В итоге получится 9 / 6 = 3 / 2. Далее, решение будет выглядеть следующим образом: 3 / 2 * 3 / 2 : 7 / 5 * 3 3 / 2 3 = (3 * 3) / (2 * 2): 7 / 5 * 27 / 8 = 9 / 4 * 5 / 7 * 27 / 8 = (9 * 5 * 27) / (4* 7 * 8) = 1215 / 224 = 5 (95 / 224).
Источник: nauka.club