
Согласно учебной программе по математикедети должны научиться решать задачи на движение еще в начальной школе. Однако задачи такого вида часто вызывают уучащихся затруднение. Важно,чтоб ребенок понял, что такое собственная скорость, скорость течения, скорость по течению и скорость против течения. Только при этом условии школьник сможет легко решать задачина движение.Вам понадобится
Собственная — это скорость катера или другого средства передвижения в неподвижной воде. Обозначьте ее — V собств.
Вода в реке находится в движении. Значит она имеет свою скорость, которая называется скоростью течения (V теч.)
Скорость катера по течению реки обозначьте — V по теч., а скорость против течения — V пр. теч.
Теперь запомните формулы, необходимые для решения задач на движение:
V пр. теч.= V собств. — V теч.
V по теч.= V собств. + V теч.
Как найти собственную скорость лодки и реки, зная скорость по течению и против течения реки. 5-6 кл.
Итак, исходя из этих формул, можно сделать следующие выводы.
Если катер движется против течения реки, то V собств. = V пр. теч. + V теч.
Если катер движется по течению, то V собств. = V по теч. — V теч.
Решим несколько задач на движение по реке.
Задача 1. Скорость катера против течения реки 12,1 км/ч. Найдите собственную скорость катера, зная , что скорость течения реки 2 км/ч.
Решение: 12,1 + 2 = 14, 1 (км/ч) — собственная скорость катера.
Задача 2. Скорость катера по течению реки 16,3 км/ч, скорость течения реки 1,9 км/ч. Сколько метров прошел бы это катер за 1 мин., если находился в стоячей воде?
Решение: 16,3 — 1,9 = 14,4 (км/ч) — собственная скорость катера. Переведем км/ч в м/мин: 14,4 / 0,06 = 240 (м/мин.). Значит, за 1 минуту катер прошел бы 240 м.
Задача 3. Два катера отправились одновременно навстречу друг другу из двух пунктов. Первый катер двигался по течению реки, а второй — против течения. Встретились они через три часа. За это время первый катер прошел 42 км, а второй — 39 км.Найдите собственную скорость каждого катера, если известно, что скорость течения реки 2 км/ч.
Решение: 1) 42 / 3 = 14 (км/ч) — скорость движения по течению реки первого катера.
2) 39 / 3 = 13 (км/ч) — скорость движения против течения реки второго катера.
3) 14 — 2 = 12 (км/ч) — собственная скорость первого катера.
4) 13 + 2 = 15 (км/ч) — собственная скорость второго катера.
Источник: completerepair.ru
Что такое собственная скорость лодки по математике
Собственная скорость лодки является одной из важнейших характеристик, определяющих ее маневренность и проходимость. В отличие от скорости судна, которая измеряется относительно земной поверхности и зависит от ее состояния, этот показатель позволяет оценить, как быстро лодка движется относительно воды. Точное определение этой величины является задачей математики и физики, и требует учета многих факторов, таких как вес лодки, ее габаритные размеры и форму корпуса.
В данной статье мы рассмотрим основные методы определения собственной скорости лодки, а также приведем примеры расчетов для различных типов судов. Мы также рассмотрим основные принципы, которыми руководствуются специальные программы и калькуляторы для определения данной характеристики.
Если вы являетесь любителем или профессионалом морской навигации, то в данной статье вы найдете много полезной информации о том, как правильно определять собственную скорость своей лодки, и как это может повлиять на ее работу и проходимость на воде.
Собственная скорость лодки по математике: определение и расчеты
Собственная скорость лодки — это скорость, с которой лодка может двигаться без помощи внешних сил, например, без помощи ветра или течения. Она является важной характеристикой любой лодки и может быть рассчитана по формуле:
v0 = (l * √(g * ρ)) / (12 * ῥ)
- v0 — собственная скорость лодки в метрах в секунду
- l — длина лодки в метрах
- g — ускорение свободного падения (9,81 м/с²)
- ρ — плотность воды (обычно принимается 1000 кг/м³)
- ῥ — отношение массы лодки к объему, выраженное в кг/м³ (обычно принимается 1000 кг/м³)
Например, у нас есть лодка длиной 5 метров и массой 500 кг. Примем, что плотность воды равна 1000 кг/м³:
- Вычисляем объем лодки: V = l * w * h = 5 * 2 * 1 = 10 м³
- Вычисляем отношение массы к объему: ρ = масса / объем = 500 / 10 = 50 кг/м³
- Подставляем известные значения в формулу: v0 = (5 * √(9,81 * 1000)) / (12 * 50) ≈ 1,85 м/с
Таким образом, мы рассчитали, что собственная скорость данной лодки без использования внешних сил составляет около 1,85 м/с.
Что такое собственная скорость лодки?
Собственная скорость лодки – это скорость, которую может развить лодка, двигаясь без попутного ветра и без течения, при полностью работающем двигателе и оптимальном загрузе.
Таким образом, собственная скорость лодки зависит от ряда факторов, таких как конструктивные особенности судна, мощность и тип двигателя, размер и форма корпуса, масса и распределение груза.
Для расчета собственной скорости используются специальные формулы, учитывающие все вышеперечисленные факторы. Эти формулы позволяют определить наилучшую скорость, которую может развить лодка в определенных условиях.
Знание собственной скорости лодки необходимо для правильного выбора маршрута, определения расхода топлива и предотвращения возможных аварийных ситуаций.
Формула расчета собственной скорости лодки
Для определения собственной скорости лодки необходимо использовать некоторые математические формулы и данные о лодке.
Формула для расчета собственной скорости:
- V — собственная скорость лодки в узлах
- k — коэффициент сопротивления лодки воде
- d — напорная высота лодки
Для расчета k и d можно использовать следующие формулы:
Формула для расчета коэффициента сопротивления:
- U — скорость лодки в узлах
- L — длина водолазной части лодки в метрах
Формула для расчета напорной высоты:
- T — тяга на винте лодки в ньютонах
- ρ — плотность воды в кг/м^3
- g — ускорение свободного падения в м/с^2
- d — диаметр винта в метрах
Используя эти формулы, можно определить собственную скорость лодки, что является важной характеристикой при выборе судна для плавания.
Примеры расчета собственной скорости лодки по математике
Для расчета скорости лодки необходимо знать ее габариты и свойства воды, в которой она будет двигаться. Например, пусть имеется лодка длиной 5 метров и шириной 2 метра, движущаяся по реке с течением скоростью 3 км/час. Среднее значение скорости лодки по течению и против течения приблизительно равно 4 км/час.
Получим значение Froude Number для лодки, который показывает, насколько сильно волны будут влиять на движение лодки. Для этого нужно найти скорость лодки в метрах в секунду и поделить ее на корень квадратный из произведения длины лодки на ускорение свободного падения. Для лодки длиной 5 метров скорость будет равна 4/3.6=1.11 м/с.
Froude Number для данной лодки равен 0.28, и это показывает, что на скорость лодки будут оказывать влияние волны, но не слишком сильно. Используя формулу Стрибека, можно определить максимальную скорость лодки: V = (1.34 * L * √(g * B)) / Froude Number, где L — длина лодки, B — ее ширина, g — ускорение свободного падения. Получаем значение 5.76 м/с, что равно примерно 20.7 км/час.
В зависимости от размера, формы и других параметров лодки, скорость может сильно варьироваться. Однако, математический расчет позволяет предвидеть и спрогнозировать наиболее эффективную скорость, при которой лодка будет двигаться наиболее оптимально под заданными условиями.
Вопрос-ответ
Как узнать скорость лодки по математике?
Для определения собственной скорости лодки по математике нужно знать только два параметра: массу лодки (в килограммах) и мощность двигателя (в лошадиных силах). Формула расчета: V = (P * 735.5) / m, где V — скорость лодки в км/ч, Р — мощность двигателя в лошадиных силах, m — масса лодки в кг. Например, если масса лодки равна 300 кг, а мощность двигателя — 40 л.с., то скорость лодки будет V = (40 * 735.5) / 300 = 98,2 км/ч.
Влияет ли на скорость лодки ее форма и размеры?
Да, форма и размеры лодки могут значительно влиять на ее скорость. Лодки с узкими корпусами обычно имеют меньшее сопротивление воды и высокую скорость, чем широкие лодки с большим объемом. Размеры лодки также влияют на ее скорость, потому что большие лодки требуют более мощных двигателей, чтобы достичь той же скорости, что и меньшие лодки.
Как поддерживать максимальную скорость лодки?
Чтобы поддерживать максимальную скорость лодки, нужно учитывать несколько факторов. Сначала следует правильно выбрать двигатель, чтобы он соответствовал массе лодки и требуемому уровню скорости. Затем нужно правильно загрузить лодку, чтобы она была сбалансирована и не имела излишнего веса. Также важно регулярно проводить техническое обслуживание двигателя и проверять его работоспособность. Кроме того, нужно следить за погодными условиями и избегать экстремальных условий, таких как сильный ветер, грозы и высокие волны.
Источник: psk-group.su
Задача о лодке и течении

Теченьем лодку уносило.
Я зацепиться чудом смог.
За борт держась, собравшись с силой,
Залез в неё, на днище лёг.
— Король и Шут. «Утопленник».
Постановка задачи
Лодка шла по течению со скоростью 12,6 км/ч, а против течения — со скоростью 8,8 км/ч. Найдите скорость течения, зная, что собственная скорость лодки не изменялась.
Демагогия
Вот как: «шла по течению». Реверанс в сторону судоходного сленга?
Почему-то не уточняется: изменилась ли скорость течения реки. Откуда читателю знать, что оба эксперимента проведены в один сезон? Иными словами, допускается, что время между двумя экспериментами столь мало, что в системе не появились дополнительные эффекты, а потому правомочно описывать оба события, как события происходящие одновременно, но не влияющие друг на друга.
Терминология
Чтобы избежать дальнейших кривотолков, как это и положено, уточним терминологию. В данной задаче слишком уж много скоростей для двух предложений. В дальнейшем будем разделять следующие понятия. Собственная скорость лодки vл.с., то есть скорость, которую судно приобретает на спокойной (неподвижной) воде благодаря специальному устройству (парус, двигатель).
Скорость лодки относительно берега vл.бер., то есть скорость, с которой лодка движется для стоящего на берегу наблюдателя (это движение может быть вызвано одним лишь течением реки, а может и являться суперпозицией воздействий среды и собственного движителя лодки).
Решение
На первый взгляд, всё кажется элементарным. Сначала лодка плывёт по течению, приобретая дополнительную скорость благодаря водной среде, затем — против течения, противоборствуя, и теряя скорость. И вот тут — сюрприз.
Вспомните, как в метро, часть пассажиров идёт по движущемуся эскалатору, выигрывая дополнительные секунды.
А теперь, представьте себе покупателя в торговом центре, очень спешащего на распродажу (открытие нового магазина). На пути шопоглика — эскалаторы, но, опьянённый скидками, покупатель выбирает эскалатор не с тем направлением движения полотна, и начинается состязание в упорстве. Зная тяжесть ониомании, можно предположить не только ситуацию, когда эскалатор увлекает человека вместе с собой, но и когда человек, идёт наперекор аппарату, титаническим усилием преодолевая его путы.
К чему это отступление? С математической точки зрения, модель движения человека на эскалаторе (ещё точнее — на траволаторе) и модель движения лодки по реке — идентичны. Теперь, вернёмся к лодкам.
Читаем задачу, попутно строя модель происходящего:
Лодка шла по течению со скоростью 12,6 км/ч
Ну, тут всё понятно: сложение скоростей:
vтеч+vл.с.=12,6 км/ч
против течения — со скоростью 8,8 км/ч
Ну, а тут — вычитание скоростей. И сразу же учащийся уточняет: что из чего вычитать?
Кажущийся, чисто синтаксическим вопрос, имеет, ожидаемо, семантическую интерпретацию. Вспоминая, шопоголика на эскалаторе, мы должны определиться: поплывёт ли лодка к цели против течения, или усилий её движителя не хватит и она будет покорно уносится течением от заветной цели всё далее и далее?
Чтобы стало совсем понятно, я набросал схемку (надеюсь, у Вас цветной монитор):
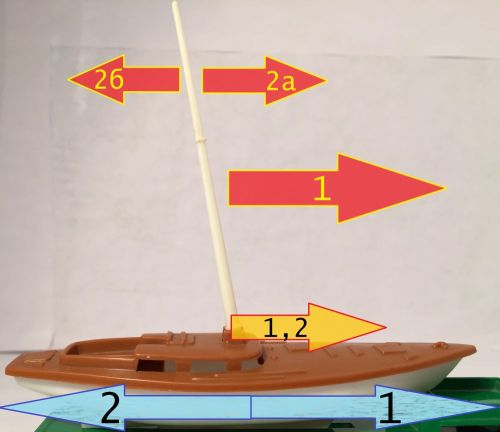
Ситуация 1. Течение реки (1, голубая стрелка) совпадает с движением лодки (1, оранжевая стрелка). Результирующее движение (1, красная стрелка) ожидаемо имеет ориентацию «вперёд».
Ситуация 2. Течение реки (2, голубая стрелка) не совпадает с движением лодки (2, оранжевая стрелка). Результирующее движение имеет ориентацию «вперёд» (2а, красная стрелка) или «назад» (2б, красная стрелка). Оба исхода не противоречат определению vл.бер., которое мы сформулировали ранее.
Итоговое направление определяется соотношением скорости течения и собственной скорости лодки. Но мы не знаем этих величин!
Как это получилось?
«Что за ерунда?! Аналогичные задачки про два автомобиля решались однозначно!» Если Вы внимательно читали мою заметку про два автомобиля, то должны были усвоить тезисы (по крайней мере — я старался это показать):
- Отсутствие аппарата отрицательных чисел приводит к необходимости принятия индивидуального решения для конкретных значений скоростей (невозможно априорно синтезировать алгоритм решения без ветвлений).
Здесь же автор задачи говорит просто о «скорости», подразумевая, очевидность направления результирующего движения лодки.
Корректное решение
Теперь, понимая, что в задаче говорится о модуле скорости, мы можем записать систему уравнений целиком:
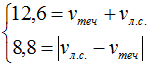
Единственный способ аналитически вытащить выражение из-под знака модуля — рассмотреть два несовместных события:
- Число под знаком модуля положительно — оставляем исходное выражение.

Рассмотрим решение двух несовместных систем:
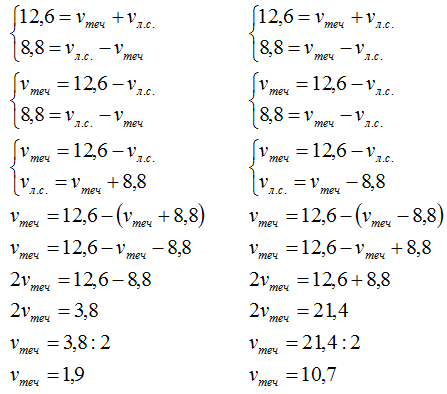
Внимание: правильный ответ
В учебнике, ожидаемо, указан лишь один правильный ответ. Аналогичная ситуация и на сайтах с решениями задач.
У этой задачи, в виду дефицита (неполноты) предоставленной информации, два варианта правильного ответа.
Ответ из учебника соответствует шаблонной ситуации: сначала лодка летит по волнам вместе с течением (vл.бер.=1,9+10,7=12,6), затем, слегка теряя в скорости (vл.бер.=10,7-1,9=8,8), уверенно покоряет реку в обратном направлении.
Второй ответ (который привожу я) повествует о лодке, сначала ускоренной течением полноводной реки (vл.бер.=10,7+1,9=12,6), затем — тщетно пытающейся преодолеть стихию (vл.бер.=10,7-1,9=8,8).
Таким образом, в данной формулировке, задача допускает два варианта ответа:
vтеч=1,9 км/ч и vтеч=10,7 км/ч
Где все?
Большинство людей — оптимисты (ну или просто — шаблонно мыслят): в их сознании, фраза «против течения» автоматически трансформируются в картину мужественного преодоления стихии. В общем же случае, допустима ситуация, в которой борьба с течением может всего лишь позволить выиграть время, но не приблизить к цели ни на йоту.
И не надо меня уверять, что ситуация лишена смысла: данный манёвр (дрейф) можно оправдать различными ситуациями. Добавлю к этому: в задаче сказано, что скорость лодки не менялась в рамках указанных заплывов, но не сказано, что это единственно доступный скоростной режим (возможно, спустя некоторое время, собственная скорость будет увеличена и лодка покорит течение).
Что делать?
- Похвалить учащегося за умение ставить правильные вопросы.
Источник: nabatchikov.com