При стрельбе из одного и того же оружия при самом тщательном соблюдении точности и однообразия производства выстрелов каждая пуля вследствие ряда случайных причин описывает свою траекторию и имеет свою точку падения (точку встречи), не совпадающую с другими, вследствие чего происходит разбрасывание пуль.
Явление разбрасывания пуль при стрельбе из одного и того же оружия в практически одинаковых условиях называется естественным рассеиванием пуль, или рассеиванием траекторий.
Точка пересечения средней траектории с поверхностью цели (преграды) называется средней точкой попадания, или центром рассеивания.
Площадь, на которой располагаются точки встречи (пробоины) пуль, полученные при пересечении снопа траекторий с какой-либо плоскостью, называется площадью рассеивания.
Площадь рассеивания обычно имеет форму эллипса. При стрельбе из стрелкового оружия на близкие расстояния площадь рассеивания в вертикальной плоскости может иметь форму круга.
Взаимно перпендикулярные линии, проведенные через центр рассеивания (среднюю точку попадания) так, чтобы одна из них совпадала с направлением стрельбы, называются осями рассеивания.
Кратчайшие расстояния от точек встречи (пробоин) до осей рассеивания называются отклонениями.
Источник: m.studref.com
Средняя точка попадания
Средняя точка попадания или средняя точка прицеливанния (СТП) — термин, имеющий отношение к прикладной баллистике и количественному определению меткости стрельбы. Обозначает геометрический центр эллипса рассеивания метательных снарядов при стрельбе по мишени.
Определение
Очевидно, что даже при ведении огня из совершенно исправного оружия на динамику полёта снарядов к цели влияет множество разных случайных факторов, например:
- разброс значений в массогабаритных параметрах снарядов влияет на начальную скорость каждого снаряда, которая в свою очередь влияет на настильность его траектории.
- в случае огнестрельного оружия на начальной скорости пули также сказываются качество и состав пороха, капсюльного воспламеняющего состава, качество крепления пули в горлышке гильзы и т.д.
- разброс в геометрической форме и размерах метательных снарядов определяет колебания аэродинамического сопротивления при полёте к цели
- случайные и систематические (ветер) возмущения среды, в которой двигается снаряд также сказываются на рассеянии
- и т.д.
Таким образом формируется так называемый эллипс рассеивания, центром которого является средняя точка попадания [1] . Так как влияние вышеназванных причин невозможно предсказать, то меткость стрельбы предпочитают описывать положением центра эллипса рассеивания относительно желаемой точки попадания (центра мишени). Геометрические размеры эллипса позволяют описать кучность стрельбы.
Методы определения
В случае малого количества попаданий (от двух до четырех) положение средней точки попадания определяется как простое среднее. При большом количестве снарядов наиболее простым методом оценки положения средней точки попадания является определение горизонтальной и вертикальной линий, по обоим сторонам которых располагается одинаковое количество пробоин. Их пересечение и дает среднюю точку попадания [2] .
Примечания
- ↑Естественное рассеивание выстрелов (Разброс). Средняя точка попадания
- ↑Статья «Проверка и пристрелка нарезного оружия» на сайте www.hunter.ru
Литература
- Монетчиков С.Рассеивание пуль при стрельбе // Братишка : Ежемесячный журнал подразделений специального назначения. — М .: ООО «Витязь-Братишка», 2010. —. —.
Ссылки
Источник: wp.wiki-wiki.ru
Способы определения положения средней точки попадания
Способы определения положения средней точки попадания
Определение положения средней точки попадания способом последовательного деления отрезков: а — по трем; б и в — по четырем; г — по пяти пробоинам При малом числе пробоин (до 5) положение средней точки попадания определяется способом последовательного деления отрезков.
Для этого необходимо: — соединить прямой две пробоины (точки встречи) и расстояние между ними разделить пополам; — полученную точку соединить с третьей пробоиной (точкой встречи) и расстояние между ними разделить на три равные части; так как к центру рассеивания пробоины (точки встречи) располагаются гуще, то за среднюю точку попадания трех пробоин (точек встречи) принимается деление, ближайшее к двум первым пробоинам (точкам встречи);
Определение положения средней точки попадания способом проведения осей рассеивания: ВВ1 — ось рассеивания по высоте; ББ1 — ось рассеивания по боковому направлению — найденную среднюю точку попадания для трех пробоин (точек встречи) соединить с четвертой пробоиной (точкой встречи) и расстояние между ними разделить на четыре равные части; деление, ближайшее к первым трем пробоинам (точкам встречи), принимается за среднюю точку попадания четырех пробоин (точек встречи).
По четырем пробоинам (точкам встречи) среднюю точку попадания можно определить еще так: рядом лежащие пробоины (точки встречи) соединить попарно, середины обеих прямых снова соединить и полученную линию разделить пополам; точка деления и будет средней точкой попадания.
При наличии пяти пробоин (точек встречи) средняя точка попадания для них определяется подобным же образом.
При большом числе пробоин (точек встречи) на основании симметричности рассеивания средняя точка попадания определяется способом проведения осей рассеивания.
Для этого нужно: — отсчитать нижнюю (ближнюю) половину пробоин (точек встречи) и отделить ее осью рассеивания по высоте (дальности); — отсчитать таким же порядком правую или левую половину пробоин (точек встречи) и отделить ее осью рассеивания по боковому направлению; — пересечение осей рассеивания является средней точкой попадания.
Среднюю точку попадания можно также определить способом вычисления (расчета). Для этого необходимо:
| Пробоин | Расстояние в см от пробоин до | |
| вертикальной линии | горизонтальной пинии | |
| 1 | 13 | 52 |
| 2 | 3 | 44 |
| 3 | 0 | 35 |
| 4 | 27 | 39 |
| 5 | 8 | 27 |
| 6 | 17 | 33 |
| 7 | 20 | 22 |
| 8 | 3 | 13 |
| 9 | 35 | 15 |
| 10 | 24 | 0 |
| Сумма делённая на число пробоин | ||
Определение положения средней точки попадания способом вычисления (расчета)
— провести через левую (правую) пробоину (точку встречи) вертикальную линию, измерить кратчайшее расстояние от каждой пробоины (точки встречи) до этой линии, сложить все расстояния от вертикальной линии и разделить сумму на число пробоин (точек встречи); — провести через нижнюю (верхнюю) пробоину (точку встречи) горизонтальную линию, измерить кратчайшее расстояние от каждой пробоины (точки встречи) до этой линии, сложить все расстояния от горизонтальной линии и разделить сумму на число пробоин(точек встречи).
Полученные числа определяют удаление средней точки попадания от указанных линий.
Теги: огневая подготовка
Пристрелка АК, АКМ, АКСУ. Баллистика и СТП.
Пристрелка АК, АКМ, АКСУ и т.п. Баллистика и средняя точка попадания (СТП).
Предлагаем в этой публикации обсудить варианты пристрелки, приведения к нормальному бою карабинов на базе АК. От себя приводим свой вариант пристрелки на 300 метров.
АКМ калибр 7.62х39. Стреляем с упора. Сидя. Высота стола около 1 м. Мишени висят на дистанции 100 метров на высоте около 1.5 метра. Методика пристрелки на базе «Наставление по стрелковому делу, 7.62-мм модернизированный АК (АКМ и АКМС) – 1983».
С учётом того, что в прикладной и практической стрельбе, для карабина максимальная рекомендуемая дистанция до мишени 300 метров, то при такой пристрелке можно спокойно поражать мишени на 300 метров с прицелом «П» или что тоже самое «3», а ближние стрелять или с теми же прицелами внося поправки на глаз, или же переключаться на прицел «1». Почему мы именно за пристрелку на 300 метров и стрельбы с прицела «П» (3), можно понять если взглянуть на таблицу «ПРЕВЫШЕНИЕ ТРАЕКТОРИИ НАД ЛИНИЕЙ ПРИЦЕЛИВАНИЯ».
Пристрелка АКМ на 300 метров.
Дальность: 100 м.
Прицел: 3
Мишень: белый фон 500х1000 мм с чёрным прямоугольником 350х250 мм.
Точка прицеливания: середина нижнего края чёрного прямоугольника.
Контрольная точка: на чёрном прямоугольнике по отвесной линии на расстоянии 25 см над точкой прицеливания.
Количество выстрелов до контроля: 4
Кучность: нормальная, если все 4-е попадания вмещаются в круг диаметром 15 см.
СТП: если кучность нормальная определяем среднюю точку попадания.
Для определения СТП по 4 пробоинам нужно:
- соединить прямой линией две ближайшие пробоины и расстояние между ними разделить пополам;
- полученную точку соединить с третьей пробоиной и расстояние между ними разделить на три равные части;
- точку деления, ближайшую к двум первым пробоинам, соединить с четвёртой пробоиной и расстояние между ними разделить на четыре равные части.
Точка деления, ближайшая к первым трем пробоинам, и будет средней точкой попадания (СТП – рис 47, а).
СТП можно определить если соединить пробоины попарно, затем соединить середины обеих прямых и полученную линию разделить пополам. Точка деления и будет средней точкой попадания (СТП – рис 47, б). Если все 4 пробоины не вмещаются в круг диаметром 15 см, среднюю точку попадания разрешается определять по трём более кучно расположенным пробоинам при условии, что «отрыв» – 4-я пробоина удалена от СТП трёх пробоин более чем на 2.5 радиуса круга, вмещающего эти пробоины (СТП – рис 47, г).
ВАЖНО: Пока не отстреляли все 4 выстрела, куда попали не смотреть и до определения СТП вообще ничего не трогать и не крутить.
ВНЕСЕНИЕ ПОПРАВОК
Если при стрельбе СТП отклонилась от контрольной в какую-либо сторону более чем на 5 см, то соответсвенно этому производится изменение положения мушки:
1) Если СТП ниже – мушку ввинтить.
2) Если СТП выше – мушку вывинтить.
3) Если СТП левее – полозок мушки сместить влево.
4) Если СТП правее – ползунок мушки сместить вправо.
При перемещении мушки в сторону на 1 мм, СТП при стрельбе на 100 метров смещается на 26 см. Один полный оборот мушки перемещает СТП по высоте при стрельбе на 100 метров на 20 см.
Баллистическая таблица для АКМ и патрона ЛПЗ “7.62×39 LCW FMJ 123 gr”
По материалам сайта travmatik.com
(1 голосов, средний: 5,00 из 5)
ЗАКОН РАССЕИВАНИЯ И ВЕЛИЧИНЫ, ХАРАКТЕРИЗУЮЩИЕ РАССЕИВАНИЕ
Пробоины на щите, полученные в результате серии выстрелов, располагаются в определенном порядке, подчиняясь действию закона, называемого законом рассеивания. Основные положения закона рассеивания таковы:
а) пробоины на щите располагаются на определенной площади, за пределами которой пробоин не будет; б) вокруг средней точки попадания пробоины располагаются гуще, чем по краям (рис. 62); в) если через среднюю точку попадания провести вертикальную линию, то по обеим сторонам от нее количество пробоин будет одинаковое; одинаковое же количество пробоин будет по обе стороны от горизонтальной линии, проведенной через среднюю точку попадания (рис.
62, а). Для измерения рассеивания пользуются сердцевинной полосой и сердцевиной. Сердцевинной полосой называют полосу, которая вмещает 70% всех пробоин и своей серединой совмещается с линией, проходящей через среднюю точку попадания (рис. 62, а, б). Вертикальная площадь рассеивания содержит по высоте и ширине по три сердцевинных полосы.

Рис.62. Закон рассеивания выстрелов
Прямоугольник, образованный пересечением вертикальной и горизонтальной сердцевинных полос в центре площади рассеивания, называется сердцевиной (рис. 62, в). Сердцевина вмещает 50% всех попавших снарядов. Другая половина снарядов распределяется по остальным восьми прямоугольникам, образованным пересечением сердцевинных полос, причем в крайних угловых прямоугольниках будет вмещаться по 2,5% всех попавших снарядов, а в крайних средних прямоугольниках — по 10% всех попавших снарядов (рис. 62, в).
Места падения снарядов на горизонтальный участок местности будут тоже подчиняться закону рассеивания, причем ширина площади рассеивания будет равна ширине площади рассеивания на вертикальном щите, длина же будет значительно больше. Рассеивание на горизонтальном участке местности точно так же измеряется сердцевинными полосами по ширине и по дальности и сердцевиной. Сердцевинные полосы и сердцевины для одного и того же оружия и снаряда на разных дальностях неравны, потому что траектории идут расходящимся пучком. Величина сердцевинных полос по ширине, высоте и дальности обычно дается в таблицах стрельбы.
РАСЧЕТ ВОЗМОЖНОГО ЧИСЛА ПОПАДАНИЙ
Зная закон рассеивания, величину рассеивания и положение средней точки попадания по отношению к цели, стрелок может заранее рассчитать число попаданий, которое можно в среднем ожидать при стрельбе по заданной цели.

Рис. 63. Подсчет возможного числа попаданий (заштрихованный прямоугольник — цель, незаштрихованный — площадь рассеивания; А — средняя точка попадания; Б — центр цели).
Рис. 64. Подсчет возможного числа попаданий (заштрихованный прямоугольник -цель; незаштрихованный — площадь рассеивания; А — средняя точка попадания).
Действительно, если средняя точка попадания находится на уровне центра цели, но правее ее на три сердцевинных полосы, то можно заранее сказать, что ни один снаряд в цель не попадет (рис. 63, а). Если же средняя точка попадания совпадает с центром цели и цель по величине равна сердцевине (рис. 63, б), то очевидно, что из всего числа выпущенных снарядов в цель попадет 50%, т. е. половина.
Для подсчета количества попаданий, которое в среднем можно ожидать при стрельбе по данной цели на заданной дальности стрельбы, поступают так.
Вычерчивают в произвольном масштабе площадь рассеивания (рис. 64). Далее, в том же масштабе, на площадь рассеивания наносят площадь цели, причем со средней точкой попадания совмещается точка цели, через которую проходит средняя траектория.
Затем, считая, что в каждом прямоугольнике площади рассеивания, образованном пересечением сердцевинных полос, пробоины располагаются равномерно, подсчитывают по отношению площади цели к площади рассеивания возможное число попаданий. Пример. Пусть площадь рассеивания по отношению к площади цели располагается так, как показано на рис. 80. Очевидно, что в часть площади а попадает 25% выпущенных снарядов, так как она наполовину меньше сердцевины; в части же площади б в в попадает по 2,5% выпущенных снарядов, так как эти части площади цели в четыре раза меньше соответствующих прямоугольников площади рассеивания, образованных пересечением сердцевинных полос. Таким образом, общий ожидаемый процент попадания будет равен:
ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ТОЧКИ ПОПАДАНИЯ
Для того чтобы найти установки прицела и целика, при которых средняя точка попадания будет совмещаться с центром мишени, стрелку нужно будет определять среднюю точку попадания.
При наличии двух пробоин средняя точка попадания определяется так. Обе пробоины соединяются прямой линией, которую затем делят пополам (рис. 65, а). Середина этой линии (точка А) и будет средней точкой попадания для двух пробоин.

Рис.65. Определение средней точки попадания
Среднюю точку попадания трех пробоин определяют таким образом (рис. 65, б). Соединяют две близлежащие пробоины прямой линией, которую затем делят пополам. От точки деления (точки К) проводят линию к третьей пробоине и делят эту линию на три равные части. Точка деления, находящаяся ближе к первой линии, и будет средней точкой попадания (точка А) для трех пробоин.
При большом количестве пробоин среднюю точку попадания находят следующим образом (рис. 65, в). Проводят на щите вертикальную линию так, чтобы справа и слева от нее было одинаковое количество пробоин. Затем проводят горизонтальную линию, причем выше и ниже ее тоже должно быть одинаковое количество пробоин. Точка пересечения вертикальной и горизонтальной линий и будет средней точкой попадания.
| Вперед > |
Источник: sk-atrium.su
Что называется средней точкой попадания
ЗАКОН РАССЕИВАНИЯ И ВЕЛИЧИНЫ, ХАРАКТЕРИЗУЮЩИЕ РАССЕИВАНИЕ
Пробоины на щите, полученные в результате серии выстрелов, располагаются в определенном порядке, подчиняясь действию закона, называемого законом рассеивания.
Основные положения закона рассеивания таковы:
а) пробоины на щите располагаются на определенной площади, за пределами которой пробоин не будет;
б) вокруг средней точки попадания пробоины располагаются гуще, чем по краям (рис. 62);
в) если через среднюю точку попадания провести вертикальную линию, то по обеим сторонам от нее количество пробоин будет одинаковое; одинаковое же количество пробоин будет по обе стороны от горизонтальной линии, проведенной через среднюю точку попадания (рис. 62, а).
Для измерения рассеивания пользуются сердцевинной полосой и сердцевиной.
Сердцевинной полосой называют полосу, которая вмещает 70% всех пробоин и своей серединой совмещается с линией, проходящей через среднюю точку попадания (рис. 62, а, б).
Вертикальная площадь рассеивания содержит по высоте и ширине по три сердцевинных полосы.
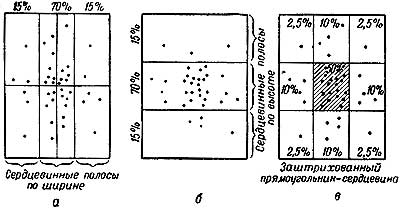
Рис.62. Закон рассеивания выстрелов
Прямоугольник, образованный пересечением вертикальной и горизонтальной сердцевинных полос в центре площади рассеивания, называется сердцевиной (рис. 62, в). Сердцевина вмещает 50% всех попавших снарядов. Другая половина снарядов распределяется по остальным восьми прямоугольникам, образованным пересечением сердцевинных полос, причем в крайних угловых прямоугольниках будет вмещаться по 2,5% всех попавших снарядов, а в крайних средних прямоугольниках — по 10% всех попавших снарядов (рис. 62, в).
Места падения снарядов на горизонтальный участок местности будут тоже подчиняться закону рассеивания, причем ширина площади рассеивания будет равна ширине площади рассеивания на вертикальном щите, длина же будет значительно больше.
Рассеивание на горизонтальном участке местности точно так же измеряется сердцевинными полосами по ширине и по дальности и сердцевиной.
Сердцевинные полосы и сердцевины для одного и того же оружия и снаряда на разных дальностях неравны, потому что траектории идут расходящимся пучком.
Величина сердцевинных полос по ширине, высоте и дальности обычно дается в таблицах стрельбы.
РАСЧЕТ ВОЗМОЖНОГО ЧИСЛА ПОПАДАНИЙ
Зная закон рассеивания, величину рассеивания и положение средней точки попадания по отношению к цели, стрелок может заранее рассчитать число попаданий, которое можно в среднем ожидать при стрельбе по заданной цели.
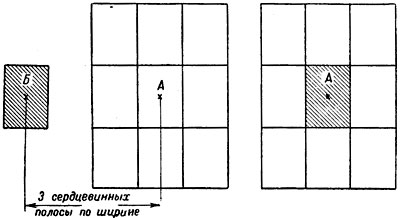
Рис. 63. Подсчет возможного числа попаданий
(заштрихованный прямоугольник — цель,
незаштрихованный — площадь рассеивания;
А — средняя точка попадания; Б — центр цели).
Действительно, если средняя точка попадания находится на уровне центра цели, но правее ее на три сердцевинных полосы, то можно заранее сказать, что ни один снаряд в цель не попадет (рис. 63, а). Если же средняя точка попадания совпадает с центром цели и цель по величине равна сердцевине (рис. 63, б), то очевидно, что из всего числа выпущенных снарядов в цель попадет 50%, т. е. половина.
Для подсчета количества попаданий, которое в среднем можно ожидать при стрельбе по данной цели на заданной дальности стрельбы, поступают так.
Вычерчивают в произвольном масштабе площадь рассеивания (рис. 64). Далее, в том же масштабе, на площадь рассеивания наносят площадь цели, причем со средней точкой попадания совмещается точка цели, через которую проходит средняя траектория.
Затем, считая, что в каждом прямоугольнике площади рассеивания, образованном пересечением сердцевинных полос, пробоины располагаются равномерно, подсчитывают по отношению площади цели к площади рассеивания возможное число попаданий.
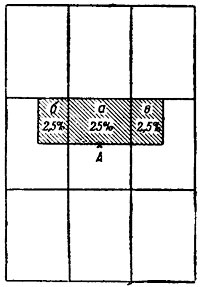
Пример. Пусть площадь рассеивания по отношению к площади цели располагается так, как показано на рис. 80. Очевидно, что в часть площади а попадает 25% выпущенных снарядов, так как она наполовину меньше сердцевины; в части же площади б в в попадает по 2,5% выпущенных снарядов, так как эти части площади цели в четыре раза меньше соответствующих прямоугольников площади рассеивания, образованных пересечением сердцевинных полос. Таким образом, общий ожидаемый процент попадания будет равен:
ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ТОЧКИ ПОПАДАНИЯ
Для того чтобы найти установки прицела и целика, при которых средняя точка попадания будет совмещаться с центром мишени, стрелку нужно будет определять среднюю точку попадания.
При наличии двух пробоин средняя точка попадания определяется так. Обе пробоины соединяются прямой линией, которую затем делят пополам (рис. 65, а). Середина этой линии (точка А) и будет средней точкой попадания для двух пробоин.
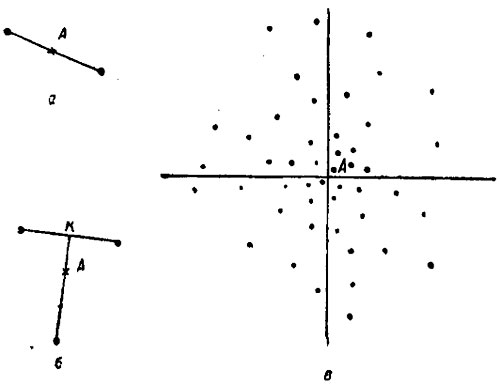
Рис.65. Определение средней точки попадания
Среднюю точку попадания трех пробоин определяют таким образом (рис. 65, б). Соединяют две близлежащие пробоины прямой линией, которую затем делят пополам. От точки деления (точки К) проводят линию к третьей пробоине и делят эту линию на три равные части. Точка деления, находящаяся ближе к первой линии, и будет средней точкой попадания (точка А) для трех пробоин.
При большом количестве пробоин среднюю точку попадания находят следующим образом (рис. 65, в). Проводят на щите вертикальную линию так, чтобы справа и слева от нее было одинаковое количество пробоин. Затем проводят горизонтальную линию, причем выше и ниже ее тоже должно быть одинаковое количество пробоин. Точка пересечения вертикальной и горизонтальной линий и будет средней точкой попадания.
Источник: pro-tank.ru