Как-то сидели мы с martreya , iiryna и deadvom в пиццерии и мне почему-то пришёл в голову вопрос, который я позже задавал в анкете:
Равны ли числа 0,(9) и 1?
Вопрос этот, наверное, несколько странный и многих, особенно нематематиков, может удивить и ответа на него не будет.
Мне здесь хочется немного прояснить свои и не только свои соображения по этому поводу. Начну издалека.
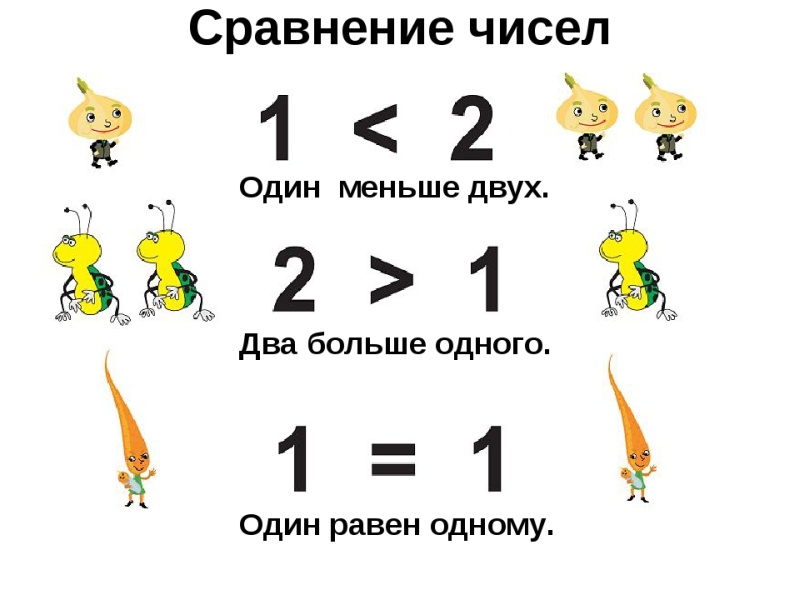
Как мы знаем, число — это одно из основополагающих понятий математики, мир чисел постоянно пополнялся на протяжении развития человечества. В первом классе мы изучали самые первые числа: 1, 2, 3. Эти числа называются натуральными, и их множество обозначается буквой N. В рамках этих чисел можно отлично выполнять операции сложения и умножения.
Если же мы захотим применять вычитание, то из подсознания выплывает фраза вроде «Из 2 яблок нельзя вычесть 4» или что-то в этом духе. Таким образом, мы получаем какие-то ограничения, которые расширяются введением отрицательных чисел. Множество всех отрицательных и положительных чисел называется множеством целых чисел и обозначается буквой Z. В рамках этих чисел отрицание уже выполняется без всяких проблем (2 — 4 = -2).
Взрываем мозги. Оказывается 0=1 | Ботай со мной #001 | Борис Трушин !
Следующей общеизвестной арифметической операцией является деление. Если поделить 1 на 2, то получится число не из множества целых чисел. Таким образом, снова придётся расширять известные числа, чтобы вместить результаты и этой операции.
Числа которые представимы в виде частного, то есть дроби m / n (m — числитель, n — знаменатель) — называются рациональными числами (множество Q). По своей сути, дроби — это как раз и есть рациональные числа, то есть обыкновенная дробь представляет собой частное, а результат деления числителя на знаменатель и есть рациональное число.
Опять же, вспомнинаем школу и на ум приходят задачи типа «сложить треть яблока с половиной яблока» и некоторые проблемы, возникающие при сложении дробей. Проблема состояла в том, что их надо было приводить к общему знаменателю (то есть 1/3 + 1/2 = 3/6 + 2/6 = 5/6), поскольку складывать без проблем можно было только дроби с одинаковым знаменателем. Соответственно, для того, чтобы от этих проблем избавиться, и из-за того, что у нас принята десятичная система счисления, были введены десятичные дроби. То есть такие дроби, у которых знаменатель — какая-то степень 10, то есть 3/10, 12/100, 13/1000 и т.д. Записывают их либо с запятой как у нас — (2,34) , либо с точкой, как принято на Западе (2.34).
Возникает вопрос: «а как перевести обычные дроби в десятичные?». Вспоминая деление уголком, можно набросать нечто такое:
Если говорить формально — то задача перевода из обычной дроби в десятичную представляет собой задачу нахождения такой наименьшей степени десятки, которая будет делиться на знаменатель заданной обычной дроби. То есть например для перевода дроби 3 / 8: берём знаменатель 8 и перебираем степени 10 до тех пор, пока какая-то степень 10 не станет делиться на 8: 10 не делится, 100 не делится, а вот 1000 делится (1000 / 8 = 125), значит 3 / 8 = 375 / 1000 = 0,375.
Правда ли, что 0,(9)=1? Бесконечные десятичные дроби | Ботай со мной #003 | Борис Трушин ||
Однако, что делать, если такой степени не находится или в случае деления уголком — процесс не заканчивается? Например, попробуем поделить 1 на 3:
Как мы видим — процесс через некоторое время зацикливается — то есть повторяются те же остатки, и мы точно знаем, что следующие цифры будут повторять предыдущие.
Таким образом имеем, что:
1/3 = 0.333333.
Терпение, мы уже близки к ответу на вопрос 🙂 Для того, чтобы отразить тот факт, что тройка в десятичной записи числа 1/3 повторяется и не писать троеточий — было введено специальное обозначение 0,(3). Часть в скобках называется «периодом» дроби, то есть бесконечно периодически повторяющейся частью дроби, а сама дробь — периодической. Таким образом, запись дроби с периодом является лишь иной формой записи обычного рационального числа, возникающей при переходе к конкретной системе счисления (в нашем случае десятичной) и период появляется, если в разложении на простые множители знаменателя уже сокращённой дроби присутствуют сомножители, на которые не делится основание системы счисления (например 6 = 2 * 3, 10 не делится на 3, потому у дроби 1/6 есть период в десятичной системе счисления). Кроме того, можно показать, что любая периодическая дробь является рациональным числом (то есть числом вида m / n), всего лишь представленным в альтернативном виде.
Таким образом можно смело записать что 0,(3) = 1/3, поскольку это одно и то же число, записанное различным образом. Соответственно, умножив на 3 каждую из частей уравнения, мы получаем, что 0,(9) = 1. Такое доказательство немного напоминает магию, однако всё дело в том, что по сути не существует чисел, разделив столбиком которые, мы могли бы получить число 0,(9) так, как мы получили 0,(3) разделив 1 и 3. Так что можно и усомниться в праве на существования у этого числа. Однако было бы нецелостно и математически нестрйоно отказываться от периодической формы записи в том случае, если число в периоде — 9, то есть 0,(9) или 1,(9) и т.д.
Поэтому число 0,(9) в данный момент вполне признано и является лишь альтернативной, неудобной и ненужной формой записи числа 1.
Как мы видим, определение периодических дробей не имеет никакого отношения к рядам, анализу бесконечно малых величин, пределам и тому подобным вещам, преподаваемым в высшей школе.
Резюмируя, можно сказать, что данная форма записи является всего лишь артефактом, вызванным применением конкретных систем счисления (в нашем случае десятичной системы). Насколько мне известно, некоторые математики (которых цитировал в одной из своих статей весьма известный Д. Кнут) ратуют за упразднение таких двузначных и спорных представлений чисел как 0,(9) и некоторых других.
Надеюсь, что объяснения были вполне понятными и интересными. Все возникшие вопросы, замечания и исправления — буду рад видеть в комментариях!
- Current Mood: mathy
Источник: dying-sphynx.livejournal.com
Вопрос по математике. Что больше 0.02 или 0.05, почему?
Простите за такой, наверное простой вопрос по математике.
комментировать
в избранное up —>
11 ответов:
ворчу нов [106K]
5 лет назад
Потому что. Смотрим на рисунок.
0,02 это два кусочка от 0,1
0,05 это пять кусочков от 0,1
Пять больше двух?
Если сомневаетесь, возьмите два яблока (кирпича и т.д.) и пять яблок (кирпичей и т.д.).
После этого вопросов больше думаю не будет.

автор вопроса выбрал этот ответ лучшим
комментировать
в избранное ссылка отблагодарить
Azama tik [55.1K]
6 лет назад
Доброго времени суток.
Так как в обоих представленных числах после запятой стоит одинаковое количество цифр (по два), то можно их сравнивать таким образом: перемещаем запятую на две цифры и получаем 5 и 2 > а число 5 больше чем 2. Значит, число 0,05 больше числа 0,02.
Можно также представить числа в виде дробей: 5/100 и 2/100. Одинаковые заменители, поэтому сравниваем числители (5>2).
Ответ: 0,05 больше 0,02.
комментировать
в избранное ссылка отблагодарить
barvi nok79 [62.2K]
6 лет назад
давайте умножим на 100 оба этих числа : от этого их соотношение не изменится.
Очевидно, что 2 меньше чем 5.
Отсюда прямиком и следует, что 0,02 меньше чем 0,05.
Этот способ годится и во всех других случаях.
комментировать
в избранное ссылка отблагодарить
Smile dimas ik [32K]
5 лет назад
Очень часто люди могут делать ошибки даже в легких заданиях, так как некоторые дробовые числа могут звучать будто больше, но гораздо меньше по наличию, в нашем случае 0,05 больше чем 0,02 и потому при вычислениях стоит это помнить.
комментировать
в избранное ссылка отблагодарить
Galin a7v7 [118K]
7 лет назад
Вот как я объясняю своим малышам такие задачи.Когда десятичная дробь с ноликами.посчитайте сколько нулей после запятой.Если одинаковое число.то сравните цифры.и та больше дробь.у которой цифра больше.Это вот про этот пример тоже объяснение- 0.05>0.02.А еще объяснение-тоже для деток.Торт разрезали на 100 кусков.1 кусок =1100.а 5100 и 2100 это тоже самое в сравнении как 2 куска и 5 кусков торта.Ичто больше 2 куска или 5 кусков?
Источник: www.bolshoyvopros.ru
Сравнение отрицательных чисел: правило, примеры
В статье ниже озвучим принцип сравнения отрицательных чисел: сформулируем правило и применим его в решении практических задач.
Правило сравнения отрицательных чисел
В основе правила – сравнение модулей исходных данных. По сути, сравнить два отрицательных числа – значит сравнить положительные числа, равные модулям сравниваемых отрицательных чисел.
При сравнении двух отрицательных чисел меньшим является то число, модуль которого больше; бОльшим является то число, модуль которого меньше. Заданные отрицательные числа являются равными, если их модули равны.
Сформулированное правило применимо как к отрицательным целым числам, так и к рациональным и действительным.
Геометрическое толкование подтверждает принцип, озвученный в указанном правиле: на координатной прямой отрицательное число, которое является меньшим, находится левее, чем большее отрицательное. Это утверждение, в общем, верно для любых чисел.
Примеры сравнения отрицательных чисел
Самым простым примером сравнения отрицательных чисел является сравнение целых чисел. С подобной задачи и начнем.
Необходимо сравнить отрицательные числа — 65 и — 23 .
Решение
Согласно правилу, для осуществления действия сравнения отрицательных чисел сначала необходимо определить их модули. | — 65 | = 65 и | — 23 | = 23 . Теперь сравним положительные числа, равные модулям заданных: 65 > 23 . Применим вновь правило, гласящее, что больше то отрицательное число, модуль которого меньше. Таким образом, получим: — 65 < — 23 .
Ответ: — 65 < — 23 .
Чуть сложнее сравнивать отрицательные рациональные числа: действие в конечном счете приводит к сравнению обыкновенных или десятичных дробей.
Необходимо определить, какое из заданных чисел больше: — 4 3 14 или — 4 , 7 .
Решение
Определим модули сравниваемых чисел. — 4 3 14 = 4 3 14 и | — 4 , 7 | = 4 , 7 . Теперь сравним полученные модули. Целые части дробей равны, так что приступим к сравнению дробных частей: 3 14 и 0 , 7 . Осуществим перевод десятичной дроби 0 , 7 в обыкновенную: 7 10 , найдем общие знаменатели сравниваемых дробей, получим: 15 70 и 49 70 . Тогда результатом сравнения станет: 15 70 < 49 70 или 3 14 4 3 14 . fff Применив правило сравнения отрицательных чисел, имеем: — 4 3 14 < — 4 , 7
Также можно было осуществить сравнение путем перевода обыкновенной дроби в десятичную. Разница – лишь в удобстве вычисления.
Ответ: — 4 3 14 < — 4 , 7
Сравнение отрицательных действительных чисел производится согласно тому же правилу.
Источник: zaochnik.com
Сравнение в математике — как определить, какие из чисел больше или меньше
Сравнение чисел — одна из самых легких и приятных тем из курса математики. Впрочем, нужно сказать, что она не так уж и проста. Например, мало кто испытывает трудности со сравнением однозначных или двузначных положительных чисел.
Но числа с большим количеством знаков уже вызывают проблемы, часто люди теряются при сравнении отрицательных чисел и не помнят, как сравнить два числа с разными знаками. На все эти вопросы мы и постараемся ответить.
Правила относительно сравнения положительных чисел
Начнем с самого простого — с чисел, перед которыми не стоит никакого знака, то есть с положительных.
- Прежде всего, стоит запомнить, что все положительные числа по определению больше нуля, даже если речь идет о дробном числе без целого. Например, десятичная дробь 0,2 будет больше, чем нуль, поскольку на координатной прямой соответствующая ей точка все-таки отстоит от нуля на два небольших деления.
- Если речь идет о сравнении двух положительных чисел с большим количеством знаков, то нужно сравнивать каждый из разрядов. Например — 32 и 33. Разряд десятков у этих чисел одинаков, но число 33 больше, поскольку в разряде единиц «3» больше, чем «2».
- Как сравнить между собой две десятичные дроби? Здесь нужно смотреть прежде всего на целую часть — например, дробь 3,5 будет меньше, чем 4,6. А если целая часть одинакова, но различаются знаки после запятой? В этом случае действует правило для целых чисел — нужно сравнивать знаки по разрядам до тех пор, пока не обнаружатся большие и меньшие десятые, сотые, тысячные доли. Например — 4,86 больше 4,75, поскольку восемь десятых больше, чем семь.
Сравнение отрицательных чисел
Если у нас в задаче есть некие числа –а и –с, и нам нужно определить, какое из них больше, то применяется универсальное правило. Сначала выписываются модули этих чисел — |a| и |с| — и сравниваются между собой. То число, модуль которого больше, окажется меньшим в сравнении отрицательных чисел, и наоборот — большим числом будет то, модуль которого меньше.
Что делать, если сравнить нужно отрицательное и положительное число?
Здесь работает всего одно правило, и оно элементарно. Положительные числа всегда больше чисел со знаком «минус» — какими бы они ни были. Например, число «1» всегда будет больше числа «-1458» просто потому, что единица стоит справа от нуля на координатной прямой.
Также нужно помнить, что любое отрицательное число всегда меньше нуля.
Источник: infoogle.ru