«Теплоход после стоянки возвращается в пункт оправления» — ещё один вид задач по алгебре, которые в ОГЭ по математике включены под номером 21, а в ЕГЭ — №11.
Такие задачи можно решить, составив уравнение. За x обычно принимают либо собственную скорость теплохода (баржи), либо скорость течения (что неизвестно, то и берём за x). Если скорость известна, за x можно принять время или расстояние.
Теплоход проходит по течению реки 210 км и после стоянки возвращается в пункт оправления. Найдите скорость теплохода в неподвижной воде , если скорость течения реки равна 4 км/ч, стоянка длится 9 часов, а в пункт отправления теплоход возвращается через 27 часов после отплытия из него.
Пусть скорость теплохода в неподвижной воде равна x км/ч.
Так как стоянка длится 9 часов, а в пункт отправления теплоход возвращается через 27 часов после отплытия из него, то на весь путь теплоход затратил 27-9=18 часов.
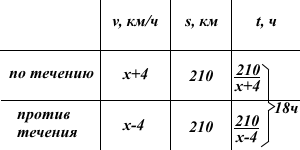
Егэ математика В12. Скорость лодки
Составим уравнение и решим его:
![[ frac{{210}}{{x + 4}} + frac{{210}}{{x - 4}} = 18__left| {:6} right. ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-07fa0f8d278ec917403b5740dde73364_l3.png)
![[ frac{{35^{backslash (x - 4)} }}{{x + 4}} + frac{{35^{backslash (x + 4)} }}{{x - 4}} = 3^{backslash (x^2 - 16)} ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-31c05825ea985d647b8e7afc22ee78c1_l3.png)
![[ frac{{35(x - 4) + 35(x + 4) - 3(x^2 - 16)}}{{(x - 4)(x + 4)}} = 0 ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-30cb87488c94cdf055dcc515f461b935_l3.png)
![[ frac{{35x - 140 + 35x + 140 - 3x^2 + 48}}{{(x - 4)(x + 4)}} = 0 ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-741d9b8596e63b19138379518df661f6_l3.png)
![[ frac{{ - 3x^2 + 70x + 48}}{{(x - 4)(x + 4)}} = 0__left| {:( - 1)} right. ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-3190f38a11472411323cccfefb2d3c7b_l3.png)
![[ Leftrightarrow left{ begin{array}{l} 3x^2 - 70x - 48 = 0; \ x ne 4;x ne - 4 \ end{array} right. ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-346c3d5fc534bc12da2b5b84d5a527ff_l3.png)
![[D = b^2 - 4ac = 70^2 - 4 cdot 3 cdot 48 = 5476, ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-272106c1b7700217c80bfd1cf29c9117_l3.png)
![[ x_{1,2} = frac{{ - b pm sqrt D }}{{2a}} = frac{{70 pm 74}}{6} ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-5528cd7396fe6cfba2a1bb0b07312f19_l3.png)
Задача.2 часть ОГЭ по математике
x1=24 или x2=-2/3 — не удовлетворяет условию задачи.
Скорость теплохода в неподвижной воде равна 24 км/ч.
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, баржа отправилась назад и вернулась в пункт А в 18:00. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 6 км/ч.
Пусть скорость течения реки равна x км/ч.
Так как баржа вышла из пункта А в 10:00, вернулась назад в 18:00, пробыла в пункте В 1 час 20 минут, то на весь путь она затратила 18 часов-10 часов -1 час 20 минут=6 часов 40 минут. Выразим время в часах:
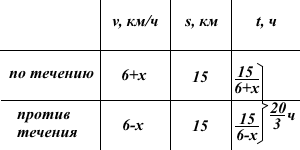
Составим и решим уравнение:
![[ frac{{15}}{{6 + x}} + frac{{15}}{{6 - x}} = frac{{20}}{3}__left| {:5} right. ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-1205fb890d601df693c6eba59b52941d_l3.png)
![[ frac{{3^{backslash 3(6 - x)} }}{{6 + x}} + frac{{3^{backslash 3(6 + x)} }}{{6 - x}} = frac{4}{3}^{backslash (36 - x^2 )} ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-bed591cc76c6daf0370dc720b575ae1e_l3.png)
![[ frac{{9(6 - x) + 9(6 + x) - 4(36 - x^2 )}}{{3(6 + x)(6 - x)}} = 0 ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-a53b2932f429789316518301e61dd418_l3.png)
![[ frac{{54 - 9x + 54 + 9x - 144 + 4x^2 }}{{3(6 + x)(6 - x)}} = 0 ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-9f20f4120d40eb36f5ca580bc19e5c72_l3.png)
![[ frac{{4x^2 - 36}}{{3(6 + x)(6 - x)}} = 0__left| {:4 Leftrightarrow } right. ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-5412f71ad6a6bbce3139a3cb653e480c_l3.png)
![[ Leftrightarrow left{ begin{array}{l} x^2 - 9 = 0; \ x ne - 6;x ne 6 \ end{array} right.]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-6ab45f150eaeb2e5e8cfe1a3230678d3_l3.png)
x1=3 или x2=-3 — не удовлетворяет условию задачи.
Теплоход, скорость которого в неподвижной воде равна 27 км/ч, проходит некоторое расстояние по реке и после стоянки возвращается в исходный пункт. Скорость течения равна 1 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 32 часа после отправления из него. Сколько километров проходит теплоход за весь рейс?
Так как в исходный путь теплоход возвращается через 32 часа после отправления из него, а стоянка длится 5 часов, то общее время в пути равно 32-5=27 часов.
Скорость теплохода в неподвижной воде равна 27 км/ч, скорость течения реки равна 1 км/ч. Значит, по течению теплоход движется со скоростью 27+1=28 км/ч, против течения — 27-1=26 км/ч.
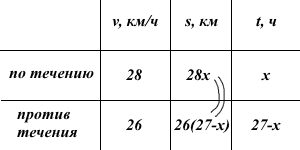
Пусть x часов — время движения теплохода по течению, тогда (27-x)ч — время движения против течения.
По течению и против течения теплоход прошёл одинаковое расстояние. Составим уравнение и решим его:
13 часов — время движения теплохода по течению. За это время он прошёл 28·13=364 км.
Значит, за весь рейс теплоход прошёл 364+364=728 км.
Источник: www.algebraclass.ru
Задание 11. ЕГЭ. Теплоход, скорость которого в неподвижной воде равна 16 км/ч.
Задание. Теплоход, скорость которого в неподвижной воде равна 16 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 2 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 53 часа после отплытия из него. Сколько километров прошёл теплоход за весь рейс?
Решение:
Пусть x км теплоход проходит по течению реки до стоянки.
Так как скорость теплохода по течению реки равна 16 + 2 = 18 км/ч,
то для прохождения x км теплоход затратил
Так как скорость теплохода против течения реки равна 16 – 2 = 14 км/ч, то на обратный путь теплоход затратил
Учитывая, что стоянка теплохода составила 5 часов, а в исходный пункт теплоход возвратился через 53 часа после отплытия из него, составим уравнение
Получили, что 378 км теплоход проходит по течению реки до стоянки, тогда за весь рейс теплоход прошёл 378·2 = 756 км.
Ответ: 756
Источник: bezikev.ru
ОГЭ, Математика.
Геометрия: Задача №D253EC
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
Решение задачи:
Рассмотрим треугольник АОВ. АО=ОВ, т.к. это радиусы окружности. Следовательно, треугольник АОВ — равнобедренный. Следовательно, ОВА = ОАВ = 60° (по свойству равнобедренного треугольника). Заметим, что АОВ тоже равен 60° (по теореме о сумме углов треугольника). 180°-60°-60°=60°.
Следовательно треугольник АОВ — равносторонний (по свойству равностороннего треугольника). Следовательно, ОВ=ОА=АВ=7.
Ответ: АВ=7.
Присоединяйтесь к нам.
Вы можете поблагодарить автора, написать свои претензии или предложения на странице ‘Про нас’
Другие задачи из этого раздела
Задача №FC110F
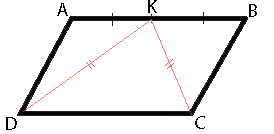
В параллелограмме ABCD точка K — середина стороны AB. Известно, что KC = KD. Докажите, что данный параллелограмм — прямоугольник.
Задача №383C46
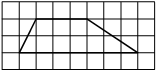
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Задача №0208A9
В треугольнике ABC угол C равен 90°, BC=2, sinA=0,2. Найдите AB.
Задача №273E7A
ABCDEFGHIJ — правильный десятиугольник. Найдите угол CAH. Ответ дайте в градусах.
Задача №201D88
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 154°. Найдите угол C. Ответ дайте в градусах.
Источник: otvet-gotov.ru