Шар подвешен на невесомой нерастяжимой нити длиной l = 0,5 м. Какую минимальную горизонтально направленную скорость vo надо сообщить шару, чтобы он сделал полный оборот в вертикальной плоскости?
Эта задача была размещена посетителями в разделе Решаем вместе 25 мая 2007 года.
где l — длина подвеса или нерастяжимой нити.
В верхней точке на шарик будут действовать 2 силы: сила тяжести mg (направлена вниз) и сила натяжения нити T (также направлена вниз). Эти силы сообщают шарику центростремительное ускорение, направленное вниз — к точке подвеса:
vo 2 = g4l + gl = 5gl.
Выполнив вычисления, получим: vo = √(5×10×0,5) = 5 (м/с).
Ответ: если шарик подвешен на нерастяжимой нити, его скорость должна составлять не менее 5 м/с.
Произведя вычисления, получим: vo = 2×√(10×0,5) = 4,47 (м/с).
- задачи с решениями
- законы сохранения
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Комментарии
Опубликовано 7 марта, 2010 — 14:07 пользователем KONDR
Физика # 05. Закон сохранения импульса
Объясните непонятливому. Почему, если подвешен на жестком стержне, то обязательно V = 0 в верхней точке?
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 7 марта, 2010 — 18:58 пользователем afportal
Если подвешен на нити, то скорость должна быть достаточной, чтобы шар в верхней точке не упал вниз (т.е. чтобы центробежная сила была больше силы тяжести). Если же шар подвешен на жестком стержне, то согнуться он не может, поэтому центробежная сила может быть нулевой, что происходит при нулевой скорости шара.
(Для наглядности можно посоветовать повращать в вертикальной плоскости швабру [поперечина на жестком стержне] и такую же деревяшку-поперечину на обычной веревке).
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 29 июня, 2012 — 15:03 пользователем kop_and
в самой первой формуле откуда взялось: mg • 2l ?
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 29 июня, 2012 — 15:06 пользователем afportal
Расстояние между нижней и верхней точками окружности — это диаметр. Другие словами, два радиуса (две длины нити).
mgh — потенциальная энергия.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 16 сентября, 2012 — 20:34 пользователем Scotland
1. Откуда взялось 10 в выражении vo = ?(5 × 10 × 0,5), т. е. почему g = 10? g — это ускорение или что-то другое?
2. Что за скорость v и чему она равна?
3. Что такое mv 2 и mvo?
4. Что такое gl и mgl ?
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 16 сентября, 2012 — 21:34 пользователем kop_and
1. 10 — это ускорение свободного падения.
2. v — это скорость в верхнем положении. Имеется в виду, когда шарик пройдёт половину половину окружности, у него будет скорость v. Скорость v = √(gl). Нашли мы её так: maц = mg + T, откуда a (ускорение) = v 2 / l (центростремительное ускорение).
Импульс, закон сохранения импульса в ОГЭ по физике
3 и 4. Сообщив шарику скорость vo, возникает кинетическая энергия, которая равна mvo 2 /2. Так как система замкнутая, кинетическая энергия превращается в потенциальную — mg × 2l и кинетическую — mv 2 /2.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Источник: www.afportal.ru
Из неподвижной лодки масса которой 60 кг, прыгает мальчик массой 30 кг со скоростью 4 м/с. какую массу преобретает лодка?
Мощность электродвигателя, приводящего в движение нефтемешалку, равна 1900 Вт. Определите сопротивление обмоток электродвигателя, если через них протекает за 2 часа заряд, равный 14400 Кл
Дано: P=1900Вт, q=14400Кл, t=2ч. R=?
Си: t=7200сек.
Формула: R=U/I; P=UI; I=q/t; U=Pt/q
Решение: U=Pt/q; U=1900Вт*7200сек/14400Кл=950В; R=950В/(14400Кл/7200сек)=475Ом.
4,4(2 оценок)
Самым частым проявлением метеочувствительности является головная боль. И атмосферное давление играет важную роль в развитии этого симптома.
ВЛИЯНИЕ АТМОСФЕРНОГО ДАВЛЕНИЯ НА САМОЧУВСТВИЕ
Комфортным для человека считается нормальное атмосферное давление 760 мм рт.ст. (1013,25 гПа) на уровне моря. Этот показатель уменьшается с увеличением высоты и возрастает при снижении температуры воздуха.
Как известно, атмосферное давление постоянно меняется. Его циклические изменения связаны с суточными, годовыми, сезонными и другими циклами в естественных метеорологических процессах. Нециклические изменения наблюдаются при формировании и разрушении циклонов и антициклонов.
Сильными скачками атмосферного давления принято считать межсуточные перепады от 10 гПа, резкими — 8-10 гПа, умеренными — 4-8 гПа, а слабыми — до 4 гПа. Незначительные перепады давления обычно никак не отражаются на самочувствии людей. Они уравновешиваются внутренним давлением организма. Но чем резче переход, тем организм человека к нему чувствительнее.
Поэтому атмосферное давление является одним из самых важных погодных факторов, влияющих на здоровье и самочувствие людей. Его колебания могут ощущать на себе даже те, кто считает себя здоровым и не относит к группе метеозависимых. Головная боль и атмосферное давление – симптом и фактор, сочетание которых встречается довольно часто.
Сниженное атмосферное давление (циклон) обычно сопровождается повышенной влажностью, осадками, облачностью, незначительным повышением температуры воздуха. Во время циклона воздух беден кислородом. Это отражается на работе системы кровообращения. При резком понижении давления скапливается избыточное количество растворенных газов в крови, тканях и различных органах.
Основные проявления негативного влияния циклона на человека – общая слабость, затруднение дыхания, одышка, мигрень, ухудшение работы желудочно-кишечного тракта. Наиболее подвержены влиянию циклона люди с низким артериальным давлением, нарушениями функции дыхания, сердечно-сосудистыми заболеваниями.
Источник: mozgotvet.com
Закон сохранения импульса, кинетическая и потенциальные энергии, мощность силы
Следует помнить, что речь идет о теле, которое можно представить как материальную точку. Импульс тела ($р$) называют также количеством движения. Понятие количества движения было введено в физику Рене Декартом (1596—1650). Термин «импульс» появился позже (impulsus в переводе с латинского означает «толчок»). Импульс является векторной величиной (как и скорость) и выражается формулой:
Направление вектора импульса всегда совпадает с направлением скорости.
За единицу импульса в СИ принимают импульс тела массой $1$ кг, движущегося со скоростью $1$ м/с, следовательно, единицей импульса является $1$ кг $·$ м/с.
Если на тело (материальную точку) действует постоянная сила в течение промежутка времени $∆t$, то постоянным будет и ускорение:
где, $↖$ и $↖$ — начальная и конечная скорости тела. Подставив это значение в выражение второго закона Ньютона, получим:
Раскрыв скобки и воспользовавшись выражением для импульса тела, имеем:
Здесь $↖-↖=∆p↖$ — изменение импульса за время $∆t$. Тогда предыдущее уравнение примет вид:
Выражение $∆p↖=F↖∆t$ представляет собой математическую запись второго закона Ньютона.
Произведение силы на время ее действия называют импульсом силы. Поэтому изменение импульса точки равно изменению импульса силы, действующей на нее.
Выражение $∆p↖=F↖∆t$ называется уравнением движения тела. Следует заметить, что одно и то же действие — изменение импульса точки — может быть получено малой силой за большой промежуток времени и большой силой за малый промежуток времени.
Импульс системы тел. Закон изменения импульса
Импульсом (количеством движения) механической системы называется вектор, равный сумме импульсов всех материальных точек этой системы:
Законы изменения и сохранения импульса являются следствием второго и третьего законов Ньютона.
Рассмотрим систему, состоящую из двух тел. Силы ($F_$ и $F_$ на рисунке, с которыми тела системы взаимодействуют между собой, называются внутренними.
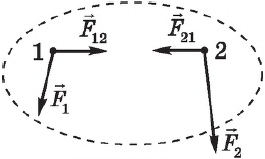
Пусть кроме внутренних сил на систему действуют внешние силы $↖$ и $↖$. Для каждого тела можно записать уравнение $∆p↖=F↖∆t$. Сложив левые и правые части этих уравнений, получим:
В левой части стоит геометрическая сумма изменений импульсов всех тел системы, равная изменению импульса самой системы — $>↖$.С учетом этого равенство $↖+↖=(↖+↖)∆t$ можно записать:
где $F↖$ — сумма всех внешних сил, действующих на тело. Полученный результат означает, что импульс системы могут изменить только внешние силы, причем изменение импульса системы направлено так же, как суммарная внешняя сила. В этом суть закона изменения импульса механической системы.
Внутренние силы изменить суммарный импульс системы не могут. Они лишь меняют импульсы отдельных тел системы.
Закон сохранения импульса
Из уравнения $>↖=F↖∆t$ вытекает закон сохранения импульса. Если на систему не действуют никакие внешние силы, то правая часть уравнения $>↖=F↖∆t$ обращается в ноль, что означает неизменность суммарного импульса системы:
Система, на которую не действуют никакие внешние силы или равнодействующая внешних сил равна нулю, называется замкнутой.
Закон сохранения импульса гласит:
Суммарный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел системы между собой.
Полученный результат справедлив для системы, содержащей произвольное число тел. Если сумма внешних сил не равна нулю, но сумма их проекций на какое-то направление равна нулю, то проекция импульса системы на это направление не меняется. Так, например, система тел на поверхности Земли не может считаться замкнутой из-за силы тяжести, действующей на все тела, однако сумма проекций импульсов на горизонтальное направление может оставаться неизменной (при отсутствии трения), т. к. в этом направлении сила тяжести не действует.
Реактивное движение
Рассмотрим примеры, подтверждающие справедливость закона сохранения импульса.
Возьмем детский резиновый шарик, надуем его и отпустим. Мы увидим, что когда воздух начнет выходить из него в одну сторону, сам шарик полетит в другую. Движение шарика является примером реактивного движения. Объясняется оно законом сохранения импульса: суммарный импульс системы «шарик плюс воздух в нем» до истечения воздуха равен нулю; он должен остаться равным нулю и во время движения; поэтому шарик движется в сторону, противоположную направлению истечения струи, и с такой скоростью, что его импульс по модулю равен импульсу воздушной струи.
Реактивным движением называют движение тела, возникающее при отделении от него с какой- либо скоростью некоторой его части. Вследствие закона сохранения импульса направление движения тела при этом противоположно направлению движения отделившейся части.
На принципе реактивного движения основаны полеты ракет. Современная космическая ракета представляет собой очень сложный летательный аппарат. Масса ракеты складывается из массы рабочего тела (т. е. раскаленных газов, образующихся в результате сгорания топлива и выбрасываемых в виде реактивной струи) и конечной, или, как говорят, «сухой» массы ракеты, остающейся после выброса из ракеты рабочего тела.
Когда реактивная газовая струя с большой скоростью выбрасывается из ракеты, сама ракета устремляется в противоположную сторону. Согласно закону сохранения импульса, импульс $m_
υ_p$, приобретаемый ракетой, должен быть равен импульсу $m_·υ_$ выброшенных газов:
Отсюда следует, что скорость ракеты
Из этой формулы видно, что скорость ракеты тем больше, чем больше скорость выбрасываемых газов и отношение массы рабочего тела (т. е. массы топлива) к конечной («сухой») массе ракеты.
Формула $υ_p=(>/)·υ_$ является приближенной. В ней не учитывается, что по мере сгорания топлива масса летящей ракеты становится все меньше и меньше. Точная формула для скорости ракеты была получена в 1897 г. К. Э. Циолковским и носит его имя.
Формула Циолковского позволяет рассчитать запасы топлива, необходимые для сообщения ракете заданной скорости.
Работа силы
Термин «работа» был введен в физику в 1826 г. французским ученым Ж. Понселе. Если в обыденной жизни работой называют лишь труд человека, то в физике и, в частности, в механике принято считать, что работу совершает сила. Физическую величину работы обычно обозначают буквой $А$.
Работа силы — это мера действия силы, зависящая от ее модуля и направления, а также от перемещения точки приложения силы. Для постоянной силы и прямолинейного перемещения работа определяется равенством:
где $F$ — сила, действующая на тело, $∆r↖$ — перемещение, $α$ — угол между силой и перемещением.
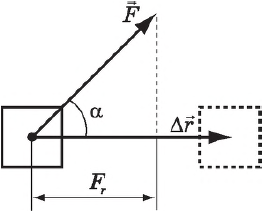
Работа силы равна произведению модулей силы и перемещения и косинуса угла между ними, т. е. скалярному произведению векторов $F↖$ и $∆r↖$.
Работа — величина скалярная. Если $α 0$, а если $90°
- ООО «Экзамер», 2015—2023
- Написать нам
- Юридические документы
Источник: examer.ru