Подсчитайте количество цифр после запятой. Количество цифр после запятой равно 1. Таким образом, умножьте и разделите 1.2 на 10, возведенное в степень 1, то есть 10, 1.2 x 10/10 = 12/10 = 6/5.
Аналогично, какая дробь равна 35 дюйма? Эквиваленты таблицы дюймов/мм
Похожие страницы:Блог
Какие есть 3 вида налогов?
Как найти среднюю точку между двумя точками?
Как вы делаете кадровые прогнозы?
Как найти начальную скорость, зная только время?
| 32 | 1/2 | 0.5 |
| 33 | 33/64 | 0.515625 |
| 34 | 17/32 | 0.53125 |
| 35 | 35/64 | 0.546875 |
• 28 марта 2003 г.
Как перевести 0.75 в дробь? Значение 0.75 как дробь равно 3/4.
Чему равно 2.8 в виде дроби? 2.8 в виде дроби 2 4/5.
Во-вторых, как превратить 22.22 в дробь? 22.22% в виде дроби 22.22/100. Если вы хотите, вы можете упростить его до 1111/5000. 3.
Десятичная дробь. Чтение и запись. 5 класс.
Сколько дробей в дюйме?
тогда какая дробь равна 1.3 дюйма? Ответ: 1.3 как дробь 13/10.
Что такое 39 дюйма как дробь? Дробные и десятичные эквиваленты.
| 36/64 | 18/32 | 0.5625 |
| 37/64 | 0.5781 | |
| 38/64 | 19/32 | 0.5938 |
| 39 / 64 | 0.6094 |
Как записать 33 как дробь?
Упрощенный 1/3 на самом деле эквивалентно 33 и 1/3 процента.
Как записать 0.875 в виде дроби? Как и в нашей предыдущей задаче, оказывается, что мы можем сократить эту дробь до наименьших членов, разделив ее числитель и знаменатель на 125. Делая это, мы находим, что 0.875 = 875/1000 эквивалентно 7/8.
Как перевести 1.75 в дробь?
Ответ: 1.75 в виде дроби выражается как 7/4.
Как превратить 7.03 в дробь? Шаги для преобразования десятичной дроби в дробь
- Запишите 7.03 как 7.031.
- 7.03 × 1001 × 100 = 703100.
- 703100
Как превратить 2.5 в дробь?
Ответ: Дробная форма 2.5 есть 5/2.
Чтобы преобразовать 2.5 в дробь, сначала мы запишем число в форме x/y, где x и y — положительные целые числа. Таким образом, 2.5 можно записать как 2.5/1. Для удаления десятичной дроби умножаем и делим на 10. И получаем, 2.5/1 х 10/10 = 25/10 = 5/2.
Как перевести 66.67 в дробь?
66.67% в виде дроби 66.67/100. Если вы хотите, вы можете упростить его до 6667/10000.
Как записать 66.67 как дробь? Выразите 66.67 в виде дроби
- Запишите 66.67 как 66.671.
- 66.67 × 1001 × 100 = 6667100.
- 6667100
Как перевести 55.55 в дробь? Шаги для преобразования десятичной дроби в дробь
- Запишите 55.55 как 55.551.
- 55.55 × 1001 × 100 = 5555100.
- 111120
Как прочитать тысячные доли дюйма?
Что такое 8 дюйма как дробь? Таблица преобразования дюймовых дробей – эквиваленты десятичных и метрических дробей
КАК НАУЧИТЬСЯ СЧИТАТЬ ДРОБИ / ВСЕГО 3 ПРАВИЛА
| 1/8 « | 0.125 « | 3.175 мм |
| 9 / 64 « | 0.140625 « | 3.571875 мм |
| 5 / 32 « | 0.15625 « | 3.96875 мм |
| 11 / 64 « | 0.171875 « | 4.365625 мм |
Как перевести футы и дюймы в дроби?
Методология заключается в умножьте количество футов на 12, прибавьте количество дюймов, разделите числитель на знаменатель, затем прибавьте десятичный результат к количеству дюймов.
Как записать 3.3 в виде дроби? 3.3 как дробь 3 3/10.
Какая дробь составляет 1.8 дюйма?
Таблица преобразования десятичных дробей в дробные
| 1.6 | 8/5 |
| 1.7 | 17/10 |
| 1.75 | 7/4 |
| 1.8 | 9/5 |
Как перевести дроби в дюймы? Методология заключается в том, чтобы умножьте количество футов на 12, прибавьте количество дюймов, разделите числитель на знаменатель, затем прибавьте десятичный результат к количеству дюймов.
Источник: reviews.tn
1/2 перевести в десятичную дробь
Довольно часто требуется в математике перевести обыкновенную дробь в десятичную. Связано это в первую очередь с тем, что десятичные дроби являются неким общепринятым стандартом и используются чаще обычных дробей. Например, в бланки государственных экзаменов разрешается записывать только десятичные дроби. Или не скажем же мы в магазине: «Дайте мне три вторых килограмма сахара».
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести простую дробь в десятичную, нужно разделить числитель на знаменатель (число над дробной чертой на число под ней). Рассмотрим несколько возможных случаев.
- Случай 1. У нас есть простая простая правильная дробь (<1) Возьмем заданную дробь ( 1 /2) и переведем ее в десятичную. Для удобства можно выполнить деление столбиком (или калькулятором). Делим 1 на 2 и получаем 0,5.
- Случай 2. У нас неправильная дробь (>1) или есть целая часть. Целую часть мы не трогаем, а если ее можно выделить, то выделяем. Например, 3 /2 = 1 1 /2 . Единицу мы оставляем, а с дробной частью производим уже известные нам действия. Ответ — 1,5.
- Случай 3. При делении у нас не получается конечное число, то есть ответ — бесконечная десятичная дробь. Есть два варианта. 1) Если дробь получилась периодическая (0,6666. ), то ответ можно записать так: 0,(6) . 2) Если дробь не периодическая, то мы можем округлить число до какой-либо цифры (до десятых, сотых), если только нам позволяет это сделать условие. Если нет, то лучше оставить число в виде простой дроби.
Для того чтобы преобразовать обыкновенную дробь в десятичную, нужно знаменатель обыкновенной дроби привести к 10, 100, 1000 и т.д. В качестве примера, преобразуем дробь 1/2:
1. Первым шагом необходимо найти целое число, которое преобразует знаменатель к 10, 100, 1000 и т.д. Для этого поочередно будем делить числа из списка (10, 100, 1000) на знаменатель, пока не получим целое число.
10/2 = 5 – целое число;
1. Теперь, путем умножения нашей дроби на полученное число (5), мы преобразовываем нашу дробь в десятичную.
Источник: uchi.ru
1 2 какая дробь
Привет Лёва Середнячок
1,2 перевести в дробь
Комментарии
одна целая две десятых= одна целая одна пятая
Ответ проверен экспертом
5 (1 оценка)
manyny06 7 лет назад
Светило науки — 23372 ответа — 41155 раз оказано помощи
1.2 = 1 2/10 = 1 1/5
ОДНА ЦЕЛАЯ ОДНА ПЯТАЯ
5 (2 оценки)
Kelly5 7 лет назад
Светило науки — 6 ответов — 0 раз оказано помощи
1,2=1 целой и 2/10 ( 1 2/10) но 1 2/10 сокращается на 2, поэтому будет 1 2/10 = 1 1/5
Лучшие помощники
За сегодня
Ежедневный Еженедельный Ежемесячный За 3 месяца
Мозг Отвечающий
Лёва Середнячок
Мозг Отвечающий
Лёва Середнячок
Мозг Отвечающий
Лёва Середнячок
Мозг Отвечающий
Лёва Середнячок
2022 ВашУрок
Этот сайт использует cookies. Политика Cookies Вы можете указать условия хранения и доступ к cookies в своем браузере.
Установи приложение ВашУрок
Источник: vashurok.com
Перевод обыкновенной дроби в десятичную и наоборот
При решении различных вычислительных заданий требуется произвести перевод десятичной дроби в обыкновенную или наоборот. В частности, в бланках ответов первой части ОГЭ (и ЕГЭ) нельзя записывать обыкновенную дробь, так как поле для этой дроби просто не существует. Чтобы перевести обыкновенную дробь в конечную десятичную дробь, необходимо разделить числитель дроби на ее знаменатель. Как перевести обыкновенную дробь в конечную десятичную дробь?
Чтобы перевести обыкновенную дробь в конечную десятичную дробь, необходимо разделить числитель дроби на ее знаменатель (устно или в столбик).
Пример №1. ½ = 0,5 так как 1_2=0,5 Пример №2. ¾ = 0,75 так как 3_4=0,75 Пример №3. Так как 18_25=0,72, то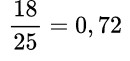 
Если дана смешанная дробь, то целая часть уже есть, делим числитель на знаменатель и добавляем в часть после запятой. Или переводим смешанное число в неправильную дробь и делим числитель на знаменатель.
Строгого правила для способа выполнения данного действия нет. Пример №4.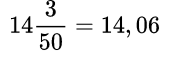 
здесь целая часть 14 уже есть, пишем ее и ставим запятую. Затем делим 3 на 50 и получаем 0,06. Приписываем десятичную часть 06 после запятой к числу 14 и получаем 14,06.
Пример №5. в данном случае сначала перевели смешанное число в неправильную дробь (знаменатель умножается на целую часть и прибавляется числитель – это число записывается в числитель неправильной дроби), а затем разделили числитель 703 на знаменатель 50 и получили 14,06. Как перевести десятичную дробь (конечную) в обыкновенную?
Чтобы перевести десятичную дробь в обыкновенную, нужно в числитель записать цифры из десятичной части дроби (которые стоят после запятой), а в знаменателе написать столько нулей, сколько цифр получилось в числителе. Затем, по возможности сократить данную дробь. Пример №6.
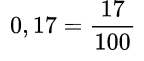целая часть равна нулю, нуль перед обыкновенной дробью не пишется, 17 записали в числитель, а 100 в знаменатель, так как в числе 17 две цифры, как у сотни два нуля. Пример №7.
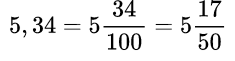целая часть равна 5, поэтому записали ее перед дробью, 34 пошло в числитель, а знаменатель соответственно равен 100 (по количеству цифр в числе 34). Здесь видно, что получилась сократимая дробь, так как числитель и знаменатель оба делятся на 2. Выполняем сокращение дробной части и получаем новую дробь
Задание 7OM21R На координатной прямой отмечены точки А, В, С и D. Одна из них соответствует числу 107 13 . . . Какая это точка?
- точка А
- точка В
- точка С
- точка D
Сначала выразим обыкновенную дробь десятичной, разделив 107 на 13, получаем приближенное число 8,23…. Теперь работаем с числовым лучом, на котором видно, что наше число 8,23.. будет располагаться между числами 8 и 9, но ближе к 8, так как оно меньше 8,5; следовательно, это точка А.
Одно из чисел отмечено на прямой точкой.
Какое это число?
Точка, обозначенная на прямой, лежит между 2 и 3. Т.е. соответствующее ей число больше 1. Это значит, что дробь, которая соответствует этой точке, должна быть неправильной. Но все приведенные в условии дроби неправильные. Чтобы понять, какая из них находится именно на промежутке (2; 3), необходимо выделить их целые части. Та из дробей, у которой целая часть окажется равной 2, и есть искомый результат.
Итак, выделяем целые части:
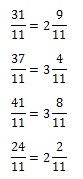
Целую часть, равную 2, имеют две дроби – 1-я и 4-я. Но посмотрим внимательно на прямую. Обозначенная на ней точка находится близко к делению 3. Проанализируем в этом контексте подходящие нам дроби. У первой недостает всего 2/11, чтобы она стала равной 3, между тем как четвертая лишь на 2/11 удалена от деления 2. Следовательно, правильным ответом в данном случае является дробь 31/11. Она соответствует варианту ответа 2.
На координатной прямой отмечена точка А:
Известно, что она соответствует одному из четырёх указанных ниже чисел. Какому из чисел соответствует точка А?
Подход к решению в данной задаче сводится к визуальной оценки имеющихся вариантов на координатной прямой, для этого необходимо предварительно перевести варианты ответов к примерному десятичному виду.
Оцениваем 181/16 – можно поделить 181 на 16, тогда получим 11,3125. Это явно выходит за указанный диапазон, поэтому данный вариант нам не подходит.
Оцениваем √37 – самое близкое значение, из которого вычисляется квадратный корень – это 36, значит √37 – это 6 и что-то еще, что вычислять нам не обязательно. Данное значение нам подходит, так как лежит чуть правее середины отрезка 0-10, как и точка А.
Посмотрим на вариант 0,6 – это явно меньше единицы, а точка А, как мы уже выяснили, лежит в диапазоне 5-10. Данный вариант нам не подойдет.
Вариант с ответом 4 также не подойдет по вышеуказанной причине.
Какое из следующих чисел заключено между числами 8/3 и 11/4 ?
В задании данного типа необходимо выполнить деление 8 на 3 и 11 на 4, то есть перевести дробь из обыкновенного вида в десятичный. Сами дроби могут не иметь представления в десятичном виде, однако в нашем случае достаточно выполнить деление но второго знака после запятой, так как в ответе приведены числа до первого знака после запятой. Итак, выполняем деление:
Получаем значения 2,666.. или 2,(6) и 2,75. Смотрим на варианты ответов и выбираем, соответственно, первый, так как 2,7 находится между 2,(6) и 2,75.
Задание OM0604o Найдите значение выражения: ¼ + 0,07
К данному заданию, как и к большинству заданий 1 модуля Алгебры, подход к решению заключается в переводе дроби от одного вида к другому. В нашем случае это переход от обыкновенной дроби к десятичной.
Переводим ¼ из обыкновенной дроби в десятичную. Делим 1 на 4, получаем 0,25. Затем переписываем выражение с использованием только десятичных дробей и вычисляем:
Задание OM0601o Найдите значение выражения:
Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
Можно произвести вычисления в столбик, тогда получим:
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции – деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
Источник: spadilo.ru
Калькулятор дробей
Выполните сложение, вычитание, умножение, деление и сокращение обыкновенных смешанных и простых дробей и получите решение с правильным ответом.
Что такое дроби?
Дробь – это число, которое состоит из нескольких одинаковых частей — долей единицы, а также из одной ее части.
Обыкновенная дробь выглядит так:
В математической записи дроби число, которое находится выше черты — называется числителем, а число, которое расположено ниже — называется знаменателем. Оно показывает то, на сколько долей разделили единицу.
Первое число является делимым, а второе число служит делителем. Обыкновенные дроби могут образовывать поле рациональных чисел, если они будут с целыми числителями и ненулевыми знаменателями. Они показывают количество долей, на которые делится единица.
Математические дроби начинают изучать в школе. В основном в 5 или в 6 классах. Но также дроби очень часто используются в дальнейшей школьной и затем в вузовской программах.
История дробей
Русское слово «дробь», как и его аналоги в других языках, происходит от латинского слова «fractura» с арабским происхождением и означает в переводе: ломать или дробить. Основы теории обыкновенных дробей заложили греческие и индийские математики. Слова числитель и знаменатель ввёл в оборот греческий математик Максим Плануд.
Позже дроби появляются в Европейской математике, например, у Фибоначчи в 1202 году. Поначалу европейские математики оперировали только с обыкновенными дробями, а в астрономии — с шестидесятеричными. В Европе первые десятичные дроби ввёл Иммануил Бонфис около 1350 года, но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585).
В России, начиная с древней Руси, дроби именовали долями. А в первых отечественных учебниках по математике дроби назывались ломаными числами. Термин «дробь», как аналог латинского «fractura», впервые используется в «Арифметике» Магницкого в 1703 году как для обыкновенных, так и для десятичных дробей.
Виды дробей
Дроби бывают нескольких видов:
- обыкновенные;
- смешанные и простые;
- правильные и неправильные;
- десятичные;
- в виде процентов.
Обыкновенная дробь
Обыкновенная дробь имеет вид a/b. Число a — здесь будет являться числителем дроби, а число b — будет знаменателем.
Правильные и неправильные
Правильной называется дробь, у которой числитель (модуль числителя) меньше модуля знаменателя.
Пример, правильной дроби: 3/4, так как 3
Неправильная дробь, наоборот, имеет числитель, который по модулю больше чем знаменатель.
Пример, неправильной дроби: 4/3, так как 4>3.
Простые и смешанные
Простая дробь содержит только числитель и знаменатель. Например, 4/3.
Смешанная дробь содержит целое число и дробь, и понимается как сумма этого числа и дроби. Например, 1 и 1/3.
Неправильную дробь всегда можно сделать смешанной, то есть выделить в ней целые части.
Десятичная дробь
Десятичная дробь — это запись дроби, в которой знаменатель не дан в явном виде, но понимается как целое число, степень десяти (напр. 10, 100, 1000 и др).
Десятичная дробь записывается через запятую в строку таким образом, чтобы отделить дробную часть от целой части. Вот так:
- 0,7 – ноль целых и 7 десятых (7/10).
- 5,42 – пять целых и 42 сотых (42/100).
- 9,245 – девять целых и 245 тысячных (245/1000).
В виде процентов
Дробь в виде процентов — это когда при переводе десятичной дроби в проценты, ее необходимо умножить на 100. Запись производится с запятыми.
Например, 0,023 = 0,023 * 100% = 2,3%
Для того чтобы перевести проценты в десятичные дроби, следует разделить число процентов на 100.
Что нужно знать, чтобы работать с дробями?
Что переводить дроби из одного вида в другой и выполнять различные операции над дробями, надо знать несколько терминов.
Наименьшее общее кратное (НОК) для нескольких чисел — это наименьшее натуральное число, которое делится на каждое из этих чисел.
Наименьший общий знаменатель – это НОК, которое рассчитывается для знаменателей двух и более дробей.
Как найти наименьший общий знаменатель?
Чтобы это понять, необходимо рассмотреть следующий пример двух дробей:
Если нужно привести дроби с разными знаменателями к общему наименьшему знаменателю, следует найти наименьшее общее кратное (НОК) знаменателей этих дробей.
Знаменатель первой дроби равен 20.
Его нужно разложить его на простые множители: 20=2⋅5⋅2.
Далее также разложить 2 знаменатель дроби 14 на простые множители: 14 = 7*2.
Убираем повторяющиеся множители у знаменателя второй дроби и получаем:
НОК (14,20) = 2*5*2*7 = 140.
В итоге общий наименьший знаменатель равняется 140.
Как привести дробь к общему знаменателю?
Берем первую дробь 1/20 и умножаем ее на 7, чтобы прийти к 140. Для этого умножаем числитель и знаменательно на 7 и получаем:
А вторую дробь теперь следует умножить на 10 таким же образом:
Общим наибольшим делителем (НОД) нескольких чисел является самое большее целое натуральное число, на которое эти самые числа делятся без остатка.
Общий наибольший делитель обозначается в виде такой записи: НОД (18; 48) = 6.
Как следует переводить дробь?
Из смешанной дроби в обыкновенную:
- Необходимо умножить знаменатель дробной части на единицу целой части;
- К произведению, которое получилось, следует прибавить числитель дробной части;
- Сам знаменатель при этом оставить без изменений.
Из обыкновенной дроби в смешанную:
- Разделить числитель дроби на знаменатель;
- Полученный результат будет являться целой частью;
- То, что останется в результате деления (остаток) будет числителем.
Из десятичной дроби в обыкновенную или смешанную^
- Для этого действия необходимо целую часть умножать на знаменатель дробной части.
- После этого полученный результат сложить с числителем дробной части. То, что получилось в итоге, и будет числителем новой дроби, а сам знаменатель при этом останется без изменений.
Операции над дробями
С дробями можно совершать различные арифметические операции.
➕ Сложение
Для сложения дробей с разными знаменателями сначала нужно найти знаменатель, который является общим. После этого нужно к общему знаменателю привести дроби. Хорошо, если это будет наименьший знаменатель.
Далее — выполнить сложение дробей, где под суммой числителей подписать общий знаменатель.
В конце, если возможно, сократить полученную дробь.
➖ Вычитание
Здесь потребуется из числителя уменьшаемого отнять числитель вычитаемого, а сам знаменатель при этом оставить без изменений.
Так, чтобы сделать вычитание из дроби, следует сначала вычесть числители, а все одинаковые знаменатели оставлять прежними.
✖ Умножение
Для этого умножаются числители и записывается результат, как числитель дроби.
Далее, умножаются знаменатели и записывается результат, как знаменатель дроби.
➗ Деление
Здесь следует числитель первой дроби умножить на знаменатель второй дроби. После чего записать полученное произведение в числитель новой дроби.
Знаменатель первой дроби умножается на числитель второй дроби. Далее записывается произведение, как знаменатель новой дроби.
Сокращение
Это действие получается тогда, когда необходимо разделить числитель и знаменатель на одинаковое число, но которое не может быть равно 0.
В итоге получается равную дробь, имеющая меньший знаменатель и числитель.
Чтобы сократить дробь, необходимо в определенной последовательности проверять, на что делятся знаменатель и числитель. В случае, когда находится общий делитель, то сокращать именно на него.
Значительно упростит сокращение раскладывание знаменателя и числителя на множители.
❓ Вопросы и ответы
А также советуем обратить внимание на некоторые часто задаваемые вопросы про дроби и ответы на них.
Какие дроби называются простыми?
Простые дроби — это те, которые записываются в виде 2-ух целых чисел, определенных скошенной или горизонтальной прямой. Например: 1/4,1/2.
Какие дроби называются десятичными?
Когда в знаменателях стоят 10, 100, 1000 и т.д. и степень числа 10, то дроби имеют название — десятичные.
Какие дроби называются правильными?
Правильные дроби те, у которых модуль знаменателя больше модуля числителя.
Какие дроби называются неправильными?
Неправильные дроби те, у которых модуль числителя меньше, чем модуль знаменателя.
Как разделить дробь на дробь?
Нельзя делить на 0.
Если делить на 1 — будет такое же число.
Если делить 0 на любое число, получится 0.
Какая дробь называется положительной?
Когда она больше 0.
Какая дробь называется отрицательной?
Когда перед положительной дробью ставится знак «–».
Что такое степени с дробями?
Степени с дробями приводятся к знаменателю так же, как и рациональные дроби. Нужно найти дополнительный множитель и умножить на него знаменатель и числитель дроби.
При этом дополнительный множитель подбирать так, чтобы он не обращался в 0 для исходящего выражения.
Как пользоваться калькулятором дробей?
Калькулятор, решающий дроби, позволяет переводить дроби и производить самые простые операции типа сложения, вычитания, умножения, деления.
Для этого нужно заполнить соответствующие поля для дробей и нажать кнопку «Вычислить».
Поделитесь в соцсетях
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Источник: ecalc.ru