![]()
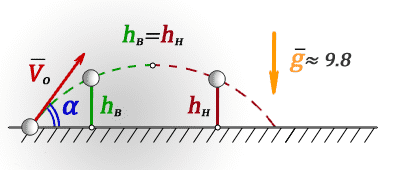
Таким образом, одному значению высоты будет соответствовать два значения времени, одно при подъеме, второе при падении.
2. Найти время полета тела пролетевшее определенное расстояние
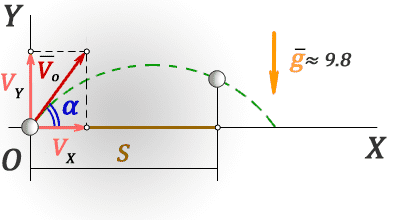
S — расстояние пройденное по горизонтали
t — время за которое тело прошло расстояние S
Vo — начальная скорость тела
Vx — проекция начальной скорости на ось OX
Vy — проекция начальной скорости на ось OY
α — угол под которым брошено тело
g ≈ 9,8 м/с 2 — ускорение свободного падения
Задачки про часовые пояса и время прилета самолетов
Формула для определения значения времени , за которое пройдено определенное расстояние
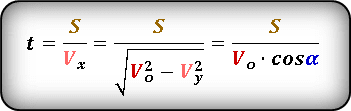
3. Значение времени при максимальных значениях высоты и дальности
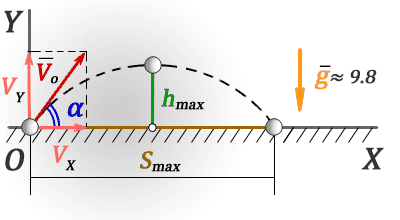
Smax — максимальная дальность по горизонтали
hmax — максимальная высота
tmax — время всего полета
th — время за которое тело поднялось на максимальную высоту
Vo — начальная скорость тела
Vx — проекция начальной скорости на ось OX
Vy — проекция начальной скорости на ось OY
α — угол под которым брошено тело
g ≈ 9,8 м/с 2 — ускорение свободного падения
Формула для определения значения времени , затраченное на весь полет, если известна начальная скорость или ее проекции
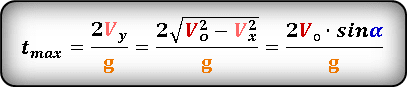
Формула для определения значения времени , на максимальной высоте
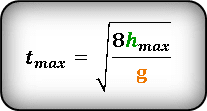
![]()
Т. к. траектория движения тела симметрична относительно линии максимальной высоты, следовательно — время всего полета, в два раза больше времени затраченного при подъеме на максимальную высоту
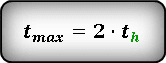
Определение путевой скорости и угла сноса
Источник: www-formula.ru
Описание баллистического движения. Расчет времени полета.
Франчайзинг Эффективные формы международного предпринимательства Для организации международной деятельности фирме потребуется проанализировать.
Предметно-количественный учет спирта этилового в медицинской организации Тема: Оборот лекарственных средств Источник: Электронная система «Контроль в ЛПУ» Этиловый спирт не относится к НС и ПВ и включен в.
Конституционные основы местного самоуправления в Российской Федерации Местное самоуправление как выражение власти народа составляет одну из основ конституционного строя РФ.
Виды ионизирующих излучений Ионизирующие излучения Ионизирующее излучение — это любое излучение, вызывающее ионизацию среды,т.
Ответы к заданиям для выполнения практической задачи по дисциплине «Товароведение продовольственных товаров» Вопрос № 1 Определить товарный сорт масло Крестьянского по органолептическим показателям: масло имеет чистые.
Сейчас читают про:







Источник: studopedia.ru
Движение тела, брошенного горизонтально
Движение тела, брошенного горизонтально — это сложное движение по криволинейной траектории, которое можно представить как сумму двух независимых друг от друга движений — равномерного прямолинейного движения по горизонтали и свободного падения по вертикали.
Основные характеристики и формулы
Для кинематического описания движения выберем систему координат, как показано на рис.1, и запишем законы изменения кинематических характеристик движения тела для каждого из направлений.
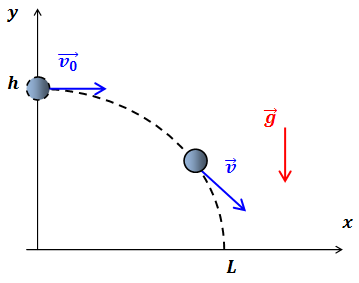
Рис.1. Движение тела, брошенного горизонтально
По горизонтали (вдоль оси ):
начальное положение , начальная скорость , скорость ускорение закон движения:
По вертикали (вдоль оси ):
начальное положение , начальная скорость , скорость ускорение закон движения:
Используя приведенные выше законы движения, можно найти время и дальность полета тела.
В точке падения — координата тела равна нулю, поэтому можно записать:
откуда время полета:
— координата тела в точке падения равна дальности полета и является расстоянием, пройденным телом вдоль оси за время :
Знание законов изменения координат тела с течением времени позволяет рассчитать траекторию тела. Выразив время из закона движения вдоль горизонтального направления:
подставим это выражение в закон движения вдоль вертикального направления и получим уравнение траектории тела:
Полученное уравнение траектории показывает, что тело, брошенное горизонтально, двигается по параболе, вершина которой находится в точке бросания.
Примеры решения задач
| Задание | Камень бросили горизонтально с некоторой высоты. Через его скорость оказалась направлена под углом к горизонту. Чему равна начальная скорость камня. |
| Решение | Выберем систему координат, как показано на рисунке. |
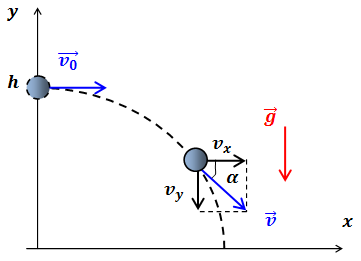
Представим сложное криволинейное движение в виде суммы независимых движений в горизонтальном и вертикальном направлениях и запишем законы изменения со временем горизонтальной и вертикальной компонент вектора скорости:
(горизонтальная составляющая вектора скорости не зависит от времени);
Горизонтальная составляющая вектора скорости — это проекция вектора скорости на ось , поэтому:
Приравнивая правые части соотношений для скорости тела, получим:
Воспользуемся тригонометрической формулой:
откуда начальная скорость тела:
Ускорение свободного падения м/с .
Подставив в формулу численные значения физических величин, получим:
| Задание | Из двух пунктов отвесного берега. находящихся на некоторой высоте от поверхности воды, одновременно бросают в горизонтальном направлении два тела. Начальные скорости тел 5 и 7,5 м/с . Оба тела падают в воду одновременно. Расстояние от берега до точки падения первого тела в воду 10 м. Определить: 1) продолжительность полета тел; 2) высоту, с которой они были брошены; 3) место падения второго тела в воду. |
| Решение | Выберем систему координат, как показано на рисунке. |
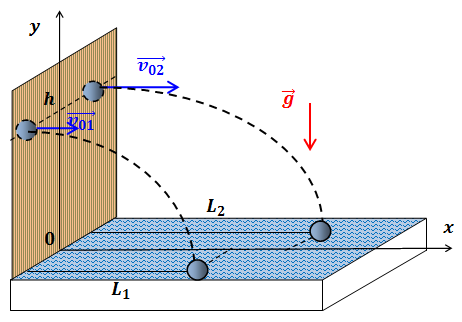
Запишем законы движения для обоих тел:
По условию задачи первое тело упало в воду на расстоянии поэтому продолжительность полета первого тела также, как и второго тела 9по условию они равны) можно найти из соотношения:
В момент падения первого тела его — координата равна нулю, поэтому:
откуда высота, с которой было брошено тело:
Дальность полета второго тела определим, положив в момент падения — координату равной
Источник: ru.solverbook.com
Движение тела, брошенного под углом к горизонту!

До конца финального матча баскетбольного турнира Олимпиады в Мюнхене 1972-ого года оставалось 3 секунды. Американцы – сборная США — уже во всю праздновали победу! Наша команда – сборная СССР – выигрывала около 10-и очков у великой dream Team.
. за несколько минут до окончания матча. Но, растеряв в концовке все преимущество, уже уступала одно очко 49:50. Дальше произошло невероятное! Иван Едешко бросает мяч из-за лицевой линии через всю площадку под кольцо американцев, где наш центровой Александр Белов принимает мяч в окружении двух соперников и вкладывает его в корзину. 51:50 – мы олимпийские чемпионы.
Я, будучи тогда ребенком, испытал сильнейшие эмоции – сначала разочарование и обиду, затем сумасшедший восторг! Эмоциональная память об этом эпизоде врезалась в мое сознание на всю жизнь! Посмотрите видео в Интернете по запросу «золотой бросок Александра Белова», не пожалеете.
Американцы тогда не признали поражения и отказались от получения серебряных медалей. Возможно ли за три секунды сделать то, что совершили наши игроки? Вспомним физику!
В этой статье мы рассмотрим движение тела, брошенного под углом к горизонту, составим в Excel программу решения этой задачи при различных сочетаниях исходных данных и попытаемся ответить на поставленный выше вопрос.
Это достаточно широко известная задача в физике. В нашем случае тело, брошенное под углом к горизонту – это баскетбольный мяч. Мы рассчитаем начальную скорость, время и траекторию полета мяча, брошенного через всю площадку Иваном Едешко и попавшего в руки Александра Белова.
Математика и физика полета баскетбольного мяча.
Представленные ниже формулы и расчет в excel являются универсальными для широкого круга задач о телах, брошенных под углом к горизонту и летящих по параболической траектории без учета влияния трения о воздух.
Расчетная схема представлена на рисунке, расположенном ниже. Запускаем программу MS Excel или OOo Calc.

Исходные данные:
1. Так как мы находимся на планете Земля и рассматриваем баллистическую задачу – движение тел в поле тяжести Земли, то первым делом запишем основную характеристику гравитационного поля – ускорение свободного падения g в м/с 2
в ячейку D3: 9,81
2. Размеры баскетбольной площадки – 28 метров длина и 15 метров ширина. Расстояние полета мяча почти через всю площадку до кольца от противоположной лицевой линии по горизонтали x в метрах впишем
в ячейку D4: 27,000
3. Если принять, что бросок Едешко совершил с высоты около двух метров, а Белов поймал мяч как раз где-то на уровне кольца, то при высоте баскетбольного кольца 3,05 метра расстояние между точками вылета и прилета мяча составит по вертикали 1 метр. Запишем вертикальное перемещение y в метрах
в ячейку D5: 1,000
4. По моим замерам на видеозаписи угол вылета мяча α0 из рук Едешко не превышал 20°. Введем это значение
в ячейку D6: 20,000

Результаты расчетов:
Основные уравнения, описывающие движение тела, брошенного под углом к горизонту без учета сопротивления воздуха:
x = v0 *cos α0 * t
y = v0 *sin α0 * t — g * t 2 /2
5. Выразим время t из первого уравнения, подставим во второе и вычислим начальную скорость полета мяча v0 в м/с
в ячейке D8: =(D3*D4^2/2/COS (РАДИАНЫ(D6))^2/(D4*TAN (РАДИАНЫ (D6)) -D5))^0,5 =21,418
v0 =( g * x 2 /(2*(cos α0 ) 2 *( x *tg α0 — y )) 0,5
6. Время полета мяча от рук Едешко до рук Белова t в секундах рассчитаем, зная теперь v0 , из первого уравнения
в ячейке D9: =D4/D8/COS (РАДИАНЫ(D6)) =1,342
t = x /( v0 *cos α0 )
7. Найдем угол направления скорости полета мяча αi в интересующей нас точке траектории. Для этого исходную пару уравнений запишем в следующем виде:
y = x *tg α0 — g * x 2 /(2* v0 2 *(cos α0 ) 2 )
Это уравнение параболы – траектории полета.
Нам необходимо найти угол наклона касательной к параболе в интересующей нас точке – это и будет угол αi . Для этого возьмем производную, которая представляет собой тангенс угла наклона касательной:
y’ =tg α0 — g * x /( v0 2 *(cos α0 ) 2 )
Рассчитаем угол прилета мяча в руки Белова αi в градусах
в ячейке D10: =ATAN (TAN (РАДИАНЫ(D6)) -D3*D4/D8^2/COS (РАДИАНЫ (D6))^2)/ПИ()*180 =-16,167
αi = arctg y ’ =arctg(tg α0 — g * x /( v0 2 *(cos α0 ) 2 ))
Расчет в excel, в принципе, закончен.
Иные варианты расчетов:
Используя написанную программу, можно быстро и просто при других сочетаниях исходных данных произвести вычисления.
Пусть, даны горизонтальная x =27 метров, вертикальная y =1 метр дальности полета и начальная скорость v0 =25 м/с.
Требуется найти время полета t и углы вылета α0 и прилета αi
Воспользуемся сервисом MS Excel «Подбор параметра». Я неоднократно в нескольких статьях блога подробно рассказывал, как им пользоваться. Детальнее об использовании этого сервиса можно почитать здесь.
Устанавливаем в ячейке D8 значение 25,000 за счет изменения подбором значения в ячейке D6. Результат на рисунке внизу.
Исходные данные в этом варианте расчета в excel (как, впрочем, и в предыдущем) выделены синими рамками, а результаты обведены красными прямоугольными рамками!

Устанавливая в таблице Excel некоторое интересующее значение в одной из ячеек со светло-желтой заливкой за счет подбора измененного значения в одной из ячеек со светло-бирюзовой заливкой, можно получить в общем случае десять различных вариантов решения задачи о движении тела, брошенного под углом к горизонту при десяти разных наборах исходных данных.
Ответ на вопрос:
Ответим на вопрос, поставленный в начале статьи. Мяч, посланный Иваном Едешко, долетел до Белова по нашим расчетам за 1,342с. Александр Белов поймал мяч, приземлился, подпрыгнул и бросил. На все это у него было «море» времени – 1,658с! Это действительно достаточное с запасом количество времени!
Детальный просмотр по кадрам видеозаписи подтверждает вышесказанное. Нашим игрокам хватило трех секунд, чтобы доставить мяч от своей лицевой линии до щита соперников и забросить его в кольцо, вписав золотом свои имена в историю баскетбола!
Прошу уважающих труд автора скачивать файл после подписки на анонсы статей!
Статьи с близкой тематикой
- Теплофизические свойства воздуха
- Теплофизические свойства воды
- Солнечная энергия
- Настенные солнечные часы
- Ветровая нагрузка
Источник: al-vo.ru