Вы можете использовать этот инструмент для получения наиболее упрощенного соотношения или для сравнения двух одинаковых соотношений.
Соотношение
Соотношение в математике — это термин, который используется для сравнения двух или более чисел. Он используется, чтобы указать, насколько велика или мала величина по сравнению с другой. В отношении две величины сравниваются с помощью деления. Здесь делимое называется «антецедентом», а делитель — «консеквентом».
Например, в группе из 30 человек 17 из них предпочитают ходить по утрам, а 13 — ездить на велосипеде. Чтобы представить эту информацию в виде соотношения, запишем его как 17:13. Здесь символ ‘:’ читается как «есть к». Таким образом, отношение людей, предпочитающих ходить пешком, к людям, предпочитающим езду на велосипеде, читается как «17 к 13».
Что такое соотношение?
Соотношение определяется как сравнение двух величин в одних и тех же единицах измерения, которое показывает, сколько одного количества присутствует в другом количестве. Коэффициенты можно разделить на два типа. Одно из них — соотношение части к части, а другое — соотношение части к целому. Соотношение частей к частям показывает, как связаны две различные сущности или группы.
Урок 1. Закон и законность: понятие и соотношение
Например, соотношение мальчиков и девочек в классе составляет 12: 15, тогда как соотношение частей к целому обозначает соотношение между определенной группой и целым. Например, из каждых 10 человек 5 любят читать книги. Таким образом, соотношение части к целому составляет 5: 10, что означает, что каждые 5 человек из 10 любят читать книги.
Формула соотношения

Мы используем формулу соотношения при сравнении соотношения между двумя числами или величинами. Общая форма представления соотношения между двумя величинами, скажем, «a» и «b», — это a: b, которое читается как «a равно b». Форма дроби, представляющая это соотношение, — a/b.
Чтобы еще больше упростить соотношение, мы следуем той же процедуре, которую используем для упрощения дроби. a:b = a/b. Давайте разберемся в этом на примере. Пример. В классе из 50 учеников 23 девочки, а остальные мальчики. Найдите соотношение количества мальчиков к количеству девочек.
Общее количество студентов = 50; Количество девушек = 23. Общее количество мальчиков = Общее количество учеников — Общее количество девочек
= 50 — 23
= 27 Таким образом, желаемое соотношение (Количество мальчиков: Количество девочек) равно 27:23.
Расчет коэффициентов
- Шаг 1: Найдите величины обоих сценариев, для которых мы определяем соотношение. В данном случае это 15 и 20.
- Шаг 2: Запишите его в форме дроби a /b. Итак, мы записываем это как 15/20.
- Шаг 3: По возможности еще больше упростите дробь. Упрощенная дробь даст окончательное соотношение. Здесь 15/20 может быть упрощено до 3/4.
- Шаг 4: Поэтому соотношение муки к сахару можно выразить как 3:4.
Используйте бесплатный онлайн-калькулятор коэффициентов, чтобы проверить свои ответы при расчете коэффициентов.
Отношение двух чисел. 6 класс.
Как упростить соотношения?
Соотношение выражает, сколько требуется одного количества по сравнению с другим количеством. Два термина в соотношении могут быть упрощены и выражены в их низшей форме. Соотношения, выраженные в их наименьших выражениях, легко понять и могут быть упрощены так же, как мы упрощаем дроби. Чтобы упростить соотношение, мы используем следующие шаги.
Давайте разберемся в этом на примере. Например, давайте упростим соотношение 18:10.
- Шаг 1: Запишите заданное соотношение a:b в виде дроби a/b. Записав соотношение в виде дроби, мы получим 18/10.
- Шаг 2: Найдите наибольший общий коэффициент ‘a’ и ‘b’. В этом случае GCF из 10 и 18 равен 2.
- Шаг 3: Разделите числитель и знаменатель дроби на GCF, чтобы получить упрощенную дробь. Здесь, разделив числитель и знаменатель на 2, мы получаем, (18÷2)/(10÷2) = 9/5.
- Шаг 4: Представьте эту дробь в форме соотношения, чтобы получить результат. Таким образом, упрощенное соотношение составляет 9:5.
Используйте бесплатный онлайн-калькулятор коэффициентов упрощения, чтобы проверить свои ответы.
Советы и рекомендации по соотношению:
- В случае, если оба числа «a» и «b» равны в соотношении a: b, то a: b = 1.
- Если a > b в соотношении a : b, то a : b > 1.
- Если a < b в соотношении a : b, то a : b < 1.
- Перед их сравнением необходимо убедиться в том, что единицы измерения двух величин одинаковы.
Эквивалентные Соотношения
Эквивалентные соотношения аналогичны эквивалентным дробям. Если предшествующий (первый член) и последующий (второй член) данного соотношения умножаются или делятся на одно и то же число, отличное от нуля, это дает эквивалентное соотношение.
Например, когда антецедент и следствие соотношения 1:3 умножаются на 3, мы получаем, (1 × 3) : (3 × 3) или 3: 9. Здесь 1:3 и 3:9 являются эквивалентными соотношениями. Аналогично, когда оба члена соотношения 20:10 делятся на 10, это дает 2:1. Здесь 20:10 и 2:1 являются эквивалентными соотношениями. Бесконечное число эквивалентных соотношений любого заданного соотношения может быть найдено путем умножения предшествующего и последующего на положительное целое число.
Таблица коэффициентов
Таблица коэффициентов — это список, содержащий эквивалентные коэффициенты любого заданного соотношения в структурированном виде. В следующей таблице соотношений приведено соотношение между соотношением 1:4 и четырьмя его эквивалентными соотношениями. Эквивалентные соотношения связаны друг с другом умножением числа. Эквивалентные соотношения получаются путем умножения или деления двух членов соотношения на одно и то же число. В примере, показанном на рисунке, давайте возьмем соотношение 1:4 и найдем четыре эквивалентных соотношения, умножив оба члена соотношения на 2, 3, 6 и 9. В результате мы получаем 2:8, 3:12, 6:24, и 9:36.
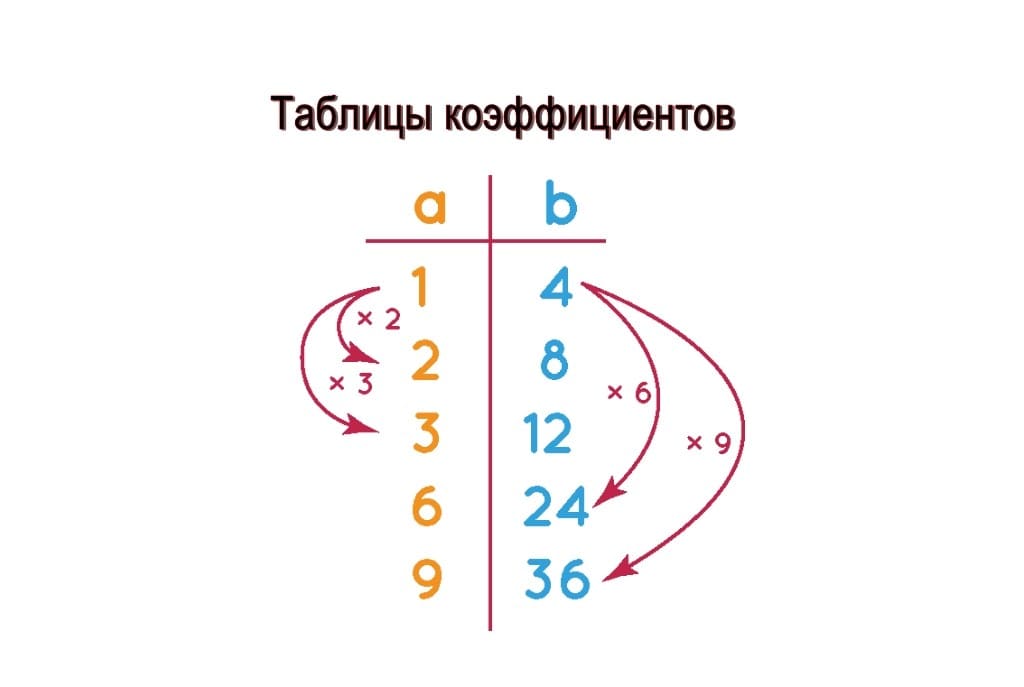
Используйте бесплатный онлайн-калькулятор эквивалентных коэффициентов, чтобы проверить свои ответы.
Примеры соотношения
- Пример 1. В школьном зале 49 мальчиков и 28 девочек. Выразите соотношение числа мальчиков к числу девочек. Решение: Учитывая, что количество мальчиков = 49, а количество девочек = 28. GCF 49 и 28 равен 7. Теперь, для упрощения, разделите два термина на их GCF, который равен 7. Это означает, (49 ÷ 7)/(28 ÷ 7) = 7/4. Следовательно, соотношение числа мальчиков к числу девочек = 7:4.
- Пример 2: В музыкальном классе 30 учеников. 10 из них были взрослыми, а остальные — детьми. Каково соотношение числа детей к общему числу учащихся в музыкальном классе? Решение: Учитывая, что общее количество учащихся в музыкальном классе = 30, а общее количество взрослых = 10. Следовательно, количество детей, посещавших музыкальный класс = 30 -10, что равно 20. Отношение общего числа детей к общему числу учащихся в музыкальном классе = 20: 30, что в упрощенном виде дает 2:3.
- Пример 3: Упростите заданное соотношение, 87:75. Решение: Чтобы упростить данное соотношение, мы сначала найдем GCF 87 и 75, что равно 3. Затем мы разделим каждый член на 3. Это означает, (87 ÷ 3)/(75 ÷ 3) = 29/25. Таким образом, соотношение 87:75 в простейшей форме равно 29:25.
Как ваш ребенок может овладеть математическими понятиями?
Математическое мастерство приходит с практикой и пониманием того, «Почему» стоит за «Что». Почувствуйте разницу в математике.
Источник: www.sas.com.ru
Пропорция 1 к 1 это как?
Вы можете войти или зарегистрироваться, чтобы добавить ответ и получить бонус.
Лучшие предложения
- Бывает ли у кошек аллергия на людей?
- В честь кого были названы конфеты Mhttps://vamber.ru/question/proporciya-1-k-1-eto-kak/» target=»_blank»]vamber.ru[/mask_link]
Прямая и обратная пропорциональность
Чем старше дерево, тем оно выше. Чем медленнее темп, тем дольше идти до школы. Эти и другие процессы можно описать математическим языком в виде прямой и обратной пропорциональной зависимости. Как это делать — расскажем в этой статье.
24 декабря 2020
· Обновлено 28 октября 2022
Основные определения
Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.
- Прямая зависимость. Чем больше одна величина, тем больше вторая. Чем меньше одна величина, тем меньше вторая величина.
- Обратная зависимость. Чем больше одна величина, тем меньше вторая. Чем меньше одна величина, тем больше вторая.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.
Есть две разновидности пропорциональностей:
- Прямая пропорциональность. Это зависимость, при которой увеличение одного числа ведет к увеличению другого во столько же раз. А уменьшение одного числа ведет к уменьшению другого во столько же раз.
- Обратная пропорциональность. Это зависимость, при которой уменьшение одного числа ведет к увеличению другого во столько же раз. А увеличение числа наоборот ведет к уменьшению другого во столько же раз.
Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Пройти урок
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».
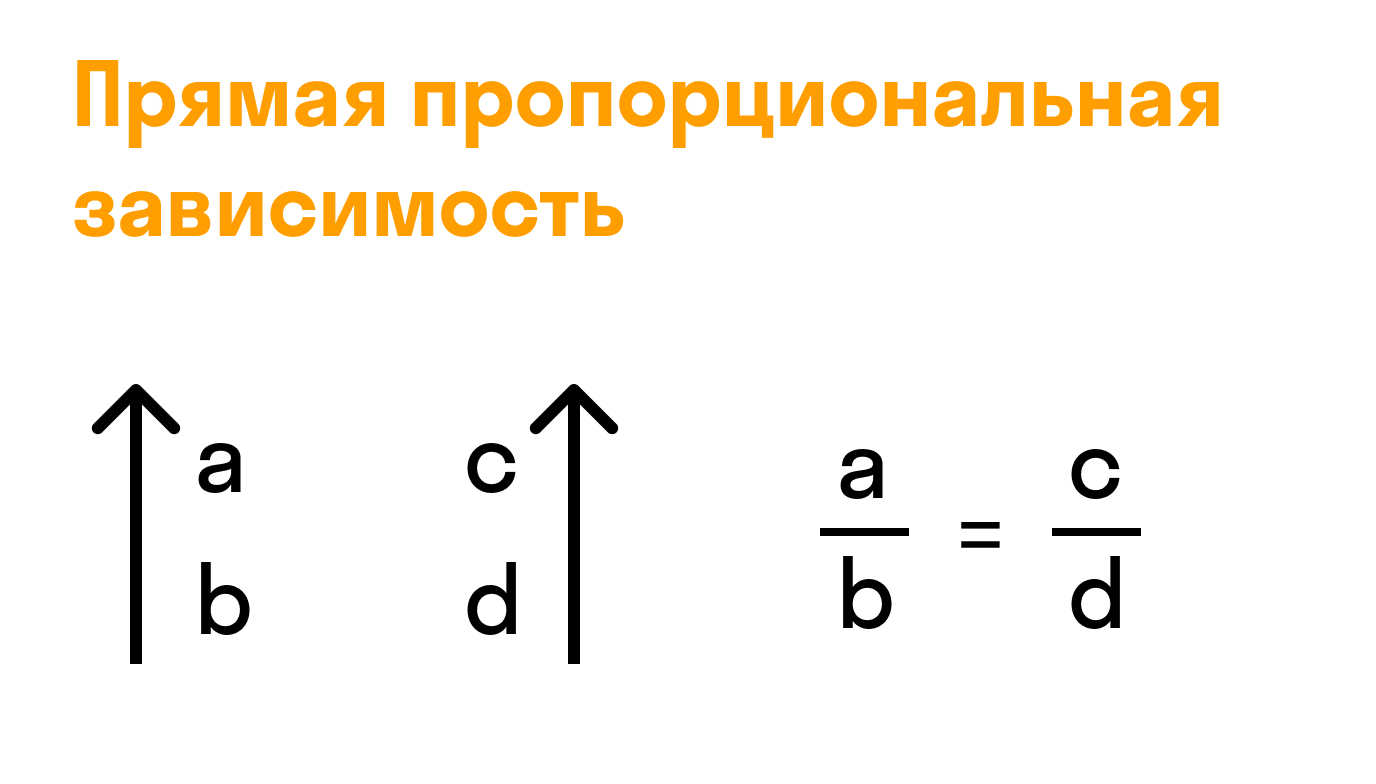
a и d называются крайними членами, b и c — средними.
Основное свойство пропорции
Произведение крайних членов равно произведению средних членов.Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
- при постоянной скорости пройденный маршрут прямо-пропорционально зависит от времени;
- периметр квадрата и его сторона — прямо-пропорциональные величины;
- стоимость конфет, купленных по одной цене, прямо-пропорционально зависит от их количества.
Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
Формула прямой пропорциональности
y = kx,
где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
- Вспомним формулу для определения пути через скорость и время:
- Так как оба автомобиля проделали одинаковый путь, можно составить пропорцию из двух выражений:
- Найдем скорость второго автомобиля:
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней, если они пишут с такой же скоростью?
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
- Составим пропорцию: 14 (постов) / 8 (дней) × х (блогеров) = 420 (постов) / 12 (дней)
- Вспомним основное свойство пропорции, согласно которому: 14x × 12 = 420 × 8 х = (420 × 8) / (14 × 12)
- х = 20
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратно пропорциональные величины
Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.
Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».
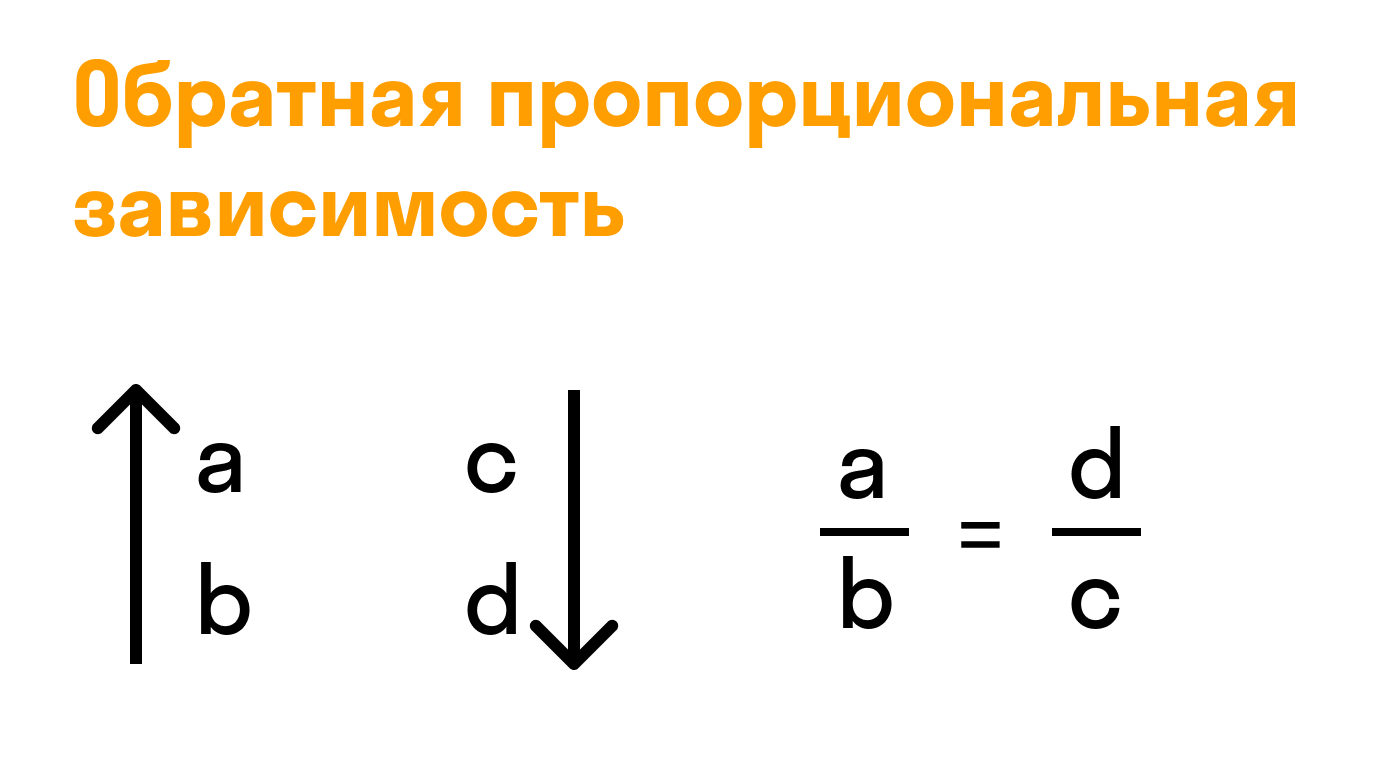
Свойство обратной пропорциональности величин:
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Примеры обратно пропорциональной зависимости:
- время на маршрут и скорость, с которой путь был пройден — обратно пропорциональные величины;
- при одинаковой продуктивности количество школьников, решающих конкретную задачу, обратно пропорционально времени выполнения этой задачи;
- количество конфет, купленных на определенную сумму денег, обратно пропорционально их цене.
Формула обратной пропорциональности
где y и x — это переменные величины,
k — постоянная величина, которую называют коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Записаться на интенсив

Потренируемся
Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
- В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
- Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.
- Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:

- Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию: 30 : 24 = 5 : х
- Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член: х = 24 * 5 : 30 х = 4
- Значит, 30 человек раскрутят канал за 4 дня.
Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
- Составим пропорцию: Соотношения равны, но перевернуты относительно друг друга.
- Подставим известные значения: Ответ: 18 часов 45 минут.
Источник: skysmart.ru
О соотношении 3:1
Текст написан при моем незначительном соучастии, оригинал здесь: http://www.diary.ru/~a-nor/p61244620.htm.
Многие из тех, кто хоть немного интересуется военным делом, наверняка слышали про «соотношение 3:1 в наступлении». Слышать-слышали, а понимает всяк по своему. Порой — диаметрально противоположно. Одни скажут, что это соотношение, требуемое для успешной атаки, другие, напротив, что при таком раскладе можно благополучно обороняться — типа «против 800 немецких танков нам достаточно 266 своих». Последнее еще и путает тактику с оперативным искусством, внося окончательную сумятицу.
Между тем, цифра такая в учебнике тактики правда есть. И имеет вполне конкретное значение.
Открываем книгу «Тактика: взвод, отделение, танк» 1985 года издания. И обнаруживаем там табличку потерь в наступлении в зависимости от соотношения плотностей огня сторон.
Что это такое? Вообще, в бою важна не столько сама численность, сколько количество пуль, которые подразделение во врага способно выпустить (хотя оно, естественно, зависит от числа людей с оружием). Сейчас будет немножко математики. Боевая скорострельность автомата Калашникова — 100 выстрелов в минуту.
Таким образом, автоматчик, чье отделение наступает на фронте в 100 метров длиной, выпускает 1 пулю на метр фронта в минуту. Посчитав всех бойцов с учетом характеристик их оружия, находим общую плотность огня и сравниваем с вражеской.
(зачем так сложно? Потому что, к примеру, два пулеметчика создают такую же плотность огня, как пять автоматчиков. Так что просто по головам считать будет неверно).
Итак. При плотности огня наступающих втрое больше, чем у обороняющихся, к моменту выхода к переднему краю потери атакующих составят 49% от исходной численности, а защищающихся — 56%. (для сравнения: при соотношении 2:1 они составят, соответственно, 88 и 28 процентов). То есть, 3:1 — это то соотношение, при котором наступающие, добежав до вражеских позиций, еще будут из себя что-то представлять, как боевая сила. Опять же, для сравнения, наступление при соотношении 4:1 гораздо приятнее: потери атакующих будут 30%, обороняющихся — 84%. Ну, а если уж удалось собрать шестикратное превосходство в огневой мощи, то наступающие, потеряв каждого десятого, полностью истребят обороняющихся и войдут в опустевшие окопы.
(Это, кстати, к вопросу о «нехорошо воевать людскими массами». Значительное численное преимущество, как видим, при прочих равных снижает потери)
Необязательно, впрочем. собирать толпу. В учебнике прямо сказано, что добиваться благоприятного соотношения можно и нужно, перед атакой уменьшив число противников с помощью артиллерийской подготовки. И тут мы подходим к проблеме. Уже на уровне батальонов «три к одному» начинает поскрипывать.
Пока мы мерялись с противником повзводно, все было нормально. Роты с ротами — тоже ничего. А вот у батальонов появляется собственная артиллерия — в виде минометных батарей. Теперь представим, что на один батальон с 6 минометами наступает три батальона с, соответственно, 18 минометами. Что произойдет дальше?
Артиллерия наступающих, пользуясь численным перевесом, подавит орудия противника — а затем начнет совершенно безнаказанно гвоздить по его пехоте. Всех, конечно, не перебьет, но нехороший перевес создаст. И выше по армейской иерархии, когда появляются уже артдивизионы с большими пушками, от разницы в численности будет становиться ве хуже и хуже. Если у нас обороняется 7 дивизий против 21 вражеской (как было в 1941 году в Белоруссии, в полосе обороны 4-й армии), это не «один к трем достаточно для обороны», это гарантированный коллапс армии. В 44-м там же хватило двойного людского превосходства (правда, при сокрушительном техническом).
Другой пункт, опрокидывающий рассуждения о достаточности для обороны 1/3 от численности неприятельских войск — это стратегическая инициатива. Если 1/3 довольно для спокойного сидения в окопах, ничто не помешает сильнейшей стороне сконцентрировать на нужном участке этак в шесть-семь раз больше солдат и техники, и просто задавить защищающегося. А после такого прорыва фронта слабейшей стороне придется бросать любовно вырытые окопы и отступать, надеясь уйти из намечающегося мешка скорее, чем пути отхода будут перерезаны.
Окопы полного профиля, бункера, мины и прочая колючая проволока могут дать, выражаясь терминологией компьютерных игр, «бонус при атаке пехоты». Даже танков.
Но когда речь идет об артиллерийской дуэли, никаких преимуществ оборона не дает — при равном техническом оснащении и подготовке исход контрбатарейной борьбы, скорее всего, решать будет просто количество стволов (при прочих равных). Тем более, это справедливо для борьбы авиационных группировок. Так что полководцу не стоит льстить себя надеждой, что активная работа лопатами защитит от втрое (и даже вдвое) больших сил противника. Для успешной обороны реально желательно численное равенство. Хотя бы в артиллерии.
Источник: p-chuchundrin.livejournal.com
23 985 заявок