Если вы не купаетесь только из-за страха утонуть — эта статья для вас. В ней разбираемся с тем, почему тела в принципе плавают. Пригодится не только на физике, но и чтобы меньше бояться воды. Поплыли!
· Обновлено 28 октября 2022
Сила: что это за величина
Перед тем, как разобраться в процессе плавания тел, нужно понять, что такое сила.
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причина любого действия или взаимодействия — ее величество сила.
- Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — единице измерения, которую назвали в честь Исаака Ньютона.
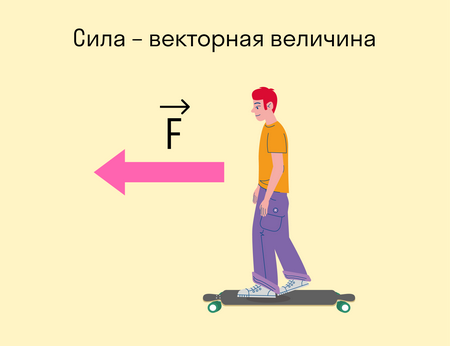
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В этом случае результат выражается в направлении движения.
За СЕКУНДУ ДО… Самые Жуткие КРУШЕНИЯ Кораблей, Снятые на Камеру
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Закон Архимеда
Этот закон известен преимущественно не своей формулировкой, а историей его возникновения.
Легенда гласит, что царь Герон II попросил Архимеда определить, из чистого ли золота сделана его корона, при этом, не причиняя вреда самой короне. То есть, нельзя ее расплавить или в чем-нибудь растворить.
Взвесить корону Архимеду труда не составило, но этого было мало — нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото.
Это можно сделать по формуле плотности.
Формула плотности тела
ρ — плотность тела [кг/м 3 ]
m — масса тела [кг]
V — объем тела [м 3 ]
Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему.
Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый закричал «Эврика!» и побежал докладывать о своей победе в царский дворец (по легенде он даже не оделся).
Выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю весу вытесненной жидкости и противоположно ему направлена.
За СЕКУНДУ ДО… Самые Жуткие КРУШЕНИЯ Кораблей, Снятые на Камеру
На поверхность твердого тела, погруженного в жидкость или газ, действуют силы давления. Эти силы увеличиваются с глубиной погружения, и на нижнюю часть тела будет действовать со стороны жидкости большая сила, чем на верхнюю.
Равнодействующая всех сил давления, действующих на поверхность тела со стороны жидкости, называется выталкивающей силой или силой Архимеда. Истинная причина появления выталкивающей силы — наличие различного гидростатического давления в разных точках жидкости.
Сила Архимеда
ρ ж — плотность жидкости [кг/м 3 ]
V погр — объем погруженной части тела [м 3 ]
g — ускорение свободного падения [м/с 2 ]
На планете Земля: g = 9,8 м/с 2
А теперь давайте порешаем задачки.
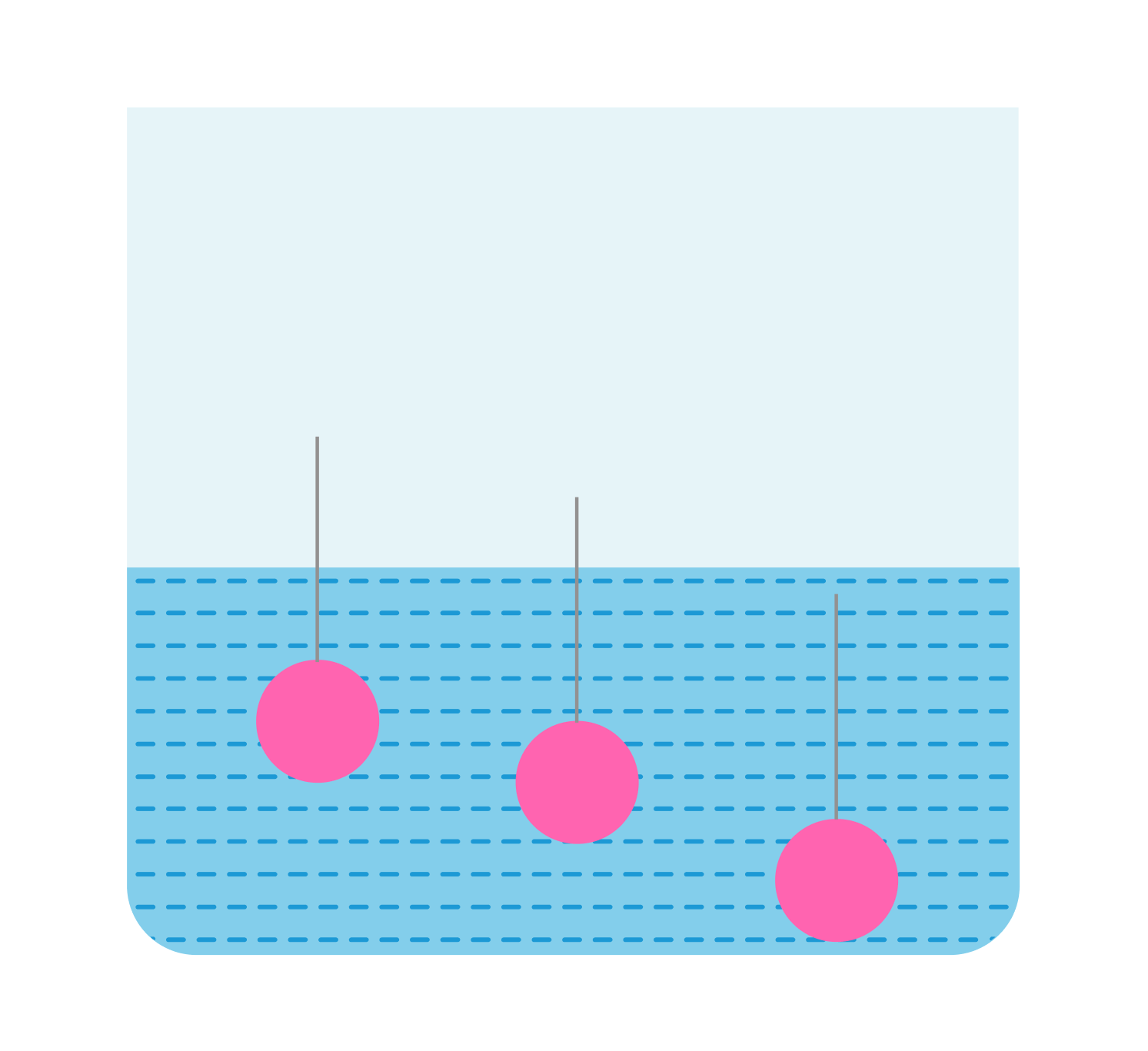
Задача 1
В сосуд погружены три железных шарика равных объемов. Одинаковы ли силы, выталкивающие шарики? (Плотность жидкости вследствие ничтожно малой сжимаемости на любой глубине считать примерно одинаковой).
Решение:
Да, так как объемы одинаковы, а архимедова сила зависит от объема погруженной части тела, а не от глубины.
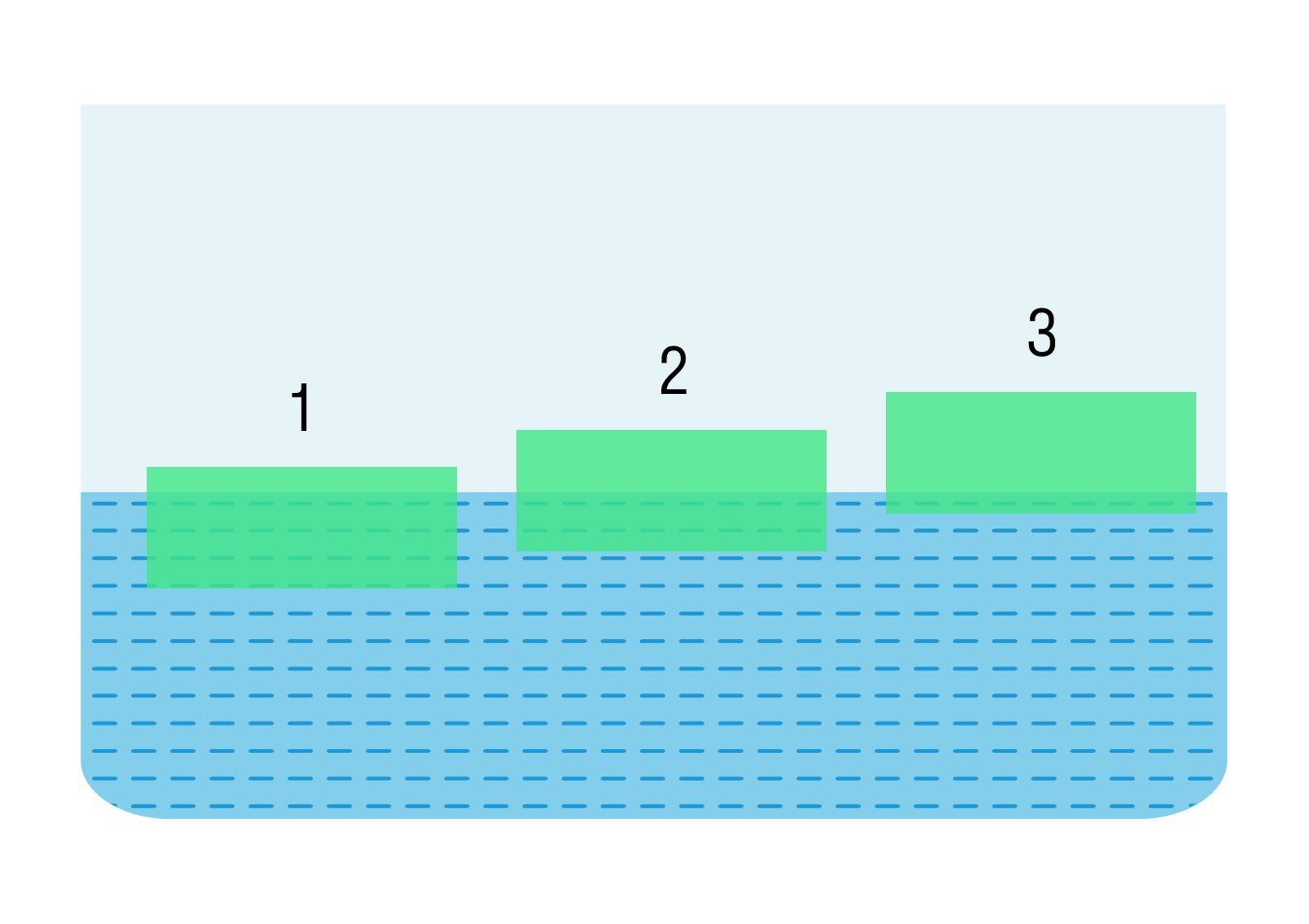
Задача 2
На поверхности воды плавают бруски из дерева, пробки и льда. Укажите, какой брусок из пробки, а какой изо льда? Какая существует зависимость между плотностью тела и объемом этого тела над водой?
Решение:
Чем меньше плотность тела, тем большая часть его находится над водой. Дерево плотнее пробки, а лед плотнее дерева. Значит изо льда — материал №1, а из пробки — №3.
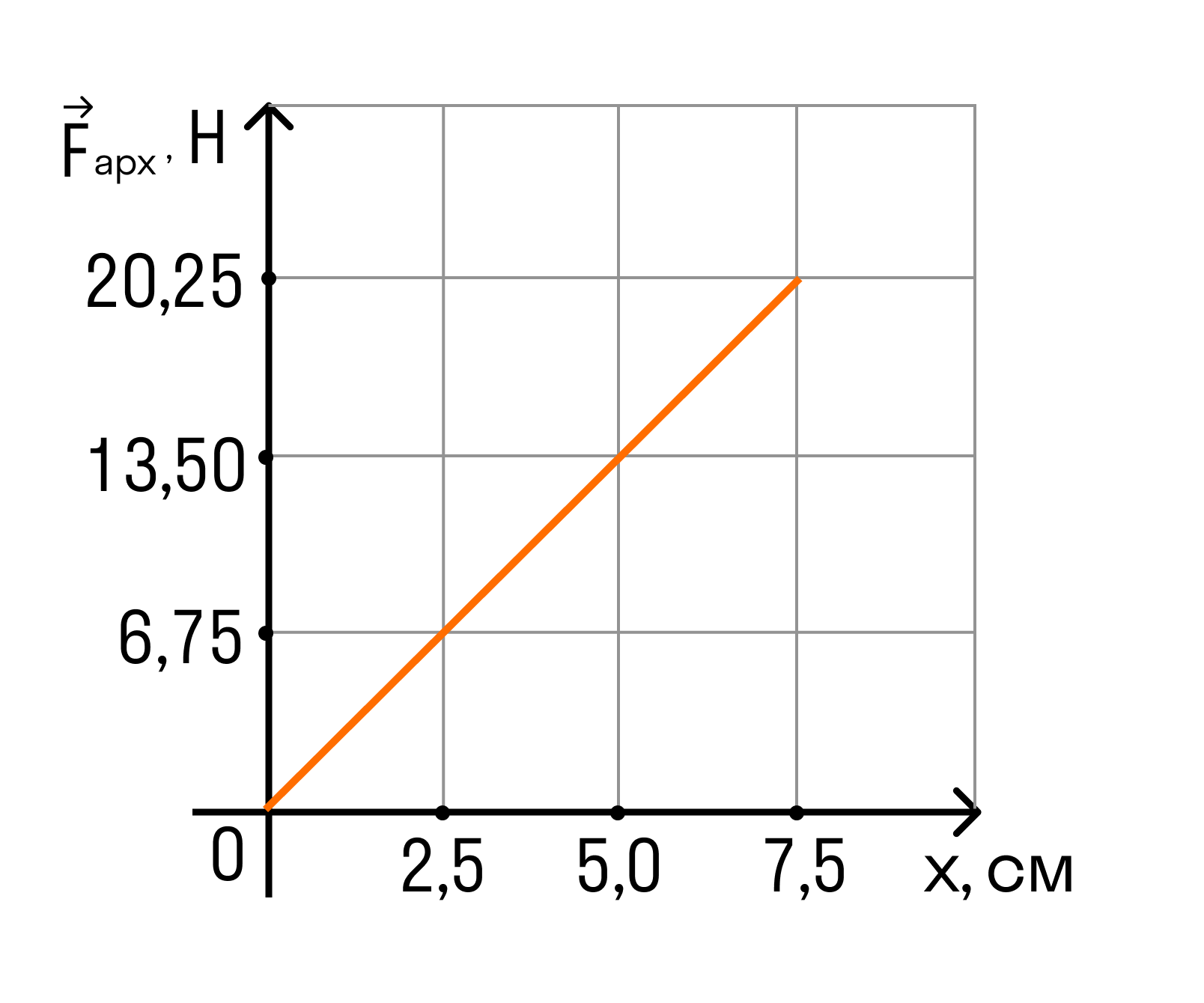
Задача 3
На графике показана зависимость модуля силы Архимеда FАрх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание всё время параллельно поверхности жидкости. Определите плотность жидкости. Ускорение свободного падения принять равным 10 м/с 2 .
Решение:
Сила Архимеда, действующая на кубик равна FАрх = ρж * g * Vпогр
V — объём погруженной части кубика,
ρ — плотность жидкости.
Учитывая, что нижнее основание кубика всё время параллельно поверхности жидкости, можем записать:
а — длина стороны кубика.
ρ = FАрх / (g * a 2 * x)
Рассматривая любую точку данного графика, получим:
ρ = FАрх / (g * a 2 * x) = 20,25 / (10 * 7,5 * 10 -2 ) = 2700 кг/м3
Ответ: плотность жидкости равна 2700 кг/м 3
Задача 4
В сосуде с водой, не касаясь стенок и дна, плавает деревянный кубик с длиной ребра 20 см. Кубик вынимают из воды, заменяют половину его объёма на материал, плотность которого в 6 раз больше плотности древесины, и помещают получившийся составной кубик обратно в сосуд с водой. На сколько увеличится модуль силы Архимеда, действующей на кубик? (Плотность сосны — 400 кг/м 3 .)
Решение:
В первом случае кубик плавает в воде, а это значит, что сила тяжести уравновешивается силой Архимеда:
FАрх1 = mg = ρт * g * a 3 = 400 * 0,2 3 * 10 = 32 Н
После замены части кубика его средняя плотность станет равной
0,5 * 400 + 0,5 * 2400 = 1400 кг/м 3
Получившаяся плотность больше плотности воды = 100 кг/м 3 . Это значит, что во втором случае кубик полностью погрузится в воду. Сила Архимеда в этом случае будет равна:
FАрх2 = ρт * g * Vт = 1000 * 10 * 0,23 = 80 Н
Отсюда получаем, что сила Архимеда увеличится на 48 Н.
Ответ: сила Архимеда увеличится 48 Н
Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.
Плавание тел
Из закона Архимеда есть следствия об условиях плавания тел.
Условия плавания тел
Плавание внутри жидкости
Плавание на поверхности жидкости
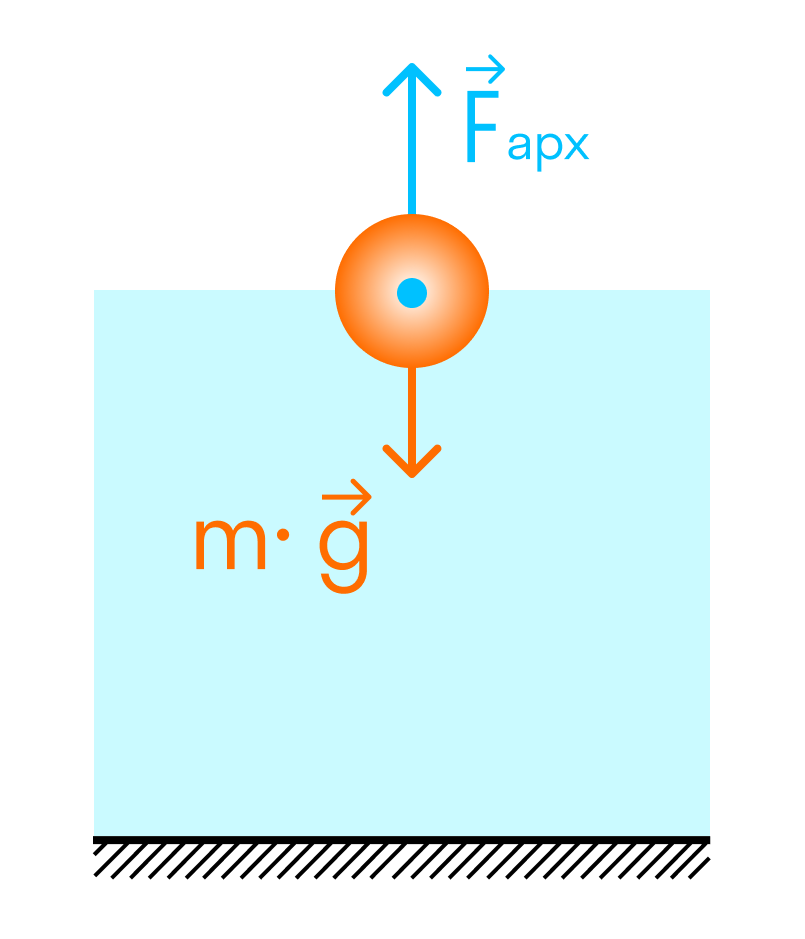
Если плотность тела больше, чем плотность жидкости или газа, — оно уйдёт на дно
Если плотности тела и жидкости или газа равны — тело будет находиться в безразличном равновесии в толще жидкости или газа.
Если плотность тела меньше плотности жидкости или газа — оно будет плавать на поверхности.
Почему корабли не тонут?
Корабль сделан из металла, плотность которого больше плотности воды. И, по идее, он должен тонуть. Но дело в том, что корпус корабля заполнен воздухом, поэтому общая плотность судна оказывается меньше плотности воды, и сила Архимеда выталкивает его на поверхность. Если корабль получит пробоину, то пространство внутри заполнится водой — следовательно, общая плотность корабля увеличится. Судно утонет.
В подводных лодках есть специальные резервуары, заполняемые водой или сжатым воздухом. Если нужно уйти на глубину — водой, если подняться — сжатым воздухом. Рыбы используют такой же принцип в плавательном пузыре — наполняют его воздухом, чтобы подняться наверх.
Человеку, чтобы не утонуть, тоже достаточно набрать в легкие воздух и не двигаться — вода будет выталкивать тело на поверхность. Именно поэтому важно не тратить силы и кислород в легких на панику и борьбу, а расслабиться и позволить физическим законам сделать все за нас.
Источник: skysmart.ru
Сколько времени нужно железному шарику, чтобы добраться до дна?
Подробности вопроса: Сколько времени потребуется железному шарику, массой 100 грамм, брошенному в воду океана над Мариинской впадиной чтобы добраться до её дна??
комментировать
в избранное up —>
Влади мир Apche l [242K]
10 лет назад
Тонуть он будет больше часа, и от массы я думаю время погружения не зависит. Плотность воды практически одинаковая на дне и на поверхности (разница в 4%) вода не может сжиматься до такой плотности которая бы приблизилась к плотности стали.
Двигаться он будет с приблизительной скоростью 10 км. в час.

автор вопроса выбрал этот ответ лучшим
комментировать
в избранное ссылка отблагодарить
Andre i [35.9K]
10 лет назад
Надо было пару месяцев назад дать Джеймсу Кэмерону шарик, он бы бросил и посмотрел сколько времени он будет падать.
Хотя вряд ли он когда-нибудь доберется до дна именно Марианской впадины — слишком многие факторы могут ему помешать: течение рыба его может сожрать и т.п.
в избранное ссылка отблагодарить
Nikolai Sosiura [151K]
Ну а всё же? Можно как то определить? — 10 лет назад
MD Yoda [2.2K]
рыба сожрать:))) +1!
суровая Марианская рыба:) — 10 лет назад
комментировать
Oroti [36.7K]
10 лет назад
ну, тут все просто: на шарик с одной стороны действует сила тяготения (F=mg), заставляя его опускаться вниз, с другой стороны аржимедова сила (F=pgV) р — плотность жидкости. вот и считаем силу, действующую на шарик: F=g*(pV-m). так же существует формула, по которой вычисляется сила: F=mа, отсюда для шарика в жидкости a=g*(pV-m)/m
а потом, зная силу, из этого вычисляем время. движение равноускоренное. v=at, отсюда t=v/a, далее S=v*v/2a, v=корень(S/2a),
подставляем и вычисляем t=числитель:корень(S/(2g*(pV-m)/m))Знаменатель:g*(pV-m)/m.
к сожалению, нет под рукой таблицы плотностей)))) кто-нибудь, подставьте в формулу значения.
Источник: www.bolshoyvopros.ru
Плавучесть

Почему одни вещества тонут в воде, а другие нет? И почему есть так мало веществ, способных плавать в воздухе (т. е. летать, см. статью «Полёт«)? Понимание законов плавучести (и погружения) позволяет инженерам строить корабли из металлов, которые тяжелее воды, и конструировать дирижабли и воздушные шары, способные плавать в воздухе. В спасательный жилет накачивают воздух, поэтому он помогает человеку держаться на воде.
Почему предметы плавают
Если погрузить тело в воду, оно вытеснит некоторое количество воды. Тело занимает место, где раньше была вода, и уровень поды поднимается. Если верить легенде, древнегреческий ученый Архимед (287 — 212 до н.э.), находясь в ванне, догадался, что погруженное тело вытесняет равный объем воды. На средневековой гравюре изображен Архимед, совершивший свое открытие.
Сила, с которой вода выталкивает погруженное и нее тело, называется силой выталкивания. Когда она равна весу тела, тело плавает и не тонет. Тогда вес тела равен весу вытесненной им воды. Пластмассовый утёнок очень лёгкий, поэтому достаточно небольшой силы выталкивания, чтобы удержать его на поверхности. Сила, направленная вниз (вес тела) зависит от плотности тела.
Плотность представляет собой отношение массы тела к его объему. Стальной шар тяжелее яблока того же размера, так как он плотнее. Частицы вещества в шаре упакованы более плотно. Яблоко может плавать в воде, но стальной шар тонет.
Чтобы тело не тонуло, его плотность должна быть меньше плотности воды. В противном случае силы выталкивания воды недостаточно, чтобы удержать тело на поверхности. Относительной плотностью тела называется его плотность по отношению к плотности воды. Относительная плотность воды равна единице, значит, если относительная плотность тела больше 1, оно утонет, а если меньше — будет плавать.
Закон Архимеда
Закон Архимеда гласит, что сила выталкивания равна весу жидкости, вытесненной погруженным в неё телом. Если сила выталкивания меньше веса тела, то оно тонет, если она равна весу тела, оно плавает.
Как плавают корабли
В наши дни корабли делают из стали, которая в 8 раз плотнее воды. Не тонут же корабли потому, что их общая плотность меньше плотности воды. Корабль — это не цельный кусок стали (подробнее о стали в статье «Железо, сталь и прочие металлы«). В нем множества полостей, поэтому его вес распределяется по большому пространству, что и приводит к небольшой общей плотности. «Морской гигант» — одно из самых больших судов мира – весит 564 733 тонны. Благодаря большим размерам выталкивающая сила для него очень велика.
Если хотите увидеть, как действует сила выталкивания, бросьте в сосуд с водой глиняный шарик. Он утонет, и уровень воды поднимется. Отметьте фломастером новый уровень воды. Теперь слепите из этой же глина лодочку и осторожно опустите её на воду. Как видите, вода поднялась ещё выше.
Лодочка вытесняет больше воды, чем шарик, а значит, и сила выталкивания больше.
Грузовые марки
Грузовые марки — это линии, начерченные на борту судна. Они показывают, сколько груза судно может выдержать тех или иных условиях. Так, поскольку холодная вода плотнее теплой, она выталкивает судно сильнее. Значит, судно может взять па борт больше груза. Солёная вода плотнее пресной, следовательно, в пресной воде судно следует меньше нагружать.
Изобрел грузовые марки Сэмюэл Плимсолл (1824-1898). Когда судно погружается в воду до соответствующей линии (см. рис.), оно считается полностью нагруженным. Значение буквенных символов: TF – пресная вода тропики, SF – пресная вода летом, T – солёная вода тропики, S – солёная вода летом, W – солёная вода зимой, WNA – Сев. Атлантика зимой.
Воздухоплавание
Тела могут летать по тем же причинам, по каким они плавают в воде. На них действует сила выталкивания воздуха. Плотность воздуха так мала, что в нем могут плавать очень немногие тела. Это, например, баллоны с горячим воздухом, который менее плотен, чем холодный. Воздушные шары можно также наполнить гелием или другими газами, которые легче воздуха.
Суда и лодки
Когда-то лодки и суда плавали, повинуясь силе ветра или мускульной силе человека. Создание двигателя позволило кораблестроителям использовать винты, толкающие судно сквозь толщу воды. В последнее время появились суда на подводных крыльях. «Великобритания» (построен в 1843 году) – первый железный корабль с гребным винтом. Его приводил в движение паровой двигатель.
Корабль был также оснащён парусами. Контейнеровозы перевозят грузы в больших металлических ящиках. Их можно быстро погрузить на судно и сгрузить обратно при помощи кранов. Одно судно может принять на борт до 2000 контейнеров. Танкеры перевозят нефть и про чие жидкости в баках, расположенных в трюмах.
Некоторые танкеры в 20 раз длиннее теннисного корта.
Подводные лодки
Подводные лодки погружаются и всплывают, изменяя свою относительную плотность. У них на борту есть большие контейнеры – балластные резервуары. Когда из них уходит воздух и внутрь закачивается вода, плотность лодки увеличивается и она погружается. Чтобы всплыть на поверхность, экипаж удаляет из резервуаров воду и накачивает туда воздух.
Плотность вновь уменьшается и лодка всплывает. Балластные резервуары помещаются между внешним корпусом и стенками внутреннего отсека. Экипаж живёт и работает во внутреннем отсеке. Подводная лодка оснащена мощными винтами, которые позволяют ей двигаться сквозь толщу воды. На некоторых лодках установлены атомные реакторы (см. статью «Ядерная энергия и радиоактивность«).
Источник: www.polnaja-jenciklopedija.ru
Архимедова сила | теория по физике гидростатика
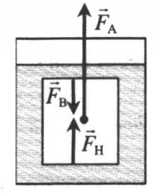
Определение Архимедова сила (выталкивающая сила, подъемная сила)— сила, с которой жидкость или газ выталкивают погруженное в них тело.Полезно знать и понимать!
- Причина возникновения выталкивающей силы: нижняя грань тела находится на большей глубине, чем верхняя, поэтому давление жидкости снизу больше, чем сверху. Из-за разницы в давлениях возникает выталкивающая сила.
- Архимедова сила всегда направлена вертикально вверх.
- Архимедова сила равна разности сил давления на нижнюю и верхнюю грани:
- Также выталкивающая сила равна разности веса тела в воздухе и веса тела в жидкости:
- Модуль выталкивающей силы определяется с помощью закона Архимеда.
Закон Архимеда
Выталкивающая сила равна весу вытесненной жидкости.
Частные случаи определения архимедовой силы
Полное погружение

Архимедова сила равна произведению плотности жидкости, объема тела и ускорения свободного падения:
Vт — объем погруженного в жидкость тела.
Неполное погружение

Архимедова сила равна произведению плотности жидкости, объема погруженной части тела и ускорения свободного падения:
Vп.ч. — объем погруженной в жидкость части тела.
Внимание! Если тело погружено в газ, то в формуле нужно использовать плотность этого газа.
Пример №1. При взвешивании груза в воздухе показание динамометра равно 1 Н. При опускании груза в воду показание динамометра уменьшается до 0,6 Н. Найдите значение выталкивающей силы.
Выталкивающая сила равна разности веса тела в воздухе и веса тело в воде. Следовательно:
Воздухоплавание
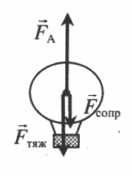
Подъемной силой воздушного шара служит архимедова сила, равная:
Подъемной силе противостоят сила тяжести и сила сопротивления воздуха:
Управление шаром:
- чтобы взлететь, шар заполняют нагретым воздухом или газом, плотность которого меньше плотности окружающего воздуха;
- чтобы увеличить высоту полета, с шара сбрасывают балласт;
- чтобы спуститься на землю, газ охлаждают.
Пример №2. Аэростат объемом 1000 м 3 заполнен гелием. Плотность гелия 0,18 кг/м 3 , плотность воздуха 1,29 кг/м 3 . Какая выталкивающая сила действует на аэростат?
Выталкивающая сила зависит только от плотности окружающей среды и объема погруженного в него тела. Так как аэростат погружен в воздух полностью:
Архимедова сила и законы Ньютона
Если тело полностью погружено в жидкость (или газ):
Частный случай
Определить минимальную массу груза, который следует положить на плоскую однородную льдину площадью S, чтобы она полностью погрузилась в воду. Толщина льдины h, а плотность льда ρл, плотность воды ρв.
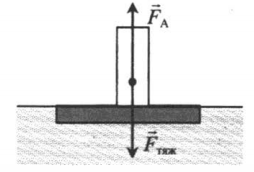
Второй закон Ньютона в векторной форме для льдины, полностью погруженной в воду (она не тонет и не всплывает):
→ F A + → F т я ж = 0
Так как эти силы направлены в противоположные стороны:
Архимедова сила, действующая только на льдину, равна:
Сила тяжести равна сумме масс льдины и груза:
Массу льдины можно выразить через произведение ее плотности на объем, равные произведению ее площади на толщину:
Пример №3. Какую силу надо приложить, чтобы поднять под водой камень, масса которого 30 кг, а объем 12 000 см 3 ?
12 000 куб. см = 0,012 куб. м
Чтобы поднять под водой камень, потребуется сила, равная разности силе тяжести и архимедовой силы, действующей на этот камень:
Условия плавания тел
На любое тело, погруженное в жидкость или газ, действуют две противоположно направленные силы: сила тяжести и архимедова сила. Направление движения тела зависит от того, какая из этих сил больше по модулю:
Внимание! Тело, имеющее плотность меньшую, чем плотность жидкости, в которой оно плавает, будет находиться на поверхности, погрузившись в жидкость частично.
Если тело плавает на поверхности:
- Архимедова сила и сила тяжести, действующие на него, равны: FA= Fтяж.
- Сила тяжести равна: Fтяж = mg = ρтVтg.
- Архимедова сила равна: FA = ρжVп.ч.g.
- Взаимосвязь между объемом и высотой тела правильной формы: V = Sh.
Варианты условий задач на условия плавания тел
Сплошное тело объемом Vт плавает в воде. Причем под водой находится 3/4 его объема. Определите силу тяжести, действующую на тело. Плотность воды ρв.
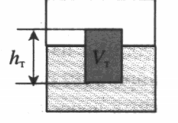
Второй закон Ньютона в векторной форме:
→ F A + → F т я ж = 0
Отсюда (проекция на вертикальную ось):
Какая часть (в процентах) айсберга находится под водой? Плотность льда ρл, а воды ρв.
Второй закон Ньютона в векторной форме:
→ F A + → F т я ж = 0
Отсюда (проекция на вертикальную ось):
Ускорение свободного падения взаимоуничтожается. Чтобы найти погруженную часть айсберга в процентах, нужно:
V п . ч . V л . . = ρ л ρ в . .
Найденное отношение остается умножить на 100%.
Полое тело плотностью ρт плавает в воде, погрузившись на 1/5 своего объема. Найдите объем полости Vп, если объем тела Vт, а плотность воды ρв.
Второй закон Ньютона в векторной форме:
→ F A + → F т я ж = 0
Отсюда (проекция на вертикальную ось):
Преобразовав выражение, получим:
V п = V т ( 5 ρ т − ρ в ) 5 ρ т . .
Пример №4. Кубик массой 40 г и объемом 250 см 3 плавает на поверхности воды. Найдите значение выталкивающей силы, действующей на кубик.
250 см 3 = 250∙10 –6 м 3
Так как тело плавает, Архимедова сила будет равна по модулю силе тяжести, которая определяется формулой:
Деревянный шарик плавает в стакане с водой. Как изменятся сила тяжести и архимедова сила, действующие на шарик, если он будет плавать в подсолнечном масле?
Для каждой величины определите соответствующий характер изменения:
- Увеличится.
- Уменьшиться.
- Не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Записать условие плавания тел.
- На основании условия плавания тел сделать вывод о том, как изменятся указанные физические величины.
Решение
По условию задачи деревянный шарик плавает на поверхности воды. Но это возможно, лишь когда архимедова сила равна силе тяжести:
Если шарик будет плавать в подсолнечном масле, также можно применить условие плавания тел:
Сила тяжести зависит только от массы тела, которая остается неизменной. Поэтому сила тяжести тоже не меняется. Но из этого следует:
Это возможно благодаря тому, что объем погруженной части шарика в масло будет больше объема погруженной части шарика в воду. Этим компенсируется разница в плотностях жидкостей, но архимедова сила при этом остается неизменной.
Верный ответ: 33.
Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В его распоряжении имеется установка, состоящая из ёмкости с водой и сплошного деревянного шарика объёмом 30 см 3 . Какая из следующих установок необходима ещё ученику для того, чтобы на опыте обнаружить зависимость силы Архимеда от объёма тела?
| № установки | Жидкость, налитая в ёмкость | Объём шарика | Материал, из которого сделан шарик |
| 1 | вода | 30 см 3 | сталь |
| 2 | вода | 20 см 3 | дерево |
| 3 | керосин | 20 см 3 | дерево |
| 4 | подсолнечное масло | 30 см 3 | сталь |
Алгоритм решения
- Сделать анализ задачи. Определить, какие величины в опыте остаются постоянными.
- Определить, какие величины должны быть в опыте переменными.
Решение
Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В формулировке слово «жидкость» используется в единственном числе. Следовательно, жидкость во всех опытах будет одной и той же (плотность жидкости будет постоянной). У ученика уже есть установка, в которую входит емкость с водой.
Поэтому во второй установке в качестве жидкости тоже должна использоваться вода. Варианты 3 и 4 исключаются.
В формулировки задачи также говорится о «телах». Они могут быть выполнены из разных материалов, и они могут иметь разный объем. Но известно, что архимедова сила зависит только от объема тела. Поэтому во второй установке нужно использовать тело другого объема. В вариантах 1 и 2 этому условию соответствует деревянный шарик объемом 20 куб. см (так как в первой установке используется шарик объемом 30 куб. см).
Отсюда верный ответ: б.
Необходимо экспериментально изучить зависимость силы Архимеда, действующей на тело, погружённое в жидкость, от плотности жидкости.
Какие две установки следует использовать для проведения такого исследования?
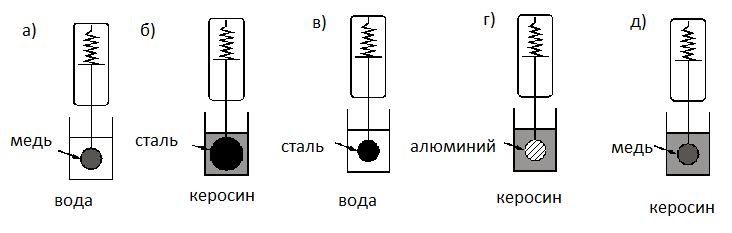
Алгоритм решения
- Установить цели опыта.
- Сделать вывод о том, какие величины в опыте должны быть постоянными, а какие — переменными.
- Выбрать установки, соответствующие выводу.
Решение
В опыте нужно изучить зависимость силы Архимеда, действующей на тело, погружённое в жидкость, от плотности жидкости. Это значит, что плотность жидкости — величина переменная. Все остальные величины при этом должны оставаться постоянным. Поэтому нам нужны установки с разными жидкостями, но одинаковыми телами. Этому условию соответствуют две установки: «а» и «д».
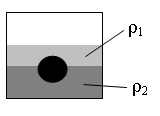
На границе раздела двух несмешивающихся жидкостей, имеющих плотности ρ1 = 400 кг/м 3 и ρ2 = 2ρ1, плавает шарик (см. рисунок). Какой должна быть плотность шарика ρ, чтобы выше границы раздела жидкостей была одна четверть его объёма?
Алгоритм решения
Источник: spadilo.ru
О рыбалке и не только.
Рыбалка — одно из интереснейших увлечений, которое помогает человеку слиться с природой и с пользой провести свое время. В этом блоге Вы найдёте много полезных советов от бывалых рыбаков.
пятница, 1 апреля 2011 г.
Как правильно промерить дно водоема.
Пользовательского поиска
Задача спиннингиста часто заключается в том, чтобы опустить блесну ко дну. Один из способов достижения этого заключается в системе отсчета. Его хорошо использовать при работе с тонущими приманками, такими как колеблющиеся блесны, вращающиеся блесны и тонущие воблеры. Метод также действует и при добавлении грузила на леску в 120—180 сантиметрах от плавающего воблера.
После заброса приманка падает на поверхность воды и начинает погружаться, сматывая леску с катушки, пока не достигнет дна. Когда натяжение лески ослабло, приманка лежит на дне, и пора начинать подмотку. Чтобы определить глубину, начинайте отсчет, как только приманка коснется поверхности воды: 21, 22, 23,— пока леска не провиснет. Затем начинайте подмотку.
При следующем забросе начните подмотку, не досчитав до отмеренного вами числа одну цифру. Идея заключается в том, чтобы отсчитать погружение приманки на нужную глубину. Начав в нужный момент подмотку, вы будете знать, что ваша приманка движется вдоль дна именно на той глубине, где и обитают хищники. Это надежный метод определения мест обитания рыбы и косвенное средство измерения глубины водоема. Если предположить, что приманка тонет со скоростью один метр в секунду, а произнести цифру 21 у вас займет примерно столько же времени, то при счете 27 ваша приманка должна находиться на глубине семи метров.
Нет нужды использовать эту систему отсчета глубины постоянно. Немножко практики, и вы поймете, как быстро тонет приманка, когда следует начать подмотку и на какой глубине стоит рыба. Для спиннингиста это один из важных моментов, так как по провисанию лесы определяется глубина водоёма. Поэтому остановимся на этом явлении подробнее.
Когда леса упадёт на воду, она в первый момент ослабнет, но очень быстро натянется снова, и будет очень хорошо видно, как точка соприкосновения её с водой довольно быстро удалится от спиннингиста. Отойдя на некоторое расстояние, эта точка снова начнёт приближаться к спиннингисту и будет как бы бежать по воде.
В тихую погоду часто можно наблюдать очень интересное и забавное явление: если леса сатурновая, то мелкая рыбёшка — плотички, голавлики и уклейки — пытаются хватать эту бегущую точку, очевидно, принимая её за садящееся на воду насекомое. Я наблюдал несколько раз, как окунишки грамм на 50—60 проделывали эту “ловлю”. Следя за бегом этой точки, вы увидите, как леска вдруг сразу провиснет и ляжет на воду. По удилищу это тоже чувствуется, так как натяжение лесы ощущается. Провисание лесы показывает, что груз сел на дно.
Спиннингисту нужно обязательно уловить момент соприкосновения груза с дном и знать, сколько времени пройдёт от момента падения груза на воду до соприкосновения его с дном водоёма. Узнаётся это путём отсчёта про себя секунд. Если при грузе в 17 г и блесне в 7 г бег точки соприкосновения лесы с водой продолжается в течение 18—20 секунд, то это свидетельствует о глубине около 10 м.
Промер глубин этим способом рекомендуется применять во всех случаях. Тогда вы всегда и в любом месте будете хорошо ориентированы в положении блесны. Особенно это необходимо делать при ловле в коряжистых местах. Глубина расположения коряг должна быть известна; она будет измеряться цифрой вашего отсчёта.
Это позволит вам начать подмотку в тот момент, когда блесна ещё не дойдёт до коряг. Допустим, что коряги расположены на отсчёте 12. Это значит, что если вы начнёте подмотку при счёте 12, то груз заденет за корягу. Для того чтобы блесна не задела корягу, нужно подмотку начинать при счёте 10 или 9.
Само собой разумеется, что для спиннингиста такой способ измерения глубины является по существу единственно доступным. У старых спиннингистов вырабатывается привычка, как только блесна и груз упадут на воду, считать и таким путём определять приблизительную глубину водоёма. На незнакомом водоёме целесообразно сначала привязывать специальный грузик (“глубомер”) и делать несколько забросов специально для определения глубины и характера дна. После этого можно спокойно привязывать рабочий груз и блесну и начинать ловить в уверенности, что блесна не будет засажена.
Делаю такую снасть: Главное условие грузило тяжелее грузоподъёмности поплавка в 2,5 3 раза ( у меня поплавок 25гр а груз 80 гр). Первый заброс, отмечаю дальность, просто защёлкиваю лесу на клипсе. Подтягиваю лесу, пока поплавок не упрётся в грузило, а потом отпускаю леску отмеряя при этом по отметкам на удилище до всплытия поплавка. Это если нужно замерить точную глубину.
Ищу бровку просто подтягивая грузило по дну по 1,5 метра примерно, отмеряю снова. Когда начинается заметное уменьшение глубины, это и есть бровка. Оставляю поплавок как буёк, и вторую удочку, нормально оснащённую кидаю прямо на него и отмечаю дальность (так же при помощи клипсы, заодно стараюсь запомнить силу броска и ориентир для правильного направления).
А проверить дно в месте ловли на наличие растительности ещё проще. Вместо круглого грузила цепляю плоское, грамм на 50, а вместо поплавка тройник. Забрасываю в район ловли, полметра протаскиваю груз с тройником по дну, потом резко дёргаю и быстро подматываю, грузило всплывает, если нет на крючке травы, то даже вылетает из воды как блесна.
Если вы уже рыбачите и знаете какая глубина в вашем месте, то не нужно делать специальную снасть для замера глубины на этом же водоёме в других местах. Просто забрасываете снасть, и считаете секунды после всплеска до того, как кормушка ляжет на дно (видно по кончику удилища)»и раз, и два, и три.» Например где я ловлю, кормушка без корма в 50 грамм тонет 12 секунд, я знаю что там глубина 9 10 метров, теперь в другом месте, если тонет 5 секунд, легко подсчитать: 12:10х5=6 метров. Всё просто, и не занимает много времени, дальность заброса , как уже говорил выше, меняю с помощью клипсы.
Промеры глубин с берега. В том случае, когда река несудоходна или отсутствуют плавсредства, промеры глубин следует производить с берега.
Удочка. К длинному удилищу или же к концу наметки привязывают шнур, размеченный кусочками бечевки или лоскутами материи через каждые 10, 20 или 50 см. На свободном конце шнура подвешивают небольшой груз (рис. 10,а). Глубины нешироких водоемов (до 8—10 м) могут определять два мерщика, идущие с промерными удочками по обоим берегам реки.
Шнур с поплавком. На шнуре через каждые 10 или 20 см делают небольшие петли, к которым может привязываться или подвешиваться на крючке специальный поплавок в виде деревянного бруска таких размеров, чтобы он мог выдержать на плаву небольшой груз, но в то же время груз должен быть достаточным для того, чтобы удержать поплавок при соприкосновении груза с дном реки.
Укрепив поплавок на некотором расстоянии от груза (например на 1,5 м) и держа шнур за его конец, забрасывают груз в реку (рис. 10,6). Если поплавок будет плыть, то глубина в этом месте более 1,5 м при меньшей глубине груз ляжет на дно и поплавок задержится на одном месте. Перемещая поплавок на различные петли, размеченные на шнуре, можно получить представление о глубинах реки на исследуемом ее участке.
Передвижной лот. Если исследователи имеют возможность перемещаться по обоим берегам, то на нешироких реках можно в местах измерения глубин перетянуть через реку промерную веревку. Посредине веревки неподвижно укрепляют небольшое металлическое кольцо и через него пропускают шнур с грузом (промерный лот). На реках шириной до 15—20 м один из концов промерной веревки легко может быть переброшен с берега на берег; на более широких реках (до 50—75 м) целесообразно промерную веревку все время переносить в натянутом над поверхностью воды положении.
Натянув перекинутую через реку веревку и установив кольцо над местом измерения глубины, исследователь, держащий промерный лот за лотлинь, отпускает его до тех пор, пока груз не коснется воды, и замечает в этот момент отсчет по лотлиню, приходящийся против кола, на котором удерживается веревка. После этого лот
40
опускают до соприкосновения груза с дном (о чем можно судить по ослаблению натяжения лотлиня) и делают второй отсчет по лотлиню на линии того же кола. Разность отсчетов покажет глубину в измеряемой точке, а ее расстояние от берега может быть установлено по длине промерной веревки (рис. 10,в).
Наклонный лот. Этот лот представляет собой длинный размеченный шнур (лотлинь) с привязанным к нему грузом. В качестве груза можно рекомендовать небольшой мешочек, сшитый из брезента или частой мешковины, наполняемый на месте работы песком или землей. Вес груза должен быть не менее 2 кг.
Раскачав шнур с грузом в направлении, перпендикулярном к линии берега, груз можно резким рывком забросить на 10—15 м от берега. Применение наклонного лота возможно в двух вариантах.
1. Привязанный к лотлиню груз забрасывается в требуемое место водоема. Лотлинь подбирается и натягивается. В треугольнике ЛВС (рис. 11, а) мы знаем длину лотлиня / (сторона АС) и можем измерить угол а между лотлинем и поверхностью воды; из этих данных вычислим, чему равна глубина (h = BC = l sin ).
Для измерения угла а можно применить угломер простейшей конструкции (рис. 11,6), состоящий из двух линеек длиной по 50 см, вращающихся на шарнире с зажимным винтом. На одной из линеек вбиты два загнутых -гвоздика (крючка), которыми линейка подводится под находящийся в воде лотлинь. Другая линейка отво-
дится к поверхности воды в водоеме. Положение линеек (угол а) закрепляется зажимным винтом, после чего угол между линейками может быть измерен обычным транспортиром.
Искомую глубину водоема h по измеренной длине лотлиня и углу а, образованному лотлинем с поверхностью воды, проще всего получить по номограмме (рис. 11, в). Пример: / = 6,3 м, а=35°. Отложив от точки О по лучу с надписью 35° отрезок, соответствующий величи-
не l в масштабе, принятом для значений глубин, получим на этом луче точку К, расстояние которой от оси ОА, выраженное в том же масштабе, даст искомую глубину h=MK=3,6 м.
2. В описанном выше способе измерение угла а приходится производить на урезе водоема, что бывает не всегда удобно. Измерение угла а можно вынести на высоту 1 м над водой. Для этого на урезе воды устанавливают палку АЕ высотой 1 м (рис. 12, а) и лотлинь подтягивают к верхнему концу палки.
42
Глубину водоема Н = ДС = ВЕ можно найти, решив треугольник ABC, в котором АС — 1, АЕ= м и угол ВАС = а.
Аналогично предыдущему, можно составить расчетную номограмму, пользование которой ясно из рисунка 12, б. Так, например, при /=5,7 м и а = 40° глубина водоема h получается по номограмме, равной NL = 3,6 м.
Определение площади водного сечения реки. Умея измерять глубины в отдельных точках и зная положение последних по ширине реки, нетрудно определить площадь поперечного водного сечения. Часть водного сечения, в которой происходит движение воды, называется живым сечением; остальную его часть, где течение воды незаметно (обычно в прибрежных заводях), принято называть мертвым пространством. При вычислении расходов воды площадь мертвого пространства не учитывается.
Проще всего и точнее всего при определении поперечного сечения реки перетянуть через нее промерную веревку (трос) и через равные по ширине расстояния произвести измерение глубин (примерно в 10—20 точках).
Запись результатов наблюдений при определении площади поперечного сечения рекомендуется вести по следующей форме:
44.
По данным измерений, записанным в журнале (графы 1—3), легко вычертить профиль поперечного сечения реки и вычислить его площадь. Такой чертеж удобно сделать на миллиметровке. Пример построения профиля поперечного сечения реки показан на рисунке 13. Для наглядности чертежа и удобства пользования профилем вертикальный масштаб (для глубин) применяют обычно в 10 раз крупнее горизонтального.
Вычисление площади поперечного сечения заключается в определении площадей отдельных отсеков между соседними промерными вертикалями, представляющих собою трапеции или треугольники (по краям сечения), и последующем суммировании этих частных площадей. Найдя полусуммы соседних глубин и помножив их на соответствующие расстояния между промерными вертикалями, получим частные площади, а просуммировав их, и общую площадь поперечного сечения.
Источник: viktor-romanyuk.blogspot.com