Пропорция 1 к 4 это сколько

Вы можете использовать этот инструмент для получения наиболее упрощенного соотношения или для сравнения двух одинаковых соотношений.

Соотношение

Соотношение в математике — это термин, который используется для сравнения двух или более чисел. Он используется, чтобы указать, насколько велика или мала величина по сравнению с другой. В отношении две величины сравниваются с помощью деления. Здесь делимое называется «антецедентом», а делитель — «консеквентом».

Например, в группе из 30 человек 17 из них предпочитают ходить по утрам, а 13 — ездить на велосипеде. Чтобы представить эту информацию в виде соотношения, запишем его как 17:13. Здесь символ ‘:’ читается как «есть к». Таким образом, отношение людей, предпочитающих ходить пешком, к людям, предпочитающим езду на велосипеде, читается как «17 к 13».

Что такое соотношение?

Соотношение определяется как сравнение двух величин в одних и тех же единицах измерения, которое показывает, сколько одного количества присутствует в другом количестве. Коэффициенты можно разделить на два типа. Одно из них — соотношение части к части, а другое — соотношение части к целому. Соотношение частей к частям показывает, как связаны две различные сущности или группы.

Диаметры труб: 1/4, 3/8, 1/2, 3/4 и т. д. Дюймы и миллиметры

Например, соотношение мальчиков и девочек в классе составляет 12: 15, тогда как соотношение частей к целому обозначает соотношение между определенной группой и целым. Например, из каждых 10 человек 5 любят читать книги. Таким образом, соотношение части к целому составляет 5: 10, что означает, что каждые 5 человек из 10 любят читать книги.

Формула соотношения

Мы используем формулу соотношения при сравнении соотношения между двумя числами или величинами. Общая форма представления соотношения между двумя величинами, скажем, «a» и «b», — это a: b, которое читается как «a равно b». Форма дроби, представляющая это соотношение, — a/b.

Чтобы еще больше упростить соотношение, мы следуем той же процедуре, которую используем для упрощения дроби. a:b = a/b. Давайте разберемся в этом на примере. Пример. В классе из 50 учеников 23 девочки, а остальные мальчики. Найдите соотношение количества мальчиков к количеству девочек.

Общее количество студентов = 50; Количество девушек = 23. Общее количество мальчиков = Общее количество учеников — Общее количество девочек
= 50 — 23
= 27 Таким образом, желаемое соотношение (Количество мальчиков: Количество девочек) равно 27:23.

Расчет коэффициентов

• Шаг 1: Найдите величины обоих сценариев, для которых мы определяем соотношение. В данном случае это 15 и 20.
• Шаг 2: Запишите его в форме дроби a /b. Итак, мы записываем это как 15/20.
• Шаг 3: По возможности еще больше упростите дробь. Упрощенная дробь даст окончательное соотношение. Здесь 15/20 может быть упрощено до 3/4.
• Шаг 4: Поэтому соотношение муки к сахару можно выразить как 3:4.

Используйте бесплатный онлайн-калькулятор коэффициентов, чтобы проверить свои ответы при расчете коэффициентов.

Как упростить соотношения?

Соотношение выражает, сколько требуется одного количества по сравнению с другим количеством. Два термина в соотношении могут быть упрощены и выражены в их низшей форме. Соотношения, выраженные в их наименьших выражениях, легко понять и могут быть упрощены так же, как мы упрощаем дроби. Чтобы упростить соотношение, мы используем следующие шаги.

Давайте разберемся в этом на примере. Например, давайте упростим соотношение 18:10.

• Шаг 1: Запишите заданное соотношение a:b в виде дроби a/b. Записав соотношение в виде дроби, мы получим 18/10.
• Шаг 2: Найдите наибольший общий коэффициент ‘a’ и ‘b’. В этом случае GCF из 10 и 18 равен 2.
• Шаг 3: Разделите числитель и знаменатель дроби на GCF, чтобы получить упрощенную дробь. Здесь, разделив числитель и знаменатель на 2, мы получаем, (18÷2)/(10÷2) = 9/5.
• Шаг 4: Представьте эту дробь в форме соотношения, чтобы получить результат. Таким образом, упрощенное соотношение составляет 9:5.

Используйте бесплатный онлайн-калькулятор коэффициентов упрощения, чтобы проверить свои ответы.

Советы и рекомендации по соотношению:

• В случае, если оба числа «a» и «b» равны в соотношении a: b, то a: b = 1.
• Если a > b в соотношении a : b, то a : b > 1.
• Если a < b в соотношении a : b, то a : b < 1.
• Перед их сравнением необходимо убедиться в том, что единицы измерения двух величин одинаковы.

Эквивалентные Соотношения

Эквивалентные соотношения аналогичны эквивалентным дробям. Если предшествующий (первый член) и последующий (второй член) данного соотношения умножаются или делятся на одно и то же число, отличное от нуля, это дает эквивалентное соотношение.

Например, когда антецедент и следствие соотношения 1:3 умножаются на 3, мы получаем, (1 × 3) : (3 × 3) или 3: 9. Здесь 1:3 и 3:9 являются эквивалентными соотношениями. Аналогично, когда оба члена соотношения 20:10 делятся на 10, это дает 2:1. Здесь 20:10 и 2:1 являются эквивалентными соотношениями. Бесконечное число эквивалентных соотношений любого заданного соотношения может быть найдено путем умножения предшествующего и последующего на положительное целое число.

Таблица коэффициентов

Таблица коэффициентов — это список, содержащий эквивалентные коэффициенты любого заданного соотношения в структурированном виде. В следующей таблице соотношений приведено соотношение между соотношением 1:4 и четырьмя его эквивалентными соотношениями. Эквивалентные соотношения связаны друг с другом умножением числа. Эквивалентные соотношения получаются путем умножения или деления двух членов соотношения на одно и то же число. В примере, показанном на рисунке, давайте возьмем соотношение 1:4 и найдем четыре эквивалентных соотношения, умножив оба члена соотношения на 2, 3, 6 и 9. В результате мы получаем 2:8, 3:12, 6:24, и 9:36.

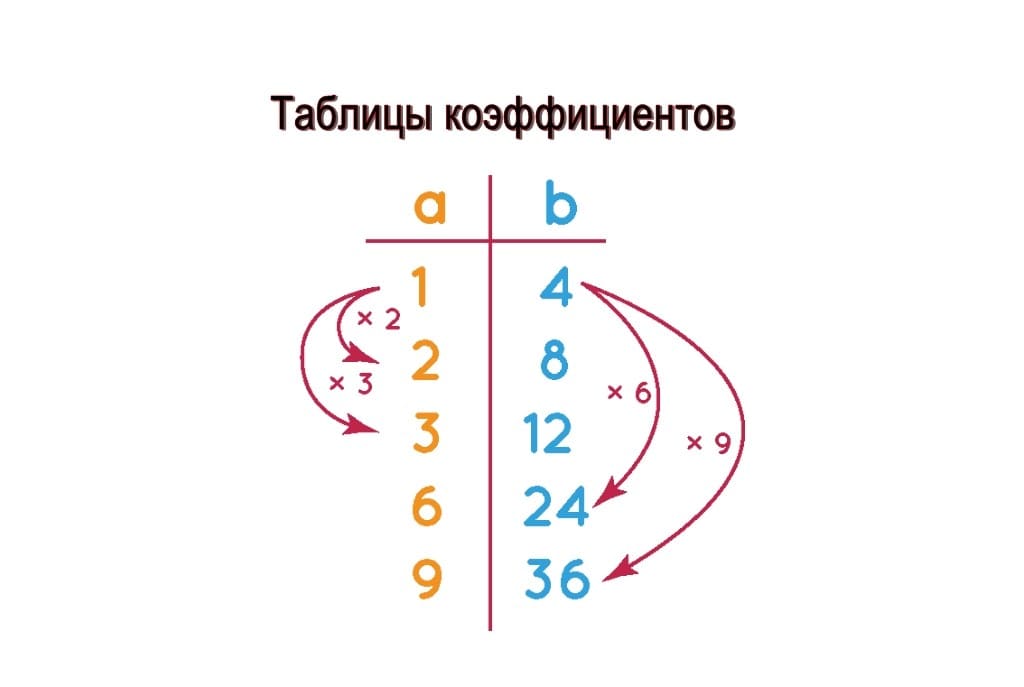
Используйте бесплатный онлайн-калькулятор эквивалентных коэффициентов, чтобы проверить свои ответы.

Примеры соотношения

1. Пример 1. В школьном зале 49 мальчиков и 28 девочек. Выразите соотношение числа мальчиков к числу девочек. Решение: Учитывая, что количество мальчиков = 49, а количество девочек = 28. GCF 49 и 28 равен 7. Теперь, для упрощения, разделите два термина на их GCF, который равен 7. Это означает, (49 ÷ 7)/(28 ÷ 7) = 7/4. Следовательно, соотношение числа мальчиков к числу девочек = 7:4.
2. Пример 2: В музыкальном классе 30 учеников. 10 из них были взрослыми, а остальные — детьми. Каково соотношение числа детей к общему числу учащихся в музыкальном классе? Решение: Учитывая, что общее количество учащихся в музыкальном классе = 30, а общее количество взрослых = 10. Следовательно, количество детей, посещавших музыкальный класс = 30 -10, что равно 20. Отношение общего числа детей к общему числу учащихся в музыкальном классе = 20: 30, что в упрощенном виде дает 2:3.
3. Пример 3: Упростите заданное соотношение, 87:75. Решение: Чтобы упростить данное соотношение, мы сначала найдем GCF 87 и 75, что равно 3. Затем мы разделим каждый член на 3. Это означает, (87 ÷ 3)/(75 ÷ 3) = 29/25. Таким образом, соотношение 87:75 в простейшей форме равно 29:25.

Как ваш ребенок может овладеть математическими понятиями?
Математическое мастерство приходит с практикой и пониманием того, «Почему» стоит за «Что». Почувствуйте разницу в математике.

Источник: www.sas.com.ru

Пропорция 1 к 4 это сколько

Follow Us:

ADVERTISEMENT

Send Us Your Feedback / Suggestion

SEND FEEDBACK

For further assistance, please Contact Us

Обнаружен блокировщик рекламы

Ой! Похоже, вы используете Adblocker!

Поскольку мы изо всех сил пытались сделать для вас онлайн-расчеты, мы обращаемся к вам с просьбой предоставить нам разрешение, отключив Adblocker для этого домена.

Or

Disable your Adblocker and refresh your web page

ADVERTISEMENT
Получить Виджет!

ДОБАВИТЬ ЭТОТ КАЛЬКУЛЯТОР НА ВАШ ВЕБ-САЙТ:

Добавьте калькулятор соотношений на свой сайт, чтобы упростить использование этого калькулятора напрямую. Создайте учетную запись для этого виджета без проблем, поскольку он на 100% бесплатный, простой в использовании и вы можете добавить его на несколько онлайн-платформ.

Имеется в наличии в приложении

Загрузите приложение «Калькулятор коэффициентов» для мобильного телефона, чтобы вы могли рассчитать свои значения в своих руках.

Онлайн-калькулятор соотношений поможет вам определить одинаковые коэффициенты, указав три из четырех частей двух соотношений. Кроме того, этот калькулятор соотношений лучше всего подходит для нахождения пятой и шестой частей из трех соотношений, давая любые четыре части. Наш решатель соотношений выполняет следующие семь операций как с двумя, так и с тремя отношениями.

• Найдите эквивалент отношения
• Сделайте соотношение больше
• Сделайте соотношение меньше
• Упростить соотношение
• Упростите соотношение до формы “1: n: m”
• Упростите соотношение до формы “n: 1: m”
• Упростите соотношение до формы “n: m: 1”

Прежде чем мы собираемся использовать этот калькулятор соотношений, мы должны знать основное определение, формулу соотношения и то, как найти соотношение вручную. Продолжайте читать, чтобы получить краткие сведения о том, как делать соотношения.

Кроме того, вы можете попробовать наш онлайн-калькулятор пропорций, который поможет вам легко решить проблему пропорций разными методами.

Что такое коэффициент?

Его можно определить как «сравнение двух конкретных чисел, очень часто представленных в виде дробей». Просто он показывает, сколько одной части отношения содержится в другой части. Наш искатель соотношений разработан для вычисления этого контраста и определения взаимосвязи между числами.

как посчитать соотношение чисел (шаг за шагом):

Отношение состоит из двух частей: числитель и знаменатель, как и дробь. Если у нас есть два отношения, и мы хотим вычислить соотношение для недостающего значения в соотношении, просто выполните следующие действия:

• Запишите отношения в виде дроби и вставьте любую переменную (x или y) в пропущенное значение
• Установите дроби равными друг другу
• Используя перекрестное умножение, сгенерируйте уравнение
• Найдите недостающую переменную
• Наконец, попробуйте калькулятор соотношений, чтобы проверить свой ответ.

Вы можете воспользоваться нашим онлайн-калькулятором дробей, чтобы сложить, вычесть, умножить или разделить две или три дроби. Здесь у нас есть ручной пример, чтобы прояснить понимание:

Пример:

У нас есть 6 кусочков пиццы, из которых съедаются 2. Теперь мы хотим знать, сколько кусочков можно съесть из 54 кусочков пиццы?

Решение:

Шаг 1:

Запишите соотношение в виде дроби как:

Съеденный ломтик / всего ломтик = 2/6

Съеденный ломтик / всего ломтик = x / 54

Шаг 2:

Приравняйте дроби друг к другу:

Шаг 3:

Мы рекомендуем вам использовать наш калькулятор соотношений, если вы собираетесь решать комплексные отношения больших чисел.

Как использовать онлайн-калькулятор соотношений:

Наш калькулятор – точный инструмент для упрощения и поиска неизвестного значения в соотношении. Вам просто нужно придерживаться следующих пунктов для расчета соотношений:

Входы:

• Прежде всего, нажмите вкладку, чтобы выбрать, сколько соотношений вы хотите выполнить
• вычисления. Это может быть A: B или A: B: C
• Затем выберите метод расчета из раскрывающегося списка этого калькулятора.
• Затем введите в поля в соответствии с выбранными входными параметрами.
• Как только вы закончите, нажмите кнопку расчета

Выходы:

• Отсутствующие значения
• Упрощение соотношения
• Визуальное представление отношения (круговая диаграмма)

Заметка:

Этот калькулятор соотношений не даст вам значений, которые вам не нужны; он даст вам результат в соответствии с входными параметрами.

Что такое золотое сечение?

Когда две величины имеют то же отношение, что и отношение их суммы к большей из двух величин, то это соотношение называется золотым сечением. Например, если величины выражены в x и y, то золотое сечение между x и y равно (x + y) / x = x / y.

Конечное примечание:

К счастью, вы узнали о том, как рассчитать соотношение соотношения вручную и с помощью калькулятора. Соотношение используется везде, от приготовления пищи до строительства дома. Это очень полезно для образования K-12 и во многих других областях науки, таких как механика, бизнес и бухгалтеры, еда и многие другие. Когда дело доходит до решения отношений для комплексных чисел, просто используйте онлайн-калькулятор соотношений, который поможет вам найти недостающее значение в соотношении и выполнить упрощение отношения по вашему желанию.

Источник: calculator-online.net

соотношение 1 4 это сколько

Ответ от Заира Аминтазаева[активный]
Одна ложка димексида на 4 ложки воды. И будьте осторожны, димексид очень согревающее средство, сначала проверьте на аллергию, может нужно разбавлять на большее количество воды

Ответ от ЛЕДИ.. .[гуру]
удобно так- в шприц набираешь 1 кубик лекарства и 4 кубика воды . и используешь. его нельзя оставлять на долго.

Ответ от Ёветлана Бахаева[новичек]
Добрый день, подскажите пожалуйста 1:4 димексида. разводить чайными ложками или столовой.

Ответ от Miss[новичек]
чайными ложками разводить, мне вот щас назначили (1:3 )
Ответ от 22 ответа[гуру]

Привет! Вот подборка тем с похожими вопросами и ответами на Ваш вопрос: Как понять (соотношение 1 : 4) 1 часть р-ра Димексида и 4 часть воды? Это для наружного компресса.

Источник: 22oa.ru

Понимание соотношения сторон в фотографии

Давайте подробно рассмотрим соотношения сторон фото вместе с профессиональным фотографом Назимом Мансуровым и выясним, что нужно знать каждому обо всем этом. Что такое соотношение сторон? В фотографии соотношение сторон представляет из себя соотношение между шириной и высотой изображения. 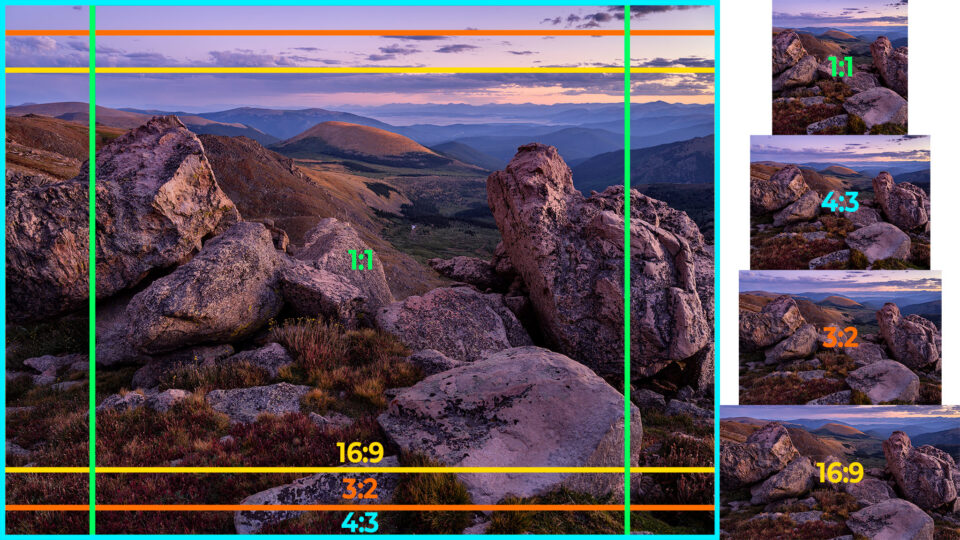Соотношение сторон часто определяется форм-фактором датчика пленки/изображения камеры, который практически всегда является прямоугольным. Наиболее распространенные пропорции современных сенсоров цифровых камер — 3:2 и 4:3. Все современные полнокадровые и зеркальные фотокамеры APS-C имеют сенсоры с соотношением сторон 3:2, тогда как 4:3 — популярный выбор среди смартфонов, Micro Four Thirds и некоторых производителей камер среднего формата.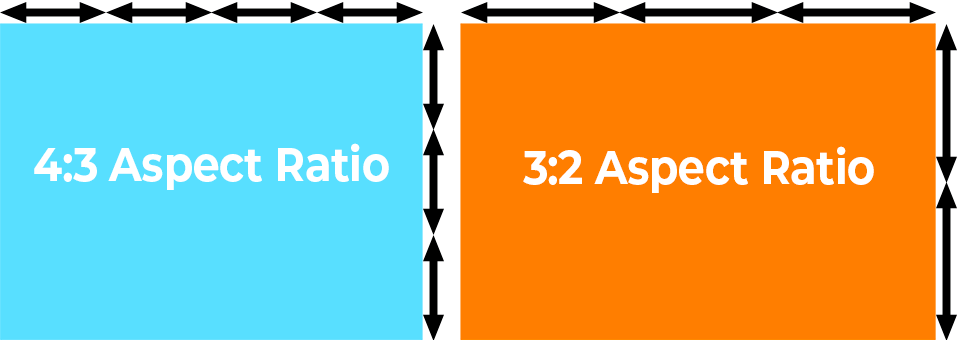

Некоторые камеры позволяют выбирать различные соотношения сторон в меню камеры, предоставляя опции обрезки, отличные от оригинального датчика изображения. Когда соотношение сторон выражается двумя числами, разделенными двоеточием, первое число обычно относится к горизонтальной стороне изображения, а второе число — к вертикальной. Например, 3:2 обозначает горизонтальное изображение, полученное в альбомной ориентации. А 2:3 будет считаться вертикальным изображением, полученным в портретной. Когда соотношение сторон выражается в десятичных числах, таких как 1,50 или 1,50:1, оно игнорирует ориентацию изображения. Почему соотношение сторон важно
Понимание основ соотношения сторон очень важно, потому что это влияет на окончательное изображение. Это может быть особенно важно во время физического захвата фотографии. Например, если вы снимаете изображение с помощью камеры с его собственным соотношением сторон 4:3 и втискиваете свой объект или важные элементы сцены в края кадра, вы не сможете обрезать изображение с более широкими пропорциями. Посмотрите на следующее изображение. Как вы можете видеть, изображение было получено в 4:3, и фотограф едва смог втиснуть здание, а также структуру переднего плана в кадр. Хотя в конце этого конкретного снимка это сработало, просто нет возможности обрезать изображение, чтобы оно соответствовало любым другим форматным соотношениям, без обрезания в здание или элемент переднего плана. То же самое касается выбора чрезвычайно широких форматов изображения, когда камера обрезает верх и низ кадра, как на фото ниже: Когда Назим использовал беспилотник DJI Mavic Pro в Каппадокии, Турция, он забыл, что настроил камеру для съемки изображений в формате 16:9, поэтому получил кучу широких изображений, подобных фото, которое вы видите выше. К сожалению, поскольку верхняя и нижняя части изображения были обрезаны (даже при съемке в формате RAW), пришлось немного обрезать края изображения, чтобы получить 3:2 или 4:3. Посмотрите на то, что изменение этих пропорций сделает с изображением выше. Как вы видите 4:3 — определенно неудачный вариант, поскольку он врезается в элементы переднего плана. Если бы фотограф запечатлел это изображение в его нативном формате 4:3 для начала, он мог бы избежать этой проблемы. Вот почему очень важно обращать внимание на пропорции при составлении композиции и кадрировании снимков — всегда обеспечивайте достаточное «пространство для дыхания» вокруг объекта съемки, если ваша конечная цель состоит в том, чтобы позже было больше вариантов кадрирования. Нативное соотношение против выбора в камере Соотношение сторон часто определяется датчиком изображения камеры, которое является «родным» для нее. Однако некоторые камеры предоставляют фотографам возможность выбирать разные пропорции. Например, Nikon Z7 позволяет выбирать между следующим:

• FX (36×24)
• DX (24×16)
• 5:4 (30×24)
• 1:1 (24×24)
• 16:9 (36×20)

Обратите внимание, что первые два параметра имеют формат 3:2 (FX 36×24 и DX 24×16), поскольку это нативное соотношение сторон сенсора на этой камере (второй вариант предназначен для обрезки центральной части изображения для моделирования датчиков камеры Nikon APS-C/DX). Все остальные параметры, такие как 5:4, 1:1 и 16:9, не являются встроенными, что означает, что выбор любого из них приведет к обрезке части изображения.

Хотя это уменьшает разрешение изображения и размер файла, часто не стоит переключаться на невстроенные пропорции. Прежде всего, вы выбрасываете пиксели, которые никогда не сможете вернуть. Если вы обрежете изображение и решите вернуться и изменить его на другое соотношение сторон, вам придется либо повторно сделать снимок, либо потенциально потерять разрешение из-за дополнительного кадрирования. Если вы снимаете в исходном соотношении сторон, у вас будет возможность изменить его на этапе последующей обработки с минимальной потерей разрешения.

Почему кто-то может захотеть изменить исходное соотношение сторон? Первая причина связана с кадрированием — если вы хотите предотвратить случайную обрезку объекта, то может быть полезно переключиться на соотношение сторон, которое вы будете использовать для отображения или печати изображения. Вторая причина связана с буфером камеры и скоростью непрерывной съемки — некоторые камеры могут снимать дольше из-за хранения меньших файлов в буфере.

Если вы хотите максимизировать разрешение изображений, всегда снимайте в исходном соотношении сторон датчика камеры. Однако если у вас есть особые требования (например, ваш клиент просит, чтобы вы производили изображения с определенным соотношением сторон), то кадрирование в камере будет более безопасным вариантом с точки зрения композиции.

Наиболее распространенные пропорции

Ниже приведены наиболее распространенные пропорции

• 1:1 (1,00) — Некоторые пленочные камеры среднего формата предлагают соотношение сторон 1:1. Тем не менее, ни одна из современных цифровых камер не имеет квадратных датчиков, и только некоторые камеры предлагают 1:1 в качестве опции в меню. Instagram сделал популярным 1:1, изначально применяя его к каждой фотографии, но платформа была изменена для соответствия различным форматам изображения. 1:1 является относительно распространенным для печати квадратных изображений.
• 5:4 (1,25). Соотношение сторон 5:4 довольно распространено в пленочных камерах большого и среднего формата, а также при печати изображений размером 8 ″ x10 ″ и 16 ″ x20 ″.
• 3:2 (1,50). Большинство зеркальных, беззеркальных и компактных камер имеют сенсоры 3:2, независимо от их размера. Соотношение сторон 3:2 было популяризировано 35-мм пленкой, и сегодня оно является наиболее распространенным в фотографии.
• 4:3 (1,33) — средний формат, Micro Four Thirds, большинство смартфонов и некоторые камеры типа «наведи и снимай» имеют сенсоры 4:3.
• 16:9 (1,78) — самый распространенный формат видео сегодня. Не распространенный формат в фотографии, но некоторые камеры предоставляют его в качестве опции кадрирования.
• 3:1 (3,0) — обычно используется для панорамных снимков.

Видеоканал Фотогора

Обсуждение

Вы можете оставить свой комментарий к данной статье

Источник: fotogora.ru