Начальная скорость какая буква

Мир полон движения. Мы часто говорим, что прошли какое-то количество километров, оплачиваем штрафы за превышение скорости и выбираем самый быстрый маршрут в навигаторе. Давайте учиться его характеризовать.

· Обновлено 28 октября 2022

Механическое движение

Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.

Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.

«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:

• тело отсчета
• система координат
• часы

В совокупности эти три параметра образуют систему отсчета.

В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

4 класс. Математика. Скорость, время, расстояние

Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

• Время — в международной системе единиц СИ измеряется в секундах [с].
• Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].

Векторные величины (определяются значением и направлением)

• Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
• Перемещение — вектор, проведенный из начальной точки пути в конечную [м].

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

УЧИМСЯ ЛЕГКО РЕШАТЬ ЗАДАЧИ НА ДВИЖЕНИЕ / ПОДСКАЗКА ВСЕГДА ПОД РУКОЙ СКОРОСТЬ ВРЕМЯ РАССТОЯНИЕ

Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.

Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость

— скорость [м/с]
— перемещение [м]
— время [с]

Средняя путевая скорость

V ср.путевая = S/t

V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]

В чем разница между перемещением и путем?

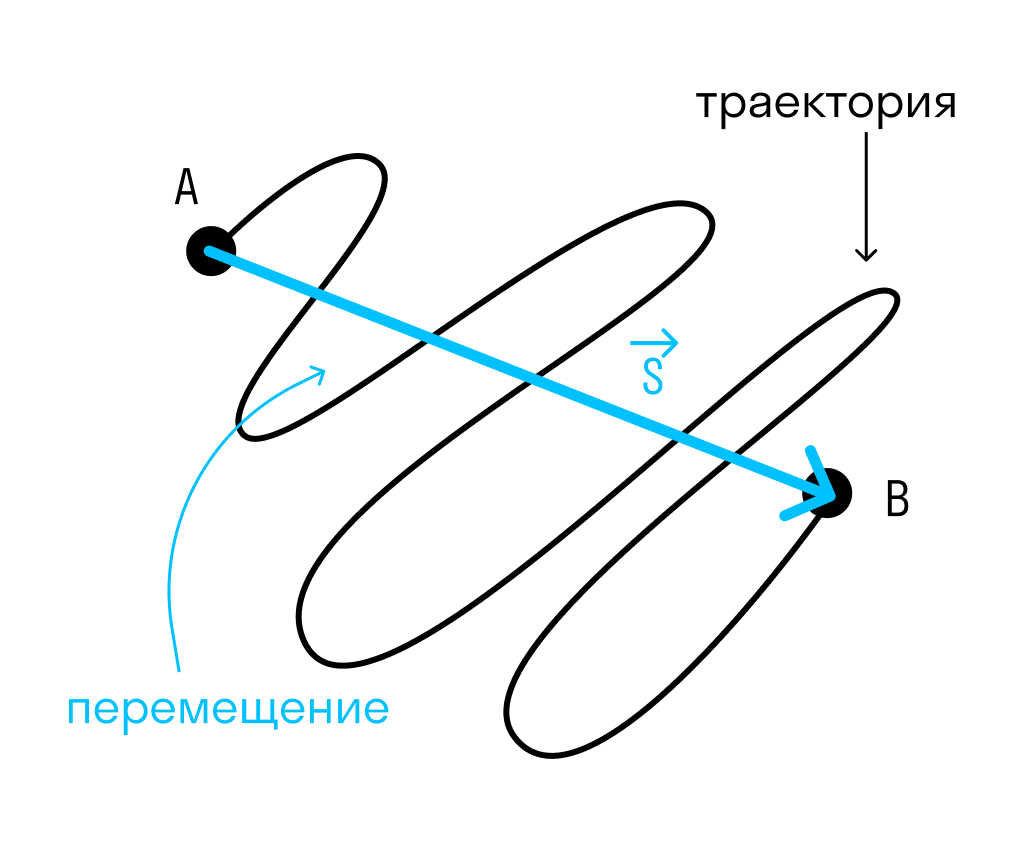
Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости
V ср.путевая = S/t

Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!

Уравнение движения

Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения

x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

Уравнение движения при движении против оси

x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Записаться на интенсив

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».

Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения

x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
v0x — начальная скорость тела в [м/с]
t — время [с]
ax — ускорение [м/с 2 ]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:

Формула конечной скорости

— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с 2 ]

Задача

Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

Так как автобус двигался с места, . Значит

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч 2
Теперь возьмем уравнение движения.
x(t) = x0 + v0xt + axt 2 /2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
км

Ответ: через полчаса координата автобуса будет равна 150 км.

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .

И кому же верить?

Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с 2 .

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Источник: skysmart.ru

Виды скорости в физике и методы их вычисления

Скорость — векторная физическая величина, которая характеризуется направлением и быстротой перемещения материальной точки.

В международной системе единиц (СИ) единица измерения скорости обозначается как метр в секунду ( м с ) . На практике зачастую используют внесистемные единицы измерения скорости. Например: километр в час ( к м ч ) .

В физике понятие скорости встречается в разделе «Кинематика», в котором дается описание механического движения, а это основа изучения скорости как векторной физической величины.

Скорость может характеризоваться быстротой перемещения не только материальной точки, но и еще элементарных частиц и волн. Скорость звука — это величина, которая показывает, на какое расстояние может распространиться звуковая волна за единицу времени. Скорость света — абсолютная величина, которая показывает скорость распространения электромагнитных волн.

Виды скорости в физике, основные характеристики

1. Начальная скорость — это скорость в течении начального момента времени. Начальная скорость подразумевается какой-то момент времени, в который начинается измерение скорости (обычно t = t 0 ).
2. Равномерная скорость — это скорость при равномерном движении, численно равная отношению пути, пройденного телом, ко времени, затраченному на прохождение этого пути.
3. Средняя скорость — это отношение всего пройденного пути к затраченному на это движение времени.
4. Мгновенная скорость — это векторная величина, равная отношению перемещения к малому промежутку времени, за которое это перемещение производится.

Скорость принято записывать буквой ϑ , в СИ она обозначается как м с .

Как писалось выше, скорость равна отношению пути S ко времени t.

Формулы скорости при движении разных видов

Нахождение начальной скорости зависит от задачи и от исходных данных. Ее можно найти по конечной скорости, ускорению и времени: ϑ н = ϑ 0 — ( α ∙ t ) , где:

ϑ н — начальная скорость;

ϑ 0 — конечная скорость;

Равномерная — находится по обычной формуле скорости: ϑ = S t , где:

Формула средней скорости: ϑ с р = S о б щ t о б щ .

Формула мгновенной скорости: ϑ ⇀ = ∆ S ⇀ ∆ t .

Примеры задач с решением

На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?

Решение:

Скорость — это расстояние, пройденное телом за единицу времени. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения.

Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это и есть скорость движения.

ϑ = 180 3 = 60 к м ч

Ответ: скорость автомобиля составляет 60 км/ч.

Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа — со скоростью 90 км/ч, а затем два часа — со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

В условии сказано о трех участках пути.

ϑ с р = S о б щ t о б щ

ϑ с р = S 1 + S 2 + S 3 t 1 + t 2 + t 3

Участки пути нам не даны, но мы можем без труда их вычислить:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

ϑ с р = 100 + 180 + 160 1 + 2 + 2 / = 440 5 = 88 к м ч

Ответ: средняя скорость составляет 88 км/ч.

Конечная скорость после 2 секунд движения с ускорением 0,2 м/с², равна 3 м/с. Найти начальную скорость.

ϑ н = ϑ 0 — ( α ∙ t )

ϑ н = 3 — ( 0 , 2 ∙ 2 ) = 2 , 6 м с

Ответ: начальная скорость составляет 2,6 м/с.

Источник: wika.tutoronline.ru

Формулы кинематики с пояснениями по физике

Кинематика — раздел физики, занимающийся исследованием законов движения идеальных тел.

Основные формулы с пояснениями, которые помогут в решении заданий ЕГЭ по физике: движение, скорость, ускорение.

Путь, время, скорость

• S — путь
• v — скорость
• t — время

Равномерное движение

• x — координата
• x0 — начальная координата
• v — скорость
• t — время

Равномерно ускоренное движение: ускорение

• a — ускорение
• v — скорость
• v0 — начальная скорость
• t — время

Равномерно ускоренное движение: скорость

• v — скорость
• v0 — начальная скорость
• a — ускорение
• t — время

Равномерно ускоренное движение: путь

• s — путь
• v — скорость
• t — время
• a — ускорение

Равномерно ускоренное движение: координата

• x — координата
• x0 — начальная координата
• v — скорость
• t — время
• a — ускорение

Высота тела, брошенного вертикально вверх (вниз)

h=h_0 + v_ < 0 >t — frac < gt^2 >

• h — высота
• h0 — начальная высота
• v0 — начальная скорость
• t — время
• g — ускорение свободного падения

Скорость тела, брошенного вертикально вверх (вниз)

• v — скорость
• v0 — начальная скорость
• g — ускорение свободного падения
• t — время

Скорость, ускорение, время

• v — скорость
• a — ускорение
• t — время

Скорость свободно падающего тела

• v — скорость
• g — ускорение свободного падения
• t — время

Центростремительное ускорение

• a — центростремительное ускорение
• v — скорость
• R — радиус

Угловая скорость

• ω — угловая скорость
• φ — угол
• t — время

Равномерное круговое движение

• l — длина дуги окружности
• R — радиус
• φ — угол

Равномерное круговое движение: линейная скорость

• v — линейная скорость
• R — радиус
• ω — угловая скорость

Период вращения

• T — период
• t — время
• N — число вращений

• T — период
• R — радиус
• v — линейная скорость

• T — период
• ω — угловая скорость

Центростремительное ускорение

• a — центростремительное ускорение
• R — радиус
• T — период вращения

• a — центростремительное ускорение
• R — радиус
• n — частота вращения

Частота вращения

• n — частота вращения
• T — период вращения

Центростремительное ускорение

• a — центростремительное ускорение
• ω — угловая скорость
• R — радиус

Дальность броска тела, брошенного под углом к горизонту

• x — координата (дальность)
• v0 — начальная скорость
• t — время
• α — угол

Высота подъема тела, брошенного под углом к горизонту

y=v_0t sin (alpha) — frac < gt^2 >

• y — координата (высота подъема )
• v0 — начальная скорость
• t — время
• g — ускорение свободного падения
• α — угол

Вертикальная скорость тела, брошенного под углом к горизонту

v_y=v_0* sin (alpha) — gt

• vy — вертикальная скорость
• v0 — начальная скорость
• α — угол
• g — ускорение свободного падения
• t — время

Максимальная высота подъема тела, брошенного под углом к горизонту

• hмакс — максимальная высота
• v0 — начальная скорость
• α — угол
• g — ускорение свободного падения

Общее время движения тела, брошенного под углом к горизонту

• t — время
• v0 — начальная скорость
• α — угол
• g — ускорение свободного падения

Дальность броска тела, брошенного горизонтально

• x — координата (дальность)
• x0 — начальная координата
• v — скорость
• t — время

Высота подъема тела, брошенного горизонтально

• y — координата (высота подъема)
• y0 — начальная координата (высота)
• g — ускорение свободного падения
• t — время

Общее время движения тела, брошенного горизонтально

• tмакс — максимальное время
• h — высота
• g — ускорение свободного падения

Смотри также:

• Формулы МКТ
• Справочные материалы по физике
• Физические величины и единицы их измерения

Источник: bingoschool.ru

Механическое движение и его характеристики

Определения Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними. Основная задача механики — определение положение тела в пространстве в любой момент времени. Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение и его виды

• Поступательное. Это движение, при котором все точки тела движутся одинаково. Если через тело мысленно провести прямую, то после изменения положения этого тела в пространстве данная прямая останется параллельной самой себе.
• Вращательное. Это движение, при котором все точки тела движутся, описывая окружности.
• Колебательное. Это движение тела, которое повторяется точно или приблизительно через определенные интервалы времени. От вращательного движения его отличает то, что при колебаниях тело перемещается в двух взаимно противоположных направлениях.

По типу линии, вдоль которой движется тело, выделяют два вида движения:

• Прямолинейное — тело движется по прямой линии.
• Криволинейное — тело движется по кривой линии, в том числе замкнутой.

По скорости выделяют два вида движения:

• Равномерное — скорость движущегося тела остается неизменной.
• Неравномерное — скорость движущегося тела с течением времени меняется.

По ускорению выделяют три вида движения:

• Равноускоренное — тело движется неравномерно с постоянным ускорением (положительным). Скорость увеличивается.
• Равнозамедленное — тело движется неравномерно с постоянным замедлением (отрицательным ускорением). Скорость уменьшается.
• Ускоренное — тело движется неравномерно с меняющимся ускорением. Скорость может, как увеличиваться, так и уменьшаться.

Что нужно для описания механического движения?

Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.

Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.

Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.

Тело отсчета — тело, относительно которого рассматривается движение.

Часы — прибор для отсчета времени. Время измеряется в секундах (с).

При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.

Виды систем координат

В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:

• Одномерную. Используется, когда положение материальной точки можно задать только одной координатой x — M(x) . В этом случае тело движется прямолинейно.
• Двумерную. Используется, когда положение материальной точки можно задать двумя координатами x и y — M(x,y). Тело в этом случае движения по плоскости.
• Трехмерную. Используется, когда положение материальной точки можно задать тремя координатами x, y и z — M(x,y,z). Тело в этом случае изменяет положение в трехмерном пространстве.

Способы описания механического движения

Описать механическое движение можно двумя способами:

1. координатным
2. векторным

Координатный способ

Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:

Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.

Векторный способ

Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.

Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:

Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.

Характеристики механического движения

Движение материальной точки характеризуют три физические величины:

1. перемещение
2. скорость
3. ускорение

Перемещение

Определение

Перемещение (вектор перемещения) — направленный отрезок, начало которого совпадает с начальным положением точки, а конец — с его конечным положением. Обозначается как S .

Перемещение точки определяется как изменение радиус-вектора. Это изменение обозначается как Δ r . С точки зрения геометрии вектор перемещения равен разности радиус-векторов, задающих конечное и начальное положение точки:

Траектория — линия, которую описывает тело во время движения.

Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).

Путь есть функция времени:

Модуль перемещения — длина вектора перемещения. Обозначается как |Δ r |. Единица измерения — метры (м).

Модуль перемещения необязательно должен совпадать с длиной пути.

Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.

Путь равен длине окружности. Поэтому:

Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.

Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?

Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:

Скорость

Определение

Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.

В физике скорость обозначается V . Математически скорость определяется формулой:

Скорость характеризуется не только направлением вектора скорости, но и его модулем.

Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).

Математическое определение модуля скорости:

Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:

Ускорение

Определение

Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.

В физике ускорение обозначается a . Математически оно определяется формулой:

Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с 2 ).

Математическое определение модуля скорости:

v — скорость тела в данный момент времени, v0— его скорость в начальный момент времени, t — время, в течение которого эта скорость менялась.

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:

Проекция вектора перемещения на ось координат

Определение

Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.

Проекция вектора на ось OX:

Проекция вектора на ось OY:

Знаки проекций перемещения

• Проекция является положительной, если движение от начала проекции вектора к проекции конца происходит сонаправленно оси координат.
• Проекция является отрицательной, если движение от начала проекции вектора к проекции конца направлено в сторону, противоположную направлению координатной оси.

Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.

Модуль перемещения — длина вектора перемещения:

Модуль перемещения измеряется в метрах (м).

Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:

Выразив проекции вектора перемещения через координаты, эта формула примет вид:

Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:

Общий вид уравнений координат:

Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.

Определяем координаты начальной точки вектора:

Определяем координаты конечной точки вектора:

Проекция вектора перемещения на ось OX:

Проекция вектора перемещения на ось OY:

Применяем формулу для вычисления модуля вектора перемещения:

Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.

Извлекаем известные данные:

Для определения координаты точки В понадобятся формулы:

Выразим из них координаты конечного положения точки:

Точка В имеет координаты (5; 10).

Задание EF17612 Тело начинает двигаться из состояния покоя с ускорением 4 м/с 2 . Через 2 с его скорость будет равна.

Алгоритм решения

1. Записать исходные данные в определенной системе отсчета.
2. Записать формулу ускорения.
3. Выразить из формулы ускорения скорость.
4. Найти искомую величину.

Решение

Записываем исходные данные:

• Тело начинает двигаться из состояния покоя. Поэтому его начальная скорость v0 = 0 м/с.
• Ускорение, с которым тело начинает движение, равно: a = 4 м/с 2 .
• Время движения согласно условию задачи равно: t = 2 c.

Записываем формулу ускорения:

Так как начальная скорость равна 0, эта формула принимает вид:

Отсюда скорость равна:

Подставляем имеющиеся данные и вычисляем:

Источник: spadilo.ru