Что значит соотношение 1 к 2? Например, для приготовления овсяной каши обычно требуется стакан хлопьев на два стакана молока или воды. Получается соотношение 1 : 2 («один к двум» или «один стакан хлопьев на два стакана молока»).
Как правильно посчитать соотношение?
Процентное отношение определяет, какой процент от целого составляет данное число. Для нахождения процента нужно разделить одно число на другое и умножить на 100%. Пример: Процентное соотношение числа 25 от 50 будет составлять 50%, так как 25/50×100%=50%.
Что значит разбавить 1 к 2?
Например, если рецепт рекомендует смешать два раствора и воду в соотношении 1:2:5, это значит, что нужно взять один объем первого раствора, два таких же объема второго раствора и пять объемов воды, получив при этом восемь объемов смеси. . Например, 10%-ный раствор бромистого калия нужно развести водой до концентрации 2%.
Что значит соотношение 2 к 5?
Отношение не изменится, если члены его умножить или разделить на одно и то же число. Отношения 5 к 2 и 2 к 5, как и дроби 5 2 и 2 5 , называют взаимно обратными. Для нахождения отношения длин, отношения масс надо выразить их в одной единице измерения.
Как правильно разбавлять концентрированные составы? Пропорции 1:10 или 1:20
Как найти соотношение между числами?
Правило. Чтобы найти процентное отношение двух чисел , нужно одно число разделить на другое, а результат умножить на 100. Например, вычислить, сколько процентов составляет число 52 от числа 400.
Что значит развести 1 к 3?
Соотношение 1 к 3
Это соотношение подойдет для сбраживания при помощи специальных спиртовых дрожжей, которые выдерживают концентрацию спирта 15-20%. К примеру берем 1 килограмм сахара и 3 литра воды, общий объем у нас получается 4 литра, в процентном соотношении это получается 1*100/4=25% сахаристость сусла.
Что значит соотношение 1 к 3?
И при расчете пропорций, многие люди начинают путаться, поэтому давайте разберёмся, что понимается под пропорцией 1 к 3. . Это обозначает, что, например, на два литра молока вы должны класть две столовые ложки соли и шесть столовых ложек сахара, чтобы сохранялась требуемая пропорция: 2/6=1/3.
Что значит соотношение 2 к 3?
Понимание «Отношение чисел» используется для сравнения двух величин и показывает во сколько раз первое число больше второго, либо какую часть первое число составляет от второго. В нашем примере отношение показывает, что число 2 составляет 2/3 от числа 3. Отношение показывает, что число 5 составляет 1/2 от числа 10.
Как высчитать процент из трех чисел?
- 1% от числа = разделить число на 100 (1% от 200 = 200/100 = 2);
- 10% от числа = разделить число на 10 (10% от 200 = 200/10 = 20);
- 25% от числа = разделить число на 4 или два раза на 2 (25% от 200 = 200/4 = 50);
- 33% от числа ≈ разделить число на 3;
- 50% от числа = разделить число на 2.
Как посчитать соотношение 3 к 2?
Процентное соотношение
Если умножить все количества в соотношении на одно и то же число, то соотношение не изменится. Например, соотношение 3:2 есть то же самое, что 12:8.
Что такое отношение единицы к числу?
Частное двух чисел и , отличных от нуля, называют отношением числа к числу . Отношение числа к числу записывается как или . Пример: Отношение числа 6 к числу 2 равно . Это значит, что 6 — это 3 раза по 2.
Источник: krugruk.ru
Что такое пропорция
Математика учит нас равенству отношений. Пропорции — тема несложная, но важная. Давайте разберемся, что такое пропорция и как с ней обращаться.
17 декабря 2020
· Обновлено 28 октября 2022
Что такое пропорция
Пропорция — это равенство двух отношения.
Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.
Пропорция всегда содержит равные коэффициенты.
Если выразить определение формулой, то выглядеть оно будет так:
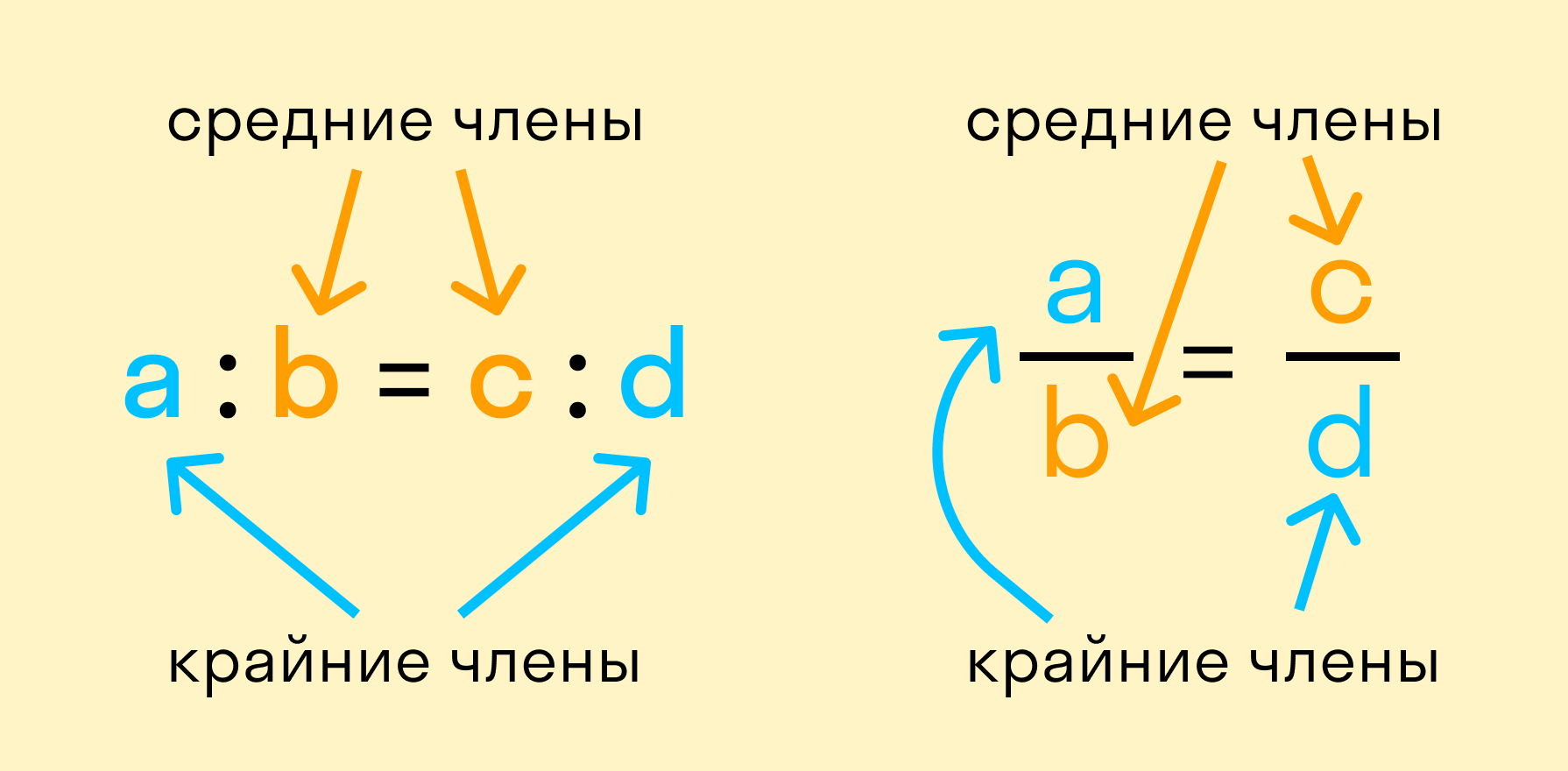
a и d — крайние члены пропорции, b и с — средние члены пропорции.
Читается это выражение так: a так относится к b, как c относится к d
Например:
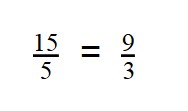
Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.
15 и 3 — крайние члены пропорции.
5 и 9 — средние члены пропорции.
Наглядный пример для понимания:
У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.

- Запишем эту непростую ситуацию в виде отношения 8 кусочков к 4 голодным друзьям: 8 : 4
- Далее преобразовываем это отношение в дробь: 8/4
- Выполняем деление: 8/4 = 2
Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!
А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.

Что мы имеем: 4 кусочка и 2 друга, претендующих на них.
- Запишем в виде отношения: 4 : 2
- Преобразовываем получившееся отношение в дробь: 4/2
- Выполняем деление: 4/2 = 2
Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.
Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.
Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным
Источник: skysmart.ru
Масштаб, соотношение чисел


Ученики шестого класса заинтересовались картой мира. Ребята, на перемене, стоя у доски, долго рассматривали океаны, материки, горные вершины, пустыни. После, перешли к изучению обозначений и символов, нанесенных на карту. Вдруг, Макар заметил, в верхнем правом углу рассматриваемого изображения, имеются непонятные цифры – 1:20 000 000.
Мальчик спросил у одноклассников, что обозначает странная надпись на карте. Школьники не смогли дать ответ на вопрос Макара. В этот момент прозвенел звонок, в класс вошел учитель. Мальчик поднял руку и задал свой вопрос. Учитель объяснил детям, что цифры на карте обозначают масштаб, то есть, отношение размера рисунка к реальному размеру.
Проще говоря, запись 1:20 000 000 показывает, что отрезок в 1см на карте соответствует отрезку 20 000 000 см на местности. И посоветовала ребятам внимательно изучить тему отношения и пропорции на сайте «100urokov.ru». Сегодня на уроке рассмотрим, на простых и понятных примерах, как найти отношение двух чисел, как звучит определение пропорции, что такое прямая и обратная пропорциональная зависимость, и что скрывается за непонятным словом «масштаб».


План урока:
Отношение двух чисел
На уроке математики ребята выполняли самостоятельную работу. На решение самостоятельных заданий Наталья Ивановна выделила 15 минут, после чего попросила сдать тетради на проверку. Подумайте, какую часть урока заняла самостоятельная работа?

Чтобы дать ответ на данное задание, давайте вспомним, какую продолжительность имеет обычный урок? Всем известно, что стандартный урок длится 45 минут. Получается, из 45 минут только 15 дети решали самостоятельную работу. Следовательно, нужно выяснить, какая часть целого урока потрачена на самостоятельную работу. В арифметике для вычисления части от числа или определения во сколько раз одно число больше другого существует специальное понятие «Отношение чисел»:

Исходя из рассмотренного определения, необходимо составить отношение длительности самостоятельной работы к длительности целого урока. Таким образом, ответим на главный вопрос задачи. Запишем отношение (частное) двух чисел:
15/45 – данную дробь можно сократить, разделив числитель и знаменатель на 15.
Выходит, что на самостоятельную работу класс потратил 1/3 всего урока.
Важно помнить, что числовое значение отношения чисел останется прежним, если каждый компонент отношения умножить или разделить на одно и то же число.
Давайте, составляющие отношения 6/7 умножим на 2, то есть на дробь 2/2.
6/7 × 2/2 (числитель умножаем на числитель, знаменатель на знаменатель);
6×2/7×2 = 12/14 – при сокращении на 2, получим исходную дробь.
Следовательно, числовое значение дроби не изменилось – 6/7 = 12/14.
При составлении отношений с использованием различных чисел и величин, важно помнить, что отношение будет верным, если все компоненты отношения выражены в одинаковых единицах измерения.
Разберем на примере.
В вазочке находился один килограмм конфет. Бабушка отсыпала 300 граммов сладостей в пакет. Определите, какую часть всех конфет отсыпала бабушка?

Чтобы ответить на главный вопрос задачи нужно составить отношение массы отсыпанных конфет к общей массе сладостей: 300 граммов/1 килограмм. Сразу определить числовое значение отношения не можем, составляющие имеют разные единицы измерения массы – грамм и килограмм. Выразим один килограмм в граммах:
1кг = 1000 грамм
Теперь определим, какую часть составили отсыпанные сладости:

Бабушка отсыпала 3/10 всех сладостей в пакет.
Запомни!
Если a и b числовые значения или значения, выраженные в одной и той же величине, тогда:
- отношение a/b, будет равно частному a и b;
- при условии, что a>b, отношение a/b говорит, во сколько раз a больше, чем b;
- при условии, что a
Определение пропорции
Руководитель детского хореографического кружка, для пошива костюмов своим воспитанникам, приобрел в магазине тканей 10 метров шелка, на сумму 420 рублей. Но купленной ткани не хватило. Какую сумму нужно потратить, чтобы купить еще 5 метров такого же материала?

Данную задачу можно решить двумя способами. Рассмотрим каждый из них подробно.
По условию нам известно, что 10 метров материала, стоит 420 рублей. Отсюда можно узнать цену одного метра. Для этого, общую сумму(420) необходимо разделить на количество приобретенной ткани(10):
420 : 10 = 42 рубля стоит один метр ткани.
Зная цену одного метра ткани, можно узнать стоимость пяти метров. Для этого стоимость одного метра (42), умножаем на количество таких метров (5):
42 × 5 = 210 рублей необходимо, для покупки 5 метров материала.
Этот способ известен еще из начальной школы. Но далеко не все задачи такого вида можно решить первым способом.
В этом случае используют второй способ решения задач такого вида.
Вначале, запишем краткое условие.
Теперь нужно подумать. В нашем случае, количество материала уменьшается, следовательно,уменьшается стоимость покупки. Обозначим цену пяти метров материала – х.
Для решения задач такого вида в математике существует специальное определение – «Пропорция»

Используя рассмотренное определение, подумаем, как составить пропорцию из чисел? Формировать пропорцию будем, опираясь на краткую запись условия задачи – десять относится к пяти как четыреста двадцать к иксу:
Пропорция составлена и возникает вопрос, как вычислить неизвестный компонент?
Для вычисления неизвестной составляющей пропорции существует правило, которое называется «Основное свойство пропорции»:

Определим крайние и средние члены в составленном равенстве:
Крайними членами пропорции будут числа 10, х.
Средними членами пропорции будут числа 5, 420.
Запишем равенство произведений крайних и средних членов в составленной пропорции:
10х = 5 × 420 – высчитываем произведение;
10х = 2100 – решаем как обычное уравнение;
Выходит, 210 рублей необходимо для приобретения пяти метров материала.
Вот так на примере решения задачи мы разобрали новое определение. Запомните, пожалуйста, все правила и поиск неизвестного компонента в любых отношениях и пропорциях будет для вас только развлечением!
Продолжаем дальше знакомиться с пропорцией.
Прямая и обратная пропорциональная зависимость.
Рассмотрим ситуацию, в которой оказывается каждый, попадая в магазин.

Витя пришел в магазин за покупками. В кошельке ребенка лежало 300 рублей. Витя купил хлеб, молоко, масло, заплатил за товар. Денег у мальчика стало меньше. После посещения кондитерского отдела, где он купил карамель, пирожные, рулет денег стало совсем мало.
Делаем вывод: чем больше покупок делает мальчик, тем меньше денег у него остается.

Значит, количество денег в нашем кошельке и количество покупок имеют обратно пропорциональную зависимость и являются обратно пропорциональными величинами.
А если взять ситуацию с оплатой за пользование водой и электроэнергией

Чем больше воды/электроэнергии мы используем, тем больше должны заплатить. В таком случае величины кубы воды/киловатты электроэнергии и денежные единицы называются прямо пропорциональными и имеют прямую пропорциональную зависимость.

Масштаб
Мама с Арсением решили нарисовать путь, который проходит мальчик, идя из дома в школу. Ребенок заволновался: «Как можно на листке бумаги нарисовать 450 метров пути?». Мама успокоила сына и рассказала, что именно для таких случаев и используется определение масштаба карты.

Рассмотрим решение задачи с использованием масштаба.
Расстояние на карте от Москвы до Киева составляет пять сантиметров. Вычислите, сколько километров от Москвы до Киева, если масштаб карты 1:15 000 000.

В первую очередь, нужно понимать, что масштаб 1:15 000 000 показывает, что 1 см карты содержит 15 000 000 сантиметров или 150 километров на местности.
Чтобы ответить на главный вопрос задачи,составим пропорцию. Для этого, расстояние на местности от Москвы до Киева примем за х:
Помним, произведение крайних членов пропорции равно произведению средних. Имеем:
Выходит, 750 километров – расстояние от Москвы до Киева.
Расчеты оказались верными. Вся справочная литература говорит о том, что расстояние Москва – Киев составляет примерно 755 км!
Теперь вы совершенно самостоятельно можете рассчитать абсолютно любое расстояние, имея под рукой линейку и карту!
Интересно!
С пропорциями мы сталкиваемся, ежедневно, ежеминутно. Все в нашем мире пропорционально. Любая вещь, предмет, техника, животные, растения – все имеет свои пропорции! Мы можем любоваться красивой архитектурой – благодаря пропорциям, наслаждаться цветками роз или ромашек – тоже не без участия пропорций. Природа создает все в строгой пропорциональности.
В случае, когда пропорции отсутствуют, вещь или предмет нам кажутся неправильными. Ведь даже в нашем теле все имеет свои пропорции:
- длина ладони равна длине четырех пальцев, длина четырех ладошек(без учета пальцев) равна длине стопы, шесть ладоней – длина локтя, а четыре локтя в точности укажут на рост хозяина;
- длина человеческой ладони с пальцами составляет 1/10 роста человека;
- длина расставленных в стороны рук совпадает с длиной человеческого тела;
- стопа составляет 1/7 часть роста;
- длина от корней волос до кончика подбородка равна 1/10 роста.
Источник: 100urokov.ru
Пропорция.
Поскольку 3,6 : 0,9 = 4 и 1,2 : 0,3 = 4, то верно и равенство 3,6 : 0,9 = 1,2 : 0,3, которое называют пропорцией ( от лат. ргоро rtio — «соизмеримость» ).
Поскольку 3,6 : 0,9 = 4 и 1,2 : 0,3 = 4, то верно и равенство 3,6 : 0,9 = 1,2 : 0,3, которое называют пропорцией (от лат. ргороrtio — «соизмеримость»).
Если соотношение а : b равно соотношению с : d, то тождество а : b = с:d называют пропорцией.
Пропорцию можно выразить также в виде:
Приведённые записи читают: «соотношение а к b равно соотношению с к d или «а соотносится к b, как с соотносится к d».
Числа a и d именуют крайними членами пропорции, числа b и с — средними членами пропорции.
В пропорции 3,6 : 0,9 = 1,2 : 0,3 числа 3,6 и 0,3 — крайние члены, числа 0,9 и 1,2 — средние члены. Рассмотрим произведение крайних и средних членов 3,6•0,3 = 0,9 • 1,2
Такая особенность присуща каждой пропорции и именуется главная особенность пропорции — произведение крайних членов пропорции равно произведению её средних членов.
Это определяется так:
если , то ad = bc
Главную особенность пропорции еще именуют правилом креста. Следуя главной особенности пропорции, можно рассчитать ее неизвестный член, если все остальные члены определены.
Чтобы определить неизвестный крайний член пропорции, необходимо произведение средних членов пропорции поделить на известный крайний член.
Чтобы определить неизвестный средний член пропорции, необходимо произведение крайних членов пропорции поделить на известный средний член. Или обобщенно можно сформулировать так: чтобы вычислить неизвестный член пропорции, следует перемножить диагональ с обоими известными членами, а далее поделить на оставшееся известное значение.
Правильна и следующая формулировка: если а, b, с и d числа отличные от нуля, то для них верно:
если , то
эта особенность называется свойством обращения пропорции.
Если в верной пропорции поменять местами средние члены или
крайние члены, то получившиеся новые пропорции тоже верны. Это свойство перестановки крайних и средних членов пропорции.
Если , то
(перестановка средних членов пропорции),
(перестановка крайних членов пропорции).
Так же на практике пользуются правилом увеличения и уменьшения пропорции.
Если , то равенство сохранится и в следующих случаях:
(увеличение пропорции),
(уменьшение пропорции).
Составление пропорции сложением и вычитанием .
Если , то
(составление пропорции сложением),
(составление пропорции вычитанием).
Обратим внимание, что составление пропорций — ещё один способ решения задач на проценты.
Олово производят из минерала, который называют касситеритом. Сколько тонн олова получат из 25 т касситерита, если он содержит 78 % олова?
Решение. Пусть получат х т олова. Взяв массу минерала за 100 % , запишем:
Решив 25•78 = 100х мы находим, что х = 19,5т.
Концепция пропорции тесно взаимосвязана с пропорциональностью. Пропорциональность — это неизменное соотношение двух величин друг к другу. Например, чем больше мы давим на педаль «газ» в машине, тем стремительнее она поедет.
Пропорциональность может быть прямой и обратной.
Прямая пропорциональность -рост одной величины влечет за собой рост другой.
Обратная пропорциональность существует тогда, когда рост одной величины в несколько раз, во столько же раз уменьшает другую. Продолжая предыдущий пример — обратная пропорциональность между нажатием на педаль «тормоз» и скоростью автомобиля — чем больше мы давим на тормоз, тем меньше скорость.
Источник: www.calc.ru
