Что означает дробь 2 3

Дробь в арифметике — число, состоящее из одной или нескольких равных частей (долей) единицы [1] .

В математике используется несколько обобщённое определение, различающее два типа дробей.

1. Обыкновенные дроби[⇨] вида m n >> , где m целое, n натуральное. В отличие от арифметического определения, такая дробь может иметь знак минус.
2. Запись (не обязательно дробных) чисел в позиционных системах счисления. Наиболее известны десятичные дроби
3. [⇨] , удобные для людей, и двоичные дроби, которые используются для расчётов на компьютерах [2] .

В математической записи дроби вида m / n или m n >> число перед (над) чертой называется числителем, а число после черты (под чертой) — знаменателем. Первый выступает в роли делимого, второй — делителя.

• 1 Виды дробей

• 1.1 Обыкновенные дроби

• 1.1.1 Обозначения обыкновенных дробей
• 1.1.2 Правильные и неправильные дроби
• 1.1.3 Смешанные дроби
• 1.1.4 Составные дроби

• 3.1 Приведение к общему знаменателю
• 3.2 Сравнение
• 3.3 Сложение и вычитание
• 3.4 Умножение и деление
• 3.5 Возведение в степень и извлечение корня
• 3.6 Преобразование между разными форматами записи

Источник: wiki2.org

2/3 части это сколько? Две третьи, это сколько?

Обыкновенная дробь 2/3, знаменатель говорит от том, что что-то целое разделили на 3 равные части, а числитель — что взяли из этих трех частей только 2. Оставшаяся часть будет 1/3 (одна часть из трех, одна третья) В процентах 2/3 это 66,6666. % или 66,(6)% — число 6 в периоде (иррациональное число).

габбас [151K] 2 года назад

2/3 части какого-либо значения величины означает, что это значение нужно разделить на 3 и умножить на 2. Например, две третьи от числа 24 будет равна 16, 24:3 = 8, 8*2 = 16. Так же находим 2/3 любого другого числа или величины. Например, 2/3 площади квартиры, если площадь равна 40 кв. метрам, то 2/3 от этой площади будет равна 40 кв. метрам. Не любое число делится на 3, поэтому часто получаются дробные значения или бесконечные десятичные дроби при нахождение 2/3 части. Например, две трети 100, это примерно 66,7.

чтобы возвести дробь в степень надо возвести в степень и числитель и знаменатель Результатом возведения дроби в степень будет новая дробь у которой числитель равен числителю этой дроби в возведенному в степень, а знаменателем будет знаменатель этой дроби в возведенный в степень. Пример

(¾)³=3³/4³=27/64

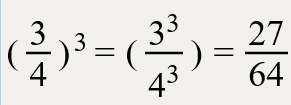
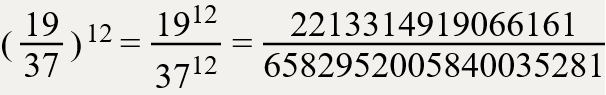
2 года назад

Представьте себе, приехали Вы, допустим, в Африку. Разбили палатку, лежите в шезлонге, наслаждаетесь видом восхода, попивая через трубочку свежее кокосовое молоко. И тут приходят к Вам два туземца с разных племён, разрешить им спор, кто из них более удачлив в охоте на кабана. Один их них говорит, что добыл кабана весом в 129 квортов, а другой — весом в 366 умагов. И как быть?

Чей кабан тяжелее? Тогда Вы, выяснив, ‘курс’ кворта и умага к привычному Вам килограмму, переводите оба веса в килограммы. Только тут становиться ясно, кто из охотников более удачлив. Так и с дробями. Дроби с разными знаменателями сродни измерению в разных системах.

Сами по себе они могут так жить преспокойно, со своими уникальными знаменателями, пока не придёт время их сравнить, или сложить. Вот тут то и нужно их привести к чему-то одному, ‘компромиссному’. При переводе к единому знаменателю числители у этих дробей и выйдут тогда из ‘сумерка’, показав свой истинный вес.

2 года назад

Как увидел задание сразу подумал, что оно явно не на тупое умножение, тем более перемножение всех чисел даст примерно двадцатитысячезначное число. Прикинул какие числа входят в состав множителей и оказалось, что там есть число (при чем оно не одно, но достаточно было бы и одного) наличие которого однозначно определяет последнюю цифру результата — это число 5, так как при умножении на пять любого нечетного числа последней цифрой будет опять таки пять: 1*5=5, 3*5=15, 5*5=25, 7*5=35, 9*5=45, если в числах присутствуют помимо низшего разряда более высокие — десятки, сотни и т.д., то они ни как не могут повлиять на разряд единиц, поэтому их можно не рассматривать. Также можно добавить, что величина числа, до которого надо все нечетные числа (в задании это 9999), ни как не влияет на результат последней цифры если такое число 5 или более. Также добавлю, что для четных чисел ответ на такое же задание будет 0, так как там присутствует как минимум одно число заканчивающееся на 0, например 10.

2 года назад

Здесь можно только сократить, по формуле разности квадратов. Нужно представить в виде c=(√с)^2, и 3=(√3)^2. Тогда числитель (с-3) можно представить в виде ((√с)^2-(√3)^2) и разложить его на множители в виде (√с-√3)*(√с+√3). Теперь в числителе есть одинаковый со знаменателем множитель, и на него можно сократить. Остаётся (√с-√3).

2 года назад

Ну если это уравнение с параметром, то нужно еще доп. сведение, если трансцендентное уравнение, то решение проблематичное, ибо надо заниматься подстановкой. Однако кое-что все же ясно. X надо найти, а вот «a» яко бы известно.

1) Нарисовать график, допустим y=3,335; 2) Нарисовать график, x/a, где a — параметр, который можно задать, посмотреть варианты удобного пересечения y=3,335, и x/a, в итоге x — то что можно найти. P.S.

Представим, что это трансцендентное уравнение, тогда решение примет примет вид: f(x)=g(x)=y, где f(x)=y=x/a, а g(x)=y=3,335, нарисуем на графике g(x)=3,335=y, полученная кривая — прямая линия, тогда становится очевидно, что f(x)=x/a, должна пересекать g(x) в некоторой точке (у,x) и при том в единственной, т.к. f(x)=x/a — тоже уравнение прямой, где x — аргумент (изменяется вдоль оси абсцис), а «а» константа. P.P.S.

Для решения используем калькулятор или ПО Excel, что бы облегчить ПодбоР! корня. Также используем метод последовательных приближений с заданным интервалом вдоль явного решение, которое соответственно равно g(x)=y=3,335. Т.к. f(x)=x/a начнем подбор x и «а» одновременно. Итерация 1: x/a=17/5=3,4 — подход справа, x/a=16/5=3,2 — подход слева!

Продолжая последующие итерации, постоянно увеличивая приближения от десятых до сотых и тысячных, находим значение константы «a» и корня x. Итерация IJK: x/a=3335/1000=3,335, так как любую дробь можно сократить, например x/a=6,67/2=3,335/1, то корнем могло явится и это уравнение и любое другое, аналогичное, однако в трансцендентных уравнениях, корень, т.е. x обычно целое число — это особый подвид трансцендентных уравнениях в целых числах. X=3335, a=1000.

P.P.P.S Если же это уравнение с параметром или что более верно уравнение с буквенной частью, то все еще проще: x/a=3,335 => x=3,335*a — уравнение прямой, где «a» произвольная константа. P.P.P.P.S. В случаи, если это все же уравнение с параметром и доп. задание, при каких значениях аргумента x, уравнение имеет смысл, то ответ при любых — этот вывод, мы получили, когда решали трансцендентное уравнение. Напоследок, безусловно для любого решения «a» не равно нулю, в математике это важно, но все же не считаю я нужным это указать, т.к. мы явно установили вид кривой и явно указали 1 точку пересечения, если б деление было бы на ноль возможно, то первые два утверждения были бы автоматически не верны.

2 года назад
Смотрите также:
Как узнать на сколько процентов одно число больше другого?

5 · 10 ответов · школа

Сумма обратных величин каких 2015 натуральных чисел будет равна 1?

0 · 1 ответ · математика

1/3 часть это сколько? Одна третья, это сколько?

5 · 10 ответов · ответы

Как сложить и вычесть дроби/рациональные дроби с одинаковыми знаменателями?

2 · 2 ответа · школа

1/5 часть это сколько? Одна пятая, это сколько?

3 · 11 ответов · математика

1/9 часть это сколько? Одна девятая, это сколько?

2 · 10 ответов · математика

1/10 часть это сколько? Одна десятая, это сколько?

3 · 11 ответов · математика

3/4 части это сколько? Три четвертых части это сколько?

1 · 2 ответа · математика

Что значит соотношение 1 к 1, 1 к 2, 1 к 3 (или 1:1, 1:2, 1:3)?

6 · 11 ответов · математика

Являются ли зиллион и зиллиард числами?

3 · 4 ответа · математика

Источник: otvet.ya.guru

Что такое 2/3 в дроби?

Отсюда, что означают 2/3? также две трети. количественно Две трети чего-либо — это сумма, которая составляет две из трех равных частей.

Является ли 2/3 неправильной дробью? Объяснение: у неправильной дроби числитель больше знаменателя. У правильной дроби числитель меньше знаменателя. Так, 23 — правильная дробь.

Похожие страницы:Блог

Какие есть 3 вида налогов?

Как найти среднюю точку между двумя точками?

Как вы делаете кадровые прогнозы?

Как найти начальную скорость, зная только время?

Дополнительно Что такое 2/3 целого? Чтобы найти 2/3 целого числа, мы должны умножить число на 2 и разделить его на 3. Чтобы найти две трети от 18, умножьте 2/3 x 18/1, чтобы получить 36/3.

Что такое 2/3 в виде смешанной дроби? Так как 23 — правильная дробь, это не может быть записано как смешанное число.

Как превратить 3 2 в смешанное число?

Поскольку 3/2 — неправильная дробь, то, разделив 3 на 2, мы получим 1 как частное и 1 как остаток. Чтобы преобразовать неправильную дробь в смешанную, возьмем в качестве целой части частное 1 и в остатке дробной части 1 в качестве числителя, а делитель 2 в качестве знаменателя. GCF 1 и 2 равен 1.

Что такое 2 и 2/3 как неправильная дробь? Неправильная дробь 8/3 равно смешанному числу 2 2/3.

Что такое 2/3 в простейшей форме?

Как превратить 2 3 в целое число?

2/3 при переводе в десятичные дроби будут равны 0.66 то есть при округлении до ближайшего целого числа будет равно 1, поскольку значение после запятой больше 5, поэтому оно будет округлено до ближайшего целого числа. Следовательно, 2/3 как целое число будет равно 1.

Также как написать 2/3 как неправильную дробь?

Что такое 1 и 2/3 как неправильная дробь?

Ответ и пояснение: Смешанное число 1 2/3 — это 5/3 как неправильная дробь.

Что такое 3 и 2/3 как дробь? Неправильная дробь, равная смешанному числу 3 2/3, называется 11/3.

Что такое 2/3 в виде десятичной дроби?

Ответ: Десятичная форма 2/3 равна 0.666.

Как найти 3 2 числа?

Разделите количество интересов на 3. Если вы нашли две трети от 60, то сначала разделите 60 на 3. В результате вы получите число 20.

Что такое 3 и 2/3 как неправильная дробь? Неправильная дробь, равная смешанному числу 3 2/3, называется 11/3.

Что такое 8 и 2/3 как неправильная дробь? Сначала преобразуйте смешанное число 823 8 2 3 в неправильную дробь, умножив знаменатель (3) на целую часть (8) и добавив числитель (2), чтобы получить новый числитель. Поместите новый числитель (26) над старым знаменателем (3).

Как упростить 2 3 3?

Что означает 2/3 как десятичная дробь? Ответ: Десятичная форма числа 2/3 0.666.

Какая дробь не равна 2 3?

Ответ: 2/3 = 2×4 / 3×4 = 8/12 что эквивалентно дроби 2/3. Точно так же, если мы разделим числитель и знаменатель 12/18 на 6, мы получим. 12/18 = 12÷6 / 18÷6 = 2/3.

Чему равно 2/3 как дробь от 100? Наша процентная доля 66.666666666667/100, что означает, что 23 в процентах составляет 66.67%.

Как смешанное число превратить в дробь?

Как смешанную дробь превратить в простую? Ответ: Чтобы смешанное число превратить в неправильную дробь, умножьте целое число на знаменатель правильной дроби. Добавьте к этому произведению числитель правильной дроби, чтобы получить числитель неправильной дроби.

Что такое 2 с половиной как неправильная дробь?

212 как неправильная дробь 52 .

Как превратить 10.5 в дробь? Шаги для преобразования десятичной дроби в дробь

1. Запишите 10.5 как 10.51.
2. 10.5 × 101 × 10 = 10510.
3. 212

Как решить смешанные дроби?

Источник: reviews.tn

ОБЫКНОВЕННАЯ ДРОБЬ

Ключевые слова конспекта: дроби, обыкновенная дробь, правильные и неправильные дроби, основное свойство дроби, сравнение дробей, арифметические действия с дробями, нахождение части от целого и целого по его части.

Содержание (быстрый переход): Скрыть

Одна или несколько равных частей единицы называются обыкновенной дробью. Дробь 3/4 означает, что единицу разделили на 4 части и взяли 3 таких части.

Дробь можно рассматривать и как результат деления натуральных чисел. Частное от деления натуральных чисел а и b можно записать в виде дроби a/b — где делимое а — числитель, а делитель b — знаменатель.

Правильная и неправильная дробь

Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.

Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.

Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.

Основное свойство дроби

Определение. Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной.

Основное свойство дроби используют при сокращении дробей. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дробей.

Сравнение дробей

1. Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
2. Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

• привести дроби к наименьшему общему знаменателю;
• сравнить полученные дроби.

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

1. найти наименьшее общее кратное (НОК) знаменателей дробей (оно и будет их общим знаменателем);
2. разделить общий знаменатель на знаменатель данных дробей, т. е. найти для каждой дроби дополнительный множитель;
3. умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Арифметические действия с обыкновенными дробями

Сложение и вычитание дробей

При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.

При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.

Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!

Общий случай сложения (вычитания) дробей.

Умножение дробей

1. Произведение двух дробей a/b и c/d равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
2. При умножении чисел, состоящих из целой и дробной частей, их предварительно представляют в виде неправильных дробей, а затем умножают согласно п. 1.

Деление дробей

Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.

При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.

Нахождение части от целого (дроби от числа)

Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель дроби, выражающей эту часть, и результат умножить на числитель той же дроби.

Задача нахождения части от целого по существу является задачей нахождения дроби от числа. Чтобы найти дробь (часть) от числа, необходимо число умножить на эту дробь.

Нахождение целого по его части (числа по его дроби)

Чтобы найти целое по его части, нужно число, соответствующее этой части, разделить на числитель дроби, выражающей эту часть, и результат умножить на знаменатель той же дроби.

Задача нахождения целого по его части по существу является задачей нахождения числа по его дроби. Чтобы найти число по его дроби, необходимо данное значение разделить на эту дробь.

Это конспект по теме «Обыкновенная дробь». Выберите дальнейшие действия:

Источник: uchitel.pro