Дано:
$m = 300 space г$
$Delta t = 200 degree C$
$c = 460 frac$
СИ:
$m = 0.3 space кг$
Показать решение и ответ
Решение:
Для того чтобы нагреть железную деталь, необходимо сообщить ей некоторое количество теплоты:
$Q = cm(t_2 — t_1) = cm Delta t$.
Рассчитаем эту энергию:
$Q = 460 frac cdot 0.3 space кг cdot 200 degree C = 27 space 600 space Дж = 27.6 space кДж$.
Сообщенная энергия будет эквивалентна работе внешних сил:
$A = Q = 27.6 space кДж$.
Ответ: $A = 27.6 space кДж$.
Задача №2
Приняв, что вся тепловая энергия угля обращается в полезную работу, рассчитайте какого количества каменного угля в час достаточно для машины мощностью $733 space Вт$?
Дано:
$t = 1 space ч$
$N = 733 space Вт$
$q = 2.7 cdot 10^7 frac$
СИ:
$t = 3600 space с$
Показать решение и ответ
Решение:
Мощность по определению:
$N = frac$.
Выразим отсюда полезную работу, совершаемую машиной, и рассчитаем ее:
На что способен пневматический пистолет до 3 ДЖоулей?
$A_п = Nt$,
$A_п = 733 space Вт cdot 3600 space с = 2 space 638 space 800 space Дж approx 0.26 cdot 10^7 space Дж$.
По условиям задачи количество теплоты, которое выделяется при сжигании каменного угля, равно полезной работе:
$A_п = Q = qm$.
Выразим отсюда массу угля и рассчитаем ее:
$m = frac$,
$m = frac> approx 0.1 space кг approx 100 space г$.
Ответ: $m approx 100 space г$.
Задача №3
Нагреватель за некоторое время отдает тепловому двигателю количество теплоты, равное $120 space кДж$. Тепловой двигатель совершает при этом полезную работу $30 space кДж$. Определите КПД теплового двигателя.
Дано:
$Q_1 = 120 space кДж$
$A_п = 30 space кДж$
СИ:
$Q_1 = 120 cdot 10^3 space Дж$
$A_п = 30 cdot 10^3 space Дж$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$eta = frac$.
Ответ: $eta = 25 %$.
Задача №4
Нагреватель отдает тепловому двигателю за $30 space мин$ количество теплоты, равное $460 space МДж$, а тепловой двигатель отдает количество теплоты, равное $280 space МДж$. Определите полезную мощность двигателя.
Дано:
$t = 30 space мин$
$Q_1 = 460 space МДж$
$Q_2 = 280 space МДж$
СИ:
$t = 1800 space с$
$Q_1 = 460 cdot 10^6 space Дж$
$Q_2 = 280 cdot 10^6 space Дж$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$eta = =frac = frac$, где
$A_п$ — полезная работа,
$Q_1$ — количество теплоты, полученное от нагревателя,
$Q_2$ — количество теплоты, отданное холодильнику.
Из этой формулы, мы можем сделать вывод, что $Q_1 — Q_2 = A_п$ — количество теплоты, которое пошло на совершение работы.
Величина работы также присутствует в определении мощности:
$N = frac$.
Пневматика до 3 джоулей
Когда мощность определяется полезной работой, мы называем ее полезной мощностью.
Подставим в формулу мощности определение работы из формулы для КПД и рассчитаем ее:
$N = frac$,
$N = frac = frac = 0.1 cdot 10^6 space Вт = 100 space кВт$.
Ответ: $N = 100 space кВт$.
Задача №5
Паровой молот мощностью $367 space кВт$ получает от нагревателя в час количество теплоты, равное $6720 space МДж$. Какое количество теплоты в час получает холодильник?
Дано:
$N = 367 space кВт$
$t = 1 space ч$
$Q_1 = 6720 space МДж$
СИ:
$N = 367 cdot 10^3 space Вт$
$t = 3600 space с$
$Q_1 = 6720 cdot 10^6 space Дж$
Показать решение и ответ
Решение:
Полезная работа, совершенная тепловым двигателем, определяется разностью количества теплоты, отданному холодильнику, и количества теплоты, полученного от нагревателя:
$A_п = Q_1 — Q_2$.
Тогда, количество теплоты, которое получает холодильник будет равно:
$Q_2 = Q_1 — A_п$.
Совершенную работу мы можем определить через мощность:
$N = frac$,
$A_п = Nt$.
Подставим в формулу для количества теплоты, получаемого холодильником:
$Q_2 = Q_1 — Nt$.
Рассчитаем эту энергию:
$Q_2 = 6720 cdot 10^6 space Дж — 367 cdot 10^3 space Вт cdot 3600 space с = 6720 cdot 10^6 space Дж — 1321.2 cdot 10^6 space Дж = 5398.8 cdot 10^6 space Дж approx 5400 space МДж$.
Ответ: $Q_2 approx 5400 space МДж$.
Задача №6
Мопед, едущий со скоростью $20 frac$, за $100 space км$ пути расходует $1 space кг$ бензина. КПД его двигателя равен $22 %$. Какова полезная мощность двигателя?
Дано:
$upsilon = 20 frac$
$s = 100 space км$
$m = 1 space кг$
$eta = 22 % = 0.22$
$q = 4.6 cdot 10^7 frac$
СИ:
$upsilon approx 5.6 frac$
$s = 100 cdot 10^3 space м$
Показать решение и ответ
Решение:
Мощность по определению:
$N = frac$.
Полезную работу мы можем выразить из формулы для расчета КПД теплового двигателя:
$eta = frac$.
Количество теплоты $Q_1$, выделившееся при сгорании бензина, мы можем найти по формуле:
$Q = qm$.
Подставим в формулу для расчета КПД:
$eta = frac$.
Выразим отсюда полезную работу:
$A_п = eta cdot qm$.
Время, которое необходимо нам для расчета мощности, мы можем найти через перемещение и скорость:
$t = frac<upsilon>$.
Подставим найденные формулы для величин $A_п$ и $t$ в формулу для расчета мощности:
$N = frac<upsilon>> = frac$.
Ответ: $N approx 567 space Вт$.
Задача №7
Определите КПД двигателя внутреннего сгорания мощностью $36.6 space кВт$, который сжигает в течение одного часа $10 space кг$ нефти.
Дано:
$N = 36.6 space кВт$
$t = 1 space ч$
$m = 10 space кг$
$q = 4.4 cdot 10^7 frac$
СИ:
$N = 36.6 cdot 10^3 space Вт$
$t = 3600 space с$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$eta = frac cdot 100 %$.
Полезную работу, совершенную двигателем мы можем определить через его мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Количество теплоты $Q_1$, полученное от нагревателя, — это энергия, которая выделится при сгорании топлива:
$Q_1 = qm$.
Ответ: $eta approx 30 %$.
Задача №8
Паровая машина мощностью $220 space кВт$ имеет КПД $15 %$. Сколько каменного угля сгорает в ее топке за $8 space ч$?
Дано:
$N = 220 space кВт$
$t = 8 space ч$
$eta = 15 % = 0.15$
$q = 2.7 cdot 10^7 frac$
СИ:
$N = 220 cdot 10^3 space Вт$
$t = 28.8 cdot 10^3 space с$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД:
$eta = frac$.
Полезную работу $A_п$ мы можем выразить через мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Количество теплоты, полученное от нагревателя — это энергия, выделившаяся при сгорании каменного угля:
$Q_1 = qm$.
Подставим эти выражения в формулу для КПД:
$eta = frac$.
Выразим отсюда массу каменного угля:
$m = frac$.
Ответ: $m approx 1564 space кг$.
Задача №9
Современные паровые механизмы расходуют $12.57 space МДж$ в час на $735 space Вт$. Вычислите КПД таких механизмов.
Дано:
$Q_1 = 12.57 space МДж$
$t = 1 space ч$
$N = 735 space Вт$
СИ:
$Q_1 = 12.57 cdot 10^6 space Дж$
$t = 3600 space с$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$eta = frac cdot 100 %$.
Полезную работу, совершенную двигателем мы можем определить через его мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Количество теплоты $Q_1$, полученное от нагревателя, нам дано в условиях задачи.
Подставим выражение для полезной работы в формула для КПД и рассчитаем его:
$eta = frac cdot 100 %$,
$eta = frac cdot 100 % approx 21 %$.
Ответ: $eta approx 21 %$.
Задача №10
Мощность дизельного двигателя $367 space кВт$, КПД $30 %$. На сколько суток непрерывной работы хватит запаса нефти $60 space т$ такому двигателю?
Дано:
$N = 367 space кВт$
$m = 60 space т$
$eta = 30 % = 0.3$
$q = 4.4 cdot 10^7 frac$
СИ:
$N = 367 cdot 10^3 space Вт$
$m = 60 cdot 10^3 space кг$
Показать решение и ответ
Решение:
Формула для расчета КПД теплового двигателя:
$eta = frac$.
Полезную работу $A_п$ мы можем выразить через мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Количество теплоты, полученное от нагревателя — это энергия, выделившаяся при сгорании нефти:
$Q_1 = qm$.
Подставим эти выражения в формулу для КПД:
$eta = frac$.
Выразим отсюда время, за которое была совершена полезная работа:
$t = frac$.
Переведем в сутки. В одном дне $60 cdot 60 cdot 24 space с = 86 space 400 space с$. Тогда,
$t = frac = 25 space сут$.
Ответ: $t = 25 space сут$.
Источник: obrazavr.ru
3 кдж сколько дж
НАВИГАЦИЯ ПО САЙТУ:
3.9 Закон Джоуля — Ленца.
Теория: При прохождении электрического тока через проводник, проводник нагревается (утюг, плойка, паяльник).
Закон Джоуля — Ленца: Количество теплоты выделяемое проводником с током равно произведению квадрата силы тока на сопротивление проводника и на время прохождения электрического тока. Q=I 2 Rt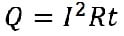 
Или с учетом закона Ома: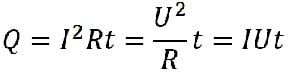 
Задание огэ по физике (фипи): Какое количество теплоты выделяется за 10 мин в проволочной спирали сопротивлением 15 Ом, если сила тока в спирали 2 А?
Решение: Q=I 2 Rt, нам все известно I=2А, R=15Ом, t=10мин=600с.
Q=2 2 ·15·600=36000 Дж = 36кДж.
Ответ: 36 кДж
Задание огэ по физике (фипи): Электрический паяльник включён в цепь напряжением 220 В. За 5 мин в нём выделилось количество теплоты 36,3 кДж. Чему равно сопротивление паяльника?
Задание огэ по физике (фипи): Две спирали электроплитки сопротивлением по 10 Ом каждая соединены последовательно и включены в сеть с напряжением 220 В. Через какое время на этой плитке закипит вода массой 1 кг, налитая в алюминиевую кастрюлю массой 300 г, если их начальная температура составляла 20 °С? Потерями энергии на нагревание окружающего воздуха пренебречь.
Задание огэ по физике: Сопротивление R1 первого кипятильника в 3 раза больше, чем сопротивление R2 второго кипятильника. При включении в одну и ту же сеть количество теплоты, выделяемое за единицу времени первым кипятильником, по сравнению со вторым
1) в 3 раза больше
2) в 3 резе меньше
3) в 9 раза больше
4) в 9 резе меньше
Решение: При включении в одну и ту же сеть по закону Ома сила тока у второго кипятильника больше так как сопротивление второго в три раза меньше, по закону Джоуля — Ленца Q=I 2 Rt, на первом резистре будет выделяться в три раза меньше тепла.
Ответ: 2.
Задание огэ по физике: Электрическая плитка при силе тока 6 А потребляет 1080 кДж энергии. Чему равно время прохождения тока по спирали плитки, если ее сопротивление 25 Ом?
1) 7200 с
2) 1200 с
3) 7,2 с
4) 1,2 с
Задание огэ по физике: Электрическая плитка, включена в сеть напряжением 220 В. Какую энергию потребляет плитка за 20 мин работы, если сила тока, протекающего через ее спираль, 5 А?
1) 22 кДж
2) 110 кДж
3) 1320 кДж
4) 4840 кДж
Решение: из закона Ома сначала найдем сопротивление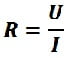 
, R=220/5=44 Ом, t = 20 мин = 1200 с, по закону Джоуля — Ленца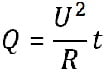 
Ответ: 3
Задание огэ по физике (фипи): Электрическая плитка при силе тока 6 А за 120 с потребляет 108 кДж энергии. Чему равно сопротивление спирали плитки?
Задание огэ по физике (фипи): Электрическая лампочка, включённая в сеть напряжением 220 В, за 30 мин потребляет 1980 кДж электроэнергии. Чему равна сила тока, протекающего через её спираль?
Задание огэ по физике (фипи): Сколько времени потребуется электрическому нагревателю, чтобы довести до кипения 2,2 кг воды, начальная температура которой 10 °С? Сила тока в нагревателе 7 А, напряжение в сети 220 В, КПД нагревателя равен 45%.
Решение: При протекании электрического тока через нагреватель выделяется энергия, которая идет на нагревание воды m=2,2 кг от температуры t1=10°С до t2=100°С, удельная теплоемкость воды с=4200 (Дж/кг·°С), из формулы для количества теплоты найдем Q1=cm1(t2-t1)= 4200·2,2(100-10)=831600 Дж — количество теплоты необходимое для нагревания воды.
Зная, что КПД нагревателя равен 45%, найдем сколько тепла выделяет электрический нагреватель Q=Q1/0,45=1848000 Дж.
Из формулы Q=IUt выразим время t=Q/(IU)=1848000/(7·220)=1200 c = 20 минут.
Ответ: 20 минут.
Задание демонстрационного варианта ОГЭ 2019: На рисунке изображена схема электрической цепи, состоящей из трёх резисторов и двух ключей К1 и К2. К точкам А и В приложено постоянное напряжение. Максимальное количество теплоты, выделяемое в цепи за 1 с, может быть получено,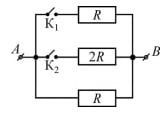 
1) если замкнут только ключ К1
2) если замкнут только ключ К2
3) если замкнуты оба ключа
4) если оба ключа разомкнуты
Решение: По закону Джоуля — Ленца 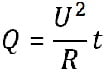, если напряжение постоянно, при уменьшении сопротивления, количество теплоты, выделяемое в цепи увеличивается. Следовательно, для того что бы количество теплоты выделяемое в цепи было максимально, необходимо уменьшить сопротивление цепи. При параллельном сопротивлении нескольких резисторов, их общее сопротивление меньше чем сопротивление отдельного резистора. Сопротивление будет минимальным при замыкании обоих ключей. Сопротивление будет минимальным, а количество теплоты выделяемое в цепи максимальным
Ответ: 3
Источник: fizikaege.com
Вычисление значений энтальпии, энтропии и энергии Гиббса химических реакций
Задача 55.
Вычислите изменение энтропии для химических процессов, протекающих по уравнениям:
a) 2NO(г) + O2(г) = 2NO2(г);
б) 2H2S(г) + 3O2(г) = 2SO2(г) + 2H2O(ж).
Решение:
Согласно 3-му следствию из закона Гесса, изменение энтропии химического процесса (ΔS°) определяется как разность сумм энтропий продуктов реакции и реагентов с учетом их стехиометрических коэффициентов в уравнении реакции. Расчет энтропии будем вести по формуле Гесса:
a) 2NO(г) + O2(г) = 2NO2(г)
Для этой реакции составaим уравнение расчета изменения энтропии в стандартных условиях:
По табличным данным установим значения энтропий (S°) участников процесса (Дж/моль·К):
Подставив найденные значения энтропий в искомое уравнение, и произведя расчеты, получим:
ΔS° = (2 · 240,2) – [(2 · 210,6) + 205,0] = -145,8 Дж/(моль·К).
Заметим при этом, что отрицательное значение изменения энтропии (убывание энтропии) свидетельствует о невозможности осуществления указанного процесса самопроизвольно в стандартных условиях.
б) 2H2S(г) + 3O2(г) = 2SO2(г) + 2H2O(ж).
Для этой реакции составим уравнение расчета изменения энтропии в стандартных условиях:
ΔS° = [2 · S0SO2(г) + 2 · S0H2O(ж)] – [2 · S0H2S(г) + 3S°O2(г)].
По табличным данным установим значения энтропий (S0) участников процесса (Дж/моль·К):
Подставив найденные значения энтропий в искомое уравнение, и произведя расчеты, получим:
ΔS° = [(2 · 248,1) + (2 . 70,1)] – [(2 · 205,7) + (3 · 205,0)] = -390,0 Дж/(моль·К).
Таким образом, отрицательное значение изменения энтропии (убывание энтропии) свидетельствует о невозможности осуществления указанного процесса самопроизвольно в стандартных условиях.
Вычисление энтальпии реакции
Задача 56.
Экспериментально установлено, что при взаимодействии 2,3 г натрия с водой выделяется 14,0 кДж теплоты. Вычислите энтальпию реакции.
Решение:
m(NaOH) = 2,3 г;
М(NaOH) = 46 г/моль;
Q = 14,0 кДж.
Уравнение реакции:
2,3 г 14,0 кДж
2Na + 2H2O = 2NaOH + H2; ΔH = ?
2* 43 г
Вычисляем энтальпию реакции из пропорции, получим:
2,3 г — 14,0 кДж
46 г —- х кДж
х = (46 . 14)/2,3 = 280 кДж.
ΔH = 280 кДж.
Можно проверить, используя табличные данные и следствие из закона Гесса, получим:
∆H°(Н2О) = -285,8 кДж;
∆H°(NaOH) = -425,6 кДж.
∆H° = [2∆H°(NaOH) — 2∆H°(Н2О)] = 2(-425,6) — 2(-285,8) = 280 кДж.
Задача 57.
1. Определить энтальпию образования CaHPO4(к), если термохимическое уравнение реакции имеет вид:
2Ca(OH)2(к) + P2O5(к) = 2CaHPO4(к) + H2O(г); ∆H = –1587 кДж.
Решение:
∆H°Cа(OН)2(к) = -985,1 кДж/моль;
∆H°Р2О5(к) = -1507,2 кДж/моль;
∆H°Н2О(г) = -241,81 кДж/моль;
∆H°CаНРО4(к) = ?
Согласно 2-му следствию из закона Гесса, изменение энтальпии химического процесса (ΔН°) определяется как разность сумм энттльпий продуктов реакции и реагентов с учетом их стехиометрических коэффициентов в уравнении реакции. Расчет энтальпии реакции получим:
Ответ: ∆H°CаНРО4(к) = -23713 кДж/моль.
Р.S. Слишком большое расхождение с табличными данными (-1808,6 кДж/моль) указывает на то, что ∆H° = –1587 кДж, указанное значение в условии задачи, иное (-381,6 кДж/моль).
Определение температуры наступления равновесия реакции
Задача 58.
При какой температуре наступит равновесие системы: CO(г) + 2H2(г) = CH3OH(ж)?
Решение:
∆H°CO(г) = -110,52 кДж/моль;
∆H°CH3OH(ж) = -238,9 кДж/моль;
S°(СО) = 197,55 Дж/моль . К;
S°(Н2) = 130,52 Дж/моль . К;
S°(СН3ОН) = 126,78 Дж/моль . К.
1. Находим ∆H°х.р. для данной системы.
Согласно 2-му следствию из закона Гесса, изменение энтропии химического процесса (ΔН°) определяется как разность сумм энтропий продуктов реакции и реагентов с учетом их стехиометрических коэффициентов в уравнении реакции. Расчет энтропии будем вести по формуле Гесса:
2. Находим ∆S°х.р. для данной системы
Согласно 3-му следствию из закона Гесса, изменение энтропии химического процесса (ΔS°) определяется как разность сумм энтропий продуктов реакции и реагентов с учетом их стехиометрических коэффициентов в уравнении реакции. Расчет энтропии будем вести по формуле Гесса:
∆S°х.р. = S°CH3OH — S°CO – S°H2;
∆S°х.р. = 129,78 – 197,55 – 130,52 =
= -331,81 Дж/(моль . К) = -0,33181 кДж/(моль . К).
3. Находим температуру равновесия системы
Для расчета температуры равновесия системы используем формулу: ∆G° = ∆H° — T∆S°.
В состоянии равновесия системы ∆G° = 0.
В этом случае — 0 = ∆H° — T∆S°.
Т = ∆H/∆S° = -128,38 кДж/моль/-0,33181 кДж/(моль . К) =
= 386,9 К.
Ответ: равновесие системы наступит при 386,9 К.
Определение направления химической реакции
Задача 59.
Дано уравнение: Fe2O3 + 2Al = Al2O3 + 2Fe. Вычислить тепловой эффект реакции, изменение стандартной энергии Гиббса при температуре 25 °С. В каком направлении будет протекать данная реакция?
Решение:
∆H°Fe2O3(к) = -822 кДж/моль;
∆H°Аl2O3(к) = -1675,7 кДж/моль;
S°Fe2O3(к) = 87 Дж/(моль . K);
S°Al2O3(к) = 50,9 Дж/(моль . K);
S°Fe(к) = 164,4 Дж/(моль . K);
S°Al(к) = 27,15 Дж/(моль . K).
2. Расчет энтропии реакции получим:
∆S°(х.р.)= ∑S°(обр.прод.) — ∑S°(обр.исх.);
∆S°(х.р.) = [S°Al2O3(к) + S°Fe(к)] — [S°Fe2O3(к) + S°Al(к)];
∆S°(х.р.) = (50,9 + 164,4) – (87 + 27,15) = 101,15 Дж/(моль·К) = 0,10115 Дж/(моль·К).
Переведем температуру из шкалы Цельсия в шкалу Кельвина: Т = 273 + 25 = 298 К. Для расчета ∆G°(298) воспользуемся уравнением:
∆G°(298) = ∆H° – T∆S°;
∆G°(298) = –853,7 – 298·(0,10115) = -883,8427 кДж.
Ответ: ∆Н(х.р.) = –853,7 кДж; ∆G°(298) = -883,8427 кДж.
Расчет энергии Гиббса реакции образования беспорядочного клубка лизин
Задача 60.
В отсутствии денатурирующих агентов константа равновесия Кр реакции образования беспорядочного клубка лизина при 298 К и рН = 7 равна 7,8. Рассчитать ∆G° 298 и оценить биологический аспект полученной величины.
Решение:
Рассчитаем ∆G°298 из формулы ∆G° = –RTlnK, получим:
∆rG°298 = –RTlnK = -[8,314 Дж/(моль . К) . 298 K . ln7,8] = -(8,314 . 298 .
ln7,8) = -(8,314 . 298 . 2,054) = -5089 Дж/моль.
Если ∆G° равно нулю (∆G° = 0), то реакция находится в равновесном состоянии.
Если ∆G° положительно (∆G° > 0), то реакция протекать самопроизвольно в прямом направлении не может. Однако обратная реакция идет самопроизвольно.
- Вы здесь:
- Главная
- Задачи
- Физическая химия
- Энтропия, энтальпия и энергия Гиббса реакций. Задачи 55 — 60
Источник: buzani.ru
Тепловые машины и второе начало термодинамики | теория по физике термодинамика
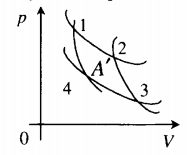
Определение Тепловые машины — устройства, в которых за счет внутренней энергии топлива совершается механическая работа. Чтобы тепловая машина работала циклически, необходимо, чтобы часть энергии, полученной от нагревателя, она отдавала холодильнику. Второе начало термодинамики В циклически действующем тепловом двигателе невозможно преобразовать все количество теплоты, полученное от нагревателя, в механическую работу. В тепловых машинах тепловые процессы замыкаются в цикле Карно. Так называют цикл, или идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов. В цикле Карно термодинамическая система выполняет механическую работу за счет обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. На графике цикл Карно представляется как две адиабаты и две изотермы:
- 1–2 — изотермическое расширение;
- 2–3 — адиабатное расширение;
- 3–4 — изотермическое сжатие;
- 4–1 — адиабатное сжатие.
КПД тепловой машины
Максимальный КПД соответствует циклу Карно.
Второе начало термодинамики
η = Q н − Q х Q н . . 100 % = Q н − P х t Q н . . 100 %
Преобразовывая формулу, получим:
η = A ‘ Q н . . 100 %
η = N t Q н . . 100 %
η = A ‘ A ‘ + Q х . . 100 %
η = T н − T х T н . . 100 %
- Qн (Дж) — количество теплоты, полученное от нагревателя (полученное количество теплоты);
- Qх (Дж) — количество теплоты, отданное холодильнику (отданное количество теплоты);
- A’ (Дж) — работа, совершенная газом;
- N (Вт) — полезная мощность;
- t (с) — время;
- Tн (К) — температура нагревателя;
- Tх (К) — температура холодильника.
Важно! Температуру следует выражать только в кельвинах (К) и КПД не бывает больше 100%.
Алгоритм решения задач на определение КПД теплового процесса
Рассмотрим решение на примере конкретной задачи:
На p-V-диаграмме изображен цикл, проводимый с одноатомным идеальным газом. Определите КПД этого цикла.
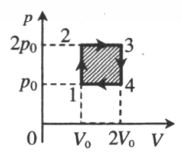
- Определить работу газа.
Если тепловой процесс представлен в осях (p, V), то можно определить работу, вычислив площадь фигуры, ограниченной замкнутым циклом:
Если тепловой процесс представлен в других осях координат, то сначала следует его перестроить в осях (p, V) и только потом определять работу.
- Выяснить, на каких этапах повышается температура газа. Именно здесь газ получает энергию:
1–2: V = const, давление увеличивается, температура увеличивается.
2–3: p = const, объем увеличивается, температура увеличивается.
3–4: V = const, давление понижается, температура понижается.
4–1: p = const, объем уменьшается, температура уменьшается.
Отсюда следует, что газ получает энергию только на первом и втором этапах.
- Определить с помощью первого начала термодинамики количество теплоты, полученное газом:
Q 12 = Δ U 12 = 3 2 . . Δ p V = 3 2 . . Δ p 0 V 0 = 1 , 5 p 0 V 0
Δ U 23 = Q 23 − A 23 ;
Δ U 23 = 3 2 . . Δ p V = 3 2 . . 2 Δ p 0 V 0 = 3 p 0 V 0
A 23 = p Δ V = 2 p 0 V 0
Q 23 = 3 p 0 V 0 + 2 p 0 V 0 = 5 p 0 V 0
Общее количество теплоты:
Q п о л у ч = Q 12 + Q 23 = 6 , 5 p 0 V 0
- Вычислить КПД, используя основную формулу:
η = A ‘ Q п о л у ч . . 100 %
η = p 0 V 0 6 , 5 p 0 V 0 . . 100 % = 15 , 4 %
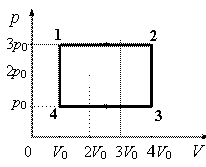
За цикл, показанный на рисунке, газ получает от нагревателя количество теплоты Qнагр = 5,1кДж. КПД цикла равен 4/17. Масса газа постоянна. На участке 1–2 газ совершает работу
Алгоритм решения
Источник: spadilo.ru