10 это какая дробь

В данной публикации мы рассмотрим, что из себя представляет десятичная дробь, как она пишется и читается, какой обыкновенной дроби соответствует и в чем заключается ее основное свойство. К теоретическому материалу прилагаются примеры для лучшего понимания.

Содержание скрыть

• Определение десятичной дроби
• Запись десятичной дроби
• Чтение десятичной дроби
• Основное свойство десятичной дроби

Определение десятичной дроби

Десятичная дробь – это особый вид записи обыкновенной дроби, знаменатель которой равен 10, 100, 1000, 10000 и т.д.

Такие дроби вместо привычного варианта написания ( с числителем, знаменателем и черточкой-разделителем), принято записывать так: 0,3 ; 2,6 ; 5,62 ; 7,238 и т.д.

Десятичные дроби бывают двух типов:

• конечные – после запятой конечное количество цифр;
• бесконечные – после запятой количество цифр бесконечно. Чаще всего такие дроби округляются до 1-3 цифр после запятой.

Запись десятичной дроби

Десятичная дробь состоит из целой и дробной частей, между которыми находится десятичный разделитель – в виде запятой или точки.

Десятичные дроби

Соответствие десятичной дроби обыкновенной:

• Целая часть (слева от запятой) аналогична той, что и при записи смешанных дробей (неправильную следует, также, переводить в смешанную). Если дробь правильная (числитель меньше знаменателя), то целая часть равна 0.
• Дробная часть (справа от запятой) содержит те же цифры, что и числитель дробной части, если бы мы представили дробь в виде обыкновенной.
• Количество цифр после запятой ограничено тем, на какое число делится числитель в обыкновенной дроби (количество цифр равно количеству нулей после единицы):

• 1 цифра – на 10;
• 2 цифры – на 100;
• 3 цифры – на 1000
• 4 цифры – на 10000;
• и т.д.

Примеры:

, т.к. после запятой одна цифра.

Источник: microexcel.ru

Перевод десятичной дроби в обыкновенную и наоборот: правило, примеры

Бывает, что для удобства расчетов нужно перевести обыкновенную дробь в десятичную и наоборот. О том, как это делать, мы поговорим в данной статье. Разберем правила перевода обыкновенных дробей в десятичные и обратно, а также приведем примеры.

Перевод обыкновенных дробей в десятичные

Мы будем рассматривать перевод обыкновенных дробей в десятичные, придерживаясь определенной последовательности. Во первых, рассмотрим, как в десятичные переводятся обыкновенные дроби со знаменателем, кратным 10: 10, 100, 1000 и т.д.Дроби с такими знаменателями, по сути, являются, более громоздкой записью десятичных дробей.

Далее мы рассмотрим, как переводить в десятичные дроби обыкновенные дроби с любым, не только кратным 10, знаменателем. Отметим, что при обращении обыкновенных дробей в десятичные получаются не только конечные десятичные, но и бесконечные периодические десятичные дроби.

Десятичные дроби, виды десятичных дробей, перевод десятичной дроби в обыкновенную и наоборот.

Перевод обыкновенных дробей со знаменателями 10, 100, 1000 и т.д. в десятичные дроби

Первым делом, скажем, что некоторые дроби нуждаются в определенной подготовке перед обращением в десятичный вид. В чем она заключается? Перед цифрой, стоящей в числителе, необходимо дописать столько нулей, чтобы количество цифр числителя стало равно числу нулей в знаменателе. Например, для дроби 3100 число 0 необходимо один раз дописать слева от 3 в числителе. Дробь 610, согласно изложенному выше правилу, не нуждается в доработке.

Рассмотрим еще один пример, после чего сформулируем правило, которым особенно удобно пользоваться на первых порах, пока опыта в обращении дробей не так много. Так, дробь 1610000 после дописывания нулей в числителе будет иметь вид 001510000.

Как перевести обыкновенную дробь со знаменателем 10, 100, 1000 и т.д. в десятичную?

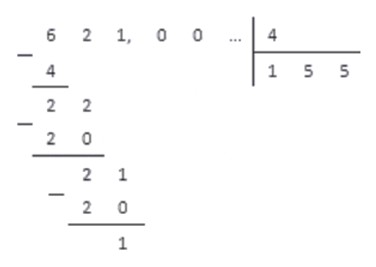
Рассмотрим решение еще одного примера, чтобы закрепить материал.

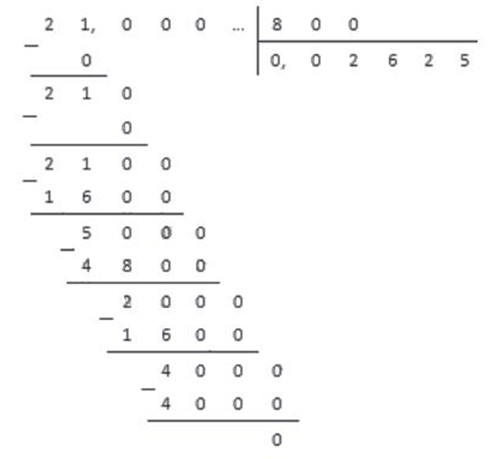
Но как быть, если при делении мы так и не получим в остатке 0. В таких случаях деление можно продолжать бесконечно долго. Однако, начиная с определенного шага, остатки будут периодически повторяться. Соответственно, будут повторяться и цифры в частном. Это значит, что обыкновенная дробь переводится в десятичную бесконечную периодическую дробь. Проиллюстрируем сказанное на примере.

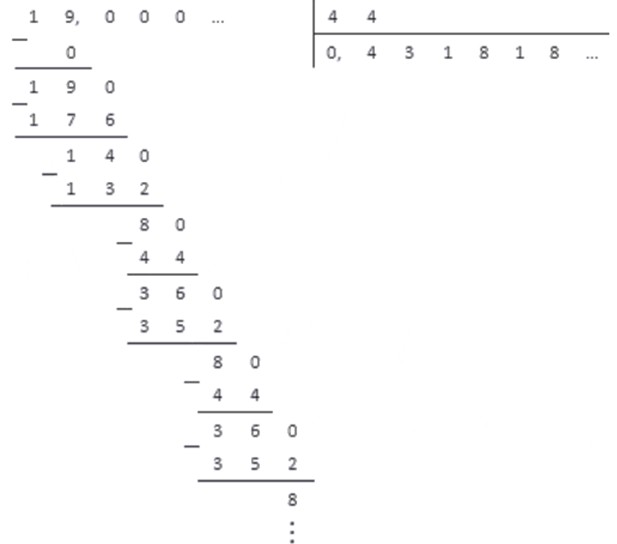
Пусть перед нами несократимая обыкновенная дробь. К какому виду она приведется? Какие обыкновенные дроби переводятся в конечные десятичные, а какие — в бесконечные периодические?

Во первых, скажем, что если дробь удается привести к одному из знаменателей 10, 100, 1000. то она будет иметь вид конечной десятичной дроби. Чтобы дробь приводилась к одному из таких знаменателей, ее знаменатель должен быть делителем хотя бы одного из чисел 10, 100, 1000 и т.д. Из правил разложения чисел на простые множители следует, что делитель чисел 10, 100, 1000 и т.д. должен, при разложении на простые множители, содержать лишь числа 2 и 5.

1. Обыкновенную дробь можно привести к виду конечной десятичной дроби, если ее знаменатель можно разложить на простые множители 2 и 5.
2. Если кроме чисел 2 и 5 в разложении знаменателя присутствуют другие простые числа, дробь приводится к виду бесконечной периодической десятичной дроби.

Пример 8. Перевод обыкновенных дробей в десятичные

Какая из данных дробей 47 20 , 7 12 , 21 56 , 31 17 переводится в конечную десятичную дробь, а какая — только в периодическую. Дадим ответ на этот вопрос, не выполняя непосредственно перевода обыкновенной дроби в десятичную.

Дробь 47 20 , как легко заметить, умножением числителя и знаменателя на 5 приводится к новому знаменателю 100 .

47 20 = 235 100 . Отсюда делаем вывод, что данная дробь переводится в конечную десятичную дробь.

Разложение знаменателя дроби 7 12 на множители дает 12 = 2 · 2 · 3 . Так как простой множитель 3 отличен от 2 и от 5 , данная дробь не может быть представлена в виде конечной десятичной дроби, а будет иметь вид бесконечной периодической дроби.

Дробь 21 56 , во-первых, нужно сократить. После сокращения на 7 получим несократимую дробь 3 8 , разложение знаменателя которой на множители дает 8 = 2 · 2 · 2 . Следовательно, это конечная десятичная дробь.

В случае с дробью 31 17 разложение знаменателя на множители представляет собой само простое число 17 . Соответственно, эту дробь можно обратить в бесконечную периодическую десятичную дробь.

Обыкновенную дробь нельзя перевести в бесконечную и непериодическую десятичную дробь

Выше мы говорили только о конечных и бесконечных периодических дробях. Но может ли какая-либо обыкновенная дробь быть обращена в вид бесконечной непериодической дроби?

При переводе бесконечной дроби в десятичную получается либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь.

Остаток от деления всегда меньше делителя. Другими словами, согласно теореме о делимости, если мы делим какое-то натуральное число на число q, то остаток деления в любом случае не может быть больше, чем q-1. После окончания деления возможна одна из следующих ситуаций:

1. Мы получаем в остатке 0, и на этом деление заканчивается.
2. Мы получаем остаток, который при последующем делении повторяется, в результате мы имеем бесконечную периодическую дробь.

Иных вариантов при обращении обыкновенной дроби в десятичную не может быть. Скажем также, что длина периода (количество цифр) в бесконечной периодической дроби всегда меньше, чем число цифр в знаменателе соответствующей обыкновенной дроби.

Перевод десятичных дробей в обыкновенные дроби

Теперь пришло время рассмотреть обратный процесс перевода десятичной дроби в обыкновенную. Сформулируем правило перевода, которое включает три этапа. Как перевести десятичную дробь в обыкновенную?

Правило перевода десятичных дробей в обыкновенные дроби

1. В числитель записываем число из исходной десятичной дроби, отбросив запятую и все нули слева, если они есть.
2. В знаменатель записываем единицу и за ней столько нулей, сколько цифр есть в исходной десятичной дроби после запятой.
3. При необходимости сокращаем полученную обыкновенную дробь.

Рассмотрим применение данного правила на примерах.

Пример 8. Перевод десятичных дробей в обыкновенные

Представим число 3 , 025 в виде обыкновенной дроби.

1. В числитель записываем саму десятичную дробь, отбросив запятую: 3025 .
2. В знаменателе пишем единицу, а после нее три нуля — именно столько цифр содержится в исходной дроби после запятой: 3025 1000 .
3. Полученную дробь 3025 1000 можно сократить на 25 , в результате чего мы получим: 3025 1000 = 121 40 .

Пример 9. Перевод десятичных дробей в обыкновенные

Переведем дробь 0 , 0017 из десятичных в обыкновенные.

1. В числителе запишем дробь 0 , 0017 , отбросив запятую и нули слева. Получится 17 .
2. В знаменатель записываем единицу, а после нее пишем четыре нуля: 17 10000 . Данная дробь несократима.

Если в десятичной дроби есть целая часть, то такую дробь можно сразу перевести в смешанное число. Как это сделать?

Сформулируем еще одно правило.

Правило перевода десятичных дробей в смешанные числа.

1. Число, стоящее в дроби до запятой, записываем как целая часть смешанного числа.
2. В числителе записываем число, стоящее в дроби после запятой, отбросив нули слева, если они есть.
3. В знаменателе дробной части дописываем единицу и столько нулей, сколько цифр есть в дробной части после запятой.

Обратимся к примеру

Пример 10. Перевод десятичной дроби в смешанное число

Представим дробь 155 , 06005 в виде смешанного числа.

1. Записываем число 155 , как целую часть.
2. В числителе записываем цифры после запятой, отбросив нуль.
3. В знаменателе записываем единицу и пять нулей

Поучаем смешанное число: 155 6005 100000

Дробную часть можно сократить на 5 . Сокращаем, и получаем финальный результат:

155 , 06005 = 155 1201 20000

Перевод бесконечных периодических десятичных дробей в обыкновенные дроби

Разберем на примерах, как осуществлять перевод периодических десятичных дробей в обыкновенные. Прежде чем начать, уточним: любую периодическую десятичную дробь можно перевести в обыкновенную.

Самый простой случай — период дроби равен нулю. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.

Пример 11. Перевод периодической десятичной дроби в обыкновенную

Обратим периодическую дробь 3 , 75 ( 0 ) .

Отбросив нули справа, получим конечную десятичную дробь 3 , 75 .

Обращая данную дробь в обыкновенную по алгоритму, разобранному в предыдущих пунктах, получаем:

3 , 75 ( 0 ) = 3 , 75 = 375 100 = 15 4 .

Как быть, если период дроби отличен от нуля? Периодическую часть следует рассматривать как сумму членов геометрический прогрессии, которая убывает. Поясним это на примере:

0 , ( 74 ) = 0 , 74 + 0 , 0074 + 0 , 000074 + 0 , 00000074 + . .

Для суммы членов бесконечной убывающей геометрической прогрессии существует формула. Если первый член прогрессии равен b , а знаменатель q таков, что 0 < q < 1 , то сумма равна b 1 — q .

Рассмотрим несколько примеров с применением данной формулы.

Пример 12. Перевод периодической десятичной дроби в обыкновенную

Пусть у нас есть периодическая дробь 0 , ( 8 ) и нам нужно перевести ее в обыкновенную.

0 , ( 8 ) = 0 , 8 + 0 , 08 + 0 , 008 + . .

Здесь мы имеем бесконечную убывающую геометрическую прогрессию с первым членом 0 , 8 и знаменателем 0 , 1 .

0 , ( 8 ) = 0 , 8 + 0 , 08 + 0 , 008 + . . = 0 , 8 1 — 0 , 1 = 0 , 8 0 , 9 = 8 9

Это и есть искомая обыкновенная дробь.

Для закрепления материала рассмотрим еще один пример.

Пример 13. Перевод периодической десятичной дроби в обыкновенную

Обратим дробь 0 , 43 ( 18 ) .

Сначала записываем дробь в виде бесконечной суммы:

0 , 43 ( 18 ) = 0 , 43 + ( 0 , 0018 + 0 , 000018 + 0 , 00000018 . . )

Рассмотрим слагаемые в скобках. Эту геометрическую прогрессию можно представить в следующем виде:

0 , 0018 + 0 , 000018 + 0 , 00000018 . . = 0 , 0018 1 — 0 , 01 = 0 , 0018 0 , 99 = 18 9900 .

Полученное прибавляем к конечной дроби 0 , 43 = 43 100 и получаем результат:

0 , 43 ( 18 ) = 43 100 + 18 9900

После сложения данных дробей и сокращения получим окончательный ответ:

0 , 43 ( 18 ) = 19 44

В завершение данной статьи скажем, что непериодические бесконечный десятичные дроби нельзя перевести в вид обыкновенных дробей.

Источник: zaochnik.com

2. Таблица разрядов

Десятичная дробь, как и любое число, состоит из цифр ( (0), (1), (2), (3), (4), (5), (6), (7), (8), (9) ).

Место каждой цифры в числе важно: оно определяет разряд числа.

Десятичная дробь состоит из целой части (все цифры до запятой) и дробной части (все цифры после запятой).

Целую часть десятичной дроби можно разбить на разряды так же, как и натуральные числа: единицы, десятки, сотни, тысячи и т. д.

Дробную часть десятичной дроби разбивают на разряды так:

десятые (в знаменателе обыкновенной дроби (10)), сотые (в знаменателе обыкновенной дроби (100)), тысячные (в знаменателе обыкновенной дроби (1000)) и т. д.

Таблица разрядов

Тысячи

Сотни

Десятки

Единицы ,

Десятые

Сотые

Тысячные

Десятитысячные

Таблицу разрядов можно дополнить любым нужным количеством столбцов.

(1)-й разряд после запятой — разряд десятых,
(2)-й разряд после запятой — разряд сотых,
(3)-й разряд после запятой — разряд тысячных,
(4) -й разряд после запятой — разряд десятитысячных,
(5)-й разряд после запятой — разряд стотысячных,
(6)-й разряд после запятой — разряд миллионных,
(7)-й разряд после запятой — разряд десятимиллионных,
(8)-й разряд после запятой — разряд стомиллионных.

Источник: www.yaklass.ru

Обращение десятичной дроби в обыкновенную

АЛГЕБРА

Автор Ольга Викторовна Опубликовано 25.06.2022

Как перевести десятичную дробь в обыкновенную? Чтобы из десятичной дроби сделать обыкновенную, достаточно в числителе дроби записать число, стоящее после запятой, а в знаменателе – единицу с нулями, причем нулей должно быть столько, сколько цифр справа от запятой (в дробной части десятичной дроби).

.

Это все равно, что записать десятичную дробь таким образом:

.

Примеры перевода дробей

Еще больше примеров как из десятичной дроби сделать обыкновенную. Давайте практиковаться:

• ,
• ,
• ,
• ,
• .

Зачем переводить десятичную дробь в обыкновенную

Для чего это нужно? Иногда в одном задании на нахождение значения выражения встречаются и обыкновенные и десятичные дроби. Поэтому бывает нужно сделать из десятичной дроби обыкновенную.

Например, необходимо найти значение выражения:

Можно перевести обыкновенную дробь в десятичную, или десятичную в обыкновенную, смотря какие нам даны дроби и как удобнее поступить.

.

Еще один пример. Найдите значение выражения:

.

Удобнее представить десятичные дроби в виде обыкновенных дробей:

Интересные статьи по алгебре:

• Обращение десятичной дроби в обыкновенную
• Десятичные дроби
• Геометрическая прогрессия
• Производная функции – определение и геометрический смысл
• Что такое множитель и разложение на простые множители
• Многочлены
• Одночлены
• Свойства степеней с натуральным показателем
• Производная корня
• Квадратный корень

Источник: repetitor-mathematics.ru